American Journal of Industrial and Business Management
Vol.1 No.1(2011), Article ID:8062,9 pages DOI:10.4236/ajibm.2011.11001
Dividend Payments and Related Problems in a Markov-Dependent Insurance Risk Model under Absolute Ruin
![]()
1School of Statistics and Mathematics, Shandong University of Finance and Economics, Jinan, China; 2Department of Mathematics and Physics, Shandong Jiaotong University, Jinan, China.
Email: yuwg@mail.sdu.edu.cn, yujuanh518@163.com
Received September 5th, 2011; revised September 19th, 2011; accepted September 29th, 2011.
Keywords: Absolute Ruin, Markov-Dependent Insurance Risk Model, Debit Interest, Moment-Generating Function
ABSTRACT
In this paper, we study the dividend payments prior to absolute ruin in a Markov-dependent risk process in which the claim occurrence and the claim amount are regulated by an external discrete time Markov chain. A system of integrodifferential equations with boundary conditions satisfied by the moment-generating function, the nth moment of the discounted dividend payments prior to absolute ruin and the discounted penalty function, given the initial environment state, are derived. In the two-state risk model, explicit solutions to the integro-differential equations satisfied by the nth moment of the discounted dividend payments prior to absolute ruin are obtained when the claim size distribution is exponentially distributed. Finally, the matrix form of systems of integro-differential equations satisfied by the discounted penalty function are presented.
1. Introduction
Recently ruin theory under regime-switching model is becoming a popular topic. This model is proposed in Reinhard [1] and Asmussen [2]. Asmussen [2] calls it a Markov-modulated risk model in which both the frequency of the claim arrivals and the distribution of the claim amounts are influenced by an external environment process. This model is a generalization of the classical compound Poisson risk model and the primary motivation for this generalization is the enhanced flexibility that it permits for the modeling of the claim arrival process and the claim severity distribution assumed in the classical risk process. The model builds a Markov chain whose states represent different states of an economy into the insurance risk model. The regime-switching of the states of the economy can be attributed to the structural changes in the (macro-) economic conditions, the changes in political regimes, the impact of (macro-) economic news and business cycles, etc. There are many papers published on ruin probabilities and the related problems under the Markov-modulated (or Markov regime-switching) risk model. Ng and Yang [3] give closed form solutions for the joint distribution of the surplus before and after ruin when the initial surplus is zero or when the claim amount distributions are phase-type distributed. Li and Lu [4] study the moments of the present value of the dividend payments and the distribution of the total dividends prior to ruin for the Markov-modulated risk model modified by the introduction of a barrier dividend. Lu and Li [5] and Liu et al. [6] consider a regime-switching risk model with a threshold dividend strategy. Zhu and Yang [7] study a more general Markovian regimeswitching risk model in which the premium, the claim intensity, the claim amount, the dividend payment rate and the dividend threshold level are influenced by an external Markovian environment process. Wei et al. [8] consider the Markov-modulated insurance risk model with tax.
Moreover, in recent years, semi-Markovian risk model has attracted attention in the literature. Albrecher and Boxma [9] study the expected discounted penalty function in a semi-Markovian dependent risk model in which at each instant of a claim, the underlying Markov chain jumps to a new state and the distribution of claim depends on this state. Liu et al. [10,11] consider the expected discounted penalty function under the constant dividend barrier and dividends payments under the threshold strategy in a Markov-dependent risk model, respectively. They consider the structure of a semiMarkovian dependence type as follows. Let 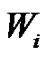 denote the time between the arrival of the
denote the time between the arrival of the 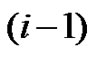 th and the ith claims and
th and the ith claims and 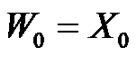 a.s., then
a.s., then

where 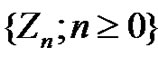 is an irreducible discrete time Markov chain with state space
is an irreducible discrete time Markov chain with state space 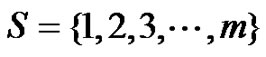 and transition matrix
and transition matrix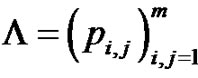 ,
,  is the amount of the nth claim.
is the amount of the nth claim.
Thus at each instant of a claim, the Markov chain jumps to a state j and the distribution  of the claim depends on the new state j, and has a positive mean
of the claim depends on the new state j, and has a positive mean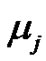 . Then, the next interarrival time is exponentially distributed with parameter
. Then, the next interarrival time is exponentially distributed with parameter . Note that given the states
. Note that given the states  and
and , the quantities
, the quantities 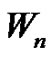 and
and 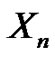 are independent, but there is an autocorrelation among consecutive claim sizes and among consecutive interclaim times as well as crosscorrelation between
are independent, but there is an autocorrelation among consecutive claim sizes and among consecutive interclaim times as well as crosscorrelation between 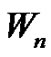 and
and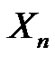 .
.
Inspired by Albrecher and Boxma [9] and Liu et al. [10,11], in this paper we propose to generalize the semiMarkovian risk model to the absolute ruin risk model. In the new risk model, we assume that the insurer could borrow an amount of money equal to the deficit at a debit interest force  when the surplus is negative. Meanwhile, the insurer will repay the debts continuously from his/her premium income. When the negative surplus attains the level
when the surplus is negative. Meanwhile, the insurer will repay the debts continuously from his/her premium income. When the negative surplus attains the level  or is below
or is below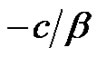 , the surplus is no longer able to be positive. Absolute ruin occurs at this moment. Moreover, when the surplus exceeds the constant barrier
, the surplus is no longer able to be positive. Absolute ruin occurs at this moment. Moreover, when the surplus exceeds the constant barrier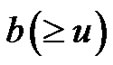 , dividends are paid continuously so the surplus stays at the level b until a new claim occurs. Some recent references about absolute ruin risk model include Zhou and Zhang [12], Cai [13], Gerber and Yang [14], Yuen et al. [15], Yuan and Hu [16],Wang and Yin [17], Ming et al. [18], Wang et al. [19], Zhang et al. [20], Yu and Huang [21] and references therein.
, dividends are paid continuously so the surplus stays at the level b until a new claim occurs. Some recent references about absolute ruin risk model include Zhou and Zhang [12], Cai [13], Gerber and Yang [14], Yuen et al. [15], Yuan and Hu [16],Wang and Yin [17], Ming et al. [18], Wang et al. [19], Zhang et al. [20], Yu and Huang [21] and references therein.
The surplus process 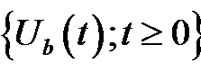 under the Markovdependent risk model is given by
under the Markovdependent risk model is given by
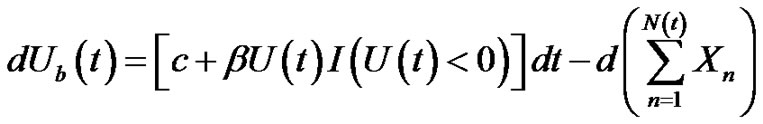
where 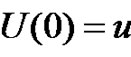 is the initial surplus, c the premium rate,
is the initial surplus, c the premium rate, 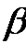 the debit interest,
the debit interest, 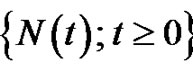 the number of claims up to time t, and
the number of claims up to time t, and 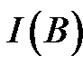 means the indicator function of an event B. Furthermore, we assume the net profit condition holds, that is
means the indicator function of an event B. Furthermore, we assume the net profit condition holds, that is
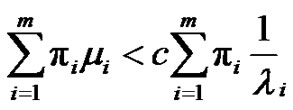
where 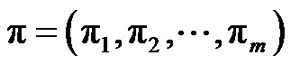 is the stationary distribution of process
is the stationary distribution of process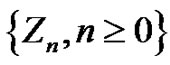 .
.
Let 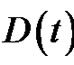 be the cumulative amount of dividends paid out up to time t and
be the cumulative amount of dividends paid out up to time t and  the force of interest, then
the force of interest, then
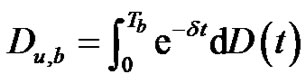
is the present value of all dividends until time of ruin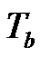 , where
, where 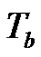 denoted by
denoted by 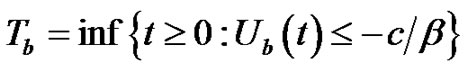 is the time of absolute ruin.
is the time of absolute ruin.
In the sequel we will be interested in the momentgenerating function
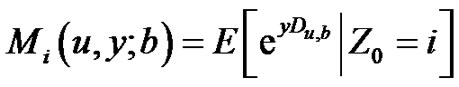 ,
, 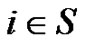
and the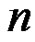 th moment function
th moment function
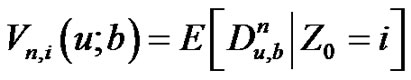 ,
, 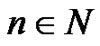 ,
, 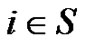
with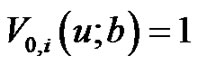 , and the expected discounted penalty function, for
, and the expected discounted penalty function, for 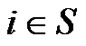
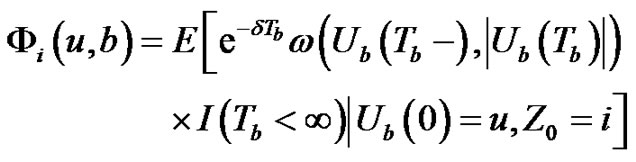
where, 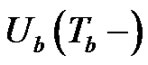 is the surplus prior to absolute ruin and
is the surplus prior to absolute ruin and  is the deficit at absolute ruin. The penalty function
is the deficit at absolute ruin. The penalty function 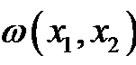 is an arbitrary nonnegative measurable function defined on
is an arbitrary nonnegative measurable function defined on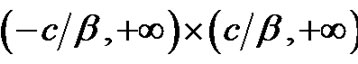 . Throughout this paper we assume that
. Throughout this paper we assume that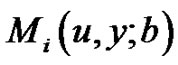 ,
, 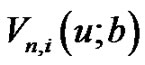 and
and 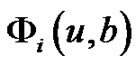 are sufficiently smooth functions in u and y, respectively.
are sufficiently smooth functions in u and y, respectively.
Then, fix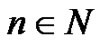 , the expected present value of the total dividend payments until ruin in the stationary case is given by
, the expected present value of the total dividend payments until ruin in the stationary case is given by
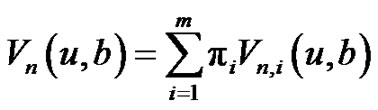
The rest of the paper is organized as follows. In Sections 2, we get integro-differential equations for the moment-generating function and boundary conditions in a Markov-dependent risk model. In section 3, the integro-differential equations satisfied by higher moment of the dividend payments and boundary conditions are derived. Examples for a two-state risk model are illustrated in section 4 when the claim size distribution is exponentially distributed. In the last section, we obtain the systems of integro-differential equations for the discounted penalty function and its matrix form.
2. Moment-Generating Function of Du,b
In this section, we discuss the integro-differential equations satisfied by the moment-generating function at absolute ruin. We point out that  has different paths for
has different paths for 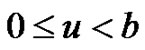 and
and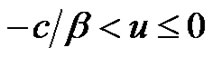 . For
. For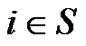 , we define
, we define
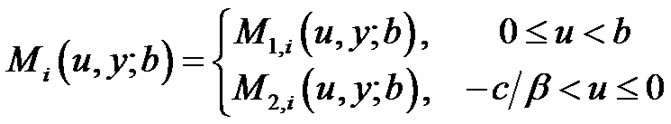
Theorem 2.1 For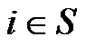 ,
, 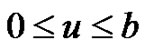 , we have
, we have
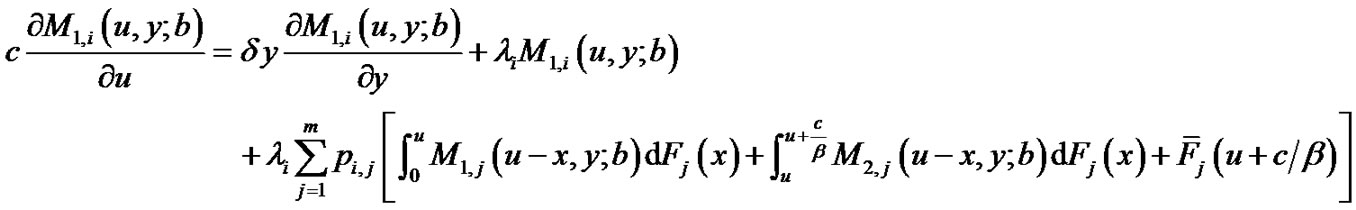 (2.1)
(2.1)
and, for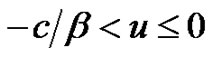 ,
,
 (2.2)
(2.2)
with boundary conditions, for ,
,
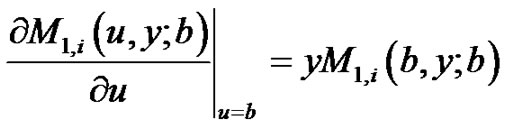 (2.3)
(2.3)
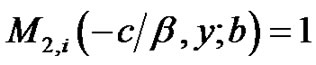 (2.4)
(2.4)
where,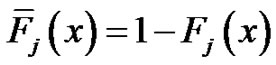 .
.
Proof. Fix , and
, and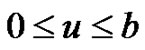 . Considering a small time interval
. Considering a small time interval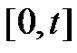 , such that
, such that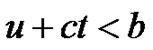 . In view of the strong Markov property of the surplus process
. In view of the strong Markov property of the surplus process 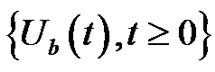 , we have
, we have
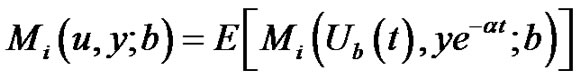 (2.5)
(2.5)
Conditioning on the event occurring in the interval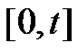 , we obtain
, we obtain
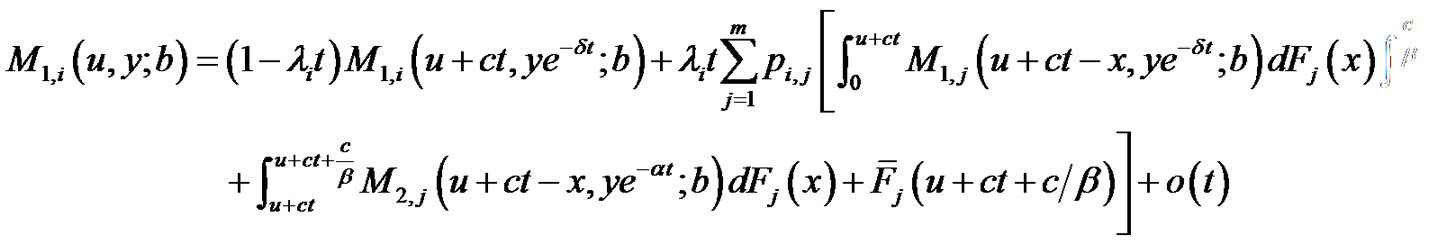 (2.6)
(2.6)
Taylor’s expansion gives
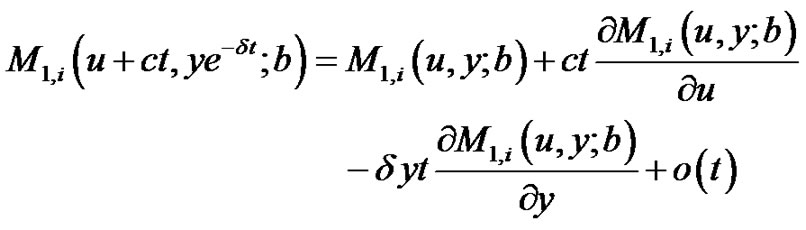 (2.7)
(2.7)
Substituting (2.7) into (2.6), dividing both sides by t, and letting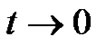 , we obtain (2.1).
, we obtain (2.1).
Similarly, when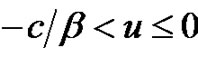 , we still consider a small time interval
, we still consider a small time interval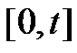 , with
, with 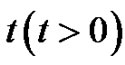 being sufficiently small so that the surplus will not reach 0 in the time interval. Let
being sufficiently small so that the surplus will not reach 0 in the time interval. Let 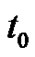 be the solution to
be the solution to
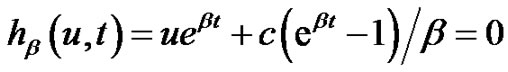
Then 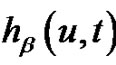 is the surplus at time
is the surplus at time 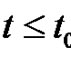 if no claim occurs prior to time
if no claim occurs prior to time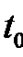 . We assume
. We assume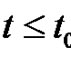 . So conditioning on the time and the amount of the first claim, we have
. So conditioning on the time and the amount of the first claim, we have
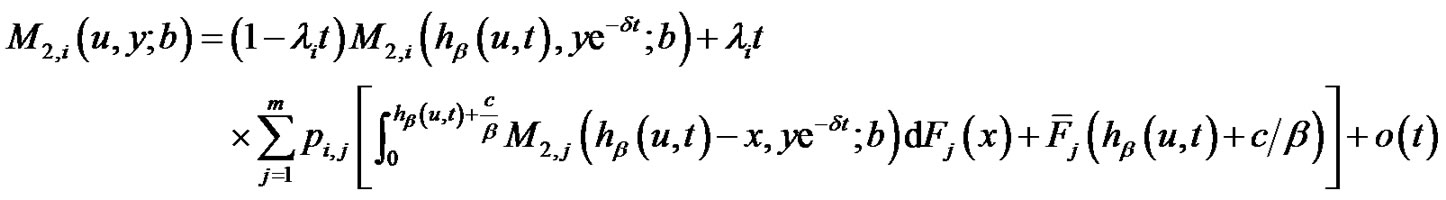 (2.8)
(2.8)
By Taylor’s expansion
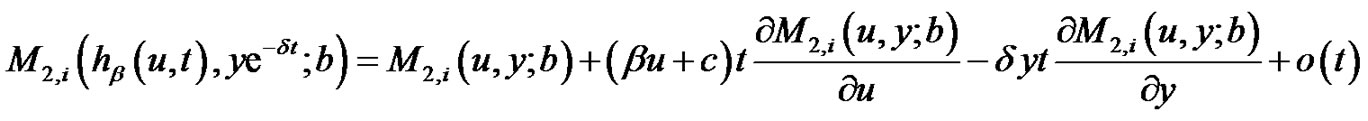 (2.9)
(2.9)
Substituting (2.9) into (2.8), dividing both sides by t, and letting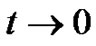 , we obtain (2.2).
, we obtain (2.2).
When the initial surplus is b, we obtain
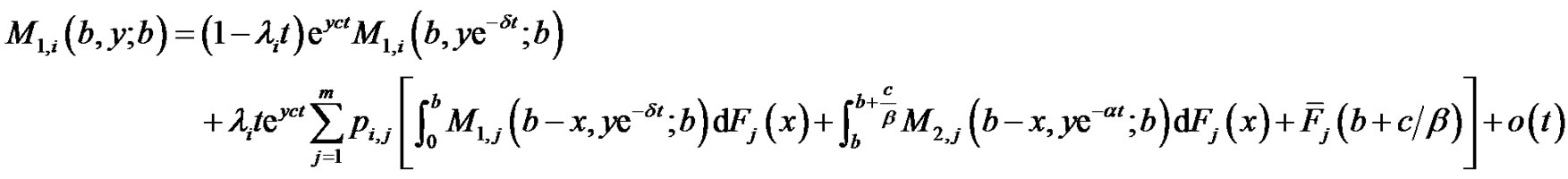 (2.10)
(2.10)
Using Taylor’s expansion, we have,
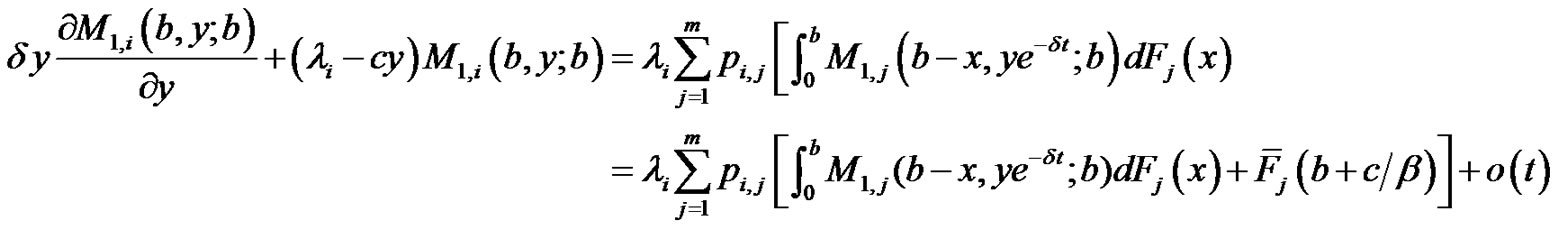 (2.11)
(2.11)
Letting 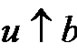 in (2.1) and comparing it with (2.11), we obtain (2.3). Where “
in (2.1) and comparing it with (2.11), we obtain (2.3). Where “ ” denoting increasing approach.
” denoting increasing approach.
When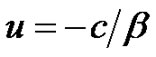 , absolute ruin is immediate. Thus, no dividend is paid. So we obtain (2.4). Theorem 2.1 is proved.
, absolute ruin is immediate. Thus, no dividend is paid. So we obtain (2.4). Theorem 2.1 is proved.
Theorem 2.2 For ,
,
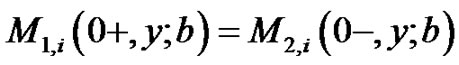 (2.12)
(2.12)
Proof. For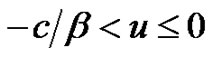 , letting
, letting 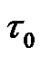 be the time that the surplus reach 0 for the first time from
be the time that the surplus reach 0 for the first time from 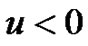 and using the Markov property of the surplus process, we obtain
and using the Markov property of the surplus process, we obtain
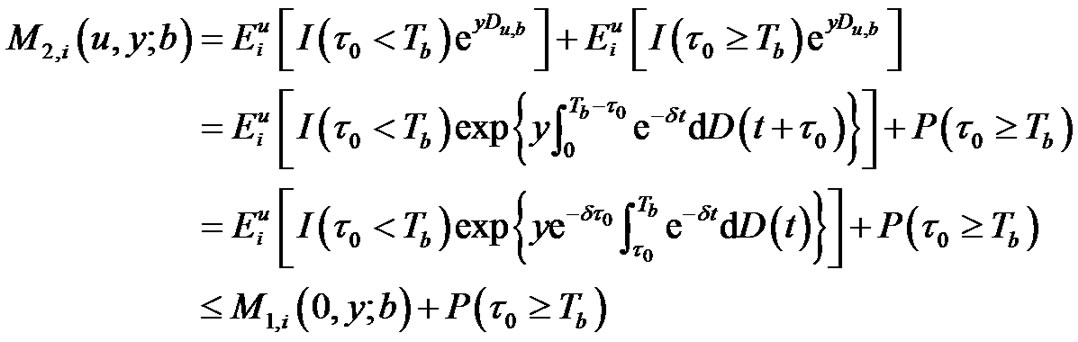 (2.13)
(2.13)
Similarly, we obtain
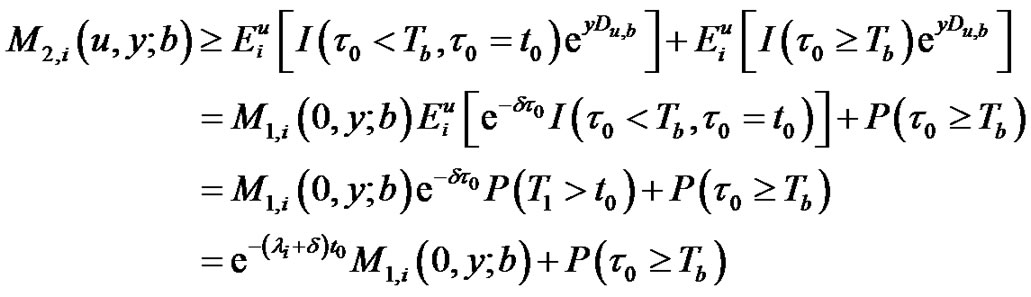 (2.14)
(2.14)
where 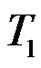 is the time of the first claim.
is the time of the first claim.
When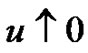 , we notice that
, we notice that  and
and 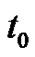 both go into zero. Letting
both go into zero. Letting 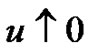 in (2.13) and (2.14) and in view of
in (2.13) and (2.14) and in view of
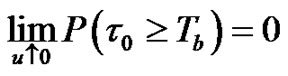
we obtain (2.12). Theorem 2.2 is proved.
3. Higher Moment of the Dividend Payments
We now derive a system of integro-differential equations satisfied by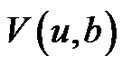 . By the definitions of
. By the definitions of 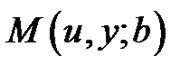 and
and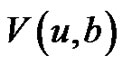 , we obtain, for
, we obtain, for ,
,
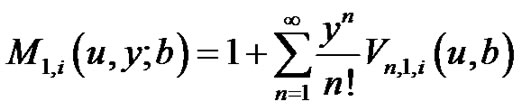 (3.1)
(3.1)
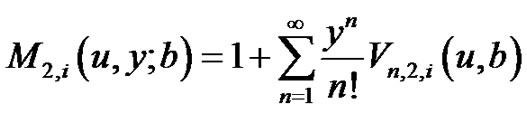 (3.2)
(3.2)
where, 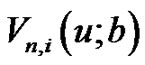 is defined by
is defined by
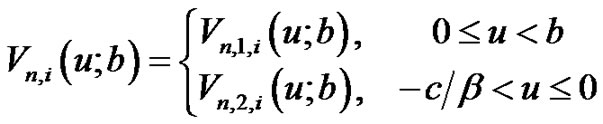
Substituting (3.1) and (3.2) into (2.1) and (2.2), respectively, and comparing the coefficients of 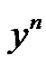 yield the following integro-differential equations:
yield the following integro-differential equations:
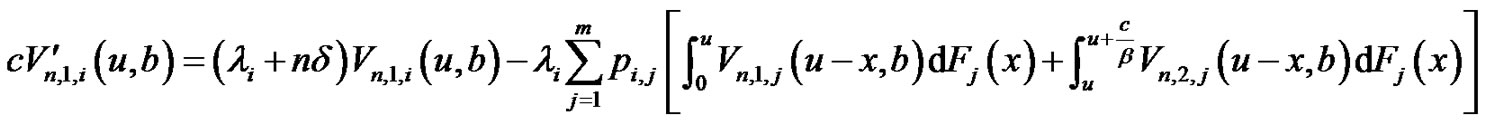 (3.3)
(3.3)
for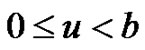 , and for
, and for ,
,
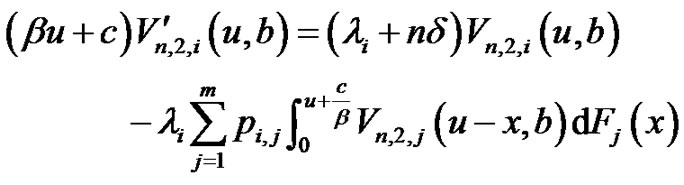 (3.4)
(3.4)
Substituting (3.1) into (2.3), similarly, we obtain
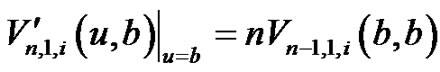 (3.5)
(3.5)
Thus, 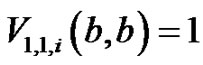 is an obvious result since
is an obvious result since 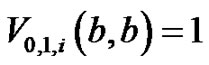 .
.
Substituting (3.1) and (3.2) into (2.4) and (2.12), we obtain, for 
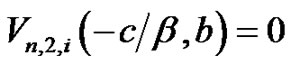 (3.6)
(3.6)
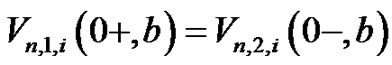 (3.7)
(3.7)
Letting 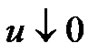 in (3.3) and
in (3.3) and 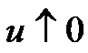 in (3.4) and using (3.7), we obtain, for
in (3.4) and using (3.7), we obtain, for .
.
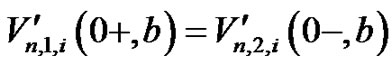 (3.8)
(3.8)
where, “ ” denoting decreasing approach.
” denoting decreasing approach.
4. Explicit Expressions for Exponential Claims to 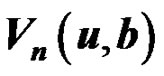 for a Two-State Model
for a Two-State Model
In this section, we consider a two-state Markov-dependent risk model. Then 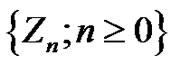 is a two-state Markov chain, which reflects the random environmental effects due to “normal” vs. “abnormal”, or “high season” vs. “low season” conditions. We derive the explicit formulae for
is a two-state Markov chain, which reflects the random environmental effects due to “normal” vs. “abnormal”, or “high season” vs. “low season” conditions. We derive the explicit formulae for 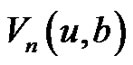 when the claim size is exponentially dis tributed
when the claim size is exponentially dis tributed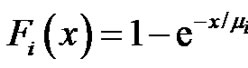 ,
,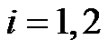 . Set
. Set ,
,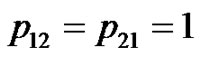 . In view of Equation (3.3) and the expo nential density function, Equation (3.3) are reduced to, for
. In view of Equation (3.3) and the expo nential density function, Equation (3.3) are reduced to, for 
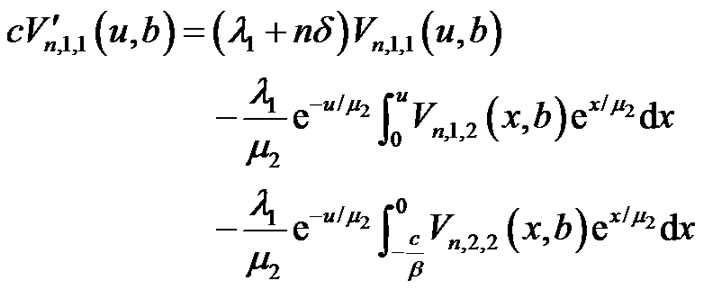 (4.1)
(4.1)
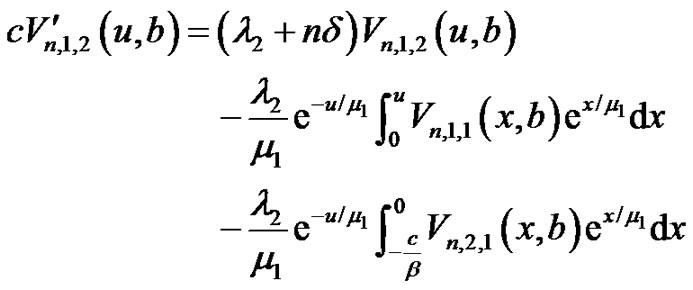 (4.2)
(4.2)
Applying the operator 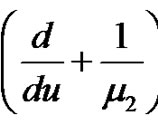 and
and  on
on
(4.1) and (4.2), respectively, and rearranging them, we obtain, for 
 (4.3)
(4.3)
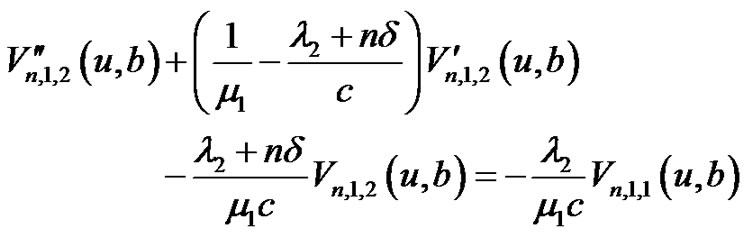 (4.4)
(4.4)
They are second-order linear non-homogeneous differential equations with constant coefficients. For convenient writing, let
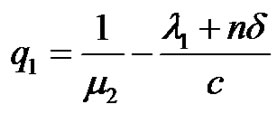 ,
, 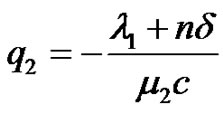
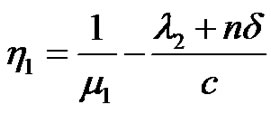 ,
, 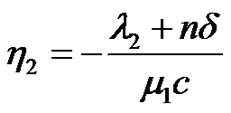
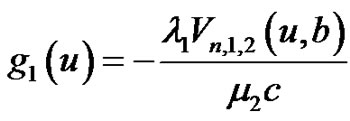 ,
, 
Then Equation (4.3) and Equation (4.4) can be rewriteten as
 (4.5)
(4.5)
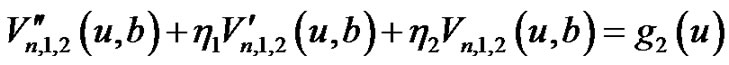 (4.6)
(4.6)
The corresponding homogeneous differential Equations of (4.5) and (4.6) are
 (4.7)
(4.7)
 (4.8)
(4.8)
The general solutions of Equations (4.7) and (4.8) are
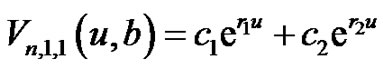 (4.9)
(4.9)
 (4.10)
(4.10)
where ,
, 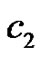 ,
, 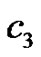 ,
, 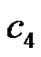 are arbitrary constants,
are arbitrary constants,
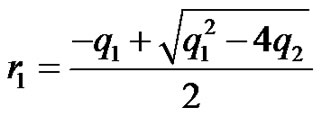

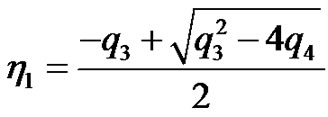
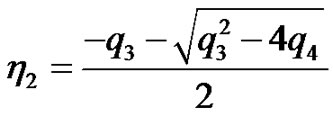
According to the variation of constants method, we assume 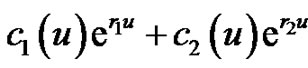 and
and 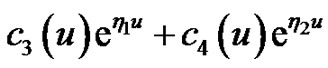 are special solutions of Equations (4.5) and (4.6), respectively. Then we have
are special solutions of Equations (4.5) and (4.6), respectively. Then we have
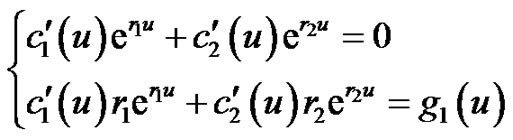 (4.11)
(4.11)
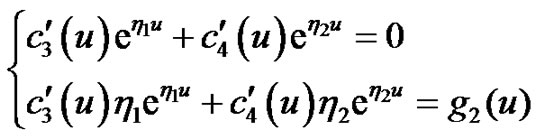 (4.12)
(4.12)
Solving the above two equations, we obtain


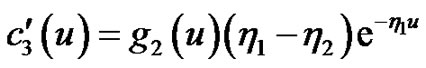
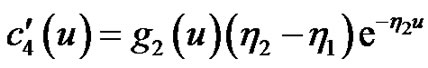
then we have, for 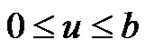
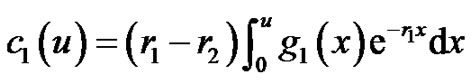
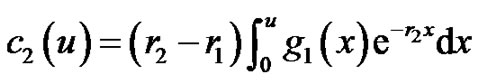
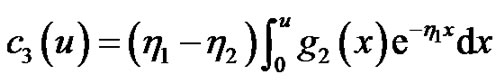
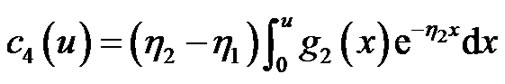
So the general solutions of Equations (4.5) and (4.6) are, for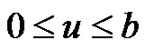 ,
,
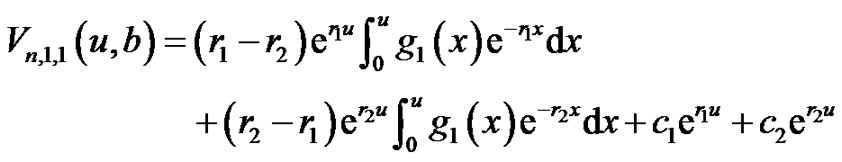 (4.13)
(4.13)
 (4.14)
(4.14)
5. The Discounted Penalty Function
In this section, we derive integro-differential equations for the discounted penalty functions. For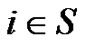 , define
, define
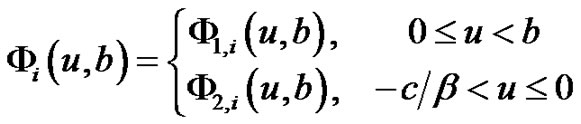
Note that in the stationary case, we have
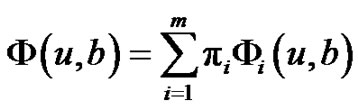
Theorem 5.1 For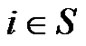 ,
, 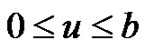 ,
,
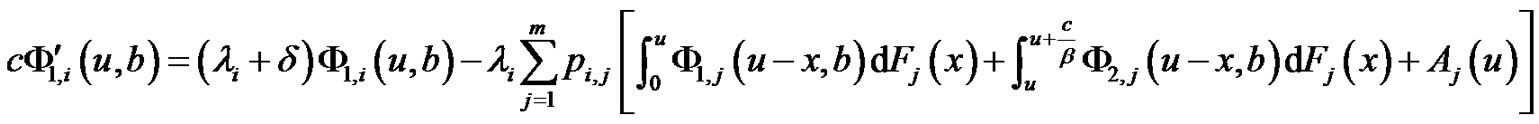 (5.1)
(5.1)
and, for ,
,
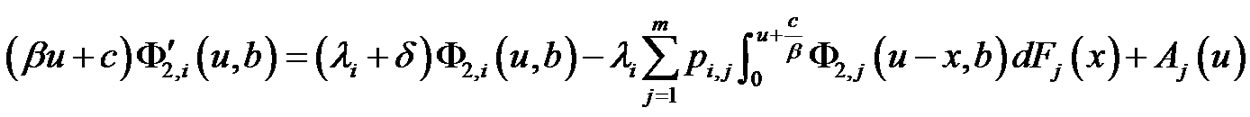 (5.2)
(5.2)
with boundary conditions
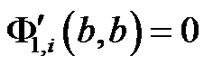 (5.3)
(5.3)
 (5.4)
(5.4)
 (5.5)
(5.5)
where

Proof. For  and
and . Similar to argument as in Section 2, we condition on the events that can occur in the small time interval
. Similar to argument as in Section 2, we condition on the events that can occur in the small time interval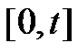 .
.
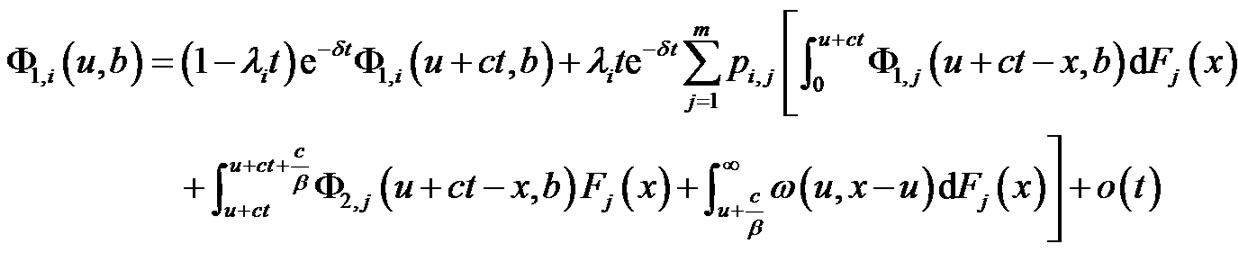 (5.6)
(5.6)
Since
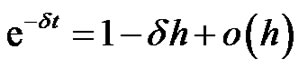
we then get
 (5.7)
(5.7)
Equation (5.7) can be rewritten as
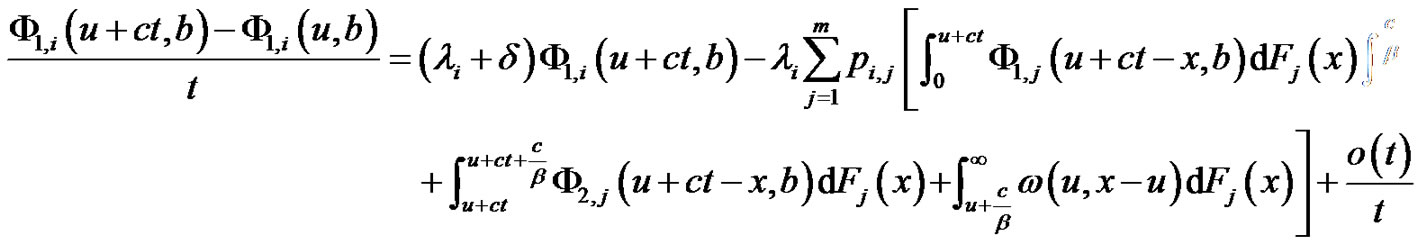 (5.8)
(5.8)
Letting 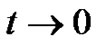 in (5.8), we obtain (5.1).
in (5.8), we obtain (5.1).
For 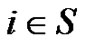 and
and , we have
, we have
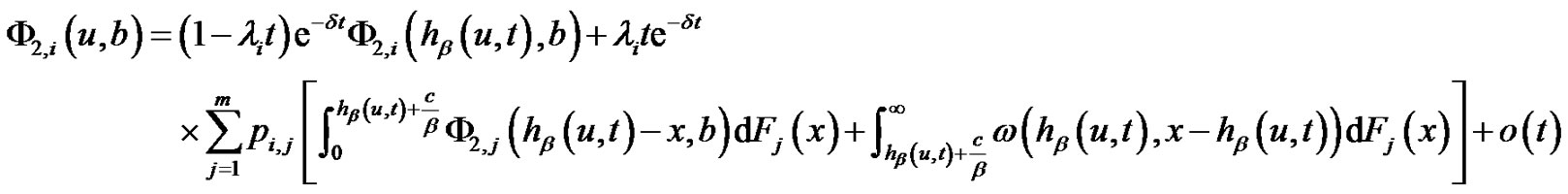 (5.9)
(5.9)
By Taylor’s expansion
 (5.10)
(5.10)
Substituting (5.10) into (5.9), dividing both sides by t, and letting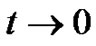 , we obtain (5.2). Theorem 5.1 is proved.
, we obtain (5.2). Theorem 5.1 is proved.
Integro-differential Equations (5.1) and (5.2) can eas ily be rewritten in matrix form.
Let
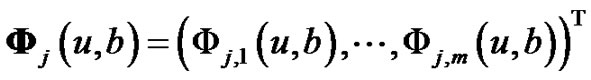 ,
,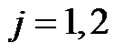 .
.
“T” denoting transpose. Rewritten (5.1) and (5.2) in matrix, then we have Theorem 5.2 The integro-differential equation in ma trix form for 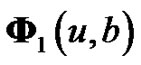 and
and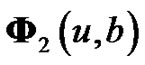 , for
, for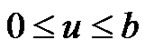 ,
,
 (5.11)
(5.11)
and, for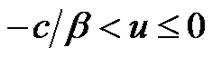 ,
,
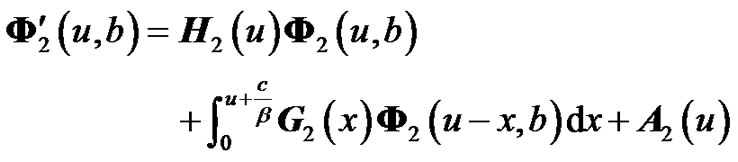 (5.12)
(5.12)
where

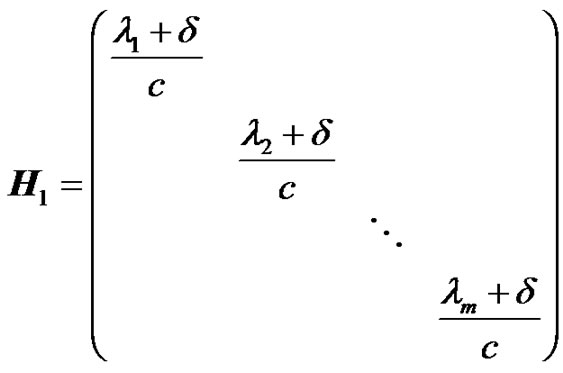
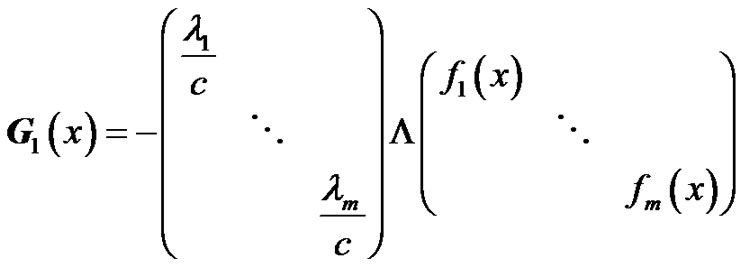
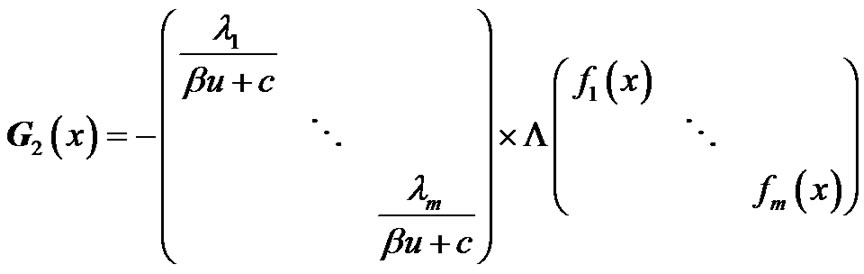
are all  matrices, and
matrices, and 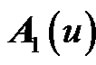 and
and 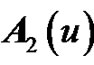 defined by
defined by

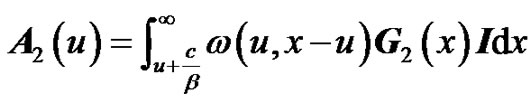
are all m-dimensional vector, in which 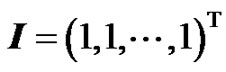 is an
is an 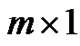 column vector. The continuity condition and derivative condition for
column vector. The continuity condition and derivative condition for 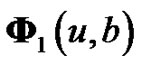 and
and 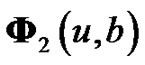 is
is
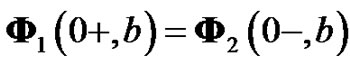 ,
,
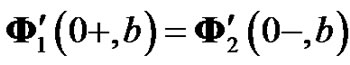 .
.
6. Acknowledgements
The authors are very grateful to the editor and two anonymous referees for their valuable comments and suggestions which led to the present improved version of the manuscript. This research was supported by Humanities and Social Sciences Project of the Ministry Education of China (No. 09YJC910004; No. 10YJC630092) and Shandong Provincial Natural Science Foundation of China (No. ZR2010GL013) and Research Program of Higher Education of Shandong Province (No. J10WF84) and Natural Science Foundation of Shandong Jiaotong University (No. Z201031).
REFERENCES
- J. M. Reinhard, “On a Class of Semi-Markov Risk Models Obtained as Classical Risk Models in a Markovian Enviroment,” Astin Bulletin, Vol. 14, 1984, pp. 23-43.
- S. Asmussen, “Risk Theory in a Markovian Environment,” Scandinavian Actuarial Journal, No. 2, 1989, pp. 69- 100.
- A. Ng and H. Yang, “On the Joint Distribution of Surplus Prior and Immediately after Ruin under a Markovian Regime Switching Model,” Stochastic Processes and Their Applications, Vol. 116, No. 2, 2006, pp. 244-266. doi:10.1016/j.spa.2005.09.008
- S. M. Li and Y. Lu, “Moments of the Dividend Payments and Related Problems in a Markov-Modulated Risk Model,” North American Actuarial Journal, Vol. 11, No. 2, 2007, pp. 65-76.
- Y. Lu and S. Li, “The Markovian Regime-Switching Risk Model with a Threshold Dividend Strategy,” Insurance: Mathematics and Economics, Vol. 44, No. 2, 2009, pp. 296-303. doi:10.1016/j.insmatheco.2008.04.004
- J. Liu, J. C. Xu and H. C. Hu, “The Markov-Dependent Risk Model with a Threshold Dividend Strategy,” Wuhan University Journal of Natural Sciences, Vol. 16, No. 3, 2011, pp. 193-198. doi:10.1007/s11859-011-0736-9
- J. Zhu and H. Yang, “Ruin Theory for a Markov Regime-Switching Model under a Threshold Dividend Strategy,” Insurance: Mathematics and Economics, Vol. 42, No. 1, 2008, pp. 311-318. doi:10.1016/j.insmatheco.2007.03.004
- J. Q. Wei, H. L. Yang and R. M. Wang, “On the Markovmodulated Insurance Risk Model with Tax,” Blaetter der DGVFM, Vol. 31, No. 1, 2010, pp. 65-78. doi:10.1007/s11857-010-0104-4
- H. Albrecher and O. Boxma, “On the Discounted Penalty Function in a Markov-Dependent Risk Model,” Insurance Mathematics and Economics, Vol. 37, No. 2, 2005, pp. 650-672. doi:10.1016/j.insmatheco.2005.06.007
- J. Liu, J. C. Xu and Y. J. Hu, “On the Expected Discounted Penalty Function in a Markov-Dependent Risk Model with Constant Dividend Barrier,” Acta Mathematica Scientia, Vol. 30B, No. 5, 2010, pp. 1481-1491.
- J. Liu, J. C. Xu and H. C. Hu, “Dividend Payments with a Threshold Strategy in a Markov-Dependent Risk Model,” Wuhan University Journal of Natural Sciences, Vol. 16, No. 1, 2011, pp. 11-15. doi:10.1007/s11859-011-0703-5
- M. Zhou and C. Zhang, “Absolute Ruin under Classical Risk Model,” Acta Mathematicae Applicate Sinica, Vol. 28, No. 4, 2005, pp. 57-80.
- J. Cai, “On the Time Value of Absolute Ruin with Debit Interest,” Advances in Applied Probability, Vol. 39, No. 2, 2007, pp. 343-359. doi:10.1239/aap/1183667614
- H. U. Gerber and H. L. Yang, “Absolute Ruin Probabilities in a Jump Diffusion Risk Model with Investment,” North American Actuarial Journal, Vol. 11, No. 3, 2007, pp. 159-169.
- K. C. Yuen, M. Zhou and J. Y. Guo, “On a Risk Model with Debit Interest and Dividend Payments,” Statistics and Probability Letters, Vol. 78, No. 15, 2008, pp. 2426-2432. doi:10.1016/j.spl.2008.02.021
- H. L. Yuan and Y. J. Hu, “Absolute Ruin in the Compound Poisson Risk Model with Constant Dividend Barrier,” Statistics and Probability Letter, Vol. 78, No. 14, 2008, pp. 2086-2094. doi:10.1016/j.spl.2008.01.076
- C. W. Wang and C. C. Yin, “Dividend Payments in the Classical Risk Model under Absolute Ruin with Debit Interest,” Applied Stochastic Models in Business and Industry, Vol. 25, No. 3, 2009, pp. 247-262. doi:10.1002/ asmb.722
- R. X. Ming, W. Y. Wang and L. Q. Xiao, “On the Time Value of Absolute Ruin with Tax,” Insurance: Mathematics and Economics, Vol. 46, No. 1, 2010, pp. 67-84. doi:10.1016/j.insmatheco.2009.09.004
- C. W. Wang, C. C. Yin and E. Q. Li, “On the Classical Risk Model with Credit and Debit Interests under Absolute Ruin,” Statistics and Probability Letters, Vol. 80, No. 15, 2010, pp. 427-436. doi:10.1016/j.spl.2009.11.020
- Z. M. Zhang, H. L. Yang and H. Yang, “On the Absolute Ruin in a Map Risk Model with Debit Interest,” Advances in Applied Probability, Vol. 43, No. 1, 2011, pp. 77-96. doi:10.1239/aap/1300198513
- W. G. Yu and Y. J. Huang, “Absolute Ruin for a Risk Model with Credit and Debit Interest under a Threshold Dividend Strategy,” Far East Journal of Applied Mathematics, Vol. 57, No. 2, 2011, pp. 125-137.

