Open Journal of Orthopedics
Vol.07 No.03(2017), Article ID:75196,11 pages
10.4236/ojo.2017.73010
Human Gait Kinematic Measurement
Samaniego L. José María, Castillo C. Pablo
Vempto S.P.A., Santiago, Chile
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 20, 2017; Accepted: March 28, 2017; Published: March 31, 2017
ABSTRACT
This study presents the measurement of the angular position and acceleration during the leg gait and the data fitting using Fourier series to parameterize the measurements obtained through accelerometers. The sensor reference is the gravity direction for the three axes that is converted into angular position and acceleration data. For this study, measurements were made in the femoral area of a human leg. The curves were obtained based on Fourier series, and though a homologation made to their harmonics, we obtained ordinary differential equations (ODEs) that parameterize these curves. The curves were approximated using six harmonics, resulting in six ODEs. The summed solutions of the ODEs represent the angular position or inclination of the leg during a walk step. The first and second derivative of the ODEs means the velocity and the acceleration of the leg movement. These types of tools are required in different research subjects such as health, entertainment, and engineering.
Keywords:
Human Gait, Kinematic, Fourier Series, Accelerometer

1. Introduction
The kinematics that the human gait considerably changes between different people and between two steps of the same person. To study, understand, compare and use the bipedal gait of the human body is necessary to quantify the leg movement during walk steps, including the forces involved on the kinematics, and it is important to know the forces involved. This paper proposes, through using accelerometers, a method of measuring and parameterizing the position and acceleration of human gaits for medical purposes.
Although there are studies that show the principles and phases present in the walk of a person [1] [2] [3] [4] , it is affected in every person by numerous factors, including health [5] [6] , age [7] [8] [9] , the physical state [10] , and gender [11] . Being able to measure and quantify the variables involved in the movements of the human body is justified in three main research categories [12] : physiology and health, computational, and robotics. From the physiological and health perspective, the area for which this work was conceived allows us to develop prostheses or orthoses to offer better rehabilitation in amputated patients or persons with walks disorders [7] [13] [14] , to study the progress of certain pathological diseases in the walk [15] [16] , and to prevent injuries and optimize athletes during their activities [17] [18] . The area of computing allows us, for example, to create animations based on human movements, while these studies are used in robotics to make robots and bipedal exoskeletons for different purposes [19] .
Several methods are currently used for the recognition and analysis of human gaits, and they can be classified into three classes: (i) image processing, (ii) force platforms, and (iii) wearable sensors [16] [17] [18] [19] [20] . In general, the first two have the same problems in being computationally and economically expensive, and they often require a sophisticated clinical laboratory [21] [22] . On the other hand, wearable sensors, e.g., accelerometers (such as those used in this work), have the following advantages without losing precision in the measurement: they are small and inexpensive, have low-computational cost, are easy to adjust, and can perform measurements in any environment [23] - [28] .
A code is programmed in this work that can read the data measured by the accelerometer, represent dimensionless acceleration values, translate them in terms of angular position or the inclination of the segment measured after processing, and calculate the actual acceleration of these in the sagittal plane or the side plane. These kinematics data are intended to be parameterized with differential equations.
2. Methodology
This section explains the general procedure to obtain data from acceleration, sensors used, operation, and calibrations to translate the reference values into representative values in this report. The mathematical model that consists of an approximation using Fourier series and a homologation to obtain ordinary differential equations (ODEs) from the approach is shown. Finally, the expected structure of the results is described.
For this work, a random person was selected and measured, whose specific characteristics are presented in the results section.
Figure 1 shows the position in the femoral zone where the sensor was located.
Figure 2 shows how the angular position in the sagittal (a) and the coronal (b) planes are measured in biomechanics [3] .
2.1. Measurements and Data Processing
The leg movement is measured using sensors. The sensors have 3 axis accelerometers (x, y, and z) and the selected measurement frequency is 100 Hz. Each sensor can take up to 900 measurements at one measurement cycle. The accelerometers can sense the direction of gravity, delivering a unique combination of. the three directions for each position [27] [28] .
Figure 1. Accelerometer position.
Figure 2. References systems for angular position in sagital plane (a), and in coronal plane (b).
The measured information is received in the computer in a particular format. These measurements, referential and dimensionless, have two types of errors, noise in the signal and an error in the output value; the errors are corrected through the code as follows.
The noise produced during walking due to the movement and impacts of the foot with the ground are eliminated using a low-pass filter, as these phenomena are of high frequency. A Gaussian filter is created in the frequency spectrum using the fast Fourier transform and its inverse [29] [30] .
For instabilities in the internal structure of the apparatus and changes in temperature, blows, or other components, the output presents a unique and unknown error for each device, which is called the BIAS error. If it is integrated twice to find the position values, as is often done mathematically, it will increase considerably. To avoid this, another calibration system is used, as is described below.
2.2. Calibration
A database was generated from measurements made on strategic positions. This database considers inclinations between 40˚ and 40˚ in the coronal plane and from 90˚ to 90˚ in the sagittal plane. The database was also considered for both planes with a gap of 10˚ between each measurement. These ranges were selected because they are above the maximum values of a passive bipedal walk.
The calibration curves were generated using the database, and by using these curves, the code interpolated each data point by delivering the angular position values to the sagittal and coronal plane.
For measurements in the sagittal plane of the segment, the data was already filtered and normalized by an acceleration of 2.932 × 10−2 [m/s2].
With the data of angular positions and acceleration obtained, it is possible to begin the parameterization of the data.
2.3. Mathematical Model
A segment (step) of the measurement was selected on which the model would be applied. With the objective to formulate a model, it was not essential to choose the segment to study rigorously, since the code operates in the same way regardless of the segment chosen. In this study, we chose to select a complete random step that was determined by the peaks observed in the measurements before being filtered.
Since these are periodic and continuous movements, Fourier series fitting was used to fit the selected step. The structure of the Fourier series is similar to the solution of certain differential equations, and a fit is generated to obtain ODEs that describe the kinematics variables sought from the measured signals. The two steps of the current model are explained in more detail as follows.
2.3.1. Fourier Series Fitting
Since any continuous and periodic function can be described by a sum of sines and cosines with certain arguments and amplitude constants [31] [32] , we used Fourier series to present the structure as shown in (1).
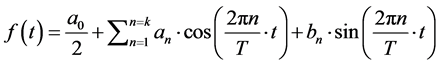 (1)
(1)
Equation (1) highlights the sum of trigonometric functions with equal arguments known as harmonics. As the number of harmonics increases, or for higher values of k in the series, the approximation is expected to be more accurate. Equation (2) shows the structure of the n-harmonic.
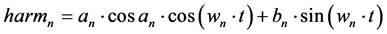 (2)
(2)
Each harmonic, n, corresponds to a sum of one sine and one cosine multiplied by amplitude constant, an and bn, respectively. Additionally, they are unique for each harmonic, and with an argument, wn・t, they are also unique for each harmonic but equal for both functions. This argument has the value of the independent variable, t, which corresponds in our case to time and the value wn, which represents something similar to the frequency of the harmonic, which is given by (3).
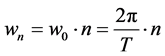 (3)
(3)
where:
・ T, period of function, or the time that the full cycle of the selected step takes.
・ n, harmonic number.
・ w0, frequency of the function, or selected step, determined by T.
The different values of the frequency of each harmonic are multiples. The frequency of the first harmonic, w0, and they increase as the value of n increases. It is expected that a greater harmonic lowers the incidence in the overall behavior of the approximation.
Figure 3 exposes the behavior of the series and the effect of increasing the number of harmonics present in the series.
The figure also shows an approximation with 1, 3, 7, and 15 harmonics to the function (4):
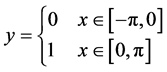 (4)
(4)
2.3.2. Homologation with Ordinary Differential Equations
ODEs are those in which a dependent variable―in this case, the angular position―interacts with one or more of its derivatives with respect to the independent variable, t. There is a second-order type of ODE, shown in (5), that has been intensively studied mathematically and has a known solution [33] [34] .
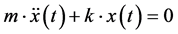 (5)
(5)
where
・ 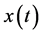 represents angular position of the leg as a function of time;
represents angular position of the leg as a function of time;
Figure 3. Approximation by Fourier series.
・ k represents the stiffness constant; and
・  represents the second derivative of the dependent variable with respect to the time, which the second derivative corresponds to acceleration in this case.
represents the second derivative of the dependent variable with respect to the time, which the second derivative corresponds to acceleration in this case.
These equations have associated initial position and velocity conditions and and
and 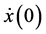 that are determined by the constant values k and m.
that are determined by the constant values k and m.
The solution to this ODE is presented in (6) and corresponds to the angular position of the leg, in the position measured, as a function of time
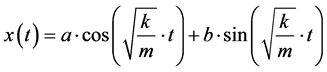 (6)
(6)
The structure of these solutions is similar to that presented by each harmonic, so it is possible to find, or associate, each harmonic of the series of an ODE. Additionally, a periodic representation of the selected step can be obtained from a sum of the solutions of these ODEs.
A relation of the constants k and m of the equations that parameterize the variables is useful for manufacturing Prostheses. It normalizes the value of the constant k so that it is always equal to 1 and only varies the value of m.
The amplitude constants for each solution, a and b, are equal to the respective amplitude constants for each harmonic n, which means 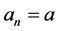 and
and 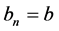 for each n. The constant m is determined by the relation shown in (7), which is obtained after equalizing the arguments of each harmonic with those of the solution of the corresponding ODE.
for each n. The constant m is determined by the relation shown in (7), which is obtained after equalizing the arguments of each harmonic with those of the solution of the corresponding ODE.
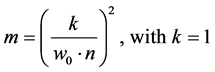 (7)
(7)
The values obtained of the constants k and m for the ODE model were defined. The sum of the solutions represents the curve of the angular position for the selected step and forms a continuous and periodic function as it is repeated. Lastly, the sum of the second derivative of these solutions corresponds to the acceleration curve.
3. Results
This section shows the results obtained in the femoral area of a subject. Table 1 shows the characteristics of the person and the conditions under which the measurements were made.
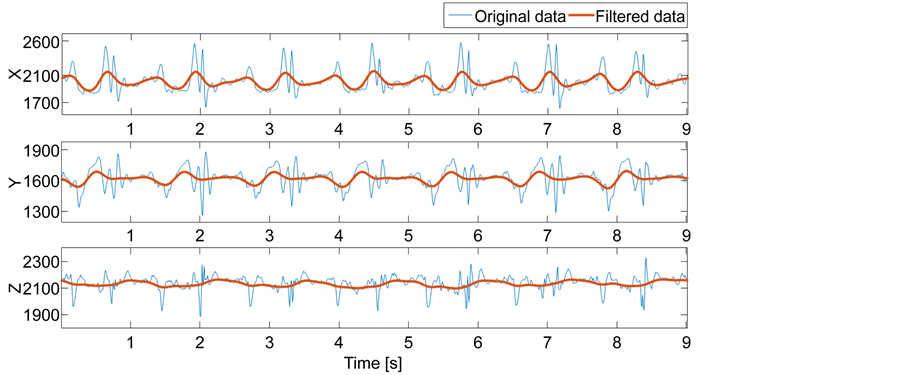
Figure 4 shows three graphics, one for each axis. Each one presents a curve with the original measurement of referential acceleration and another with the filtered data.
In the original data, a series of alterations is seen along the whole signal. It is possible to distinguish areas where there are peaks with greater amplitude that correspond to the moment when the foot impacts with the floor. As for the filter created, it creates a curve that follows the overall behavior of the measurements, eliminating the noise and delivering a more continuous and smooth curve.
Table 1. Characteristics from measured person and gait conditions.
Figure 4. Original and filtered referential data, femoral section.
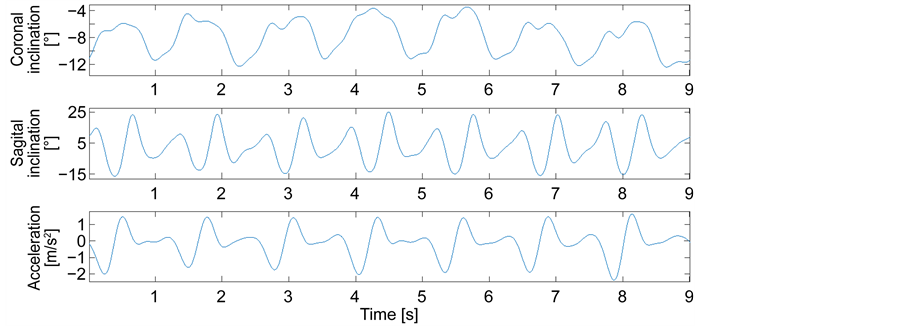
Figure 5 presents the data already translated using the calibration. The first and second graphs provide the inclinations of the segment along the measurement in the coronal and sagittal plane, respectively. The third graph shows the actual acceleration of the zone recorder by the sensor. Figure 6 shows the same results, but a step on the walk is selected.
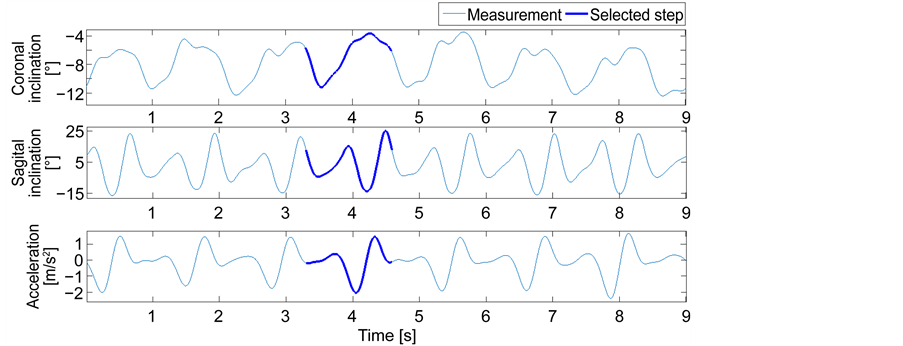
Figure 6 shows how a certain step on walk (corresponding to each step measured) is repeated on time. It is possible to determine that they are not the same, because they have slight differences between them.
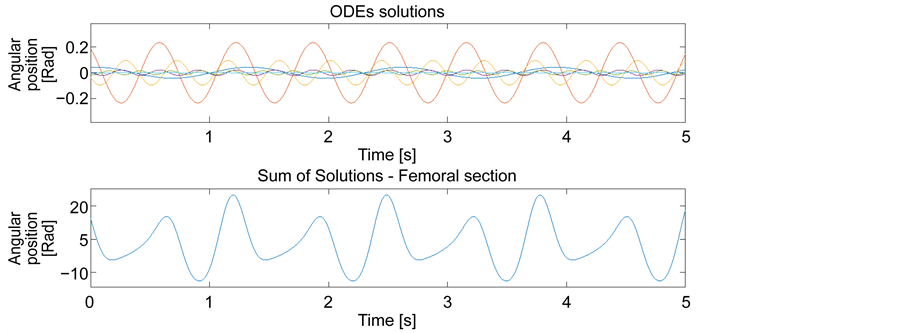
Figure 7 presents two graphs. The first corresponds to the solution of each ODE found for the sagittal position. It requires six harmonics to make an approximation with a quadratic error of 1.7 × 10−4. The second graph corresponds to the sum of these solutions.
Figure 7 shows that it is possible to successfully recognize that Fourier approximation allows a conversion to an equal number of ODEs. This also recreates the step measured periodically over time. These results could be used to construct elements such as prostheses, exoskeletons, or bipedal robots, which reproduce these curves.
Figure 5. Angular position and acceleration, femoral zone.
Figure 6. Selected step.
Figure 7. ODEs and the sum of them.
The table contains the fitted values of the mass constant and initial conditions of the ODEs.
The desired parameterization is achieved using values of Table 2.
The results obtained correspond to measurements in the femoral area of a person; in this work, measurements have also been made satisfactorily in the tibial area (the segment located between the heel and the knee).
Table 2. ODE fitted values.
4. Conclusions
A model is developed to parameterize kinematic, angular position, and acceleration data of the different areas of a person’s leg. This is done using three-axis accelerometers. Accurate data are obtained and is consistent with the film taken during the measurement.
The parameterization was performed, presenting considerably low-quadratic errors (1.7 × 10−4) through a sum of the solutions of second order ODEs.
A direct application of this study is the possibility to do kinematic measurements at low cost and in any place to obtain accurate and parameterized data. This allows the analysis of the progression in diseases, elaborate mechanisms that help in the rehabilitation of patients, and robotic motions or animations of bipedal walking.
The main limitation of the work is the calibration. Although making the calibration accurate within the ranges expected for people walking is easy, it can be even more accurate (with more reference points and greater accuracy in the inclination of the sensors for the measurements for the database), and the calibration ranges can be expanded to perform measurements in other types; for example, in arms.
Acknowledgements
We would like to thank ATTOELECTRONICS SPA for designing, manufacturing, and programming the sensors to measure the accelerations.
Cite this paper
María, S.L.J. and Pablo, C.C. (2017) Human Gait Kinematic Measurement. Open Journal of Orthopedics, 7, 79-89. https://doi.org/10.4236/ojo.2017.73010
References
- 1. Vaughan, C., Davis, B. and O’Connor, J. (1999) Dynamics of Human Gait. Kiboho Publishers, Cape Town.
- 2. Racic, V., Pavic, A. and Brownjohn, J. (2009) Experimental Identification and Analytical Modeling of Human Walking Forces: Literature Review. Journal of Sound and Vibration, 326, 1-49.
- 3. Sanchez-Lacuesta, J. (1992) Biomechanics of Normal and Pathological Human Gait. Instituto de Biomecánica de Valencia, Valencia.
- 4. Perry, J. and Burnfield, J. (1992) Gait Analysis: Normal and Pathological Function. SLACK Incorporated, New Jersey.
- 5. Haro, M. (2014) Laboratory of Gait and Movement. Revista Médica Clinica las Condes, 25, 237-247.
- 6. Sutherland, D. (2005) The Evolution of Clinical Gait Analysis Part III—Kinetics and Energy Assessment. Gait & Posture, 21, 447-461.
https://doi.org/10.1016/j.gaitpost.2004.07.008 - 7. Feng, J., Wick, J., Bompiani, E. and Aiona, M. (2016) Application of Gait Analysis in Pedriatic Orthopaedics. Current Orthopedic Practice, 27, 25-34.
- 8. Gu, K.H. and Dingwell, J. (2008) Separating the Effects of Age and Walking Speed on Gait Variability. Gait & Posture, 27, 572-577.
https://doi.org/10.1016/j.gaitpost.2007.07.009 - 9. Seunguk, K., Shari, L., Winters, J. and Ferrucci, L. (2009) Age-Related Mechanical Work Expenditure During Normal Walking. Journal of Biomechanics, 42, 1834-1839.
https://doi.org/10.1016/j.jbiomech.2009.05.037 - 10. Lai, P., Leung, A., Li, A. and Zhang, M. (2008) Three-Dimensional Gait Analysis of Obese Adults. Clinical Biomechanics, 23, S2-S6.
https://doi.org/10.1016/j.clinbiomech.2008.02.004 - 11. Chang, P.C., Tien, M.C., Wu, J.L. and Hu, C.S. (2009) Real-Time Gender Classification from Human Arbitrary View Angles. IEEE International Symposium on Multimedia, San Diego, 14-16 December 2009, 88-95.
- 12. Contreras, L.E., Tristancho, J.A. and Vargas, L.F. (2012) Biomechanical Analysis of Human Gait Trough Modelling Techniques. Entre Ciencia e Ingeniería, 6, 29-35.
- 13. Sun, J. (2015) Dynamic Modeling of Human Gait Using a Model Predictive Control Approach. Dissertations, Marquette University, Wisconsin.
- 14. Schiehlen, W. and García-Vallejo, D. (2011) Walking Dynamics from Mechanism Models to Parameter Optimization. Human Body Dynamics, 2, 199-211.
- 15. Whittle, M.W. (1996) Clinical Gait Analysis: A Review. Human Movement Science, 15, 369-387.
- 16. Tao, W.J., Liu, T., Zheng, R.C. and Feng, H.T. (2012) Gait Analysis Using Wearable Sensors. Sensors, 12, 2255-2283.
https://doi.org/10.3390/s120202255 - 17. Gouwanda, D. and Senanayake, S.M.N.A. (2008) Emerging Trends of Body-Mounted Sensors in Sports and Human Gait Analysis. In: Osman, N.A.A., Ibrahim, F., Abas, W.A.B.W., Rahman, H.S.A. and Ting, H.-N., Eds., 4th Kuala Lumpur International Conference on Biomedical Engineering 2008, Vol. 21, Springer, Berlin Heidelberg, 715-718.
https://doi.org/10.1007/978-3-540-69139-6_178 - 18. Gabel, M., Gilad-Bachrach, R., Renshaw, E. and Schuster, A. (2012) Full Body Gait Analysis with Kinect. 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, 28 August-1 September 2012, 1964-1967.
- 19. Azevedo, C., Andreff, N. and Arias, S. (2004) Bipedal Walking: From Gait Design to Experimental Analysis. Mechatronics, 14, 639-665.
- 20. Muro-de-la-Herran, A., García-Zapirain, B. and Méndez-Zorrilla, A. (2014) Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors, 14, 3362-3394.
https://doi.org/10.3390/s140203362 - 21. Sutherland, D.H. (2002) The Evolution of Clinical Gait Analysis. Part II: Kinematics. Gait & Posture, 16, 159-179.
https://doi.org/10.1016/S0966-6362(02)00004-8 - 22. Dixon, P.C., Böhm, H. and Döderlein, L. (2012) Ankle and Midfoot Kinetics during Normal Gait: A Multi-Segment Approach. Journal of Biomechanics, 45, 1011-1016.
https://doi.org/10.1016/j.jbiomech.2012.01.001 - 23. Öberg, T., Karsznia, A. and Öberg, K. (1994) Joint Angle Parameters in Gait: Reference Data for Normal Subjects, 10 - 79 Years of Age. Journal of Rehabilitation Research and Development, 31, 199-213.
- 24. Domínguez, G., Cardiel, E., Arias, S. and Rogeli, P. (2013) A Digital Goniometer Based on Encoders for Measuring Knee-Joint Position in an Orthosis. World Congress on Nature and Biologically Inspired Computing, Fargo, ND, 12-14 August 2013, 1-4.
- 25. Kumar, N., Pankaj, D., Mahajan, A., Kumar, A. and Sohi, B.S. (2009) Evaluation of Normal Gait Using Electro-Goniometer. Journal of Scientific & Industrial Research, 68, 696-698.
- 26. Luinge, H.J. and Veltink, P.H. (2005) Measuring Orientation of Human Body Segments Using Miniature Gyroscopes and Accelerometers. Medical & Biological Engineering & Computing, 43, 273-282.
https://doi.org/10.1007/BF02345966 - 27. Kavanagh, J.J. and Menz, H.B. (2008) Accelerometry: A Technique for Quantifying Movement Patterns during Walking. Gait & Posture, 28, 1-15.
https://doi.org/10.1016/j.gaitpost.2007.10.010 - 28. Boutaayamou, M., et al. (2015) Development and Validation of and Accelerometer-Based Method for Quantifying Gait Events. Medical Engineering and Physics, 37, 1-8.
- 29. Tang, K.T. (2007) Fourier Series. In: Tang, K.-T., Mathematical Methods for Engineers and Scientist 3, Heidelberg, Springer-Verlag, Berlin Heidelberg, 3-59.
- 30. Osgood, B. (2011) The Fourier Transform and Its Applications. Electrical Engineering Department, Stanford University, Stanford.
- 31. Grigorescu, L., Oproescu, G., Diaconescu, I. and Simionescu, C. (2011) Fast Fourier Transform and Its Applications. Mathematical Methods in Electrical Engineering and Computer Science, France, University of Galati, Romania.
- 32. Wasylkiwskyj, W. (2013) Fourier Series and Integrals with Applications to Signal Analysis. In: Wasylkiwskyj, W., Signals and Transforms in Linear Systems Analysis, Springer-Verlag, New York, 75-189.
https://doi.org/10.1007/978-1-4614-3287-6_2 - 33. Blickhan, R. (1989) The Spring-Mass Model for Running and Hopping. Journal of Biomechanics, 22, 217-227.
- 34. Hirsch, M.W., Smale, S. and Devaney, R.L. (2005) Differential Equations, Dynamical Systems & an Introduction to Chaos. Elsevier, Berkeley.