Natural Resources
Vol.06 No.03(2015), Article ID:54430,10 pages
10.4236/nr.2015.63013
A Technical Review on Shale Gas Production and Unconventional Reservoirs Modeling
Liang Wang1, Armando Torres1, Li Xiang2, Xu Fei2, Akhona Naido1, Wensi Wu2
1Shale Exploration, Oil and Gas, Western Cape, South Africa
2Resources Oil and Gas Ltd., Western Cape, South Africa
Email: Liang82.wang@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2015; accepted 1 March 2015; published 5 March 2015
ABSTRACT
During the past several years, natural gas production from shale gas is increased and has adsorbed much attention worldwide. The reason behind this is because of advances gained in shale gas recovery techniques from this ultra-low permeability/porosity rock. These techniques are considered the horizontal drilling of the length of 3000 to 5000 ft long and conducting multi-stage hydraulic fracturing along the horizontal portion of the wells. The successful application of above has also driven down the gas prices worldwide and also culminated the security of gas supply for the upcoming decades. This paper is a technical literature review of shale gas production and modeling for future performance evaluation that identifies the current challenges in different stages. Several different and complex physics of gas flow in such a low permeability formation is also explained and the state of the art of the challenges encountered in the modeling process is also explained. As such, gas desorption phenomena, non-Darcy Flow, gas Klinkenberg effect are investigated for different shale formations in the US. This technical review also takes a look over the hydraulic fracturing effects on the economics of shale gas wells due to its straight tie to the production from shale and also the overall recovery from such reservoirs.
Keywords:
Unconventional Shale Gas Reservoirs, Modeling and Simulation, Production Forecast

1. Introduction
Through this century, exponential increase of consumption of oil and gas worldwide is very clear trend. This fact has forced oil and gas industries to look for different and new types of resources underground to meet the growing demand with a similar pace. However, in the past decades, the entire world oil and gas reserves are declining very fast and the reason is the limited availability of new discoveries of new fossil fuels, this also pushes E & P industry toward thinking out of the box. In the recent years, unconventional resources including but not limited tight sands, coalbed methane, gas-hydrates, shale oil, and shale gas, have become very important to provide sufficient hydrocarbon to balance the conventional resources deficit. Considering the natural gas exploration and production, shale gas has attracted many attentions because it presents in huge amounts worldwide and also more identifiable advances gained by industry in this field that resulted in significant enhanced recoveries in shale gas production.
On another point of view, as it is mentioned previously, the amount of fuel reserves worldwide is in a decline trend because of the reduced incidence of significant discoveries of reservoirs worldwide. The generally declining nature of available reservoirs with a substantial number of these in mature life, until techniques to economically recover reserves from unconventional reservoirs were developed. In a simple way, unconventional reservoirs are resources that contain hydrocarbon that are uneconomical to produce at prevailing market rates when conventional recovery and production techniques are implemented. As an outcome of significant breakthroughs in research and technology to boost recovery from low permeability reservoirs, matrix permeability of reservoirs of interest has reduced from milli-Darcies in conventional reservoirs to micro-Darcies in tight gas reservoirs down to nano-Darcies in shale gas reservoirs [1] .
Unconventional resources inherent several specific characteristics, such as very low porosity, permeability, non-Darcy flow, rock surface desorption. All of this affects different aspects of shale from recovery to modeling, simulation and enhancing recovery methods. Most important parameter in shale is considered rock surface desorption that must be well established through experimental data since it makes a big different if it would have been ignored through reserve estimation and future production forecasting [2] [3] . Some studies have suggested that gas desorption from shale rock surface may contribute to extra gas production for EUR from shale gas reservoirs. Cipolla et al. [4] [5] has reported that gas desorption contain up to 22% of the total gas production in 30-year period of production for two major producer in the US, Barnett shale and Marcellus shale. The significant impact of natural gas desorption is primarily seen during the later time of shale horizontal well production that mainly depends on, among other factors, shale reservoir permeability, flowing bottom hole pressure, and hy- draulic fracture spacing. State of the art of literature has shown in average that gas desorption contributes to 20% increase in the EUR during 30-year production performance forecasted for Marcellus shale well that is completed with 12 stages of hydraulic fracturing [6] .
2. Worldwide Shale Gas Assets
Over the recent years, as a result of vast advances in two technologies, multi-stage hydraulic fracturing and long horizontal drilling, many reserves of shale gas around the world that were unknown are now largely exploited with a high pace of recoveries of more shale plays. Figure 1 shows a worldwide distribution of shale gas plays and it is clear the largest reserves are located in the North America/Asian basins considering rough estimates of world shale gas volumes that is to be about 16,000 Tcf [7] [8] . Currently, there is a huge pick in basic investments worldwide by oil and gas companies in shale gas exploration because of the lower geological and commercial development risk and an observed decline rate when compared with conventional plays [9] . The reason behind this is because of the presence of giant shale gas reserves in the subsurface which when discovered makes any project a commercial success at the end.
3. Shale Gas Reservoir Formation
The production of shale gas in the US brought into being a major energy source at the beginning of this century and has increased significantly since. According to the International Energy Agency (IEA), in 2010, shale gas represented more than 20% of the country’s gas production, and it is estimated that by 2035 around 40% of the world’s gas might be unconventional, and shale gas will be the greatest part of it. The US Geological Survey has defined an unconventional reservoir as one with a very large acreage and initially in place hydrocarbon with very low matrix permeability and a low expected final recovery that has no hydrocarbon trap. In shale, the formation serves as both the source rock and the reservoir rock where no migration for the hydrocarbon is occurred and the top of the reservoir is without the presence of a trapping mechanism, i.e. cap rock. In 2010, Aguilera [10] presented his line of thought for different ways that natural gas is stored in shale formations, he suggested (a) natural gas trapped in organic matter; (b) free gas trapped in non-organic matrix porosity, hydraulic and pre-ex-
Figure 1. Map of shale gas resources in the world.
isting natural fracture; (c) free gas also trapped in the micro-fracture porosity.
Unlike conventional gas reservoirs such as sandstone etc., shale formations have very low to ultra-low permeability. Moreover, shale has neighbored the conventional sandstone and carbonate reservoirs that are another reason for considering them as source rock. These shales are considered the source of conventional hydrocarbon accumulations that were migrated upward to accumulate and become trapped in a producible formation below a seal, shale. The organic-matter-rich shales produce uneconomically at usually small amounts of hydrocarbons (gas or oil) through biogenic or thermogenic processes, which is occurred at high pressures through natural fractures and stored in a very low porous reservoir rocks. However, for source shale to offer at commercial value, the quantity of the extracted hydrocarbons was only very low, and a significant amount of hydrocarbon is kept, usually in the form of methane in the matrix pore spaces, pre-existing fractures, and as adsorbed gas onto clay minerals and organic matter, kerogen.
The economic feasibility of all unconventional shale gas resources is attached to creating an effective network of hydraulic fractures, stimulation, in these ultra-low permeability rocks that are on typical values of 0.000001 to 0.00000001 mD [11] . On the other hand, there should be a huge surface area between shale matrix and the created hydraulic fractures in order for shale to be commencing the production, this necessitated the existence of as huge as possible fractures perpendicular to the horizontal wellbore.
4. Complex Physics of Shale Gas Reservoirs
4.1. Gas Desorption
Large portion of shale rock consists of organic matter, kerogenic media. Natural gas methane molecules are adsorbed on the organic rich strata (also they are stored in pore spaces and natural fractures). Thus, significant amounts of natural gas can be produced from the surface of kerogen, which is also known as Total Organic Carbon, TOC [6] . By its very nature, in order to release methane stored within the shale, it is necessary to enhance fluid pathways (create fractures) and deplete the surrounding pressure. As the pressure decreases due to production, more and more adsorbed gas is released from the surface of matrix; this contributes to the total amount of gas produced. Therefore, an adsorption model is required to predict the gas desorbed from shale matrix.
Langmuir adsorption is the most common empirical mathematical model used to quantify the amount of desorbed gas as a function of pore pressure at constant temperature [3] [11] . This analogy comes from the developments made in modeling coal bed methane (pre-shale technology) and it must be noted that sorptive characteristics of shale might not necessarily serve the same way as it does in shale [12] .
Langmuir model simply represents a nonlinear relationship between the potential amount of releasable-gas and the pore pressure given by Equation (1). This equation represents that the potential amount of releasable-gas is just a function of reservoir pressure.
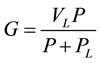 (1)
(1)
where G is the potential releasable-gas content in scf/ton, P is pore pressure (assumed to be the average reservoir pressure) in psi, and VL (Langmuir volume) in scf/ton and PL (Langmuir pressure) in psi are Langmuir constants. Laboratory tests are necessary to determine VL and PL from core samples. Langmuir pressure is defined as the pressure at which 50% of gas is desorbed. By this definition, it is clear that higher the Langmuir pressure reaches, higher the released-gas from the organic shale matter. Langmuir volume is the gas volume at infinite pressure representing the maximum storage capacity of gas, which is a function of TOC of shale sample. Figure 2 shows the experimental values of desorption isotherms for different shales in the US [3] [13] .
4.2. Klinkenberg Effect
Unlike conventional gas reservoirs, shale’s pore size distribution is in the order of micron to nanometer causing seepage of gas molecules to dominate the gas flow. In such a flow condition, formation permeability is not constant anymore and depends on the pressure. The gas slippage known as Klinkenberg effect is very significant and might not be ignored while modeling shale gas flow. Klinkenberg effect, [14] , presents a nonlinear relationship between absolute permeability and pore pressure given in Equation (2).
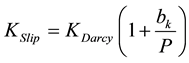 (2)
(2)
where 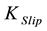 is modified permeability for slippage,
is modified permeability for slippage,  is shale rock permeability,
is shale rock permeability, 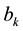 in psi is Klinkenberg slippage factor and P is reservoir pressure.
in psi is Klinkenberg slippage factor and P is reservoir pressure.
Many authors studied the Klinkenberg slippage factor, 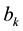 , to correlate it to effective permeability. Jones and Owens [15] conducted experiments on 100 samples of tight gas plays in the US and proposed an empirical formula, Equation (3).
, to correlate it to effective permeability. Jones and Owens [15] conducted experiments on 100 samples of tight gas plays in the US and proposed an empirical formula, Equation (3).
 (3)
(3)
Several empirical and semi-empirical correlations have been developed to modify Klinkenberg effect for shale reservoirs. Among them, Fathi [16] introduced Equation 4 for double-slip Klinkenberg equation (quadratic
Figure 2. Adsorption isotherms for different shale formations in the US.
expression) for gas flow in nano-pores that is shown to be applicable for many industrial and technological applications using lactic Boltzmann simulation.
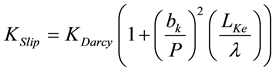 (4)
(4)
where λ is the mean free path of the gas molecules and 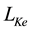 accounts for kinetic energy of molecules bouncing back.
accounts for kinetic energy of molecules bouncing back.
4.3. Non-Darcy Flow
The relationship between the pressure drop and the flow rate during fluid flow through porous media is known to be affected by the oscillation in the flow rate [17] . At low flow rates, the pressure drop are linearly proportional to flow rate (Darcy flow is followed); at higher flow rates, the pressure drop exceeds the predictions by Darcy flow. This phenomenon is known as non-Darcy flow behavior. In shale formations, gas velocity in fractures is very high; the flow pattern deviates from Darcy flow; it is necessary to consider a second degree polynomial, Equation (5), of Forchheimer to account for non-Darcy flow into gas flow modeling.
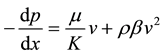 (5)
(5)
where dp/dx is pressure gradient, v is gas velocity, μ is fluid viscosity, K is effective permeability of rock, ρ is fluid density and β is the non-Darcy coefficient in 1/ft.
In order to predict the β factor, there are several equations connecting β to porosity, permeability and tortuosity. In this paper, we focused on the equations that assumed β factor as a function of medium permeability given by Equation 6. The general form of this equation is expressed below.
 (6)
(6)
where a and b are constants determined with laboratory experiments. An estimate for the acceptable ranges of a and b for different rocks are provided below. This range differs from unconventional formations on the lower bound to a conventional rock on the upper bound.
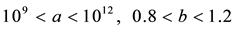
It is assumed that a is equal to 109 and b equal to 1 [18] [19] .
5. Reservoir Simulation and Modeling of Shale
Due to the complex nature of hydraulic fractures and its network with pre-existing natural fractures and also very low permeability of shale reservoirs that is combined with horizontal completion, as always, reservoirs simulation is the cheapest and commonly preferred approach to evaluate and predict the performance of such complicated reservoirs. Numerical simulation techniques are widely accepted and sued in the oil and gas industry; however, some semi-analytical tools are also developed and is available in the literature [20] [21] , the specific characteristics of such tools are considered being simple and fast which is valuable and helpful in the decision making processes although ignore most physics of shale compared to conventional wells. The most important problem when using analytical or semi-analytical models are that they lack to capture the linear transient behavior of production in shale. This kind of behavior is due to the very low permeability of shale rock matrix. One way to improve these methods accuracy is combing them by the numerical simulations to capture the entire window of production. In simulation of shale formation compared to simulating conventional assets, the computational cost and run time of simulation of discretized grids of entire reservoir including network of hydraulic and natural fractures, and unstimulated area is extremely high that requires some techniques implemented such as predictive modeling.
On another note, more specifically, it should be noted that Darcy flow and capillary equilibrium state already implemented in commercial simulators for conventional reservoirs are inaccurate for reliable simulation and production evaluation from shale gas reservoirs [22] [23] . As of today, many developed capabilities of commercial reservoir simulators are not accurately implemented as they are not directly affecting any portion of production behavior of shale reservoirs and this put a big black dot in the result and how they are representing the actual trends observed in the real fields [24] . Andrade [23] recognized the branches where commercial simulators reaches unrealistic estimates unacceptable for shale gas reservoirs, these are outlined as (a) the assumption of instantaneous capillary equilibrium; (b) that Darcy flow gives a complete description of the flow regime; (c) that relative permeability is not rate dependent.
6. Governing Equations of Two-Phase Flow in Shale
Generally, two-phase fluid flow of water and gas in a model is considered in constructing the geologic model of shale gas reservoirs. For instance, the dual-permeability model considers the intercommunication between the inter-granular void spaces in contrast to the dual-porosity model. Also, this model considers flow in two domains including the matrix and fractures. This model also allows the transfer of both gas and water between the matrix and fracture domains gas velocity in the matrix and fracture domain is calculated with Equations (7) and (8):
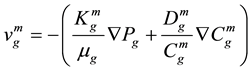 (7)
(7)
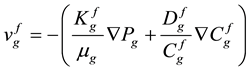 (8)
(8)
where 







where, vw is water velocity, Kw is water permeability, Pw is water pressure, and μw is water viscosity.
6.1. Flow in Matrix
The equations of gas transport thus are simplified for matrix domain as shown in Equation (11):

where Z is the gas compressibility factor, R is the gas constant, T is Temperature, M is gas molecular weight, and 

where 


6.2. Flow in Fracture
After some manipulation and simplifications, the gas flow governing equation in fracture becomes as the following, Equation (13):

For the water phase, Equation (14) represents the related formula.

Equations (15) to (18) represent the auxiliary relations used in the solution method.




7. Factors Affecting Production from Shale
There are many factors that affect gas production from shale; in this section the most significant parameter has been described. These factors are divided into three sections, geological, economic issues and technological aspects. The geology of shale gas formation and the productivity of the well drilled as well as availability of water are considered very important and apart from economic issues such as additional cost of horizontal drilling, completions and fracturing parameters and also more importantly fluctuating gas prices, cost of leasing the land and etc. are key elements in the profitability of a project. Some of the most influencing parameters are as below:
1) Matrix porosity;
2) Thickness of shale zone;
3) Inside distance that is horizontal well placement in a pad-drilled situation;
4) Injected proppant volume.
The potential of hydrocarbon available in an economical level is determined by other parameters such as Total Organic Carbon (TOC), kerogen type, thermal maturity and gas content of specific shale formations that varies widely from place to place. Above also affect the quality of the gas produced that ultimately affects the eco- nomic viability of the project. From a petro-physical point of view, it is very important to notice that two parameters, porosity and permeability, of the formation should be accurately measured as it directly affect the original gas in place calculation along with the desorption characteristics of the shale rock.
8. Shale Unique Petro-Physical Property, Permeability
In 2009, Freeman noticed that based on the acceptance of continuum flow, the Darcy law is applicable is shale but however, Javadpour [25] has suggested the continuum law is not appropriate and fails when applied to shale formations as it is in nano-scale and mean free path of the gas molecules are very small. A very accurate determination of permeability is a key in reservoir characterization of shale resources. Especially in shale, using traditional methods applied to conventional will not produce an accurate result for shale due to its very complex nature, therefore, the process f measuring shale permeability is very challenging. Moreover, permeability measurements of shale rock in different laboratories with entirely different methods have given different according to [26] . As a result, some advances in technologies for reliable measurements of shale formation permeability are developed such as pulse decay method and some even with steady state methods.
In 2010, Aguilera suggested that flow in shale occurs through mega-pores, macro pores, meso-pores and micro pores. On another note, diffusion flow in shale nano pores are deviating from Darcy law as a consequence of Klinkenberg slippage effect and inertial flow [27] . It is concluded that by ignoring the non-Darcy flow, results obtained from laboratory measurements will lead to significant errors when determining permeability. There are also some advances in steady state methods that have minimized these effects but again they are not completely eliminative.
9. Hydraulic Fracturing of Shale Reservoirs
As it is mentioned previously, to achieve an economic viable natural gas production form shale formations, hydraulic fracturing is become a standard practice. A complete and accurate hydraulic fracturing is achieved by pumping slick water, proppant that is injecting very high pressurized flow into the shale formation to create network of fractures. Due to higher pressure exerted on the formation, a fracture is created that in most simulations studies are considered perpendicular to the horizontal wells. Also, the length of the fractures are assumed equal in both sides of the horizontal wells that should be carefully used in each formation due to different issues such as rock compaction around wellbore. The length of the fracture on one side of the wellbore is referred to as the fracture half-length, Figure 3 depicts schematic of a hydraulic fracture.
On a different note, due to brittleness of shale formations, a very huge fluid pressure is required for creating a very efficient hydraulic fracturing network as it is considered the heart of production form shale. The brittleness and ductileness of shale formation depends on the ratio of quartz/clay minerals. This ratio is an indicator of these parameters that govern the propagation of hydraulic fractures [28] [29] . At the end, successful application of hydraulic fracturing is proven to be valid method to unlock production from these previously known un-pro- ducible formations due to their nano-Darcy permeability.
The more proppant is injected the larger hydraulic fractures is achieved. However, it should be noted that an optimized injection rate is necessary since a very large hydraulic fracture may breaks into the water zone and causes further problems such as two phase flow and relative permeability issues for gas flow. This fact will be detrimental to the production from shale and must be given a careful attention. This fact aside other factors, a large number of well-sized hydraulic fractures are very desirable compared to very large hydraulic fractures but in less density.
The last but not least unique characteristics of shale reservoirs are encountering a very high capillary pressure that causes fluid imbibition that retains fracturing fluid. Water blockage is directly depends on the previous phenomena that is the existence of a region with very high water saturation that reduces the mobility of natural gas in the rock and prevents its movements [30] [31] . Fast cleanup of the horizontal wellbore and shale formation is very critical in order to improve the natural gas production [32] [33] .
10. Production Forecasting in Shale Reservoirs
The sensitivity of production from shale wells to the size and the conductivity assigned to the Stimulated Reservoir Volume explains the uncertainties associated with the forecasts that are made using this technique. Furthermore, SRV techniques are incapable of making serious contribution to designing an optimum frac-job specific to a given well. According to the available production data form unconventional shale reservoirs, a well by well basis use of decline curve analysis is very common where in conventional assets it is possible to use on both well scale and field scale sizes [34] .
Production from unconventional gas reservoirs are shown in Figure 4, Three dominant flow regimes are defined for the flow of natural gas from the shale matrix and through the hydraulic fractures toward the horizontal wells and ultimately to the well production.
(1) Very early time flow period where the flow is from the hydraulic fractures;
(2) The intermediate time period when the flow is from the matrix and the fractures;
(3) The late time period when the flow is predominantly from the matrix.
One of the major problems of Decline Curve Analysis (DCA) is its lack of sensitivity to major physical phenomena in shale wells that is related to the fluid flow, the hydraulic fracture, and its unique reservoir characteristics. In cases like newly found resources, where short periods of production data are available, the use of decline curve analysis results in very wrong estimations. There is always an over-estimation of reserves by a fac-
Figure 3. Hydraulic fractures perpendicular to the horizontal well.
Figure 4. Flow regimes in shale wells.
tor or 2 to 5 if Arps is used for unconventional gas reservoirs which are because of higher b factor greater than 1 as opposed to a hyperbolic exponent of between 0.0 and 1.0 for boundary dominated flow [34] - [36] . Moreover, power law or stretched exponential methods are also developed after decline curve analysis that works accurately for forecast purposes. Last but not least, the use and implementation of this method is required to be deployed in commercial softwares [37] [38] .
11. Conclusions
By drilling more and more wells in Shale formations, reservoir engineering and modeling are gaining their right places in the asset management of these important energy resources. The presence of highly complex multi- cluster, multi-stage hydraulic fractures has significantly complicated the simulation and modeling of production from shale. As stated by the results of the literature demonstrate that minimum ingredients required to model shale gas reservoirs are: (1) Considering desorption phenomena; and (2) Considering pressure-dependent permeability for hydraulic and induced-fractures into the flow governing equations. Consequently, it is unnecessary to add more mechanisms and nonlinearity into the model.
The limitations of our understanding of this complex phenomenon have resulted in limitations in our ability to perform accurate modeling of the production from shale formations which consequently have resulted in making significant assumptions to make our models work. Use of predictive models such as CRM, newly developed Arps equation, AI & DM, Data-driven modeling will help validate the results of numerical simulation for evaluating shale gas reservoir performance and forecasting production. However, a careful attention should be given while using these methods.
References
- Kundert, D. and Mullen, M. (2009) Proper Evaluation of Shale Gas Reserves Leads to a More Effective Hydraulic Fracture Stimulation. SPE Paper No. 123586. Presented at the SPE Rocky Mountain Petroleum Technology Conference, Dever, 14-16 April 2009, 11 p. http://dx.doi.org/10.2118/123586-MS
- Eshkalak, M.O., Mohaghegh, S.D. and Esmaili, S. (2013) Synthetic, Geomechanical Logs for Marcellus Shale. Paper SPE 163690 Presented at Digital Energy Conference and Exhibition, The Woodlands, 5-7 March 2013.
- Eshkalak, M.O., Aybar, U. and Sepehrnoori, K. (2014) An Integrated Reservoir Model for Unconventional Resources, Coupling Pressure Dependent Phenomena. Paper SPE 171008 Presented at Eastern Regional Meeting, Charleston, 21-23 October 2014.
- Cipolla, C.L. and Lolon, E.P. (2010) Reservoir Modelling in Shale Gas Reservoirs. SPE Paper No. 125530 Presented at the SPE Eastern Regional Meeting, Charleston, 23-25 September 2009.
- Cipolla, C., Mack, C. and Maxwell, S. (2010) Reducing Exploration and Appraisal Risk in Low-Permeability Reservoirs Using Microseismic Fracture Mapping. SPE Paper No. 137437 Presented at the Canadian Unconventional Resources & International Petroleum Conference, Calgary, 19-21 October 2010.
- Mengal, S.A. and Wattenbarger, R.A. (2011) Accounting for Adsorbed Gas in Shale Gas Reservoirs. Paper SPE 141085 Presented at the SPE Middle East Oil and Gas Show and Conference, Manama, 25-28 September 2011, 15 p. http://dx.doi.org/10.2118/141085-MS
- Fazelipour, W. (2010) Innovative Simulation Techniques to History Match Horizontal Wells in Shale Gas Reservoirs. SPE Paper No. 139114 Presented at the SPE Eastern Regional Conference, Morgantown, 12-14 October 2010.
- Aybar, U. (2014) Investigation of Analytical Models Incorporating Geomechanical Effects on Production Performance of Hydraulically and Naturally Fractured Unconventional Reservoirs. M.Sc. Thesis. The University of Texas at Austin, Austin.
- Fazelipour, W. (2011) Innovative Reservoir Modelling and Simulation of Unconventional Shale Gas Reservoirs Powered by Microseismic Data. SPE Paper No. 141877 Presented at the SPE Middle East Unconventional Gas Conference and Exhibition, Muscat, 31 January-2 February 2011, 14 p. http://dx.doi.org/10.2118/141877-MS
- Aguilera, R. (2010) Flow Units: From Conventional to Tight Gas to Shale Gas Reservoirs. SPE Paper No. 132845 Pres- ented at the Trinidad and Tobago Energy Resources Conference, Trinidad, 27-30 June 2010, 16 p. http://dx.doi.org/10.2118/132845-MS
- Eshkalak, M.O., Aybar, U. and Sepehrnoori, K. (2014) An Economic Evaluation on the Re-Fracturing Treatment of the US Shale Gas Resources. SPE Eastern Regional Meeting, Charleston, 21-23 October 2014, SPE-171009-MS.
- Leahy-Dios, A., Das, M., Agarwal, A. and Kaminsky, R.D. (2011) Modeling of Transport Phenomena and Multicomponent Sorption for Shale Gas and Coalbed Methane in an Unstructured Grid Simulator. SPE Annual Technical Conference and Exhibition, Denver, 30 October-2 November 2011, SPE-147352-MS.
- Aybar, U., et al. (2014) The Effect of Natural Fracture’s Closure on Long-Term Gas Production from Unconventional Resources. Journal of Natural Gas Science and Engineering, 21, 1205-1213. http://dx.doi.org/10.1016/j.jngse.2014.09.030
- Klinkenberg, L.J. (1941) The Permeability of Porous Media To Liquids and Gases. Drilling and Production Practice, New York, 1 January 1941, API-41-200.
- Jones, F.O. and Owens, W.W. (1980) A Laboratory Study o Low Permeability as Sands. Journal of Petroleum Technology, 32, 1631-1640. http://dx.doi.org/10.2118/7551-PA
- Fathi, E., Tinni, A. and Akkutlu, I.Y. (2012) Correction to Klinkenberg Slip Theory for Gas Flow in Nano-Capialries. International Journal of Coal Geology, 103, 51-59. http://dx.doi.org/10.1016/j.coal.2012.06.008
- Forchheimer, P.H. (1901) Wasserbewegung durch Boden [Movement of Water through Soil]. Zeitschrift fur Acker und Pflanzenbau, 49, 1736-1749.
- Abiodun M.A. (2007) Mathematical Model for Darcy Forchheimer Flow with Applications to Well Performance Analysis. MS Thesis, Texas Tech University, Lubbock.
- Aybar, U., Eshkalak, M.O., Sepehrnoori, K. and Patzek, T.W. (2014) Long Term Effect of Natural Fractures Closure on Gas Production from Unconventional Reservoirs. SPE Eastern Regional Meeting, Charleston, 21-23 October 2014, SPE-171010-MS.
- Medeiros, F., et al. (2007) Productivity and Drainage Area of Fracture Horizontal Wells in Tight Gas Reservoirs. Rocky Mountain Oil & Gas Technology Symposium, Denver, 16-18 April 2007, SPE-108110-MS.
- Kazemi, H. (1969) Pressure Transient Analysis of Naturally Fractured Reservoir with Uniform Fracture Dimensions. Society of Petroleum Engineers Journal, 9, 451-462.
- Quin, B. (2007) Numerical Study of Recovery Mechanisms in Tight Gas Recovery. MS Thesis, The University of Oklahoma, Norman.
- Andrade, J., Civan, F., Devegowda, D. and Sigal, R. (2010) Accurate Simulation of Shale Gas Reservoirs. SPE Annual Technical Conference and Exhibition, Florence, 19-22 September, SPE-135564-MS. http://dx.doi.org/10.2118/135564-MS
- Eshkalak, M.O., et al. (2014) Simulation Study on the CO2-Driven Enhanced Gas Recovery with Sequestration versus the Re-Fracturing Treatment of Horizontal Wells in the US Unconventional Shale Reservoirs. Journal of Natural Gas Science and Engineering, 21, 1015-1024. http://dx.doi.org/10.1016/j.jngse.2014.10.013
- Javadpour, F., Fisher, D. and Unsworth, M. (2007) Nanoscale Gas Flow in Shale Gas Sediments. Journal of Canadian Petroleum Technology, 46.
- Freeman, C.M. (2010) A Numerical Study of Microscale Flow Behavior in Tight Gas and Shale Gas Reservoir Systems. SPE Annual Technical Conference and Exhibition, Florence, 19-22 September 2010, SPE-141125-STU.
- Rahmanian, M., Solano, N. and Aguilera, R. (2010) Storage and Output Flow From Shale and Tight Gas Reservoirs. SPE Western Regional Meeting, Anaheim, 7-29 May 2010, SPE-133611-MS. http://dx.doi.org/10.2118/133611-MS
- Norton, M., Hovdebo, W., Cho, D. and Maxwell, S. (2010) Surface Seismic to Microseismic: An Integrated Case Study from Exploration to Completion in the Montney Shale of NE British Columbia, Canada. 2010 SEG Annual Meeting, Denver, 17-22 October, SEG-2010-2095.
- Miller, C., Lewis, R. and Bartenhagen, K. (2007) Design and Execution of Horizontal Wells in Gas Shales Using Borehole Images and Geochemical Data. SEG Denver 2010 Annual Meeting, AAPG SW Section Convention.
- Gupta, D.V.S. (2009) Unconventional Fracturing Fluids for Tight Gas Reservoirs. Presented at the 2009 SPE Hydraulic Fracturing Technology Conference, The Woodlands, 19-21 January 2009.
- Mazzer, R.L. (1997) Liquid CO2 Improves Fracturing, Hart’s Oil and Gas World. Hart’s Oil and Gas World, 22.
- Slatter, T.D., Rucker, J.R. and Crisp, E.L. (1986) Natural Gas Stimulation in Tight, Clay-Bearing Sandstone Using Foamed CO2 as Hydraulic Fracturing Media. Presented at the Unconventional Gas Technology Symposium of the Society of Petroleum Engineers, Louisville, 18-21 May 1986.
- Eshkalak, M.O., Mohaghegh, S.D. and Esmaili, S. (2014) Geomechanical Properties of Unconventional Shale Reservoirs. Journal of Petroleum Engineering, 2014, Article ID: 961641. http://dx.doi.org/10.1155/2014/961641
- Strickland, R., Purvis, D. and Blasingame, T. (2011) Practical Aspects of Reserve Determinations for Shale Gas. SPE North American Unconventional Gas Conference and Exhibition, The Woodlands, 12-16 June 2011, SPE-144357-MS. http://dx.doi.org/10.2118/144357-MS
- Arps, J.J. (1945) Analysis of Decline Curves. Transactions of the AIME, 160, 228-247. http://dx.doi.org/10.2118/945228-G
- Eshkalak, M.O., Al-Shalabi, E.W., Aybar, U. and Sepehrnoori, K. (2014) Enhanced Gas Recovery by CO2 Sequestration versus Re-fracturing Treatment in Unconventional Shale Gas Reservoirs. Abu Dhabi International Petroleum and Exhibition and Conference, Abu Dhabi, 10-13 November 2014, SPE-172083-MS.
- Cipolla, C., Mack, M. and Maxwell, S. (2010) Reducing Exploration and Appraisal Risk in Low-Permeability Reservoirs Using Microseismic Fracture Mapping-Part 2. SPE Latin American & Caribbean Petroleum Engineering Conference, Lima, 1-3 December 2010, SPE-138103-MS.
- Omidvar Eshkalak, M. (2013) Synthetic Geomechanical Logs and Distributions for Marcellus Shale. MSc Thesis, West Virginia University, Morgantown.
Nomenclature
Symbols
B Formation volume factor
c Compressibility
C Concentration, constant related to the heat of adsorption
D Diffusivity
G Gas content
K Permeability
Mg Gas molecular weight
P Pressure
PL Langmuir pressure
Po Saturation pressure of the gas
qg Gas mass flow rate
R Universal gas constant
s Saturation
T Temperature
v Velocity
VL Langmuir volume
Vm Maximum adsorption gas volume
V(p) Gas volume of adsorption
Z Gas compressibility factor
ϕ Porosity
µ Viscosity





