Natural Resources
Vol.4 No.5(2013), Article ID:36541,9 pages DOI:10.4236/nr.2013.45045
Small-Scale Spatial Patterns of Copernicia alba Morong near Bahia Negra, Paraguay
![]()
School of Forest Resources and Environmental Science, Michigan Technological University, Houghton, USA.
Email: *bdorr@mtu.edu
Copyright © 2013 Michelle E. Cisz et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 23rd, 2013; revised July 20th, 2013; accepted July 31st, 2013
Keywords: Ripley’s K-Function; First Order Analysis; Floodplain; Fire; Chaco; Monotypic Stands; Disturbance Ecology; Population Dynamics
ABSTRACT
We assessed the spatial distribution of Copernicia alba Morong. In the study area, a lowland palm savanna floodplain, C. alba is the only overstory species. We hypothesized C. alba would be randomly distributed within natural stands. Palms were tallied in six randomly located 0.25 ha plots and analyzed using a first-order, Ripley’s K function to assess the distribution of juvenile, adult, and total palm populations. While the total population had either aggregated or random distributions, when analyzing juvenile and adult population separately, we found juveniles were consistently more aggregated than the adults.
1. Introduction
The spatial distribution of plant species is considered an important ecological subject as distribution results from and mediates complex ecological processes [1]. Studies of the spatial distribution of palms and trees may be purely descriptive, (this was especially true for the early theoretical development of spatial distribution models) [2,3]; they are designed to elicit the underlying ecological mechanisms for the patterns [4,5], or observe or infer changes in and the dynamics of spatial distribution over time [1,4,6]. Frequently studies contain elements from all three purposes; for example, it is the underlying ecological processes that may drive temporal changes in species distribution [1,7,8].
Ecologists have hypothesized that plant distribution may be based on seed dispersal patterns [4,9], underlying heterogeneity of local environment [1,10], competition or facilitation between plants—both within and between species [5-7,11], climate [12], and relative abundance of a species within the plant community [13]. Ecological factors influencing plant distributions may include moisture availability [14], soil heterogeneity [1,15], topography [16,17], inter-specific competition [18-22], and seed dispersal [11,23-25]. The plant’s role in temporal succession, intraspecific competition, along with forest structure have also been explored as variables [22,26,27] specific to the plant rather than its environment and can be scale dependent [11].
Physical patterns within the landscape such as soil, moisture or topography may generate patterns that are dissimilar from the pattern that would develop in a more uniform landscape [28]. For example, seedlings and juveniles of Borassus aethiopum, an African savanna palm, are more aggregated than adults and the aggregated clusters tend to occur on sites with better nutrient status [1]. In general, spatial heterogeneity of resources [29,30] and species diversity [31] may increase aggregation. A single plant species may aggregate when growing in heterogenous landscapes and in dense enough stands to generate competition between plants even when the pattern for all species combined is not aggregated [32].
Populations may have different distributions at different scales [2,5,11,13]. Plants may be aggregated at larger scales but plant competition generates a more regular pattern at smaller scales [3]. In the early stages of plant establishment species may benefit from the protection or the amelioration of soil properties provided by a more mature plant, fostering aggregation of plants. This is especially true in arid and semi-arid environments [6].
Skellam’s [3] paper on theoretical random distributions of plants assumed an open environment, one recently disturbed so that initially there is no inter-specific competition and one where the plants’ environment is uniform. Most studies of spatial distribution include more than one species and some form of spatial heterogeneity. For example, in a study of different tropical forests almost all species were aggregated and none were dispersed; however, the number of species in the forest ranged from 70 to over 800 [33]. Pillay and Ward’s study [34] of the small woody tree Acacia karroo is an exception; all trees in their study plots were Acacia karroo. The purpose of our study was to examine the spatial distribution of Copernicia alba (Arecaceae) without the confounding influences of inter-specific overstory competition or a heterogenous environment. Our study location contained only one overstory species, Copernicia alba, and the study plots were located on uniform flat section of the Chaco of Paraguay near Bahía Negra, but distant from the Rio Paraguay. We used Ripley’s K function as it allows for independent testing for random, aggregated or dispersed distribution at different scales. Our null hypothesis was that species would be randomly distributed at all measured scales.
2. Methods
2.1. The Gran Chaco Basin
The Chaco is part of a Pleistocene Epoch lake that deposited a thick layer of fine-grained sediment and poorly drained soils along the Chaco’s northeastern edge [35,36]. Fire is a historically common disturbance agent in the dry and humid Chaco and throughout the neighboring Pantanal wetland [37,38]. The Paraguay River system supports a landscape of monotypic stands of naturally regenerated palm forest intermixed with riparian edges rich in species characteristic of the Brazilian Amazon, Cerrado, and Humid Chaco [35,39-43].
2.2. The Study Area
The study area is located between the Pantanal wetlands and the Humid Chaco forest, approximately 13 km west of the Paraguay River, W20˚04'5", S58˚17'16", with elevations of 82 - 85 m. Temperature ranges from 12˚C - 40˚C with an average rainfall of 995 mm/year [44,45]. The rainy season is from September to April, with December and January having the greatest rainfall [45,46]. The dry season is from August to October when hot northerly winds and wild fires are more common [47]. The region has a return fire interval of one to five years. Key informants described the study area as being grazed in the 1970s by approximately 3000 cattle and palms were harvested until a major flood had forced owners to move to higher lands. The land is currently operated as a biological reserve maintained by Guyra Paraguay, a nonprofit organization.
Plot locations were chosen randomly within the study area and were located within 0.5 km of two focal points. Each plot was a 50 × 50 m quadrat. The plots are not replicates and statistical analysis was performed on each plot separately.
C. alba dominates both the overstory and the midstory throughout the study area. The understory is codominated by members of Poaceae and Fabaceae family (Acacia and Albizia genera). Members of the Verbenaceae, Asteraceae, and Apocynaceae families can also be found in the understory.
2.3. Copernicia alba
C. alba is 10 to 13 meters tall, with a maximum height of 25 m [48-51]. It is monoecious and generally does not produce flowers or seeds until it reaches at least 3 m in height [52,53]. C. alba blooms between the months of August to October [46,53,54]. Fruits are 1.0 to 1.5 cm in diameter [50,55]. The rachises that carry seeds grow from the center of the crown and can range from 0.5 m to 2 m in length. Fruit are produced irregularly throughout the seasons and the majority of individuals drops their seed fruits in the late dry season (winter) with the onset of sporadic rainfalls, strong northern winds, and fire season [46,54]. In the open canopied savanna C. alba is exposed to strong winds that could aid in dislodging the light fruits [56]. C. alba’s role with many of the endangered fauna and migratory birds has received limited study. Birds, small rodents, and native herbivores such as the greater rhea (Rhea Americana) and white-lipped peccary (Tayassu pecari) could play a role in dispersing seed [4,53,56,57]. Other studies have shown that herbivory may increase aggregation [4] or lead to a more regular dispersion, especially in more diverse plant communities [58]. The corky vascular meristems of palms make them resistant to most savanna fires while seconddary adventitious roots sustain the palm in times of flooding [11].
Copernicia alba Morong has been documented from latitudes 14˚S to 27˚S and longitudes 56˚03'W to 66˚00'W, along the Pilcomayo and Paraguay Rivers. Mature palms occupy the overstory in both forest and grassland habitats. Within forests, C. alba can codominate the overstory and midstories. Throughout the Chaco C. alba is associated with planar alluvial flood zones that cycle between floods and long periods of drought [46, 53,59-61].
2.4. Study Design
A preliminary trip to the savanna was made in April of 2010 and the first dataset was collected from Plots 1 - 3 during the middle of the dry season (winter) 2010. Field measurements for Plots 4 - 6 were taken during the end of a light drought in November, 2010.
Within each plot all palms with a stem height of at least 1 m were located using a handheld global positioning system (GPS) (Garmin Etrex, Garmin Ltd., Kansas, USA). Several sets of ground-truthed points showed that the measurements were accurate within 1 to 2 m. Diameter at breast height (DBH) was recorded only for palms of at least 1.5 m in height and lacking thick petiole sheaths which would bias diameter measurements. Any palms completely defoliated or showing signs of stem damage were included in the data set, however dead palms were excluded. We define juveniles in this study as having established stem heights greater than or equal to 1.0 m and less than 3.5 m. Adults have stem heights greater than or equal to 3.5 m. Heights do not include crowns, but were measured to the stem apex. The hypsometer technique was used to measure the heights of palms greater than or equal to 5 m while the height of shorter palms were measured directly using a flagged pole that was 3 m in height. Herbarium samples were submitted to Universidad Nacional de Asunción to assist in identification.
2.5. Data Analysis
The transformed Ripley’s K function, L(r), tests for complete spatial randomness in the distribution of palms (i.e., to test if the observed palm locations are distributed via a homogenous Poisson process [62]) by determining the expected and observed number of palms within the radius, r, of each palm within the sample plots. The transformed Ripley’s K function, which was calculated using the Spatstat package [63] in the R statistical software package [64], was used to determine the spatial distribution of the total palms population with stems greater than or equal to 1 m in height [63]. After analyzing the total palm population with the transformed Ripley’s K function, the palms were separated into adult (stem height greater than 3.5 m) and juvenile classes (stem height less than 3.5 m) [52,53]. The juvenile and adult populations were then analyzed using the Ripley’s K function.
The three palm populations (total, juvenile, and adult), were analyzed in each of the six plots, yielding 18 different graphs of the transformed Ripley’s K function. The null hypothesis for all 18 calculation sets was that the spatial distribution of the given population followed complete spatial randomness (i.e., it follows a homogenous Poisson process). The alternative hypothesis was that patterns were either aggregated or dispersed (dispersed is sometimes described as uniform, regular or repulsed).
3. Results
A total of 363 palms were sampled in the six plots. The palms/ha, basal area, stand structure (juvenile: adult ratio), and the mean height varied considerably from plot to plot (Table 1) [65]. Plot 1 had the largest number of juveniles (43), and Plot 2 has the smallest with 14 individuals. Plot 4 had the largest number of adults (51). Plots 3 and 6 had approximately 1:1 ratios of adults to juveniles (Table 1). Basal area and palm densities varied among the six plots (Table 1). Plot 4 has the highest basal area and palm densities, with 63% of the population represented by adult palms.
3.1. Total Palms Population
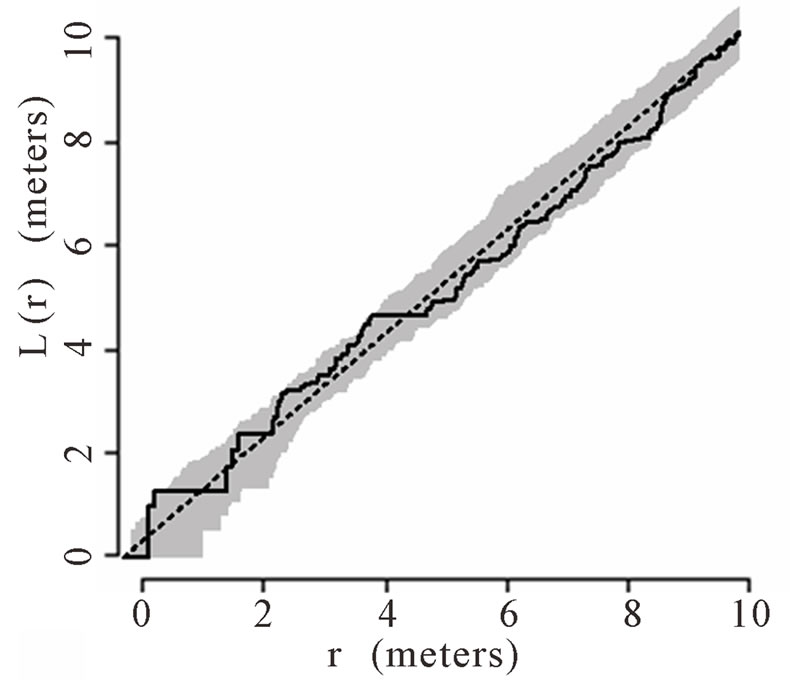
The theoretical (under the hypothesis of complete spatial randomness) and observed distribution of palms were generated using the transformed Ripley’s K function and plotted for all palms. The transformed Ripley’s K function, L(r), was calculated for each radius, r, based on the observed data in each of the six plots. The transformed Ripley’s K function allows assessment of patterns at different radii or local scales, ranging from 0 to 12 m within the 50 m × 50 m plots. The calculation of L(r) generates values of L(r) for each radial distance, r, that are independent of one another and independent of palm density. Each graph shows a straight line passing through the origin that represents theoretical L(r) if the distribution of palms was generated via a homogenous Poisson process (i.e., they follow a complete spatial random pattern). Thirty-nine Monte Carlo simulations were calculated to generate confidence envelopes (shown in gray in the figures) with a significance level of alpha = 0.05 [64,66]. When the observed L(r) value is greater than the theoretical L(r) and lies above of the gray 95% confidence envelope, the null hypothesis of complete spatial randomness is rejected, and the pattern is considered aggregated. When the observed L(r) is less than the theoretical L(r) and below the 95% confidence envelope, the null hypothesis of complete spatial randomness is again rejected, and the pattern is considered dispersed.
When Ripley’s K function was calculated for palms with a stem height greater than 1 m, aggregation and spatial randomness were not consistent across all six plots. Both aggregated and spatially random distributions were found at various scales (i.e., r values) in Plots 1, 2, 5, and
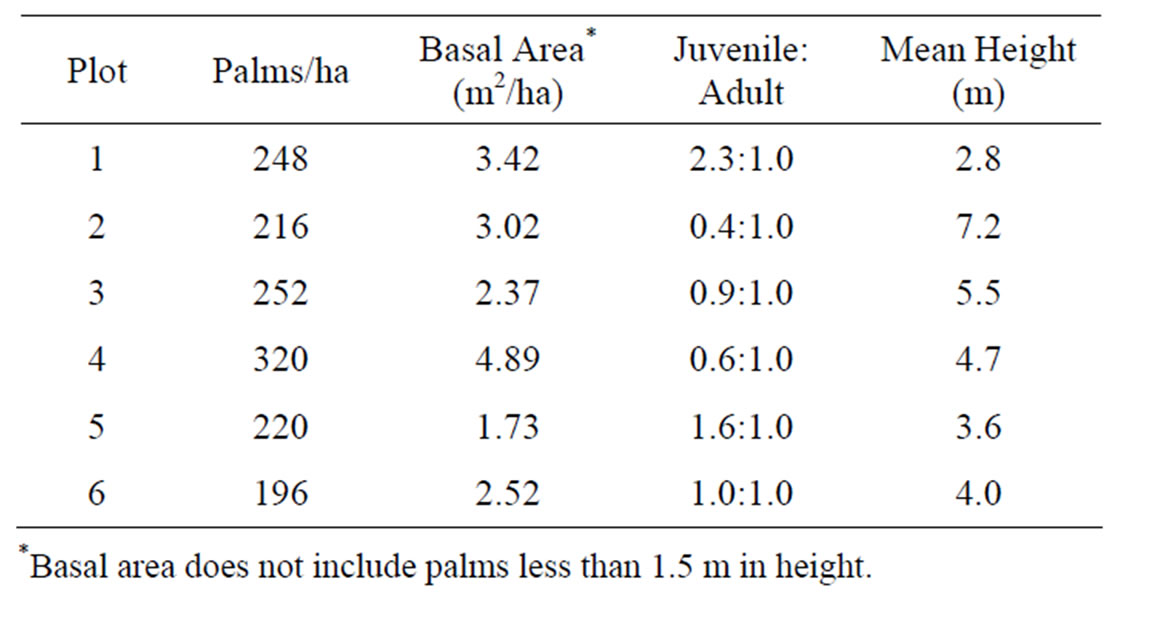
Table 1. Univariate statistics for palm populations on each plot.
6 (Figures 1(a), (b), (e), and (f) respectively). Plots 3 and 4 had spatially random distributions at all scales (Figures 1(c), (d)). Plot 3 patterns fluctuated above and below the theoretical line for a spatially random distribution while Plot 4 exhibited random patterns with patterns of aggregation at all scales.
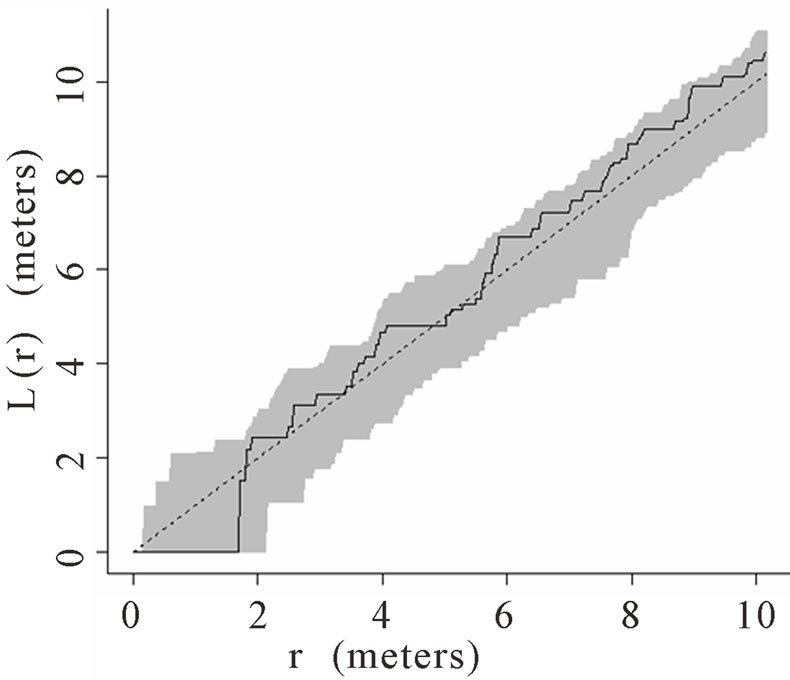
3.2. Juveniles and Adults
When the data set was separated by developmental classes, juveniles tended to aggregate while adults were more randomly distributed. This occurred in Plots 1 (Figures 2(a), 3(a)), 4 (Figures 2(d), 3(d)), and 5 (Figures 2(e), 3(e)). For Plots 3 (Figures 2(c), 3(c)) and 6 (Figures 2(f), 3(f)) both juveniles and adults were randomly distributed; however, the adults had lower L(r) values than the juvenile populations for most scales. Plot 2 (Figures 2(b), 3(b)) was the exception with aggregated adult palms from 6 to 12 meters radius and aggregated juvenile palms when the radius was less than 9 meters; otherwise palms were randomly distributed. The juveniles of Plot 2 (Figure 3(b)) have higher L(r) values than the adults from 2 to 12 m. Most adult aggregation in this plot was caused by two linear groups of palms.
In Plot 1 (Figure 3(a)) aggregation was observed among juveniles at distances from 2 m to 12 m and adults were randomly distributed at distances 0 to 12 m. This plot had the greatest number of juveniles and the lowest number of adults of all six plots (Table 1).
The same basic pattern, where juveniles were aggregated while adults were randomly distributed, was found in Plots 4 and 5 at distances 2 m to 10 m. In Plots 2, 3, and 6 some juveniles were randomly distributed and some adults were aggregated. In plot 2, adults were aggregated at 9 to 12 m (Figure 2(b)). Plot 3 juveniles had L(r) values above theoretical random line at radii up to 6.5 meters, exhibiting random and aggregated patterns over the range (Figure 3(c)). The adults, on the other hand, had L(r) values close to the expected values for a randomly distributed population. Plot 6 juveniles exhibited L(r) values greater than expected L(r) values at 1 to 12 m (Figure 3(f)).
The total palm population exhibited a spatially random distribution in three plots and an aggregated distribution in the other three plots (Figure 1). A consistent shift from aggregated juveniles to less aggregated adults was found among all six plots. The shift among juveniles and
 (a)
(a)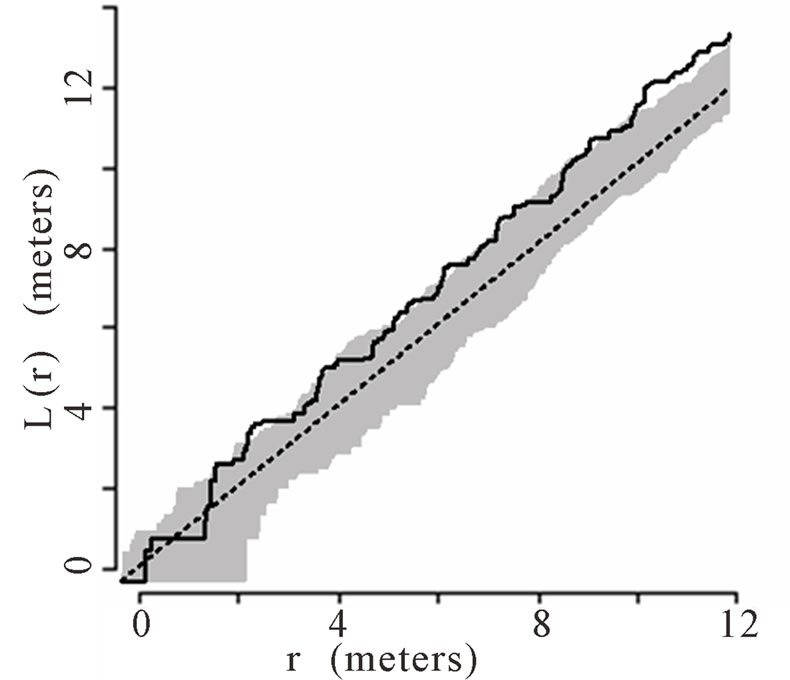 (b)
(b)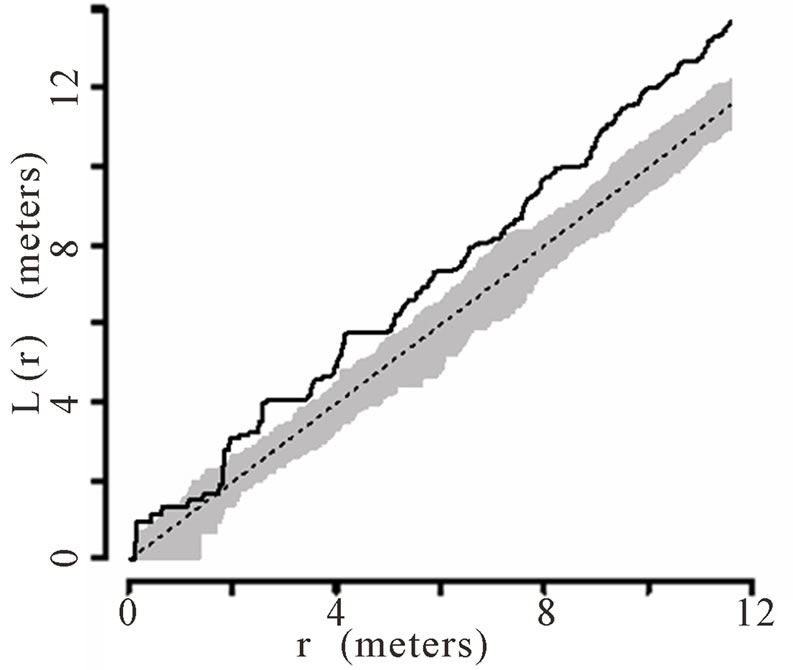 (c)
(c)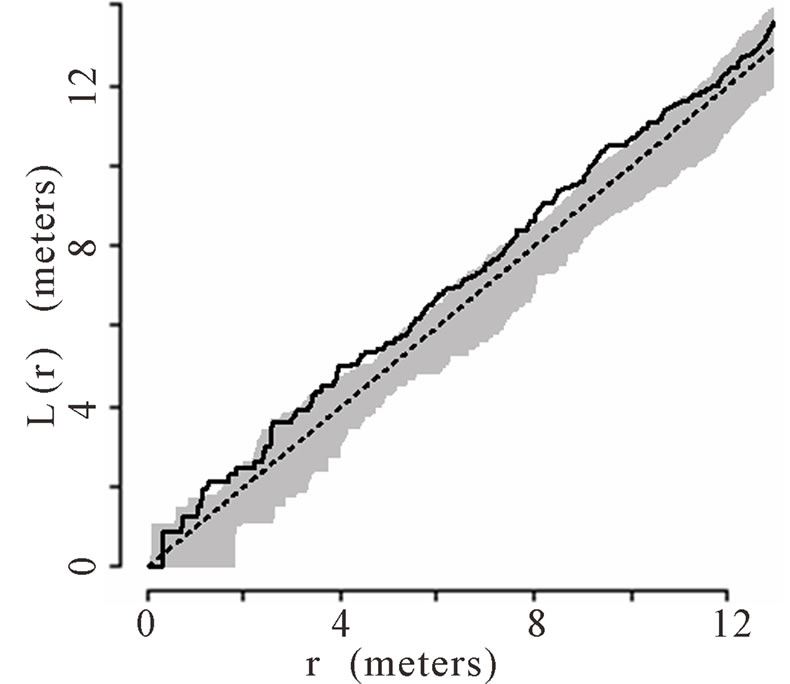 (d)
(d)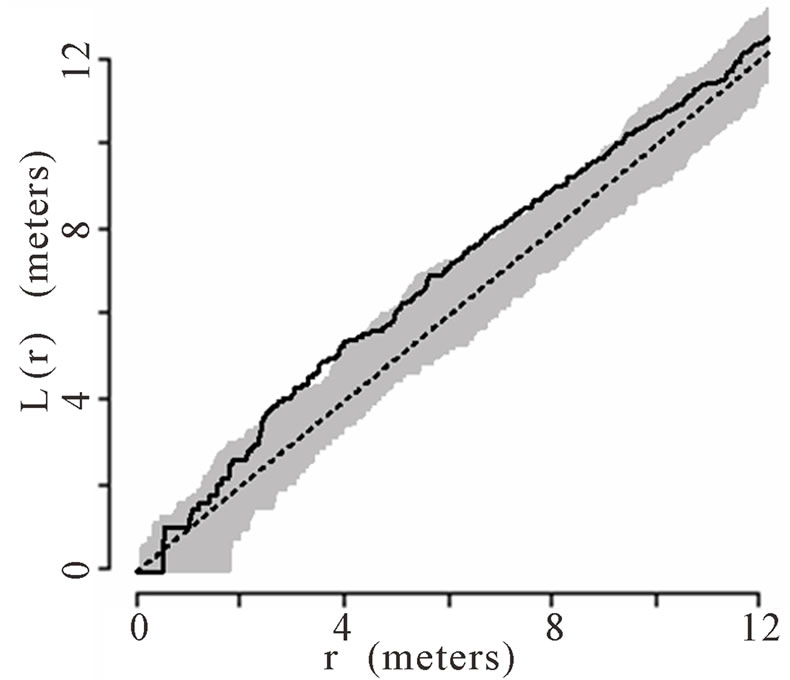 (e)
(e) (f)
(f)
Figure 1. (a)-(f) for Plots 1 - 6 respectively. Transformed Ripley’s K function, L(r), with dashed line indicating theoretical complete spatial randomness and solid line indicating calculated L(r) for all palm trees in each plot. Shaded area represents the 95% confidence envelope. When the calculated L(r) is within the confidence envelope the palms are randomly distributed. When the calculated L(r) is above the confidence envelope the palms are aggregated. When the calculated L(r) is below the confidence envelope the palms are dispersed.
 (a)
(a)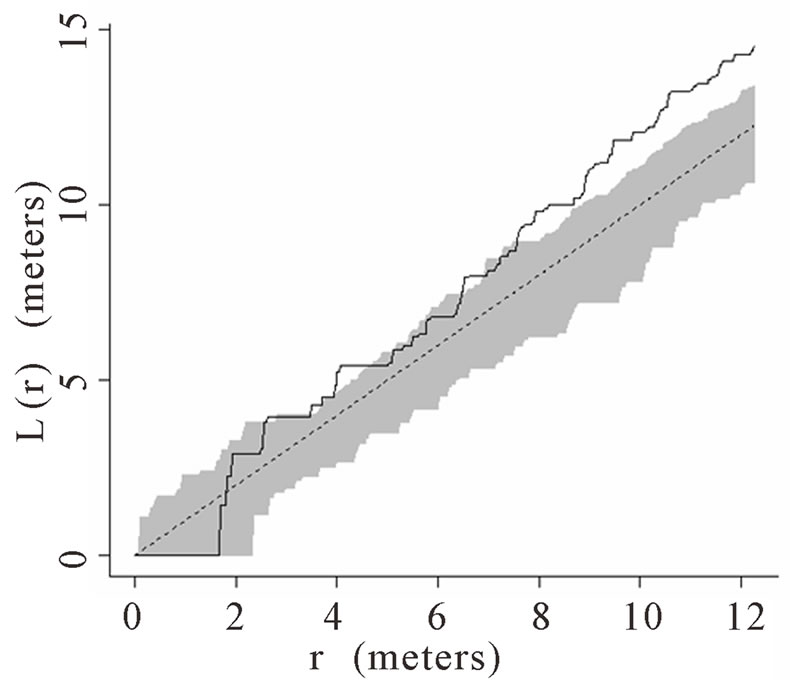 (b)
(b) (c)
(c)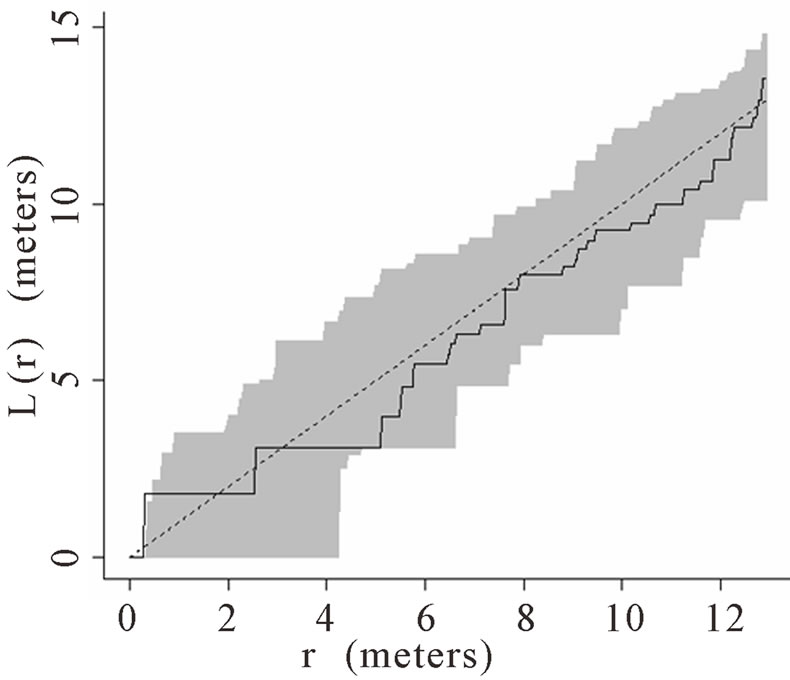 (d)
(d)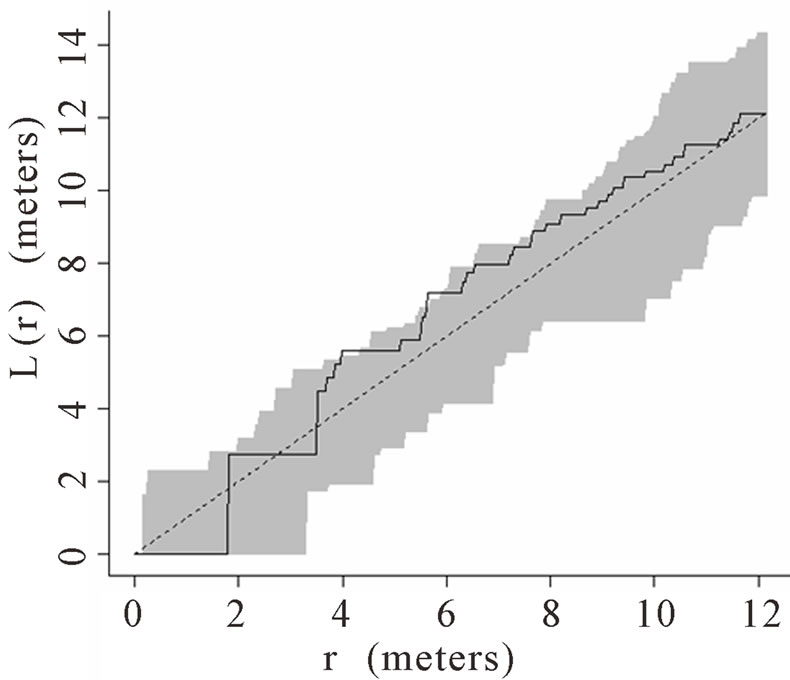 (e)
(e) (f)
(f)
Figure 2. (a)-(f) for Plots 1 - 6 respectively. Transformed Ripley’s K function, L(r), with dashed line indicating theoretical complete spatial randomness and solid line indicating calculated L(r) for adult palm trees in each plot. Shaded area represents the 95% confidence envelope. When the calculated L(r) is within the confidence envelope the palms are randomly distributed. When the calculated L(r) is above the confidence envelope the palms are aggregated. When the calculated L(r) is below the confidence envelope the palms are dispersed.
adults populations was found despite differences in density, juvenile:adult ratios (Table 1) and the resulting structure among plots.
4. Discussion
Our comparison of total palms and then the palm population disaggregated into juvenile and adult populations indicates that aggregation patterns may change for different age cohorts within a stand. The shift from aggregated juvenile populations to less aggregated adult populations has also been found in other palm species, both in savanna and montane rain forests [1,26], in other tree species [13,20,23,25,67] and dominant shrubs [68]. However, other studies have used either adults [4,29] or different life stages but confounded by environmental heterogeneity [1] or the interaction with other species [13,29,32]. Pillay and Ward [34] also surveyed both juveniles and adults, although of woody semi-arid species, and found both juveniles and adults were aggregated. Our study avoided confounding aspects of topography and stand heterogeneity. Its location also contributed to an understanding of the Chaco, a relatively poorly studied and underappreciated environment.
Studies suggest that younger or juvenile plants tend to aggregate [6,32,34]. Aggregation within juvenile populations and random distribution among adults could be a product of intraspecific and inter-specific competition. As juveniles compete for resources with other young palms in small areas, higher rates of mortality may result. Water availability and soil nutrients can be important in driving spatial plant patterns [1,15,69]. Small scale juvenile aggregation could also reflect limited seed dispersal [1,13,21,25,26,28,70]. Wind patterns can determine the distance and direction of seed dispersal. Likewise, small rodents, bats, and birds distribute seeds at varying distances, altering spatial patterns [4,71]. As with other studies we find that aggregation varies with scale [5, 6,34].
5. Conclusions
Using the transformed Ripley’s K function we observed a consistent pattern of aggregation in younger palms to a more spatially random pattern among adult palms. Our study site eliminated both competing dominant species and topographical variation as confounding elements in the study. The exploratory nature of the study did not
 (a)
(a)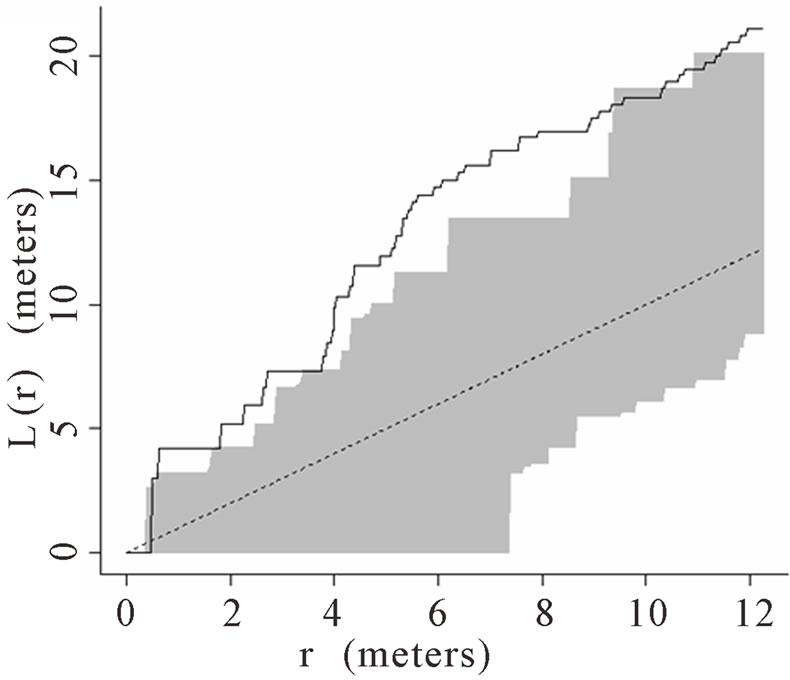 (b)
(b)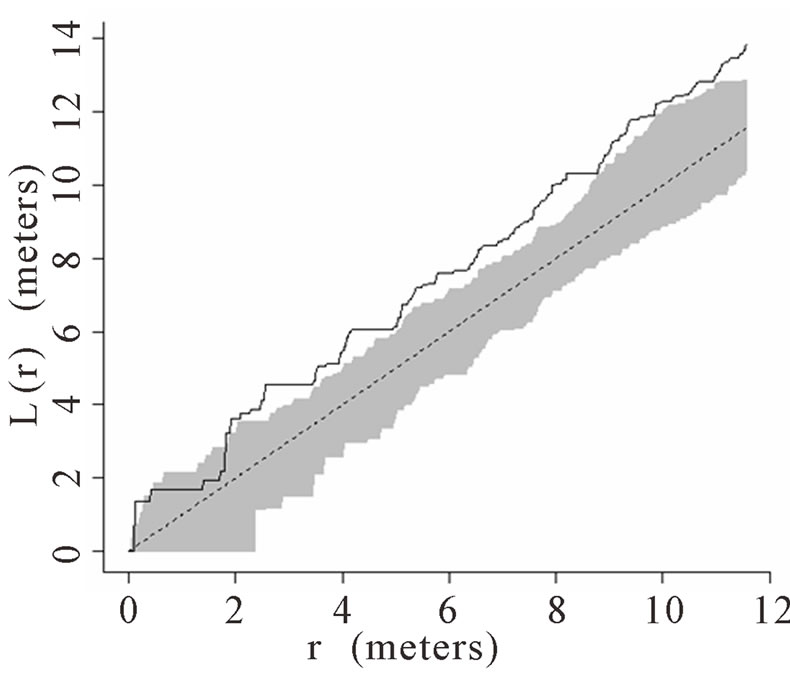 (c)
(c)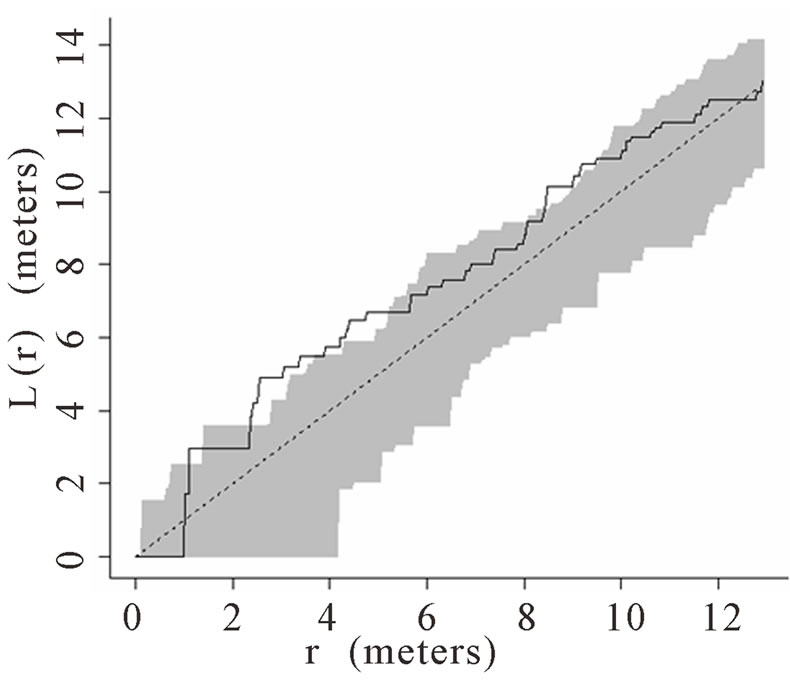 (d)
(d) (e)
(e)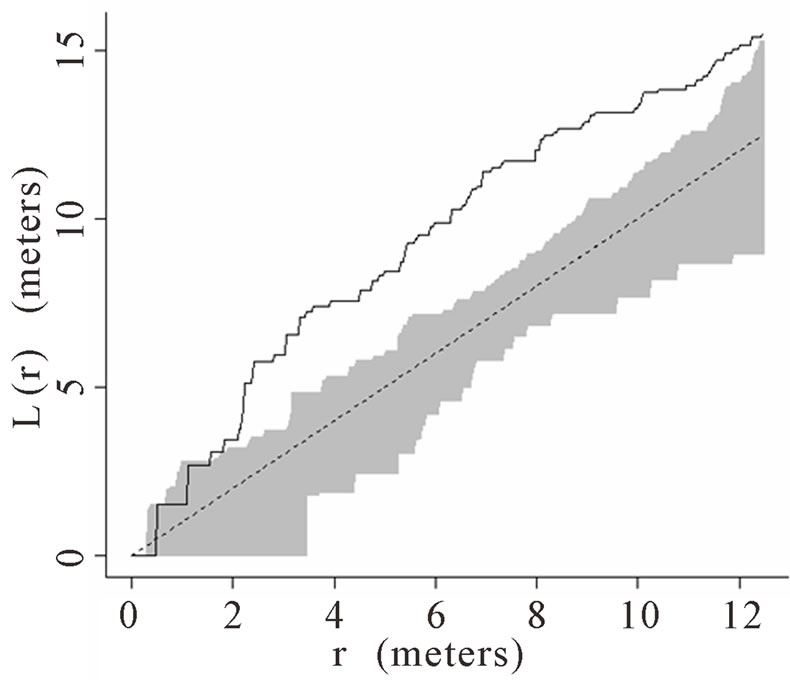 (f)
(f)
Figure 3. (a)-(f) for Plots 1 - 6 respectively. Transformed Ripley’s K function, L(r), with dashed line indicating theoretical complete spatial randomness and solid line indicating calculated L(r) for juvenile palm trees in each plot. Shaded area represents the 95% confidence envelope. When the calculated L(r) is within the confidence envelope the palms are randomly distributed. When the calculated L(r) is above the confidence envelope the palms are aggregated. When the calculated L(r) is below the confidence envelope the palms are dispersed.
allow us to determine underlying ecological drivers for the change in patterns. Future studies addressing the influence of fire, limited nutrient and water resources, and seed dispersal could help understand the mechanisms causing juveniles to aggregate and adults to be more randomly distributed. Long-term studies could lead to an understanding of palm savanna succession and how the plant communities are changing in response to fire and current climatic conditions.
6. Acknowledgements
We thank Gustavo Arévalos, Heather Clark, Rosa Degen, Luis Jiménez, Miguel Navarro, Sarah Page, Joan Ngo, and Brad Vanderford for their assistance in collecting data, curating plant specimens, and preparing the manuscript.
REFERENCES
- S. Barot, J. Gignoux and J.-C. Menaut, “Demography of a Savanna Palm Tree: Predictions from Comprehensive Spatial Pattern Analyses,” Ecology, Vol. 80, No. 6, 1999, pp. 1987-2005. doi:10.1890/0012-9658(1999)080[1987:DOASPT]2.0.CO;210.1890/0012-9658(1999)080[1987:DOASPT]2.0.CO;2
- D. W. Goodall, “Quantitative Aspects of Plant Distribution,” Biological Reviews of the Cambridge Philosophical Society, Vol. 27, No. 2, 1952, pp. 194-245. doi:10.1111/j.1469-185X.1952.tb01393.x
- J. G. Skellam, “Studies in Statistical Ecology: I. Spatial Patterns,” Biometrika, Vol. 39, No. 3-4, 1952, pp. 346- 362.
- L. B. de Almeida and M. Galetti, “Seed Dispersal and Spatial Distribution of Attalea geraensis (Arecaceae) in Two Remnants of Cerrado in Southeastern Brazil,” Acta Oecologia, Vol. 32, No. 2, 2007, pp. 180-187. doi:10.1016/j.actao.2007.04.001
- A. P. Rayburn, K. Schiffers and E. W. Schupp, “Use of Precise Spatial Data for Describing Spatial Patterns and Plant Interactions in a Diverse Great Basin Shrub Community,” Plant Ecology, Vol. 212, No. 4, 2011, pp. 585- 594. doi:10.1007/s11258-010-9848-0
- C. Armas and F. I. Pugnaire, “Plant Interactions Govern Population Dynamics in a Semi-Arid Plant Community,” Journal of Ecology, Vol. 93, No. 5, 2005, pp. 978-989. doi:10.1111/j.1365-2745.2005.01033.x
- P. Stoll and E. Bergius, “Pattern and Process: Competition Causes Regular Spacing of Individuals within Plant Populations,” Journal of Ecology, Vol. 93, No. 2, 2005, pp. 395-403. doi:10.1111/j.0022-0477.2005.00989.x
- E. J. B. McIntire and A. Fajardo, “The Active and Effective Way to Infer Processes from Spatial Patterns,” Ecology, Vol. 90, No. 1, 2009, pp. 46-56. doi:10.1890/07-2096.1
- J. Choo, T. E. Juenger and B. B. Simpson, “Consequences of Frugivore-Mediated Seed Dispersal for the Spatial and Genetic Structures of a Neotropical Palm,” Molecular Ecology, Vol. 21, No. 4, 2012, pp. 1019-1031. doi:10.1111/j.1365-294X.2011.05425.x
- T. A. Scanlon, K. K. Caylor, S. A. Levin and I. Rodriguez-Iturbe, “Positive Feedbacks Promote Power-Law Clustering of Kalahari Vegetation,” Nature, Vol. 449, No. 7159, 2007, pp. 209-212. doi:10.1038/nature06060
- A. F. Souza and F. R. Martins, “Population Structure and Dynamics of a Neotropical Palm in Fire-Impacted Fragments of the Brazilian Atlantic Forest,” Biodiversity and Conservation, Vol. 13, No. 9, 2004, pp.1611-1632. doi:10.1023/B:BIOC.0000029326.44647.7f
- P. Greig-Smith and M. J. Chadwick, “Data on Pattern within Plant Communities: III Acacia-Capparis Semi-Desert Scrub in the Sudan,” Journal of Ecology, Vol. 53, No. 2, 1965, pp. 465-474. doi:10.2307/2257989
- F. He, P. Legendre and J. V. LaFrankie, “Distribution Patterns of Tree Species in a Malaysian Tropical Rain Forest,” Journal Vegetation Science, Vol. 8, No. 1, 1997, pp. 105-114. doi:10.2307/3237248
- F. Jeltsch, S. J. Milton, W. R. J. Deans and N. Van Rooyen, “Tree Spacing and Coexistence in Semiarid Savannas,” Journal of Ecology, Vol. 84, No. 4, 1996, pp. 583-595. doi:10.2307/2261480
- J.-C. Svenning, “On the Role of Microenvironmental Heterogeneity in the Ecology and Diversification of Neotropical Rain-Forest Palms (Arecaceae),” The Botanical Review, Vol. 67, No. 1, 2001, pp. 1-53. doi:10.1007/BF02857848
- M. Lieberman, D. Lieberman, G. S. Hartshorn and R. Peralta, “Small-Scale Altitudinal Variation in Lowland Wet Tropical Forest Vegetation,” Journal of Ecology, Vol. 73, No. 2, 1985, pp. 505-516. doi:10.2307/2260490
- J.-C. Svenning, D. Harlev, M. M. Sorensen and H. Balslev, “Topographic and Spatial Controls of Palm Species Distributions in a Montane Rain Forest, Southern Ecuador,” Biodiversity and Conservation,” Vol. 18, No. 1, 2009, pp. 219-228. doi:10.1007/s10531-008-9468-3
- N. C. Kenkel, “Pattern of Self-Thinning in Jack Pine; Testing the Random Mortality Hypothesis,” Ecology, Vol. 69, No. 4, 1988, pp. 1017-1024. doi:10.2307/1941257
- P. Haase, F. I. Pugnaire, S. C. Clark and L. D. Incoll, “Spatial Patterns in a Two-Tiered Semi-Arid Shrubland in South-Eastern Spain,” Journal of Vegetation Science, Vol. 7, No. 4, 1996, pp. 527-534. doi:10.2307/3236301
- K. Wiegand, F. Jeltsch and D. Ward, “Do Spatial Effects Play a Role in the Spatial Distribution of Desert-Dwelling Acacia raddiana?” Journal of Vegetation Science, Vol. 11, No. 4, 2000, pp. 473-484. doi:10.2307/3246577
- T. Wiegand, S. Gunatilleke, N. Gunatilleke and T. Okuda, “Analyzing the Spatial Structure of a Sri Lankan Tree Species with Multiple Scales of Clustering,” Ecology, Vol. 88, No. 12, 2007, pp. 3088-3102. doi:10.1890/06-1350.1
- S. Getzin, C. Dean, F. He, J. A. Trofymow, K. Wiegand and T. Wiegand, “Spatial Patterns and Competition of Tree Species in a Douglas-fir Chronosequence on Vancouver Island,” Ecogeography, Vol. 29, No. 5, 2006, pp. 671-682. doi:10.1111/j.2006.0906-7590.04675.x
- R. W. Sterner, C. A. Ribic and G. E. Schatz, “Testing for Life Historical Changes in Spatial Patterns of 4 Tropical Tree Species,” Journal of Ecology, Vol. 74, No. 3, 1986, pp. 621-633. doi:10.2307/2260386
- J. M. V. Fragoso, “Tapir-Generated Seed Shadows: Scale-Dependent Patchiness in the Amazon Rain Forest,” Journal of Ecology, Vol. 85, No. 4, 1997. pp. 519-529. doi:10.2307/2960574
- J. B. Plotkin, M. D. Pott, N. Leslie, N. Manokaran, J. LaFrankie and P. S. Ashton, “Species-Area Curves, Spatial Aggregation, and Habitat Specialization in Tropical Forest,” Journal of Theoretical Biology, Vol. 207, No. 1, 2000, pp. 81-99. doi:10.1006/jtbi.2000.2158
- J.-C. Svenning, “Environmental Heterogeneity, Recruitment Limitation and the Mesoscale Distribution of Palms in a Tropical Montane Rain Forest (Maquipucuna, Ecuador),” Journal of Tropical Ecology, Vol. 17, No. 1, 2001. pp. 97-113. doi:10.1017/S0266467401001067
- A. C. Cabral, “Shrub Encroachment in Argentinean Savannas,” Journal of Vegetation Science, Vol. 14, No. 2, 2003, pp. 145-152. doi:10.1111/j.1654-1103.2003.tb02139.x
- E. C. Pielou, “The Use of Plant-to-Neighbour Distances for the Detection of Competition,” Journal of Ecology, Vol. 50, No. 2, 1962, pp. 357-367. doi:10.2307/2257448
- D. B. Clark, D. A. Clark and J. M. Read, “Edaphic Variation and the Mesoscale Distribution of Tree Species in a Neotropical Rain Forest,” Journal of Ecology, Vol. 86, No. 1, 1998, pp. 101-112. doi:10.1046/j.1365-2745.1998.00238.x
- K. Mokany, J. Ash and S. Roxburgh, “Effects of Spatial Aggregation on Competition, Complementarity, and Resource Use,” Austral Ecology, Vol. 33, No. 3, 2008, pp. 261-270. doi:10.1111/j.1442-9993.2007.01813.x
- G. L. W. Perry, N. J. Enright, B. P. Miller and B. B. Lamont, “Nearest-Neighbor Interactions in Species-Rich Shrublands: The Roles of Abundance, Spatial Patterns and Resources,” Oikos, Vol. 118, No. 2, 2009, pp. 161-174. doi:10.1111/j.1600-0706.2008.16947.x
- E. S. Lima, J. M. Felfili, and B. S. Marimon e Aldicir Scariot, “Diversidade, Estrutura, e Distribuicao Especial de Palmeiras em um Cerrado sensu stricto no Brasil Central-DF,” Revista Brasileira de Botanica, Vol. 26, No. 3, 2003, pp. 361-370. doi:10.1590/S0100-84042003000300009
- R. Condit, P. S. Ashton, P. Baker, S. Bunyavejchewin, S. Gunatilleke, et al., “Spatial Patterns in the Distribution of Tropical Tree Species,” Science, Vol. 288, No. 5470, 2000, pp. 1414-1418. doi:10.1126/science.288.5470.1414
- T. Pillay and D. Ward, “Spatial Pattern Analysis and Competition between ACACIA karroo Trees in Humid Savannas,” Plant Ecology, Vol. 213, No. 10, 2012, pp. 1609-1619. doi:10.1007/s11258-012-0115-4
- S. Hamilton, “Hydrological Controls of Ecological Structure and Function in the Pantanal Wetland (Brazil),” In: M. E. McClain, Ed., Ecohydrology of South American Rivers and Wetlands. No. 6 IAHS Special Publication, IAHS Press, Wallingford, 2002, pp. 133-156
- G. Navarro, J. A. Molina and S. Vega, “Soil Factors Determining the Change in Forests between Dry and Wet Chacos,” Flora—Morphology, Distribution, Functional Ecology of Plants, Vol. 206, No. 2, 2011, pp. 136-143. doi:10.1016/j.flora.2010.09.002
- G. Prance and G. B. Schaller, “Preliminary Study of Some Vegetation Types of the Pantanal, Mato Grosso, Brazil,” Brittonia, Vol. 34, No. 2, 1982, pp. 228-251. doi:10.2307/2806383
- S. Bravo, C. Kunst and R. Grau, “Suitability of the Native Woody Species of the Chaco Region, Argentina, for Use in Dendroecological Studies of Fire Regimes,” Dendrochronologia, Vol. 26, No. 1, 2008, pp. 43-52. doi:10.1016/j.dendro.2007.05.004
- J. E. Hay, “Tobati: Tradition and Change in a Paraguayan Town,” Ph.D. Dissertation, University of Florida, Gainesville, 1993.
- M. Iriondo, “Geomorphology and Late Quaternary of the Chaco (South America),” Geomorphology, Vol. 7, No. 4, 1993, pp. 289-303. doi:10.1016/0169-555X(93)90059-B
- S. Gardner, M. R. Cabido, G. R. Valladares and S. Diaz, “The Influence of Habitat Structure on Arthropod Diversity in Argentine Semi-Arid Chaco Forest,” Journal of Vegetation Science, Vol. 6, No. , 1995, pp. 349-356. doi:10.2307/3236234
- P. B. Raimundo and J. D. Hay, “Patterns and Dynamics of Plant Populations,” In: P. S. Oliveira and R. J. Marquis, Eds., The Cerrados of Brazil. Ecology and Natural History of a Neotropical Savanna, Columbia University Press, New York, 2002, pp. 140-158.
- A. Pott and V. A. Pott, “Features and Conservation of the Brazilian Pantanal Wetland,” Wetlands Ecology and Management, Vol. 12, No. 6, 2004, pp. 547-552. doi:10.1007/s11273-005-1754-1
- F. Riveros, “The Gran Chaco,” 2010. http://www.fao.org/ag/AGP/AGPC/doc/Bulletin/Granchaco.htm
- DMH (Direccion de Meteorologia e Hidrologia), Monthly Climate Bulletin, Gerencia de Climatología e Hidrología, 2011. http://www.meteorologia.gov.py/climatologia/bolmensual.pdf
- F. Mereles, “Estudios Cuantitativos en las Sabanas de ‘Karandá’y’, Copernicia alba Morong, en el Chaco Boreal y la Sub-cuenca del lago Ypacarai, Paraguay,” Rojasiana, Vol. 5, No. 2, 2001, pp. 279-290.
- TuTiempo World Weather, “Wind Velocity Data of Corumbá, Brasil,” 2011. www.tutiempo.net/clima/Corumba/01
- H. M. Valente, “Estudio Quimico de la Madera de Palma, Copernicia alba, Morong,” Revista de Investigaciones Forestales, Vol. 1, No. 4, 1957, pp. 53-61.
- B. E. Dahlgren and S. F. Glassman, “A Revision of the Genus Copernicia,” Gentes Herbarium, Vol. 9, No. 1, 1963, pp. 1-40.
- J. A. López, J. A. E. L. Little, G. F. Ritz, J. S. Rombold and W. J. Hanh, “Árboles Comunes del Paraguay. Ñande Yvyra Mata Kuera,” Cuerpo de Paz Colección e Intercambio de Información. Asuncion, 1987.
- J. J. Neiff, “Diversity in Some Tropical Wetland Systems of South America,” In: B. Gopal, W. J. Junk and J. A. Davis, Eds., Biodiversity in Wetlands: Assessment, Function and Conservation, Backhuys Publishers, Leiden, 2001, pp. 157-186.
- J. D. Johnson, “The Raposa palm plantation revisited,” Principes, Vol. 25, No. 3, 1981, 133-139.
- M. Moraes, “Contribución al Estudio del ciclo Biologico de la Palma Copernicia Alba en un Area Ganadera (Espiritu, Beni, Bolivia),” Ecología en Bolivia, Vol. 18, 1991, pp. 1-22.
- F. Mereles, “Aspectos Fenologicos de la Vegetacion Herbacea de los Palmares de Copernicia alba del Chaco Boreal, Paraguay,” Rojasiana, Vol. 5, No. 1, 1999, pp. 67- 99.
- M. Schessl, “[3448] The New York Botanical Gardens Virtual Herbarium,” 1993. http://sweetgum.nybg.org/vh/specimen.php?irn=945324/
- A. Orozco-Segovia, A. I. Batis, M. Rojas-Arechiga and A. Mendoza, “Seed Biology of Palms: A Review,” Palms, Vol. 47, No. 2, 2003, pp. 79-84.
- A. Keuroghlian, D. P. Eaton and A. J. Desbiez, “The Response of a Landscape Species, White-Lipped Peccaries, to Seasonal Resource Fluctuations in a Tropical Wetland, the Brazilian Pantanal,” International Journal of Biodiversity and Conservation, Vol. 1, No. 4, 2009, pp. 87-97.
- D. H. Janzen, “Herbivores and the Number of Tree Species in Tropical Forests,” The American Naturalist, Vol. 104, No. 940, 1970, pp. 501-528. doi:10.1086/282687
- R. Degen, “Dinámica Poblacional del Copernicia alba Morong Caranda’y. Dirección de Ordenamiento Ambiental and Estación Experimental Chaco Central. Final Report,” Paraguayan Technical Cooperation-Germany, Ministry of Agriculture (GTZ), Asuncion, 1998.
- C. Yamashita and Y. M. Barros, “The Blue-Throated Macaw Ara glaucogularis: Characterization of Its Distinctive Habitats in Savannahs of the Beni, Bolivia,” Ararajuba, Vol. 5, No. 2, 1997, pp. 141-150.
- C. F. Vogt and F. Mereles, “Una Contribución al Estudio de los Humedales de la Cuenca del Arroyo Ñeembucú, Departmento Ñeembucú, Paraguay,” Rojasiana, Vol. 7, No. 1, 2005, pp. 5-20.
- D. Stoyan and A. Penttinen, “Recent Applications of Point Process Methods in Forest Statistics,” Statistical Science, Vol. 15, No. 1, 2000, pp. 61-78.
- A. Baddeley and R. Turner, “Spatstat: An R Package for Analyzing Spatial Point Patterns,” Journal of Statistical Software, Vol. 12, No. 6, 2005, pp. 1-42.
- R Development Core Team, R Foundation for Statistical Computing, Vienna, Austria, “R: A Language and Environment for Statistical Computing,” 2010. http://www.R-project.org/
- M. Cisz, “The Spatial Distribution of Copernicia alba in the District of Bahía Negra, Paraguay,” M.S. Thesis, Michigan Technological University, Houghton, 2011.
- B. D. Ripley, “Spatial Statistics,” John Wiley Sons, New York, 1981. doi:10.1002/0471725218
- E. C. Pielou, “A Single Mechanism to Account for Regular, Random, and Aggrgated Populations,” Journal of Ecology, Vol. 48, No. 3, 1960, pp. 575-584. doi:10.2307/2257334
- D. Gibson and E. Menges, “Population Structure and Spatial Pattern in the Dioecious Shrub,” Journal of Vegetation Science, Vol. 5, No. 3, 1994, pp. 337-346. doi:10.2307/3235857
- P. Greig-Smith, “Pattern in Vegetation,” Journal of Ecology, Vol. 67, No. 3, 1979, pp. 755-779. doi:10.2307/2259213
- J. Antonovics and R. B. Primack, “The Ecological and Genetic Consequences of Density-Dependent Regulation in Plants,” Annual Review of Ecology and Systematics, Vol. 11, 1980, pp. 411-452. doi:10.1146/annurev.es.11.110180.002211
- E. V. Wehncke, X. L. Medellin and E. Ezcurra, “ Patterns of Frugivory, Seed Dispersal and Predation of Blue Fan Palms (Brahea armata) in Oases of Northern Baja California,” Journal of Arid Environments, Vol. 73, No. 9, 2009, pp. 773-783. doi:10.1016/j.jaridenv.2009.03.007
NOTES
*Corresponding author.

