Received 24 January 2015; accepted 15 February 2015; published 16 February 2015

ABSTRACT

In this paper, we derive and analyse rigorously a mathematical model of control strategies (scree- ning, education, health care and immunization) of HCV in a community with inflow of infected immigrants. Both qualitative and quantitative analysis of the model is performed with respect to stability of the disease free and endemic equilibria. The results show that the disease free equilibrium is locally stable at threshold parameter less than unity and unstable at threshold parameter greater than unity. Using Lyapunov method, endemic equilibrium is globally stable under certain conditions. Numerical simulation of the model is implemented to investigate the sensitivity of certain key parameters on the HCV model in a community with inflow of infected immigrants. However, analysis shows that screening, education, health care and immunization have the effect of reducing the transmission of the disease in the community.

Keywords:

HCV Disease, Infected Immigrants, Stability, Sensitivity Index, Lyapunov Method, Screening, Education, Health Care and Immunization

1. Introduction

Hepatitis C is a blood borne liver disease, caused by the Hepatitis C Virus (HCV), first identified by [1] . Moreover, the link between infectious diseases and screening must be understood in relation to infectives on the spread of HCV infections. [2] analysed the screening of HCV in a health maintenance Organization. Mathematical modelling of the spread of infectious diseases continues to become an important tool in understanding the dynamics of diseases and in decision making processes regarding diseases intervention programs for disease in many countries. For instance, [3] formulated and analysed a mathematical model on the effect of Treatment and Infected Immigrants on the spread of Hepatitis C Virus disease at Acute and Chronic stages. [4] considered SEI (Susceptible-Exposed-Infective) epidemic model with acute and chronic stages. [5] investigated the effects of a HCV educational intervention or a motivational intervention on alcohol use and sexual risk behaviours among injection drug users. [6] studied the potential impact of vaccination on the hep C virus epidemic in injection drug users. [7] presented the study on immunization strategies in chronic HCV infection. [8] reported that HCV patient education is associated with positive outcomes in various models of HCV care. However, in all the above studies, none of them incorporated the HCV infectiology and control strategies (screening, education, health care and immunization) in a community with inflow of infected immigrants. The aim of the paper is to have a deeper understanding of the effects of screening, education, health care and immunization in controlling the spread of HCV.

2. Model Formulation

A mathematical model is proposed and analysed to study the effect of screening, education, health care and immunization on the spread of HCV disease in the community. The model has five epidemiological classes: The susceptible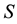, exposed individuals, the acute Infectives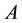, the chronic infectives and recovered group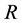. Total population at time is given by:

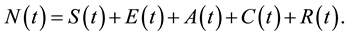(1)

The interaction between the classes is being assumed as follows: Exposed individuals, acute infected and chronic infected immigrants enter into the population with the rates 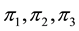respectively. Susceptible individuals are infected with the HCV virus at a rate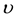, where 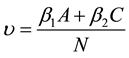and 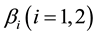are effective contact rate of individuals with acute and chronic hepatitis C respectively. It is assumed that the rate of contact of susceptibles with chronic individuals is much less than that of acute infectives because at chronic stage, people become aware of their infection and may choose to use control measures and change their behaviour and thus may contribute little in spreading the infection. The control variable based on screening programme aimed at, reduces the inflow of infected immigrants into the community at the rate 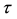and is the control variable based on education, health care and immunization to decrease the infection contact rate.

Taking into account the above considerations, we then have the following schematic flow diagram (Figure 1):

From the above flow chart, and with

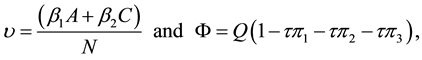
the model will be governed by the following system of equations:

(2)

with nonnegative initial conditions and.

where

are the effective contact rates of individuals with acute and HCV respectively,

are the rates at which exposed, acute and Chronic infected immigrants enter into the population respectively,

is the recruitment rate,

is the rate of progression to acute infected class from exposed class,

are the rates at which acute and exposed infective develop chronic respectively,

are the rates at which acute and chronic individuals recovered respectively,

is the death rate of acute infected group due to the disease,

is the rate at which infectious humans after recovery become immediately susceptible again,

is the natural death rate,

is the death rate of chronic infected group due to the disease,

is the screening rate of infected immigrants.

3. Model Analysis

The model system of Equations (2) will be analysed qualitatively to get insight into its dynamical features which will give a better understanding of the effects of screening, education, health care and immunization on the transmission of HCV infection in the population with inflow of infected immigrants. The threshold which governs elimination or persistence of HCV will be determined and studied. We begin by finding the invariant region and show that all solutions of system (2) are positive.

3.1. Invariant Region

In this section, a region in which solutions of the model system (2) are uniformly bounded is the proper subset

Let be any solution with positive initial conditions. Then from Equation (2) it is noted that in the absence of the disease related mortality (i.e.), the rate of change of the population is given by,

(3)

Using Birkhoff and Rota’s theorem [9] on the differential inequality (3), the following expression is obtained;

(4)

where is the value evaluated at the initial conditions of the respective variables.

Thus, as in (4), the population size, , which implies that In respectof this, all the feasible solutions of system (2) enter the region.

Hence, is positively invariant and it issufficient to consider solutions in.

Furthermore, existence, uniqueness and continuation of results for system (2) hold in this region.

Lemma 1: The region is positively invariant for the model system (2) with initial conditions in.

3.2. Positivity of Solutions

Lemma 2: Let the initial data be then, the solution set of the system (2) is positive

Proof:

From the first equation of the model system (2), we have

The Integration factor is, multiplying both sides by the integration factor and integrating leads to

Equations for can be similarly be obtained.

Thus are positive.

3.3. The Disease Free Equilibrium Point (DFE)

In the absence of the disease, which implies that the disease free equilibrium points is given by

3.4. The Effective Reproductive Number R_e

In this section, the threshold parameter that governs the spread of a disease which is called the effective reproduction number is determined. Mathematically, it is the spectral radius of the next generation matrix [10] .

This definition is given for the models that represent spread of infection in a population. It is obtained by taking the largest (dominant) Eigen value, (spectral radius) of

(5)

where is the rate of appearance of new infection in compartment, is the transfer of individuals out of the compartment by all other means and is the disease free equilibrium.

Therefore,

(6)

and

(7)

The partial derivatives if (6) and (7) with respect to gives

(8)

and

(9)

In the absence of the disease and when, the matrix (8) becomes

(10)

Now, taking the inverse of matrix (9) leads to

(11)

where

The spectral radius (dominant eigenvalue) of the matrix is

Hence, the effective reproduction number of the model system (2) is given by

(12)

The effective reproduction number measures the average number of new infections generated by a typical infectious individual in a community with inflow of infected immigrants when screening, education, health care and immunization strategies are in place.

Theorem 1: The disease free equilibrium of the model system (2) is locally asymptotically stable if and unstable if.

Theorem 1 implies that HCV can be eliminated from the community when if the initial size of the sub population of the model are in the basin of attraction of the disease free equilibrium. That means if, then on average an infected individual produce less than one new infected individual over the course of its infectious period and the infection cannot grow.

From Equation (12), for to be less than 1 this will only be possible when (which implies HCV education, health care and immunization) are increased without bound in collaboration with other intervention strategies to all people including immigrants in a given locality which may result into the decreasing effect on.

In the absence of interventions (screening, education, health care and immunization) that is, is reduced to:

Thus. Hence the presence of screening, education, health care and immunization can eradicate the HCV infection if can be reduced to below unity.

3.5. Local Stability of Disease Free Equilibrium (DFE)

Local stability of disease free equilibrium, can be determined by the variational matrix of the model system (2). The Jacobian matrix at the steady states is given by;

(13)

The local stability analysis of the Jacobian matrix (13) of the system (2) can be done by the trace/determinant method. Where by matrix is locally asymptotically stable if and only if the trace of matrix is strictly negative and its determinant is strictly positive. Whose trace and determinant are given by

(14)

and

where, , , , ,.

Hence if

That is equivalent to

since

Thus, is locally asymptotically stable if and only if. These results are summarized with the theorem 1.

3.6. The Endemic Equilibrium Point D

Endemic equilibrium point is a steady state solution in which the disease persists in the population (i.e.)

(15)

where,

and is the solution of the quadratic polynomial

(16)

where,

The equation, corresponds to a situation when the disease persists (endemic). In case of backward bifurcation, multiple endemic equilibrium must exist.

However it is important to note that is always positive if and negative if.

Theorem 2: The HCV model with screening, education, health care and immunization interventions have:

i) Precisely one unique endemic equilibrium if

ii) Precisely one unique endemic equilibrium if and or

iii) Precisely two endemic equilibrium if, and.

iv) None otherwise.

Theorem 3: A unique endemic equilibrium point, exists if and only if.

3.7. Global Stability of the Endemic Equilibrium Point D

The global stability of the endemic equilibrium is analysed using the following constructed Lyapunov function by [11]

Theorem 4: If, the endemic equilibrium of the model (2) is globally asymptotically stable.

Proof: To establish the global stability of the endemic equilibrium, we construct the following Lyapunov function:

By direct calculating the derivative of along the solution of (2) we have;

or

(17)

where,

Thus if then; Noting that if and only if;;;;: Therefore, the largest compact invariant set in is the singleton where is the endemic equilibrium of the system (2). By LaSalle’s invariant principle, it implies that is globally asymptotically stable in if .

3.8. Numerical Sensitivity Analysis

In determining how best to reduce human mortality and morbidity due to HCV, we calculate the sensitivity indices of the basic reproduction number, to the parameters in the model using approach of [12] . These indices are crucial in determining the importance of each individual parameter in transmission dynamics and prevalence of the disease. Sensitivity analysis determines parameters that have a high impact on and should be targeted by intervention strategies. Sensitivity indices allow us to measure the relative change in a state variablewhen a parameter changes [12] . When a variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives.

Numerical values of sensitivity indices of to parameter values for the HCV model, evaluated using the following estimated parameter values:, , , , , , , , , and.

Definition 1: The normalised forward sensitivity index of a variable “” that depends differentiable on a parameter “” is defined as:

(18)

Having an explicit formula for in Equation (18), we derive an analytical expression for the sensitivity of

as to each of parameters involved in. For example the sensitivity indices of with

respect to and are given by;

and

Other indices

are obtained following the same method and tabulated as follows:

From Table 1, it can be observed that when the parameters, , and are increased keeping the other parameters constant they increase the value of implying that they increase the endemicity of the dis- ease as they have positive indices. While the parameters, , , , , and decrease the value of when they are increased while keeping the other parameters constant, implying that they decrease the

endemicity of the disease as they have negative indices.

The specific interpretation of each parameter shows that, the most sensitive parameter is the control based on education, health care and immunization, followed by effective contact rate of individuals with chronic disease, then recovered rate of chronic individuals due to treatment, effective contact rate of individuals with acute, followed by recovery rate naturally from acute, death rate of chronic infected, recovered rate of acute individuals due to treatment, natural mortality rate, rate at which exposed develop chronic, the rate at which acute infective are detected by a screening method from exposed group, the rate at which screened develop to chronic, which is the least sensitive parameter.

3.9. Numerical Simulations

In this section, we illustrate the analytical results of the study by carrying out numerical simulations of the model system (2) using the following estimated parameter values:, , , , , , , , , , , , , ,.

Figures 2(a)-(d) show the proportion of HCV exposed, infective populations (acute, chronic) and proportion of HCV infectives all plotted against the proportion of susceptible population. This shows the dynamic beha-

viour of the endemic equilibrium of the model system (2) using the estimated parameter values above.

The phase portrait in Figures 2(a)-(d) shows that for any initial starting point or initial value, the solution curves tend to the endemic equilibrium point. Hence, we infer that the system (2) is globally stable about the endemic equilibrium point for the set of parameters above.

In Figures 3(a)-(d), the variation of proportions of exposed, recovered, acute and chronic infective populations for different rates of education, health care and immunization is shown.

Figures 3(a)-(d), shows that the infected population decreases as the control strategies (education, health care and immunization), increased. This confirms that, if is not effective the disease will invade the population.

Figures 4(a)-(d) shows the variation of proportions of exposed, acute and chronic infective populations and recovered population for different rates of screening.

From Figures 4(a)-(d) we vary the screened rate of infected immigrants, and it is seen that as the degree of screening increases, the infected population decreases. The results further show that increasing the screening rate, decreases the severity of the epidemic. Once again this confirms that, screening can reduce the inflow of infected immigrants into the community.

4. Discussions and Conclusion

In this paper, a mathematical model of control strategies of HCV in a community with inflow of infected immigrants been established. Both qualitative and numerical analysis of the model was done. The model incorporates the assumption that infected immigrants enter in the community. It is shown that there exists a feasible region where the model is well posed in which a unique disease free equilibrium point exists. The disease free and endemic equilibrium points were obtained and their stabilities investigated. The model showed that the disease free equilibrium is locally stable at threshold parameter less than unity and unstable at threshold parameter greater than unity. Using Lyapunov method, endemic equilibrium is globally stable under certain conditions. A sensitivity analysis shows that the control based on education, health care and immunization is the most sensitive parameter on and the least is. A numerical study of the model has been conducted to see the effect of certain key parameters on the spread of the disease. It was observed that the spread of the disease decreases due to the presence of control strategies (screening, education, health care and immunization). As the control strategies increase, the exposed, acute and chronic infective individuals also decrease in the population. Finally, from the analysis, it may be hypothesized that preventive measures, through reducing rates of transmission of HCV are therefore necessary to the community. Since reduced transmission leads to lower prevalence of the disease in the long-term, the national health care to HCV should therefore seek to ensure that all people at risk or that have been at risk in the past, have access to and are supported in the use of HCV screening, education, health care immunization, regardless of their social and economic status.

References

NOTES

^*Corresponding author.