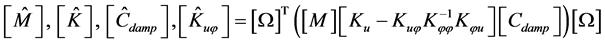Received 6 February 2016; accepted 22 February 2016; published 25 February 2016

ABSTRACT

Active vibration control of functionally graded material (FGM) plate with integrated piezoelectric layers is studied. In this regard, a finite element model based on the classical plate theory is adopted and extended to the case of FGM plate to obtain a space state equation. Rectangular four node and eight node elements are used for the analysis purpose. The material proprieties of FG plate are assumed to be graded along the thickness direction. In order to control the vibration of the plate, an LQR controller has been designed and developed. The weighing factors are obtained by using genetic algorithm. The proposed results of finite element modeling are verified with the results obtained using ANSYS. Also the validation of methodology is done with comparing the results with that of available in literature and found in well agreement. Further analysis is performed for three sets of power law exponent n = 0, 1 and 100 which gives benchmark results for vibration control of FGM piezoelectric plate.

Keywords:

Functionally Graded Material, Piezoelectric, LQR Controller, Genetic Algorithm

1. Introduction

Functionally graded materials (FGM) take big attention recently; they provide better mechanical behavior in comparison to composite materials, in which they have been emerged in the aerospace, automobile, and nuclear industries. With the increased use of these materials, it’s necessary to get a full understanding of the FGM structures behavior like vibration. The appearance of unwanted vibrations of FGM structures can lead to catastrophic failure. In order to control vibrations, the piezoelectric patches are an effective tool. Huu-Tai Thai and Dong-Ho Choi [1] used a simple first order shears deformation theory for the bending and free vibration analysis of functionally graded plates. Vedat Dogan [2] performed nonlinear vibration of FGM plates under random excitation. Hasani et al. [3] carried out an exact solution for free vibration of thin functionally graded rectangular plates. Preumont [4] studied vibration control of active structures. Fakhari and Ohadi [5] performed nonlinear vibration control of functionally graded plate with piezoelectric layers in which thermal loading is considered. Hossain et al. [6] carried out active vibration control of an FGM rectangular plate using fuzzy logic controllers. Liew et al. [7] studied optimal shape control of functionally graded smart plates using genetic algorithms. Kargarnovin proposed [8] vibration control of a functionally graded material plate patched with piezoelectric actuators and sensors under a constant electric charge. Mao and Fu [9] performed nonlinear dynamic response and active vibration control for piezoelectric functionally graded plate. Ramesh Kumar and Narayanan [10] carried out work on optimal location of piezoelectric actuators and sensors for vibration control of plates. Wankhade and Bajoria [11] [12] studied vibration and buckling analysis of piezolaminated plates using higher order shear deformation theory. Roy and Chakraborty [13] performed optimal vibration control of smart fiber reinforced composite shell structures using improved genetic algorithm. In the present paper a finite element model based on classical plate theory is presented for the vibration control of FGM plate by means piezoelectric layers. The linear quadratic (LQR) control algorithm is used. To improve the LQR controller, the weighting matrices Q and R are chosen based on maximizing the closed loop damping ratio and by using genetic algorithm.

2. Functionally Graded Materials

In literature several computational models have discussed the issue of finding suitable functions for FG material properties, and there are various criteria for selecting them. In the present work the simple power law, which has all the desired properties, is used.

The material proprieties can be expressed as follows:

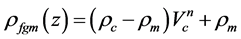
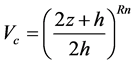(1)

where , , 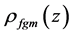and n are Young’s modulus, mass density and the power law exponent. The subscripts m and c represent the metallic and ceramic constituents, respectively; 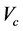is the volume fraction of the ceramic.

Finite Element Modeling

The FGM plate with piezoelectric with integrated piezoelectric sensors and actuators is modeled using the classical plate theory. Two type of rectangular element four-noded and eight noded with three degrees of freedom per node are used. The full derivation and parameters has been presented by K Ramesh Kumar and S Narayanan [10] . The global matrix equations governing a smart structure system can be written as:

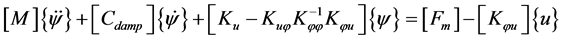(2)

here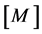, , , 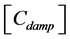and 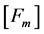are the global mass, stiffness, damping, elastic- electric coupling stiffness matrices and the applied mechanical force.

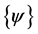denotes structural displacement, and 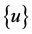denotes electric potential.

The output electrical potential of the sensor is given by

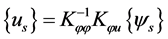(3)

Assuming that the system response is governed by the eigen modes, the displacement can be expressed as

(4)

where are the modal coordinates and is the modal matrix

Introducing the variable the state space equation for the dynamic system Equation (2) can be written as

(5)

where [A] is the system matrix, [B] is the control matrix, which are given by

(6)

where

The output equation can be written as

(7)

present the output matrix which depends on the modal matrix and sensor piezoelectric stiffness matrix.

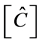
LQR optimal control

The idea beyond the LQR is to minimize a cost function given as

(8)

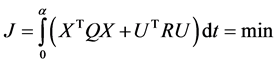
where, the matrices Q and R are weighting matrices. It assumed that the desired state is x = 0, but the initial condition is non-zero, so the matrix Q penalizes the state error in a mean-square sense. Similarly, the matrix R penalizes the control effort, i.e., limits the control signals magnitude. Design the optimal feedback control force U by the application of classical LQR control method:

(9)

The gain matrix which minimizes J can be found by solving a matrix Riccati equation that given by:

(10)

In present work the Q and R matrices are presented as follow:

(11)

Therefore, a search algorithm is required for finding Q and R by taking X₁, X₂, and X₃ as variables to achieve the highest damping effect as follows [11] :

(12)

where is the natural frequency.

3. Results and Discussion

3.1. Model Validation

In order to ensure the accuracy of the proposed finite element model a cantilever FGM plate made of combined aluminum oxide and Ti-6A1-4v materials and bounded by piezoelectric layer on the top and the bottom is considered. Using four and eight node elements of finite element MATLAB code is written to perform a modal analysis to illustrate the eigen frequencies and eigen modes for the FGM plate with integrated piezoelectric layer. The geometry of the considered plate is showed in Figure 1. The thickness of each piezoelectric layer is taken as 0.1 mm. Material properties of plate are presented in Table 1. The initial five frequencies of the plate with piezoelectric layer as a function of the power law exponent “n” for the set boundary conditions are listed in Table 2.

From Table 2 it is observed that proposed finite element methodology can be effectively used for vibration analysis of a cantilever FGM plate composed of aluminum oxide and Ti-6A1-4v materials which is bounded by piezoelectric layer on the top and the bottom of the plate. Both four node and eight node elements of finite element perform well for modal analysis to obtain the eigen frequencies and eigen modes for the FGM plate with integrated piezoelectric layer. The results found are in good agreement with those of and Ansys and He et al. (2001) [14] which demonstrates the efficiency of proposed methodology.

3.2. Vibration Control Analysis

For the vibration control, the top piezoelectric layer is used as an integrated actuator and the bottom layer as an integrated sensor. The LQR control algorithm described earlier is used to control or suppress the vibration of the FGM plate. The genetic algorithm is used to define the weighting parameters based on the Equation (12). Three set of power law exponent n = 0, 1 and 100 are presented. To make a good decision of choosing the best solutions of Q and R parameters the genetic algorithm MATLAB code is set ten times for hundred generations. The weighting parameters using for the optimal [Q] and [R] for each case in this study are present in Table 3. Results for vibration control of FGM plates with a mixture of metal and ceramic are presented in further with genetic algorithm LQR control. Closed loop damping rations are found out for the corresponding set of power law exponent.

Figure 2 shows the GA-LQR controlled non-dimensional deflection histories for n = 0 (full metal). In this case the closed-loop damping ratio is found to be 5.2% moreover the settle time of the vibration is about 0.35 s. The required voltage is also presented in the same figure. For the case of n = 1 the closed-loop damping ratios achieved 6.3% while the time require to return the plate to equilibrium 0.3 s.

From Figure 3 depicted the GA-LQR controlled non-dimensional deflection histories for n = 1 (50% metal and 50% ceramic). In this case the closed-loop damping ratios achieved are 6.3% and the settling time is 0.3 s. The required voltage to damp the plate is also presented.

Figure 4 demonstrate the non-dimensional deflection of the cantilever FGM plate in controlled and uncontrolled response is considered with respect to time. The deflection is shown for n = 100 and the corresponding actuator voltages are also presented.

It is observed from Figure 4 that the GA-LQR significantly controlled non-dimensional deflection histories for the case of n = 100 (full ceramic). In this case the closed-loop damping ratios achieved as 8.9% while the settle time is 0.2 s. The required actuator voltages are given in the same figure.

4. Conclusion

The present work investigates the active vibration control of FGM plate with integrated piezoelectric layers. A FGM plate with piezoelectric actuator and sensor at top and bottom face is considered for the study. Simple power-law distribution in terms of the volume fraction of the constituents is adopted for considering the material properties to be graded along the thickness of the plate. A finite element method based on classical plate theory is used for two cases considering four and eight nodes finite element. The LQR weighting parameters are chosen based on maximizing the closed loop damping ratio via genetic algorithm technique. Various results are presented to show the accuracy and validation of the present method. The control low is presented for different sets of power law exponent n = 0, 1 and 100. The closed loop damping ratios are found to be 5.2%, 6.3% and 8.9% respectively for each case.

Cite this paper

Kouider Bendine,Rajan L. Wankhade, (2016) Vibration Control of FGM Piezoelectric Plate Based on LQR Genetic Search. Open Journal of Civil Engineering,06,1-7. doi: 10.4236/ojce.2016.61001

References