Open Journal of Civil Engineering
Vol.2 No.3(2012), Article ID:22976,9 pages DOI:10.4236/ojce.2012.23014
Improvement of Concrete Shear Wall Structures by Smart Materials
1School of Civil Engineering, University of Tehran, Tehran, Iran
2Civil & Environmental Engineering Department, University of California, Los Angeles, USA
Email: *mghassem@ut.ac.ir
Received May 7, 2012; revised June 10, 2012; accepted June 20, 2012
Keywords: Smart Material; Shape Memory Alloy; Shear Wall; Superelasticity; Seismic Behavior
ABSTRACT
Smart materials have found numerous applications in many areas in civil engineering recently. One class of these materials is shape memory alloy (SMA) which exhibits several unique characteristics such as superelasticity and shape memory effect. Due to these characteristics, research efforts have been extended to use SMA in controlling civil structures. This paper investigates the effectiveness of SMA reinforcements in enhancing the behavior of shear walls, especially when subjected to seismic excitations. Two ordinary and coupled shear walls were introduced as reference structures and were modeled by ABAQUS software. For improving the seismic response of the shear walls, vertical SMA reinforcing bars were proposed to be implemented like conventional steel reinforcements, throughout the height of the structures and in every connecting beam in the coupled shear wall system. The one dimensional superelastic model of SMA material was implemented in the computer software using FORTRAN code. The dynamic response of the shear walls subjected to seismic loading was investigated through time history analyses under El-centro and Koyna records. The results showed that using superelastic SMA material instead of steel bars caused remarkable reduction in residual displacement for both ordinary and coupled shear walls. In addition, SMA reinforcements could significantly decrease the maximum deflection of the coupled shear wall system.
1. Introduction
Many multi-storey buildings contain shear walls around the elevator shafts and stairwells as lateral resisting systems. For the concrete shear wall systems, it is difficult to satisfy the very ductile behavior conditions. Therefore, such structures have often suffered damages caused by earthquake events. Shearing damage, bending damage, sliding and overturning damage are usually four kind of damage occur in concrete shear wall during earthquake. If concrete shear wall can attain their initial shape after an earthquake, then problems associated with permanent damage can be addressed. Sometimes, there are several openings in these shear walls and if two such openings are on opposite sides, deep coupling beams are supposed to interconnect the walls. These coupling beams are generally used as a means of dissipating energy during earthquakes through experiencing inelastic yielding. Due to their small span to depth ratio, they require highly congested reinforcement in order to achieve ductile behavior. Although dissipating energy through plastic hinging is a common practice in the design of multi-storey buildings, this practice usually results in significant residual displacements and the need to repair the structural elements after the earthquake. To address the shortcomings of current practices, a new design approach using smart materials such as shape memory alloy (SMA) is proposed.
SMA is one example of smart materials that exhibit several unique characteristics such as shape memory effect, superelasticity, and energy dissipation features. Due to these characteristics, Shape Memory Alloys have widely attracted attentions in passive control of structures in recent years. Dolce, et al. in a series of publications studied the effectiveness of SMA materials for use in seismic applications [1]. They also studied the implementation of various states of SMA materials for the use of special dampers in structures. They proposed different recentering or dissipating devices based on experimental results. Wilde et al. performed an analytical study of SMA-based seismic isolation system consist of laminated rubber bearing and superelastic SMA bars [2]. They conducted time history analysis with different excitation to compare the SMA-based bearing with conventional bearing with lead core. Dolce and Cardone experimentally investigated the proper choice of alloy, the effect of temperature, SMA size and loading rate and number of cycles [3]. Bruno and Valente showed the effectiveness of the use of SMA materials by analytical measures using simple pseudoelastic constitutive model for SMAs using damage index approach [4]. Baratta and Corbi analyzed the dynamics of a structural elastic-plastic frame, endowed with pseudoelastic SMA tendons [5]. DesRoches and Delemont evaluated the efficiency of using SMA restrainers to reduce the response of decks in a multi span simply supported bridge [6]. Masuda and Noori investigated the optimization of hysteretic characteristics of damping devices based on pseudoelastic SMAs [7]. DesRoches et al. experimentally evaluated the properties of superelastic Ni-Ti shape memory alloys under cyclic loading to assess their potential for applications in seismic resistant design and retrofit [8]. Abolmaali et al. compared the energy dissipative characteristics of bolted t-stub connections using steel and shape memory alloy (SMA) fasteners [9]. Choi et al. proposed a new SMArubber bearing which is composed of a conventional elastomeric bearing and SMA wires wrapping the bearing in longitudinal direction [10]. A multilinear constitutive model developed by Motahari and Ghassemieh was adopted to capture the most common behaviors of SMA [11]. Czaderski et al. tested a reinforced concrete (RC) beam equipped with SMA material and compared it with conventional RC beam [12]. The results proved that by using shape memory alloys it is possible to produce a RC beam which has variable stiffness and strength. Saiidi and Wang presented the application of SMA bars instead of steel bars in plastic hinge zone of reinforced concrete bridge piers [13]. Motahari et al. also introduced a special SMA damper to have both re-centering and energy dissipating characteristics simultaneously [14]. Li et al. experimentally studied the behavior of smart concrete beams with embedded shape memory alloy bundles [15]. They used SMA bundles as actuators to achieve recovery force. Andrawes and DesRoches compared the efficiency of SMA restrainers with three other retrofit devices including conventional steel restrainers, metallic dampers and viscoelastic dampers [16]. Johnson et al. conducted a large scale testing program to evaluate the effect of SMA restrainer cable on the seismic performance of in-span hinges of multiple-frame concrete box girder bridge subjected to strong ground motion [17]. Rahman et al. investigated the effect of cross section geometry on the bending of a beam and also buckling of a column made of SMA through a numerical study [18]. Sharabash and Andrawes studied the application of SMAs as seismic passive damper devices for vibration mitigation of cable stayed bridges [19]. The feasibility of superelasticity in increasing ductility capacity and decreasing residual displacement of concrete bridge column was investigated by Saiidi et al. [20]. Ozbulut and Hurlebaus explored the effectiveness of SMA-rubber based isolation systems for seismic protection of bridges against near-field earthquakes. They also compare the performance of SMArubber based isolation systems with SMA-based sliding isolation system [21]. Kari et al. evaluated the effectiveness of a new dual bracing system for improving the seismic behavior of steel structures [22].
In this study the behavior of concrete shear walls reinforced with SMA bars is investigated. Finite element program, ABAQUS, was used in order to assess the response of the structures subjected to seismic loading. Two ordinary and coupled shear walls were introduced as reference structures and their seismic behavior with and without SMA reinforcement was evaluated through time history analyses.
2. Shape Memory Alloy
Shape Memory Alloys are new class of metallic alloys that display multiple incomparable characteristics, based on martensitic phase transformation. SMAs are able to undergo large strains (8% - 10%) without leaving permanent deformations in the material. They can recover their initial shape at the end of the deformation process, instinctively (called superelasticity) or by heating (called shape memory effect) as shown in Figure 1. The most
 (a) (b)
(a) (b)
Figure 1. Stress-strain curves for SMAs: (a) superelasticity effect; (b) shape memory effect.
favorable characteristic of SMAs which is used in passive control of structures is superelastic behavior in which the material can recover large deformations of order of 8 percent while producing flag-shaped hysteresis. The second feature of the SMA is the shape memory effect. When the material is in Martensite form, application of stress leads to twinning of Martensite. By removal of stress the detwinning process begins and at the zero stress, some residual strain will be remained that can be recovered by heating the material above a specific temperature. Other desirable characteristics of SMAs are high energy dissipation capacity, stability of hysteresis loop and high fatigue resistance. Added to all those characteristics, the relatively high stiffness and strength makes SMA a promising material for control of structures in severe earthquakes. Although several alloys have the shape memory feature, the most widely used SMA in civil engineering applications is Nitinol, which is a combination of Nickel and Titanium. However, since Nitinol is a very expensive material compared to steel, it may not be economical to use it unless high energy dissipation is demanded.
3. Analytical Models of Shear Walls
This study investigates the seismic performance of two concrete shear wall structures equipped with superelastic SMA. The first structure had the width of 5.0 m, height of 15.0 m and thickness of 0.3 m. The second structure was a coupled shear wall with two interconnected concrete walls. Each wall had the width of 3.0 m, height of 15.0 m and thickness of 0.3 m and each coupling beam was 0.6 m deep, 2.4 m length with 0.3 m width. Height between each level was fixed at 3.0 m. In order to attain the numerical behavior of the structures, finite element computer program (ABAQUS) was used in this study [23]. Finite Element models of the first and the second shear walls are presented in Figures 2 and 3, respectively. Concrete material had compressive strength of 32 MPa, Young’s modulus of 30 GPa, poisson ratio of 0.2, and density of 25 kN/m3. Concrete damage plasticity, developed by Lee and Fenves [24] was utilized for a proper material modeling of the concrete behavior in the numerical analyses. Lumped masses were placed at each node at story levels to represent the lateral inertial loads induced from the floor to the walls in time of earthquake excitations.
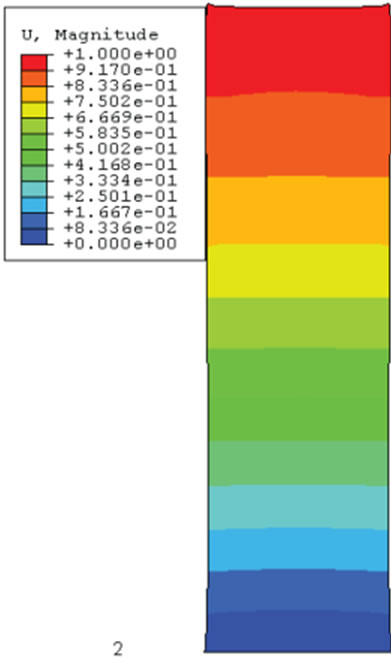
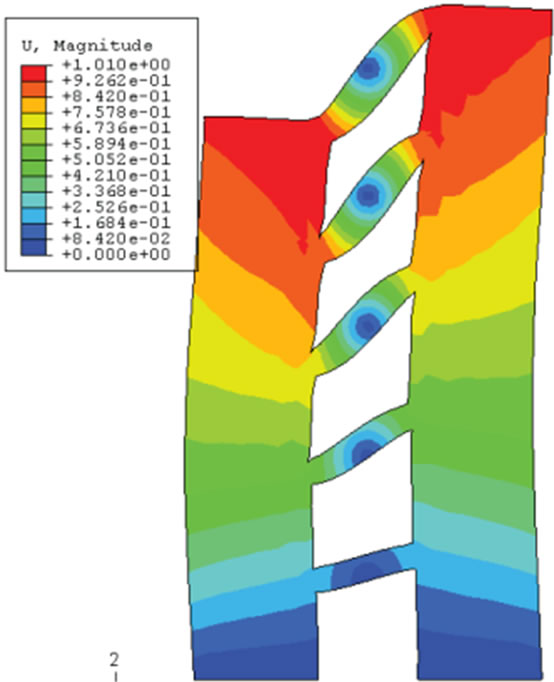
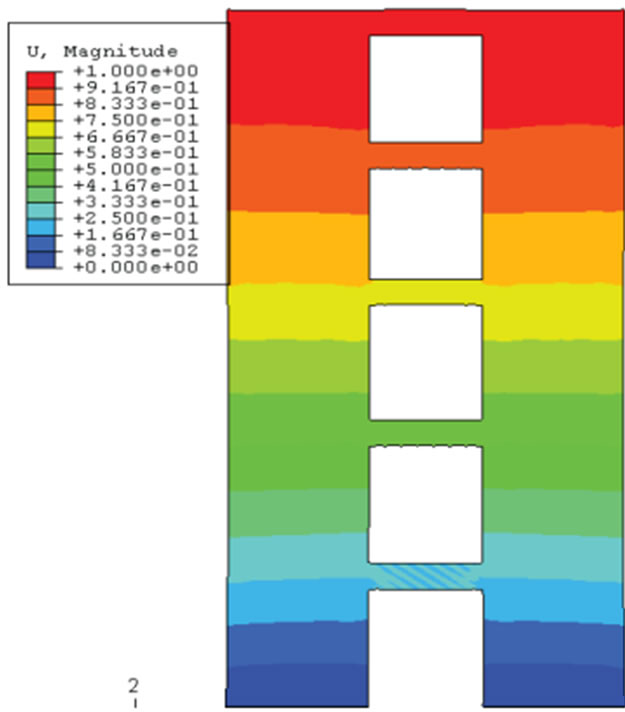
In order to grant better understanding of the dynamic behavior of the shear walls, a modal analysis was conducted for the reference structures by the ABAQUS computer program. Mode shapes and natural period of each mode are presented in Figures 4 and 5. As illustrated, the first three fundamental periods of the first shear wall were 0.726, 0.157 and 0.134 sec, respectively and the coupled shear wall had the first three periods of 0.828, 0.202 and 0.131 sec, respectively.
4. Proposed Enhancement Technique
The proposed method uses SMAs as reinforcement in the concrete shear wall for the purposes of eliminating the residual displacement. For the upgraded structure, vertical SMA reinforcing rebars were proposed to be implemented like conventional steel reinforcements, throughout the height of the wall structures and in the all five connecting beams in coupled shear wall. No diagonal rebars were used as reinforcements in this research. For reaching the different percentages of reinforcements, the SMA and steel rebars were studied to posses various diameters and spacing. Since in the ABAQUS finite element program, the SMA mechanical behavior does not appear by default, thus the SMA material was implemented in the computer program by writing a subroutine using FORTRAN and attaching it to the main program as a subroutine material module.

Figure 2. Finite element model of the ordinary shear wall without openings.
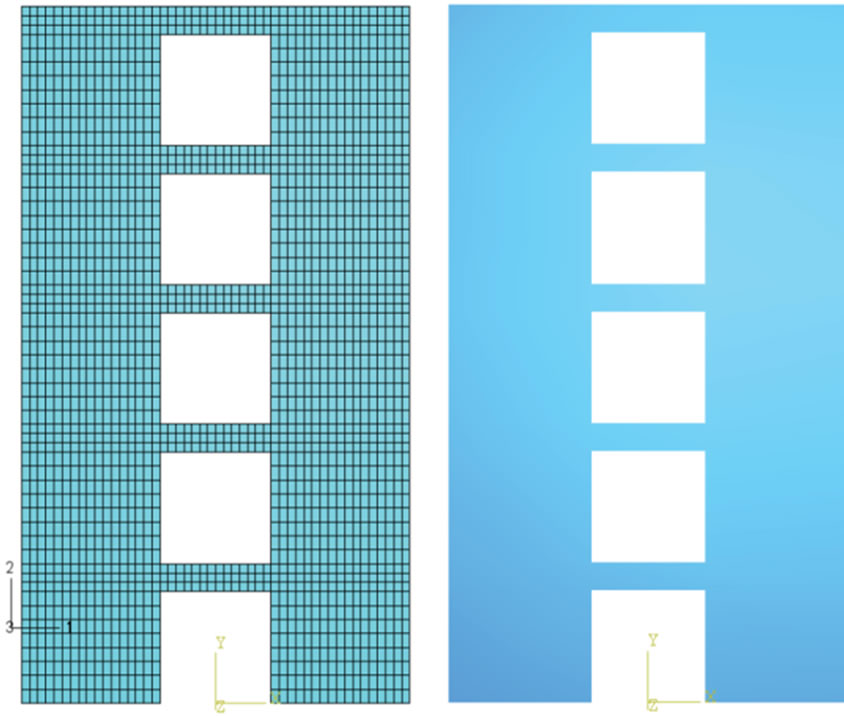
Figure 3. Finite element model of the coupled shear wall.

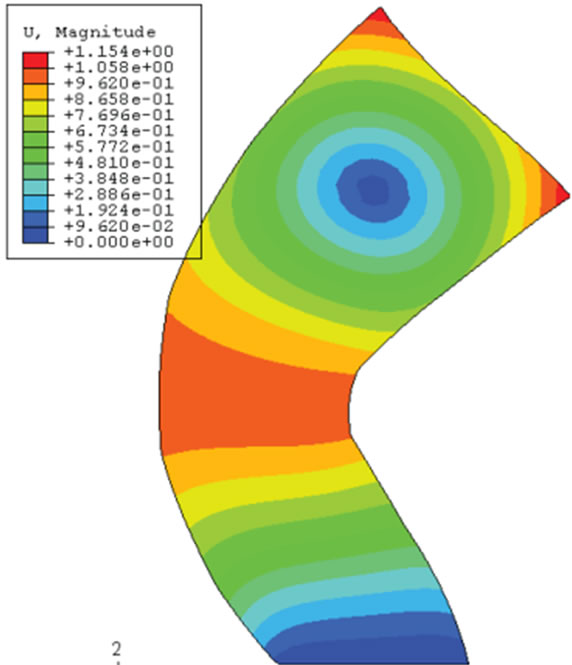

(a) 1st mode shape (Tn1 = 0.726) (b) 2nd mode shape (Tn2 = 0.157) (c) 3rd mode shape (Tn3 = 0.073)
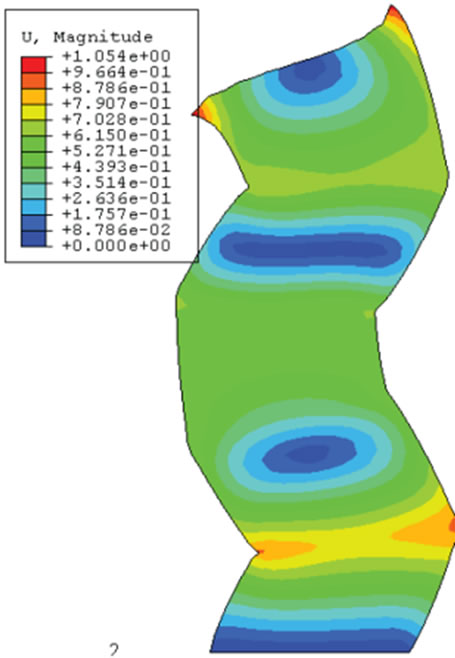
(d) 4th mode shape (Tn4 = 0.134) (e) 5th mode shape (Tn5 = 0.050)
Figure 4. Mode shapes of the first shear wall.

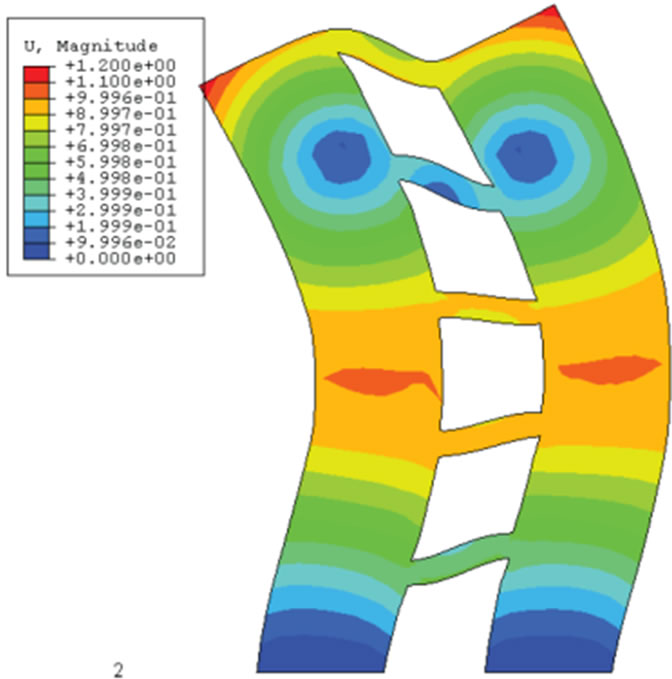
(a) 1st mode shape (Tn1 = 0.828) (b) 2nd mode shape (Tn2 = 0.202) (c) 3rd mode shape (Tn3 = 0.131)

(d) 4th mode shape (Tn4 = 0.144) (e) 5th mode shape (Tn5 = 0.091)
Figure 5. Mode shapes of the second coupled shear wall.
Since most civil engineering applications of SMA are related to the use of bars and wires, one dimensional phenomenological models are often considered suitable. Several researchers have proposed uniaxial models for SMA. Figure 6 shows the 1D-superelastic model of SMA material [11] implemented in the computer model. This model is capable of describing the constitutive behavior of superelastic SMAs at a constant temperature. The model requires 6 material parameters. The parameters used to define the material model are austenite to martensite starting stress (σam-s), austenite to martensite finishing stress (σam-f), martensite to austenite starting stress (σma-s), martensite to austenite finishing stress (σma-f), superelastic plateau strain length (εL), and modulus of elasticity (EA). The SMA model represents an idealized behavior for SMA material where no strength degradation occurs during cycling and the residual deformation is taken zero at the end of each cycle. Further assumption is that austenite and martensite branches have the same modulus of elasticity (β = 1). Previous studies have shown that such simplifications generally have negligible effect on the response [25]. Table 1 shows SMA mechanical properties defined in ABAQUS computer program as “User Implemented Material”.
5. Analyses and Results
In this section, analyses were undertaken on two shear wall structures to evaluate the effectiveness of the SMA rebars in seismic performance of the concrete walls. The behavior of the structures subjected to earthquake excitations was investigated through dynamic time history analyses on the numerical models, and the response of the structure was attained by subjecting them to the El-centro and Koyna earthquake records. To show the significance of the SMA reinforcements in improving the seismic response, the story displacements at each floor level were obtained from time history analyses. The result of the new proposed system subjected to seismic excitations was then compared with those of the original concrete structure (without SMAs) and also assessed against models with different percentages of SMA reinforcements.

Figure 6. Stress-strain relationship of the superelastic SMA material.
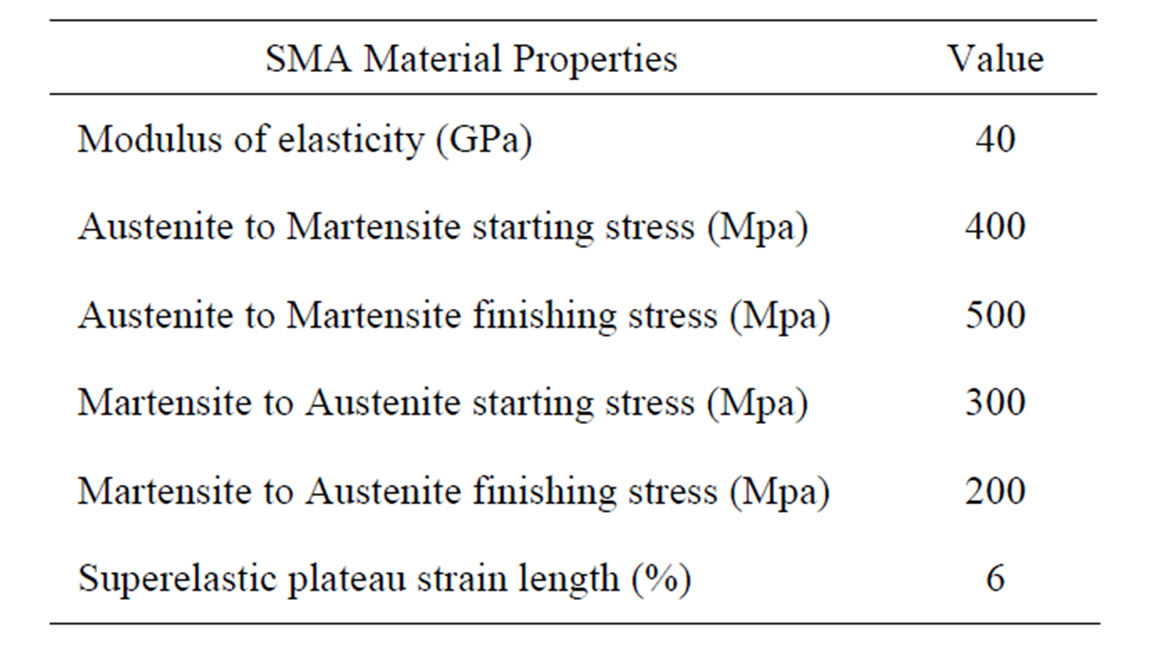
Table 1. SMA mechanical properties.
5.1. The First Shear Wall
Figures 7 and 8 compare the seismic response of the structure with steel or SMA reinforcement subjected to El-centro and Koyna records. The results showed that using superelastic SMA material instead of steel in concrete shear wall can significantly reduce the residual displacement. In particular, in the case of steel reinforcement, the concrete shear wall had residual displacements of 0.05 m and 0.08 m for El-centro and Koyna earthquakes, respectively. In the case of SMA reinforcement, the structure just experienced the residual displacements of 0.02 m and 0.02 m for El-centro and Koyna earthquakes, respectively. These results illustrated 60% and
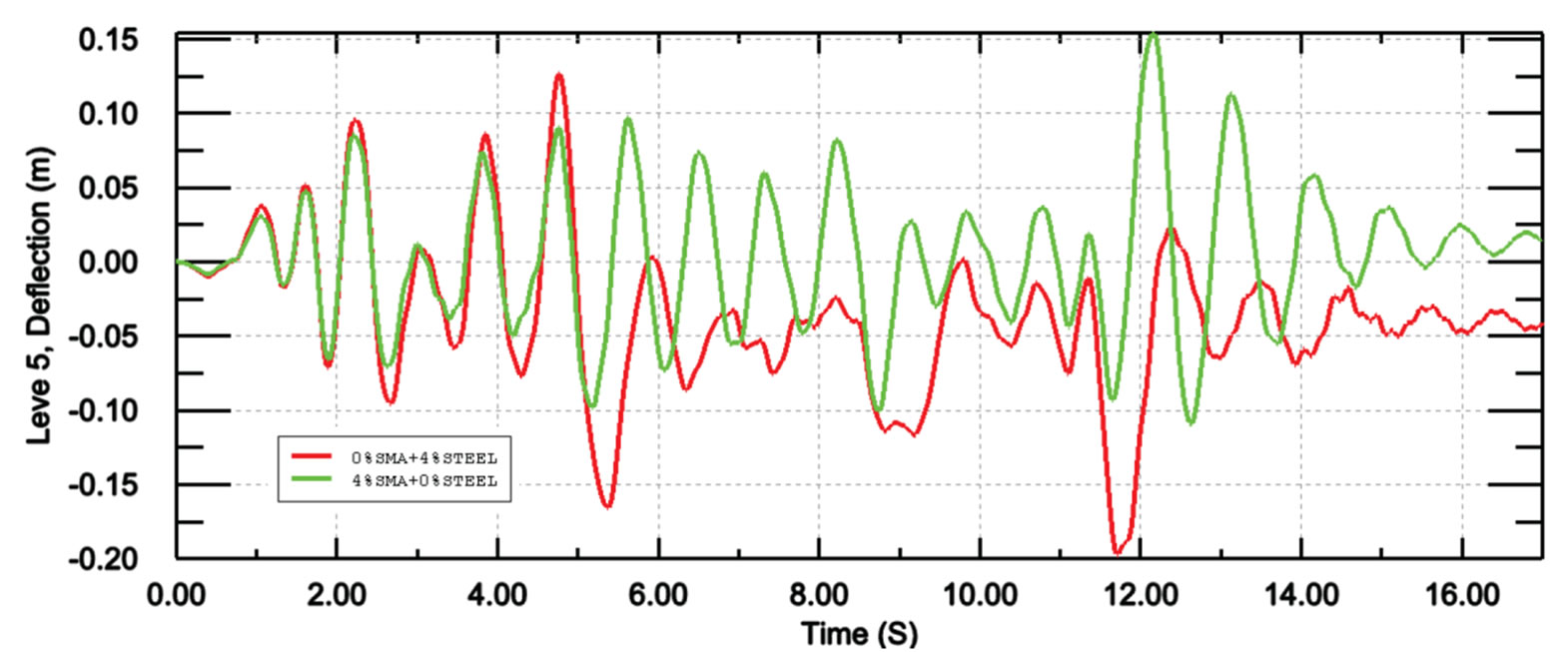
Figure 7. Tip deflection of the shear wall subjected to El-centro earthquake for different types of reinforcement.
75% reduction in the residual displacement of the shear wall for El-centro and Koyna records, respectively. However, the results also showed that SMA reinforcements could not reduce the maximum deflection of ordinary shear walls meaningfully.
The residual deformation of the shear wall subjected to El-centro earthquake for five stories is presented in Figure 9. As illustrated, the SMA reinforcement could successfully reduce the residual displacements compared to steel reinforcement for all five levels. This was mostly due to the superoelasticity feature of the SMA. In other words, in each cycle, shape memory alloys could restore most of the displacement and hence avoided the accumulation of residual displacement in the repeated cycles. Therefore, SMA limited the residual deformation at the end of the record. However, in the case of traditional steel reinforcement, yielding of material might accumulate plastic deformations in loading cycles and hence considerable residual deformation remained in the end of the earthquake.
Figure 10 displays the time histories of tip deflection for 4% and 6% SMA reinforcements in combination with 2% steel reinforcement. It can be observed that adding more SMA reinforcement to steel rebars could reduce both maximum and residual displacements. Specifically, by changing SMA reinforcement from 4% to 6%, the maximum tip displacement of the structure was decreased from 135 mm to 88 mm (46% reduction) and residual displacement was reduced from 30 mm to 15 mm (50% reduction).
5.2. The Second Coupled Shear Wall
Figure 11 compares the seismic response of the coupled shear wall with steel or SMA reinforcement under Koyna earthquake. The result showed that the coupled shear wall with SMA reinforcement experienced much lower level of deflection than the shear wall with steel reinforcement. In particular, in the case of steel reinforcement, the concrete wall had maximum deflection of 0.13 m, while in the case of SMA reinforcement, the structure just experienced the displacement of 0.07 m (i.e. 46% reduction in the maximum displacement). In addition, superelastic SMA reinforcement could significantly reduce the residual displacement of the concrete wall. Specifically, the residual displacement of the structure was reduced from 0.06 m in the original wall to 0.01 m in the controlled structure (i.e. 83% reduction in the residual displacement).
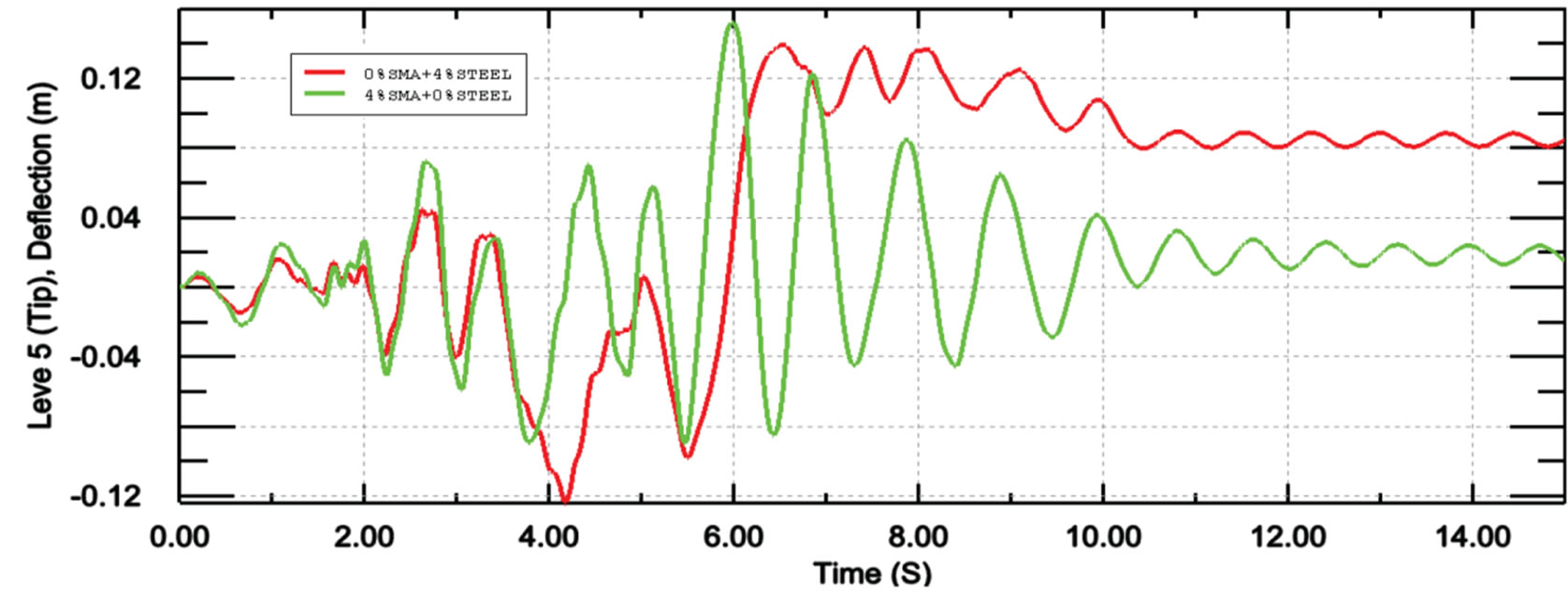
Figure 8. Tip deflection of the shear wall subjected to Koyna earthquake for different types of reinforcement.

Figure 9. Residual deformation of the shear wall subjected to El-centro earthquake in five stories for steel or SMA reinforcements.
The maximum displacement of the coupled shear wall subjected to Koyna earthquake for five levels is illustrated in Figure 12. As it can be observed, using SMA reinforcement could meaningfully reduce the maximum displacement compared to steel reinforcement for all five stories especially for upper levels. This might be due to the fact that SMA bars were superelastic and had the ability to maintain their effective stiffness for repeated cycles while steel bars lost their effectiveness remarkably due to early yielding and caused large displacement in the response history.
Figure 13 displays the time histories of tip deflection for 0% steel and 4% SMA reinforcement and 1.5% steel and 2.5% SMA reinforcement. It can be observed that replacing 1.5% of shape memory alloy rebars by steel rebars did not affect the seismic response significantly and two concrete walls behave similarly under El-centro earthquake. However, since SMA is a very expensive material compared to steel, it may be economical to use it when the steel and SMA reinforcements are well proportioned.
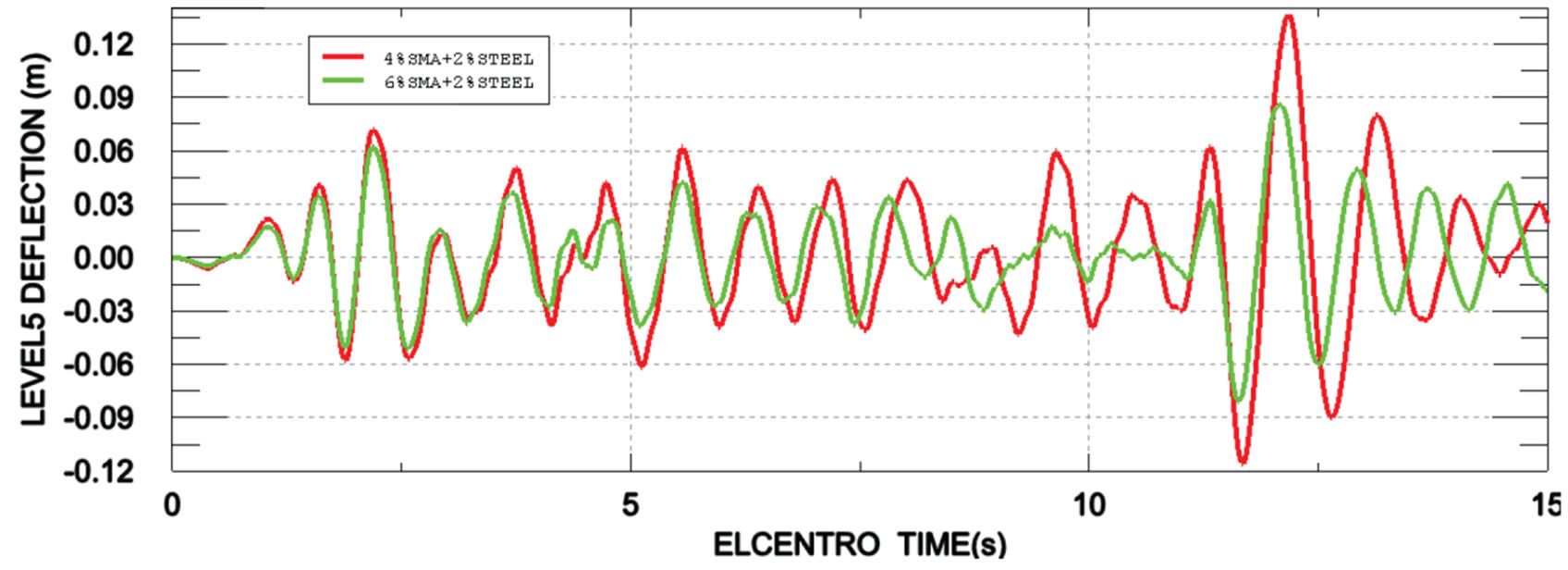
Figure 10. Tip deflection of the shear wall subjected to El-centro earthquake for different combination of SMA with steel reinforcement.
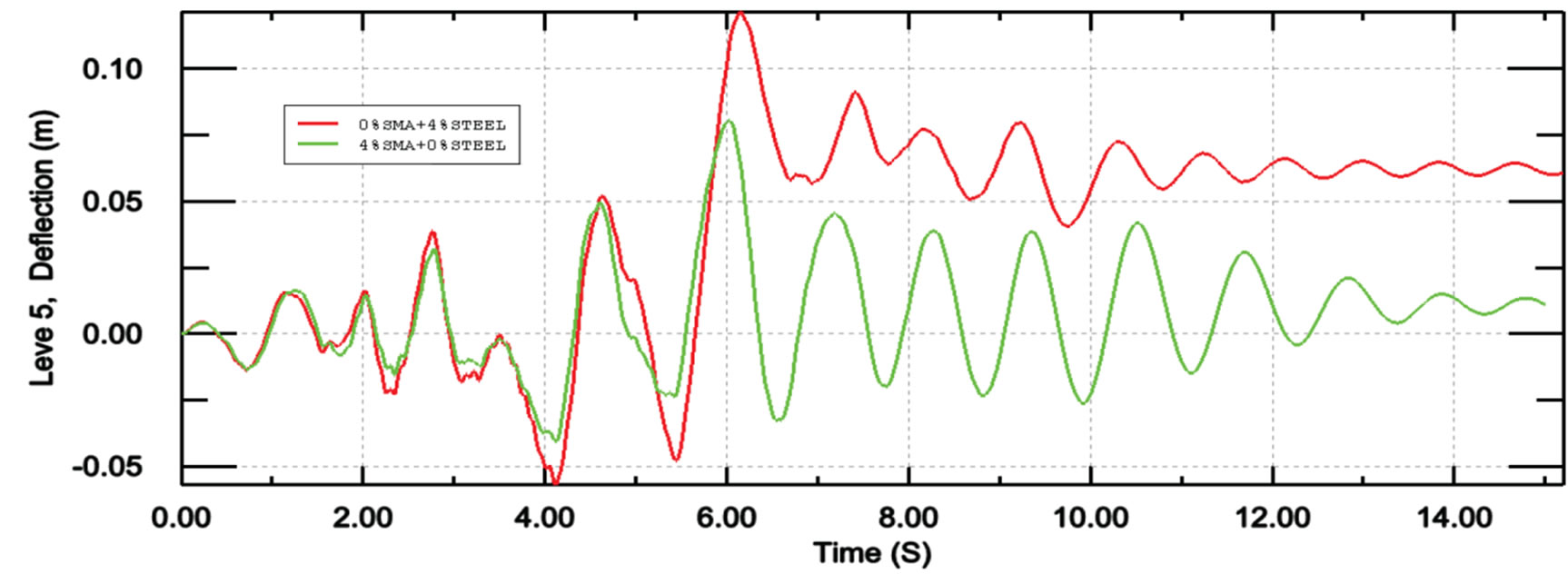
Figure 11. Tip deflection of the coupled shear wall subjected to Koyna earthquake for different types of reinforcement.

Figure 12. Maximum displacement of the coupled shear wall subjected to Koyna earthquake in five stories for steel or SMA reinforcements.
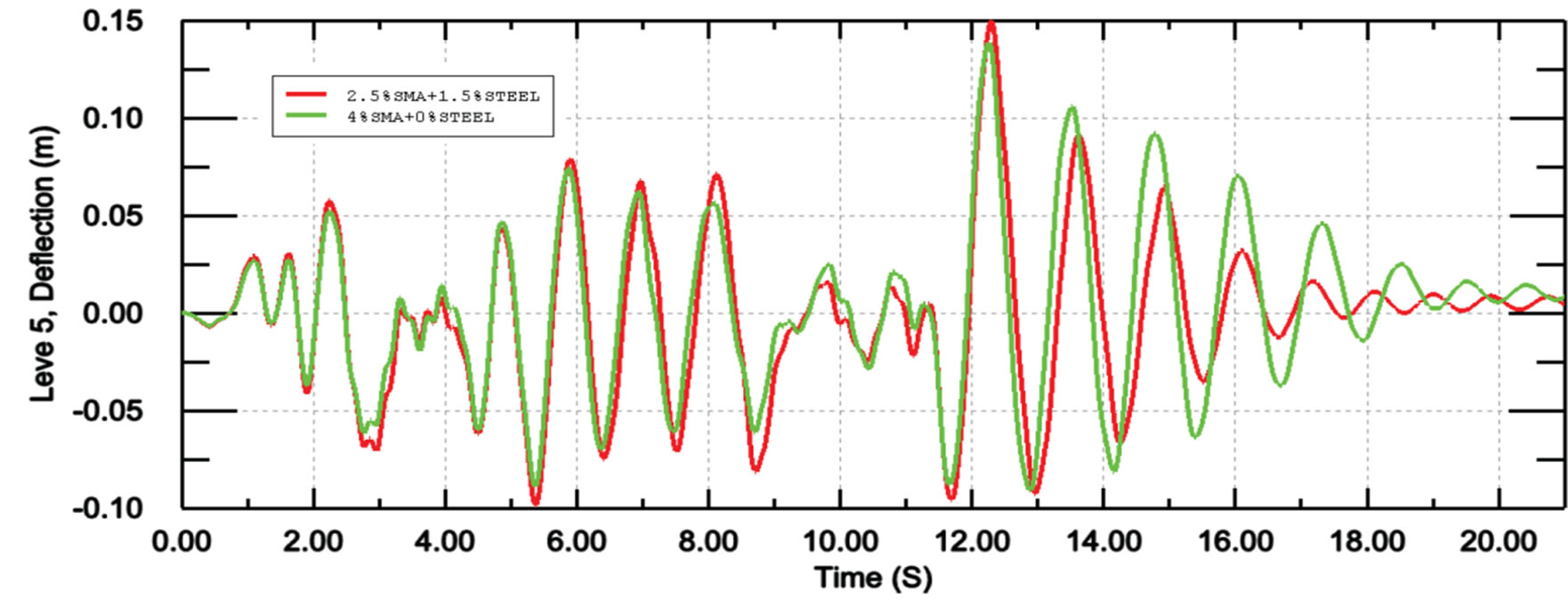
Figure 13. Tip deflection of the shear wall subjected to El-centro earthquake for different reinforcement combinations.
6. Conclusions
In this paper, an analytical study was conducted to evaluate the effectiveness of, one the latest smart material namely, shape memory alloy (SMA) in seismic improvement of concrete shear walls. Two types of shear walls such as ordinary type and coupled shear walls were introduced as reference structures and were modeled by ABAQUS computer program. Modal analyses were performed to capture the modal periods and mode shapes of the shear walls. For improving the seismic behavior of the shear walls, vertical SMA reinforcing bars were proposed to be implemented similar to conventional steel reinforcements, throughout the height of the structures and in all five connecting beams in coupled shear wall. The 1D-superelastic model of SMA material was implemented in the computer program by using FORTRAN as a subroutine material module. The dynamic response of the structures subjected to earthquake excitations was investigated through time history analyses subjected to El-centro and Koyna records.
In the case of the ordinary shear wall, as illustrated, using superelastic SMA material instead of steel rebars caused remarkable reduction in residual displacement. The results showed that SMA bars decreased the residual displacement by 60% and 75% for El-centro and Koyna records, respectively. However, the SMA reinforcements could not reduce the maximum deflection of the shear wall significantly. For the second coupled shear wall, it was observed that the structure with SMA reinforcement experienced lower level of maximum and residual displacements than the coupled shear wall with steel reinforcement. The results indicated that the SMA bars reduced the maximum and residual displacements up to 46% and 83%, respectively compared to the responses of the reference wall under Koyna earthquake.
In addition, different combinations of SMA reinforcement with steel reinforcement were modeled in both reference structures. The results showed that using such combinations of different reinforcement types improved the shear walls performance with an extent that depended on the percentage of SMA reinforcement. However, due to economical consideration, the steel and SMA reinforcements must be proportioned properly.
REFERENCES
- M. Dolce, D. Cardone and R. Marnetto, “Implementation and Testing of Passive Control Devices Based on Shape Memory Alloys,” Earthquake Engineering and Structural Dynamics, Vol. 29, No. 7, 2000, pp. 945-968. doi:10.1002/1096-9845(200007)29:7<945::AID-EQE958>3.0.CO;2-#
- K. Wilde, P. Gardoni and Y. Fujino, “Base Isolation System with Shape Memory Alloy Device for Elevated Highway Bridges,” Engineering Structures, Vol. 22, 2000, pp. 222-229. doi:10.1016/S0141-0296(98)00097-2
- M. Dolce and D. Cardone, “Mechanical Behavior of Shape Memory Alloys for Seismic Applications-2. Austenite NiTi Wires Subjected to Tension,” International Journal of Mechanical Sciences, Vol. 43, No. 11, 2001, pp. 2657- 2677. doi:10.1016/S0020-7403(01)00050-9
- S. Bruno and C. Valente, “Comparative Response Analysis of Conventional and Innovative Seismic Protection Strategies,” Earthquake Engineering and Structural Dynamics, Vol. 31, No. 5, 2002, pp. 11067-11092. doi:10.1002/eqe.138
- A. Baratta and O. Corbi, “On the Dynamic Behavior of Elastic-Plastic Structures Equipped with Pseudoelastic SMA Reinforcements,” Computational Materials Science, Vol. 25, No. 2, 2002, pp. 1-13. doi:10.1016/S0927-0256(02)00245-8
- R. DesRoches and M. Delemont, “Seismic Retrofit of Simply Supported Bridges Using Shape Memory Alloy,” Engineering Structures, Vol. 24, No. 3, 2002, pp. 325- 332. doi:10.1016/S0141-0296(01)00098-0
- A. Masuda and M. Noori, “Optimization of Hysteretic Characteristics of Damping Devices Based on Pseudoelastic Shape Memory Alloys,” International Journal of Non-Linear Mechanics, Vol. 37, No. 8, 2002, pp. 1375- 1386. doi:10.1016/S0020-7462(02)00024-0
- R. DesRoches, M. Delemont and J. McCormick, “Cyclical Properties of Superelastic Shape Memory Alloys,” ASCE Journal of Structural Engineering, Vol. 130, No. 1, 2004, pp. 38-46. doi:10.1061/(ASCE)0733-9445(2004)130:1(38)
- A. Abolmaali, J. Treadway, P. Aswath, F. K. Lu and E. McCarthy, “Hysteresis Behavior of T-Stub with Superelastic Shape Memory Fasteners,” Journal of Constructional Steel Research, Vol. 62, No. 8, 2006, pp. 831-838. doi:10.1016/j.jcsr.2005.11.017
- E. Choi, T.H. Nam, J.T. Oh and B.S. Cho, “An Isolation Bearing for Highway Bridges Using Shape Memory Alloys,” Material Science and Engineering A, Vol. 438-440, 2006, pp. 1081-1084. doi:10.1016/j.msea.2006.05.098
- S. A. Motahari and M. Ghassemieh, “Multilinear Onedimensional Shape Memory Material Model for Use in Structural Engineering Applications,” Engineering Structures, Vol. 29, No. 6, 2006, pp. 904-913. doi:10.1016/j.engstruct.2006.06.007
- C. Czaderski, B. Hahnebach and M. Motavalli, “RC Beam with Variable Stiffness and Strength,” Construction and Building Materials, Vol. 20, No. 9, 2006, pp. 824- 833. doi:10.1016/j.conbuildmat.2005.01.038
- S. Saiidi and H. Wang, “Exploratory Study of Seismic Response of Concrete Columns with Shape Memory Alloys Reinforcement,” ACI Structural Journal, Vol. 103, No. 3, 2006, pp. 436-443.
- S. A. Motahari, M. Ghassemieh and S. A. Abolmaali, “Implementation of Shape memory Alloy Dampers for Passive Control of Structures Subjected to Seismic Excitations,” Journal of Constructional Steel Research, Vol. 63, No. 12, 2007, 1570-1579. doi:10.1016/j.jcsr.2007.02.001
- L. Li, Q. Li and F. Zhang “Behavior of Smart Concrete Beams with Embedded Shape Memory Alloy Bundles,” Journal of Intelligent Material Systems and Structures, Vol. 18, No. 10, 2007, pp. 1003-1014. doi:10.1177/1045389X06071974
- B. Andrawes and R. DesRoches, “Comparison between Shape Memory Alloy Seismic Restrainers and Other Bridge Retrofit Devices,” Journal of Bridge Engineering, Vol. 12, No. 6, 2007, pp. 700-709. doi:10.1061/(ASCE)1084-0702(2007)12:6(700)
- R. Johnson, J. E. Padgett, M. E. Maragakis, R. DesRoches and M. S. Saiidi, “Large Scale Testing of Nitinol Shape Memory Alloy Devices for Retrofitting of Bridges,” Smart Material and Structures, Vol. 17, No. 3, 2008, pp. 1-28. doi:10.1088/0964-1726/17/3/035018
- M. A. Rahman, S. R. Akanda and M. A. Hossain, “Effect of Cross Section Geometry on the Response of an SMA Column,” Journal of Intelligent Material Systems and Structures, Vol. 19, No. 2, 2008, pp. 243-252.
- A. M. Sharabash and B. Andrawes, “Application of Shape Memory Alloy Dampers in the Seismic Control of Cable-Stayed Bridges,” Engineering Structures, Vol. 31, No. 2, 2009, pp. 607-616. doi:10.1016/j.engstruct.2008.11.007
- S. Saiidi, M. O’Brien and M. Sadrossadat-Zade, “Cyclic Response of Concrete Bridge Columns Using Superelastic Nitinol and Bendable Concrete,” ACI Structural Journal, Vol. 106, No. 1, 2009, pp. 69-77.
- O. E. Ozbulut and S. Hurlebaus, “Seismic Assessment of Bridge Structures Isolated by a Shape Memory Alloy/ Rubber-Based Isolation System,” Smart Materials and Structures, Vol. 20, No. 1, 2011, pp. 1-15. doi:10.1088/0964-1726/20/1/015003
- A. kari, M. Ghassemieh and A. Abolmaali, “A New Dual Bracing System for Improving the Seismic Behavior of Steel Structures,” Smart Materials and Structures, Vol. 20, No. 12, 2011, pp. 1-35. doi:10.1088/0964-1726/20/12/125020
- Abaqus, Inc., ABAQUS User Manual, V6.4, 2006.
- J. Lee and G. L. Fenves, “A Plastic-Damage Model for Cyclic Loading of Concrete Structures,” ASCE Journal of Engineering Mechanics, Vol. 124, No. 8, 1998, pp. 892- 900. doi:10.1061/(ASCE)0733-9399(1998)124:8(892)
- B. Andrawes and R. DesRoches, “Sensitivity of Seismic Applications to Different Shape Memory Alloy Models,” Journal of Engineering Mechanics, Vol. 134, No. 2, 2008, pp. 173-183. doi:10.1061/(ASCE)0733-9399(2008)134:2(173)
NOTES
*Corresponding author.

