Modern Mechanical Engineering
Vol.05 No.03(2015), Article ID:57846,19 pages
10.4236/mme.2015.53005
Whirl Interaction of a Drill Bit with the Bore-Hole Bottom
Nabil W. Musa1*, V. I. Gulyayev2, L. V. Shevchuk2, Hasan Aldabas1
1Department of Mechanical Engineering, Philadelphia University, Amman, Jordan
2Department of Mathematics, National Transport University, Kyiv, Ukraine
Email: *nmusa@philadelphia.edu.jo, valery@gulyayev.com.ua, Ludmilashevchuk25@gmail.com, haldabbas@philadelphia.edu.jo
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 May 2015; accepted 7 July 2015; published 10 July 2015
ABSTRACT
This paper deals with the theoretic simulation of a drill bit whirling under conditions of its contact interaction with the bore-hole bottom rock plane. The bit is considered to be an absolutely rigid ellipsoidal body with uneven surface. It is attached to the lower end of a rotating elastic drill string. In the perturbed state, the bit can roll without sliding on the bore-hole bottom, performing whirling vibrations (the model of dynamic equilibrium with pure rolling when maximum cohesive force does not exceed the ultimate Coulombic friction). To describe these motions, a nonholonomic dynamic model is proposed, constitutive partial differential equations are deduced. With their use, the whirling vibrations of oblong and oblate ellipsoidal bits are analyzed, the functions of cohesive (frictional) forces are calculated. It is shown that the system of elastic drill string and ellipsoidal bit can acquire stable or unstable whirl modes with approaching critical Eulerian values by the parameters of axial force, torque and angular velocity. The analogy of the found modes of motions with ones of the Celtic stones is established. It is shown that the ellipsoidal bits can stop their whirling vibrations and change directions of their circumferential motions in the same manner as the ellipsoidal Celtic stones do. As this takes place, the trajectories of the oblate ellipsoidal bits are characterized by more complicated paths and irregularities.
Keywords:
Deep Drilling, Ellipsoidal Bits, Nonholonomic Dynamics, Celtic Stones, Instability, Forward and Backward Whirling Motions

1. Introduction
Late in the 19th century, one of the most fascinating dynamic effects of the nonholonomic mechanics was found. It is associated with the so called problem of Celtic stones consisting in the apparent violation of the physical law of angular momentum conservation. This phenomenon is realized for solid ellipsoidal bodies with some breakdowns of geometry or inertia symmetries (the Celtic stones). If to put this body into touch with an uneven horizontal plane and to twirl it around the vertical axis, then, after a time, it ceases to rotate and after some short-run irregular vibration relative to a horizontal axis (“dances”), it again begins to rotate around the vertical axis, yet this time, in the opposite direction.
The similar changes of the rotation directions occur repeatedly for some shapes of bodies. In so doing, the point of the body contact with plane traces out a rather complicated paths. At the stages of rotary motions, they have the shapes of expanding or narrowing spirals, while during the transition through the vibration regimes they acquire the outlines of complicated curves with loops and cuspidal points.
The curious stones possessing these properties were originally called celts because their behavior was discovered by archaeologists studying the prehistoric utensils of ancient Celtic folks. The first description and physical explanation of their motion was presented by G.T. Walker in 1895 [1] . Subsequently, two basic dynamic models were used for analysis of queer behavior of the Celtic stones. The more general and complex statement of the problem consists in investigation of the body motion on the horizontal plane with allowance made for the sliding effect and presence of a friction force at the contact point between the bodies. By virtue of its severity, it turned out to be less attractive and fruitful. The nonholonomic model of the Celtic stone motion was found to be simpler and more obvious, so with its aid, the principal properties and qualitative features of the body motion were revealed [2] - [4] .
The outwardly similar motions can be performed by the polycrystalline-diamond-compact (PDC) bit of a deep drill string (DS). As the bit is connected to the lower end of the DS, their motions are interdependent. In drilling, the DS thrusts the bit against the bore-hole bottom and by-turn is subjected to action of the vertical reaction force, torque and centrifugal inertia force, which conduce to decrease its bending stiffness and lead to its elastic bending. As noted in [5] - [7] , in consequence of its deforming, the coaxiality of the DS and bit is disaligned, the bit shifts out of the system center and begins to roll on the bore-hole bottom.
In this case, two motion regimes are possible which are differed by the character of the bit interaction with the bore-hole bottom and, consequently, are described by different mathematic models. Thus, if the force of the bit thrust to the bottom is not large and adhesion between them is disrupted, then the typical frictional interaction described by the Coulomb friction law prevails. Analysis of the bit dynamics is performed with the use of such model in paper [8] .
But the situation changes essentially with enlargement of the compressive thrust force and its approaching to the Eulerian critical value. Then, the bending stiffness of the DS reduces, it hogs and the diamond impregnations existing in the bit surface penetrate into the rock medium. As this takes place, the bit axis tilts and nutates. It should be particularly emphasized that at this stage, the bit is under action of the vertical force (weight on bit) which essentially exceeds all other forces. It presses the bit to the hole bottom (not to the hole wall) and the bit loses its ability to slide on the bore-hole bottom and begins to roll on its surface, lagging behind or outstripping the DS rotation. As a result, the point of the bit contact with the reference surface (the instantaneous centre of velocities) may describe extremely complicated trajectories with loops and cuspidal points and to change the motion directions, as happens with the Celtic stones.
Analyses of such systems motions were performed, for the most part, with the use of natural models or with the help of simplified mathematic models. In early study of 1990, Brett et al. [9] assumed with the use of simple mass-spring model that the main cause of PDC bit failures was their backward whirl, representing a specific kind of its lateral vibration. That is, a bit may vibrate laterally but may not necessarily be whirling. Only when the bit’s geometric center moves around the hole’s center line is the bit valid whirling. During whirl, the instantaneous center of rotation moves around the bit, and it whirls backward around the hole. Cutters on a whirling bit can move sideways, backward, and much faster than those on a true rotating bit. Laboratory and field results showed the detrimental effects of whirl on the bit rate of penetration and its life. Special attention was also paid to mechanisms of cutting and moving of bits with sharp and dull cutters. In 1992 Langeveld [10] elaborated fully dynamic and three-dimesional model of torsional, axial and lateral vibrations of different PDC bit designs. His analyses demonstrated that conventional PDC bits tend to whirl backward, while anti-whirl PDC bits effectively reduce this tendency and whirl forward. The possibility to vibrate with backward and forward whirlings was noted also by Schen et al. [11] and Thor Viggo and Age [12] . In their observations, the whirl rotation occurred several times per revolution of the bit and during whirl, the bit drilled an overgage hole with a multilobed cross-section. Chen et al. [13] accentuated that in most cases bit whirl (backward or forward) is coupled with other forms of lateral vibrations, therefore, the trajectory of the bit center is usually not a circle. Wu et al. [14] and Ledgerwood et al. [15] [16] bind initiation of whirling vibrations with torsional stick/slip friction vibrations and consider it to be the primary cause of bit damage. Sowers et al. [17] maintain this point of view and assert that additional detrimental effects caused by coupling of these phenomena include the development of ledges, bore-hole oscillations and spiraling, and premature failure of downhole tools. They consider that bore-hole quality can be improved via the use of roller reamers. Johnson [18] points out that bit whirl is responsible for bit-rock interaction, leading to lateral vibrations, and results in short runs, low rate of penetration, high cost per foot, poor hole quality, and downhole-tool damage. The methods developed for the bit whirl reduction is recorded to mitigate the detrimental effects, but do not completely eliminate them and there are compromises associated with each method that prevent their usage in many applications. Friction force influence on the bit whirling is discussed by Christoforou and Yigit [6] and Leine et al. [7] . With the use of low degree of freedom models, simulating the bit rolling on the well wall surface, they provide qualitative insight into rolling with sliding and pure rolling. As shown by calculations, for the time duration covered by simulation, the initial forward whirl changes into a transitory phase, in which the whirl direction continuously changes between forward and backward, and eventually settles into a backward whirl. Note once more, that the similar motions are performed by Celtic stones [1] - [4] . The difference between sliding and rolling motions is also emphasized by Stroud et al. [19] : “Backward whirl occurs when the drill string switches from being in sliding contact to rolling contact with the borehole. Once a drillstring assembly goes into rolling contact with the borehole, it rotates backwards around the center point”. Kovalyshen [20] elaborated a simple analytical model of bit whirl, taking into account the bit geometry characterized by three-dimensional parameters. Depending on their values, the analysis results have shown that the system can be stable or undergo forward or backward whirl. Spanos et al. [21] and Ritto et al. [22] underline that the uncertainty is inherent in the properties of parameters determining the drilling processes, therefore, the stochastic nature of the bit rock interaction should be taken into consideration. General questions of friction influence on deep hole drilling processes are outlined by R. Samuel [23] .
This paper is dedicated to analysis of pure rolling of the bit. Inasmuch as the constraints imposed on the system under such conditions are kinematic, it is worthwhile to apply the methods of nonholonomic mechanics for investigation of its dynamic motion. In paper [24] , on the basis of such statement of the problem, dynamics of spinning and rolling without sliding of spherical bits on spherical surfaces of bore-hole bottoms is studied. It is noted, that the bit whirl vibration can be entailed by three kinds of stable and unstable motions associated with forward and inverse rolling of the bit and its pure spinning.
As this takes place, the modes of these motions essentially depend on the DS flexibility which is determined not only by its mechanical stiffness, but also by proximity of its state to the Eulerian instability. The inference about the necessity to consider the motion of ellipsoidal bits is drawn.
However, as shown in [25] , the problem of rolling a body on an uneven plane becomes more complicated with transfer from spherical bodies to ellipsoidal ones. Nevertheless, as the bits in the shapes of elongated and oblate ellipsoids are widely used in the practice of deep drilling, the question of how their shape geometry influences on the processes of their whirling vibrations is of great interest. This question is considered below.
2. Three-Point Boundary Value Problem for Elastic Vibrations of the Lower Sections of a Drill String
To study the phenomenon of a bit rolling without sliding on a bore-hole bottom surface, it is necessary to state the problem about elastic bending vibration of the DS taking into account the constraints fulfilling the roles of boundary conditions for the dynamic equations of the DS.
Consider that it rotates with constant angular velocity ω. At its upper part, the DS is prestressed by tensile gravity force, its lower part is compressed by the contact reaction force reducing bending stiffness of the system. To enlarge this stiffness, usually centralizing devices are located in the lower segments of the DS which serve as supplemented supports. Because the most intensive bending vibrations of a DS prevail in the sections nearest to the drill bit, occurrence of the upper sections will not be taken in account and only two lower sections (segments AB and BC in Figure 1) are separated for the simulation.
Figure 1. The scheme of the drill sections separated for analysis.
Vibrations of these sections are analyzed on the basis of the theory of compressed-twisted rotating beams with internal flows of washing liquid (mud). Phenomena of torsion vibrations of rotating DSs under conditions of friction interaction between its bit and destructed rock is studied in papers [26] - [28] . Influence of internal flows of liquid on the tube rod dynamics is analyzed in [29] [30] . It is shown that these flows further the system instability.
To study elastic bending dynamics of the DS under consideration, introduce inertial coordinate system OXYZ with its origin O at the end A and axis OZ in line with the DS axis, as well as the Oxyz coordinate system rotating together with the DS tube. Let i, j, k be the unit vectors of this system.
It is assumed that the bending stress-strain state of the DS is determined by the lateral displacements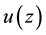 ,
, 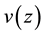 in the planes xOz, yOz of the Oxyz system.
in the planes xOz, yOz of the Oxyz system.
In the deduction of differential equations of the DS dynamics, take into account that it is prestressed by internal axial force T and torque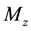 . Besides, it rotates with angular velocity ω and washing liquid moves with linear velocity v in its cavity. As a consequence, in [31] [32] , the following form of the constitutive equations was constructed.
. Besides, it rotates with angular velocity ω and washing liquid moves with linear velocity v in its cavity. As a consequence, in [31] [32] , the following form of the constitutive equations was constructed.
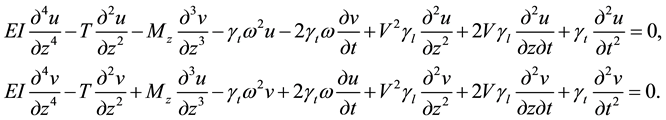 (1)
(1)
Here EI is the bending stiffness of the DS: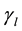 ,
, 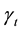 are the linear masses of the washing liquid flow and drill string tube with internal liquid, respectively; v is the velocity of the washing liquid and t is the time.
are the linear masses of the washing liquid flow and drill string tube with internal liquid, respectively; v is the velocity of the washing liquid and t is the time.
The linear masses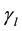 ,
, 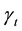 are calculated through the equalities
are calculated through the equalities
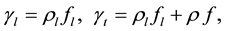 (2)
(2)
where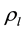 , ρ are the densities of the liquid and tube material;
, ρ are the densities of the liquid and tube material; , f are the cross-section areas of the internal channel of the DS tube and its wall, respectively.
, f are the cross-section areas of the internal channel of the DS tube and its wall, respectively.
In Equation (1), a dominant role is played by the terms with multipliers T and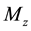 , because they influence on the Eulerian stability of the DS section and thereby determine its bending stiffness. The first ones give rise to its buckling, while the second ones lead to spiral modes of the DS deforming [32] .
, because they influence on the Eulerian stability of the DS section and thereby determine its bending stiffness. The first ones give rise to its buckling, while the second ones lead to spiral modes of the DS deforming [32] .
The roles of the members containing multipliers  and ω are less significant, because the influence of the DS rotating is essential in its long spans. Of even less importance are the terms containing the multipliers
and ω are less significant, because the influence of the DS rotating is essential in its long spans. Of even less importance are the terms containing the multipliers 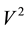 and v [31] [32] , nevertheless they are not omitted in the analysis.
and v [31] [32] , nevertheless they are not omitted in the analysis.
Equation (1) together with appropriate boundary equations at points A, B, C (Figure 1) represent the three- point boundary value problem relative to the independent variable z. To analyze whirling vibrations of the system, some initial perturbations will be imparted to it and its response to them will be studied. This part of analysis is performed on the basis of the Cauchy problem statement.
3. Statement of Boundary Conditions for the Constitutive Equations
Peculiar features of the considered problem consist in its boundary conditions. At the points A and B, they are easily formulated. At the A point positioned between the conditionally discarded upper section and one chosen for analysis, the equations
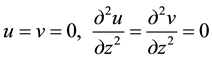 (3)
(3)
can be assumed. They correspond to the conditions of inverse symmetry of the modes of the Eulerian stability loss and free vibrations of a multispan beam.
At the B point, the equations

are valid. They stem from conditions of continuity of elastic displacement μ and v.
The boundary equations at the C point are considerably more complicated and because of this, they should be especially considered on the basis of the bit motion model.
The problem of this model creation is associated with essential theoretical and technical obstacles because many different vibration phenomena occur simultaneously in the bit dynamics, doing it difficult to isolate, evaluate, and explain any one of them. To varying degrees, axial, torsional, and bending vibrations are all present and coupled. Bit bounce, stick-slip, forward and backward whirl and linear and parametric interconnection between axial and bending vibrations all occur. Moreover, these phenomena depend on many structural, mechanical and technical parameters. Therefore, the objective of our work is to improve the understanding of the interdependence between whirling, contact cohesion of the bit with hole bottom, the bit geometry, and elastic bending pliability of the DS. However, for a real drill string configuration, the simulation results should only be interpreted in a qualitative sense.
In our work, the initial stage of the whirl proceeding is considered. Therefore, the following assumptions are used.
1) Whirl vibrations of a PDC bit is analysed. It is considered as a rigid oblong or oblate ellipsoid.
2) The bit is connected with lower sections of elastic DS. Because of this, the displacements and nutations of the bit are provoked by elastic bending and tilting of the DS.
3) Initial stage of the whirling process is considered when the point of contact of the bit with rock abandoned the hole bottom centre and moves around it, but does not achieve the hole wall. The lateral displacements of the DS are small and it does not also touch the hole wall.
The vertical force (weight-on-bit) compresses the bit to the hole bottom and thus, they are in permanent contact.
4) Angular velocity ω of the DS rotation is considered to be constant.
5) The contact interaction of the bit with the hole bottom rock is described by the Coulombic friction law [23] [25] . According to it, the friction force 

Here μ is the friction coefficient, N is the normal force of contact interaction.
Graphically, this law is represented in Figure 2, where 

Then, if the coercive forces, acting on the bit in tangential direction, are less the ultimate friction force
Figure 2. Schematic of friction force 
the bit sliding is impossible and it rolls on the bottom surface. In this case the friction force is less than the value
When the coercive forces exceed the ultimate friction force

In the proposed model, the pure rolling mechanism [7] of the bit whirling is assumed and the motion of its instantaneous centre of velocities around the hole axis [19] is analysed. The model gives the possibility to simulate the change of forward and backward whirl by each other and to explain essential enlargement of the whirl velocity in comparison with the DS rotation velocity.
Having these assumptions, it became possible to formulate equations of the body motion under action of elastic forces and moments generated at the DS end owing to contact interaction between the body and the surface.
In paper [24] , the problem on rolling of a spherical bit on a curvilinear surface is considered. As further researches of the authors demonstrated, the attempts to generalize this problem to the case of the ellipsoidal bit rolling on a curvilinear surface cause severe difficulties. For this reason, below the problem on the rotary ellipsoid bit whirling on the plane uneven surface π (Figure 1) is considered.
It is pertinent to note that the problem on ellipsoid body rolling on a plane surface has a long-standing history in the nonholonomic mechanics [25] and yet, as a rule, only its simplest versions concerning free bodies under action of gravity forces were considered and only some partial solutions were constructed. A similar situation occurs also with respect to the Celtic stones problem [1] - [4] .
In our case, the ellipsoidal bit spins relative to the axis of its symmetry and is subjected to action of the axial force t and elastic forces and moments. Besides, the equations of the bit motion do not make up constitutive equations, as in the problem on Celtic stones, but are no more than boundary conditions for the equations of the DS vibrations.
To deduce these equations detach conditionally the bit from the DS at the c point. Assume that the onset of whirling vibration is at the initial state, the bit can move in a narrow clearance without contact with the bore-hole side surface, and the bore-hole bottom is plane.
The bit motion is described by two vector equations. The first one represents the condition of kinematic compatibility of the motion velocities of the DS end and the bit body at the point of their connection. It represents the equation of nonholonomic constraint. The second equation is formulated reasoning from the condition of dynamic (in the simplified case, quasi-static) equilibrium of the elastic shear forces and moments applied to the bit.
To formulate the equations of the bit rolling, rigidly fix to it the 




In the deformed state, the 

Figure 3. Top view of the used coordinate systems.
Figure 4. The position of touch point G in the plane of ellipsoid inclination.
For the purpose of determination of the G point in the Oxyz system, introduce the right-hand coordinate system 



Then, it is possible to find the θ angle with the use of the formula

and thereafter, to calculate angle α between the planes σ and xOz:

With the aid of the introduced angle, one can find the vector ρ connecting the points C and G (Figure 4):

Here a and b are the semi-axes of the bit ellipsoid.
At the moment of the bit point G touch with the π plane, it is instantaneous centre of the bit velocities, therefore, its absolute velocity equals zero. Then [25]

where 


Considering that the bit moves in the result of the DS rotation and elastic displacement and slewing of its lower end, one has

Substituting these correlations into Equation (10) and projecting onto the axes ox and oy, one can gain the kinematic boundary conditions for the bent DS at the C point

After substitution of the components of Equation (9) for



The constraints described by these equations are nonholonomic as they are expressed through the derivatives of the unknown variables with respect to the t time [25] .
In the general case, the force boundary equations can be derived stemming from the theorem on the change of angular momentum of the bit. To exclude the unknown reaction of the contact interaction of the bit with the bore-hole bottom at the G point, it is chosen as the polar one. Then, these equations are formulated as follows:

where 


However, as shown in [24] , the mass and inertia moment of the hollow bit are small in comparison with the inertia characteristics of the drill string and for this reason they can be neglected. If so, Equation (14) is simplified

The 

and vector of elastic forces

Thef vector generates

According to Equation (15), it can be written

After corresponding substitutions and projectings, one gains from (16), (18), (19)

Taking into account Equation (9), transform Equation (20) to the form

Underline that the unknown cohesive force between the bit and bore-hole bottom is not included into these correlations. This effect is gained owing to the application of the nonholonomic approach to the problem and choice of the instantaneous centre of velocities (point G) as a polar one.
Boundary conditions (13), (21) represent the kinematic and quasi-static constraints imposed on the movement of the bit.
As a result, differential Equation (1) together with boundary conditions (3), (4), (13), and (21) make up the three-point boundary value problem for the bottom hole assembly including the bit. Its solution can be derived only by numerical methods.
4. Statement of the Cauchy Problem for the Bottom Assembly Dynamics
The above-formulated equations specify dynamic equilibrium of an ellipsoidal bit. They should be supplemented by initial conditions setting initial disturbance. Numerical solution of the stated problem is performed through the use of finite difference method with application of implicit scheme of integration in time t. To realize it, the span length l is divided into n finite difference segments 



Here

The skeleton diagrams corresponding to the finite difference operators (22) are represented in Figure 5. It is considered that in time layers j and









uations in time layer 








Figure 5. Skeleton diagrams of finite difference operators of constitutive Equation (22).
step method. The accepted approach is effective for the considered problem owing to its numerical stability in respect to non-linear systems. But it is more cumbersome in connection with the necessity to solve a system of linear algebraic equations at every step of the time increment. At the same time, this approach is less accurate in comparison with the use of the explicit finite difference scheme. So, to achieve sufficient calculating precision, it is necessary to perform calculations with rather small values of the 
5. The Simplest Schemes of Forward and Backward Whirl Rollings of Rotating Ellipsoids on an Uneven Plane
As is shown by experimental and theoretic investigations [1] - [4] , free rotating oblong ellipsoidal bodies with small geometric or mass distortions (Celtic stones) have the tendency to change the directions of their rotations. Analogous effects are typical to drill bits. They can also perform forward and backward whirlings and change their directions, describing the trajectories with the shapes of multipetal flowers cutting multilobed cross-sec- tions in bore-holes.(Thor Viggo et al. 1988), (Schen et al. 2005). But as distinguished from Celtic stones, they can have different geometry (including oblong and oblate ellipsoids, they are not free, they rotate with prescribed angular velocity
Since the objective of this work is to understand the interaction between these geometric, kinematic and structural factors, the 3D model considering coupling of the DS bending with the ellipsoidal bit, rolling on the bore-hole bottom, is reckoned to be adequate. For a real DS structure, however, the results should only be interpreted in a qualitative sense.
To reveal the basic causes influencing on the modes of the bit motion on the bore-hole bottom, consider the simplest schemes of nonholonomic rolling of a rotary ellipsoid body on an uneven plane. Let the body be attached to an elastic rod rotating with angular velocity







Kinematics of the oblate ellipsoid can be all the more complicated if the rotation axis of the deformed DS is located between the ellipsoid apex D and touch point g. Then, depending on the θ angle sign, the apex D can move in the direction of rotation while the touch point g does this in the opposite direction (Figure 6(c)), and, on the contrary, the D point can move in the rotation direction, whereas the g point does this in the opposite direction (Figure 6(d) for the backward whirl).
Thus, one can sec that depending on the shape of the bent DS, the whirling of the ellipsoidal bits can be both forward and backward, though for the oblate bits, the backward whirl is predominant.
Figure 6. Kinematic schemes of forward and backward nonholonomic rollings of ellipsoidal bodies.
The elaborated model permits us to explain one further feature of the whirling process lying in the fact that it may acquire the most destructive modes when the angular velocity of the backward whirling essentially surpasses the rate ω of the DS and amounts from 5 to 30 times the speed of the DS [19] . For the purpose of corroborating this possibility refer to Figure 6(c). At the considered instant the bit is rolling with angular velocity 



As follows from [24] , the velocity 
Then
and the angular velocity 

where d is the distance between the g point and axis OZ. It is evident that the 

Kinematics of compound motion of the bit center c becomes more evident if to study it in the rotating coordinate system Oxyz (Figure 7).
In this case, the relative velocity vector 





Figure 7. Top view of kinematic schemes of the relative velocity vector orientation.
Then the absolute velocity (

where 
Thus, if vectors 






By virtue of the fact that in actual practice the bit possessing the ellipsoidal shape is subjected to the action of forces and moments from the elastic vibrating DS, it can permanently transfer from one kinematic scheme represented in Figure 6 and Figure 7 to another, changing directions of its rotational motions, as happens with the Celtic stones. In more complex cases, when these changes of directions occur repeatedly due to elastic vibration of the DS, the trajectories of the bit centre may represent more complicated figures closely resembling multipetal flowers.
6. Simulation of Whirl Vibrations of Oblong and Oblate Ellipsoidal Bits
The elaborated techniques were used for computer simulation of whirling vibrations of DSs with elongated and oblate ellipsoidal bits. In drilling practice, a great variety of determining factors have to be considered in technological designs. They differ essentially by the bore-hole diameters (up to 40 sm), drill string materials (steel, aluminum, titanium, composite), lengths of lower spans in bottom hole assembly (range from 9 to 18 m, shapes of bits, forces on bits (up to 106 N), torques on bits (up to 104 N∙m), angular velocities of the DSs (more than 10 rad−1), and others. In our investigations, the following typical values of the characteristic parameters were chosen for the analysis: E = 2.1 × 1011 Pa, ρ = 7.8 × 103 kg/m3, ρl = 1.5 × 103 kg/m3, l = 9 m, e = 1 m, 


As shown in [24] , the whirling regimes essentially depend on bending stiffness of the DS. With its reduction, the DS becomes flexible and the bit axis acquires additional opportunities to deviate from vertical state and to begin its whirling motions. If to take into account that the DS stiffness tends to zero with its bringing nearer to Eulerian critical state, then the expediency to evaluate proximity of the DS stress-strain state to critical one becomes evident. But the task of the DS stability analysis represents a complex independent multi parametric problem because the DS is prestressed by torque and variable axial force, it rotates, mud current moves inside it, and it performs longitudinal, lateral and torsional vibrations simultaneously. Inasmuch as this problem has not general solution, it is of interest to consider some simple partial combinations of loads, permitting to assess the DS stiffness. There are two sets of the rod loadings whose critical combinations can be determined analytically. For example, consider the case when a tubular rotating pinned rod is compressed by axial force t and a liquid is flowing with velocity v inside it. Then, critical values of parameters t, V, and ω are coupled by analytical correlation [32]

Analytical solution of the Eulerian stability problem was received also for the case when the pinned rod was loaded by a torque 

So then, Eqation (25) can be used for approximate evaluation of nearness of the lower segments of the DS to the critical states when torque value is low, Equation (26) is valid when the DS rotation and mud current can be neglected.
The techniques used for analysis of equation system (1), (3), (4), (12), and (21), as stated above, represent an implicit computational algorithm of integration. It is absolutely stable for any time increment 



To actuate starting motion of the system, it was assumed that small ( 1 cm in amplitude) elastic sinusoidal bending deformations were introduced into the shapes of the two lowest sections of the DS. Next, the DS (and bit) behavior was traced.
The data of numerical analysis for the case of elongated ellipsoidal bit (a = 0.1 m, b = 0.3 m) are demonstrated in Figure 8 (ω = 5 rad/s) and Figure 9 (ω = 10 rad/s). In either example, the t forces are nearing the critical values (Tcr ≈ −7.8 × 105 N for the first example and Tcr ≈ −7.3 × 105 N for the second one).

Figure 8. Bottom view of the motion trajectories of the oblong ellipsoidal bit center c in the rotating (a) and immovable (b) coordinate systems (a = 0.1 m, b = 0.3 m, ω = 5 rad/s, T = −5.6 × 105 N, Mz = −1 × 105 N∙m).

Figure 9. Bottom view of the motion trajectories of the oblong ellipsoidal bit center C in the rotating (a) and immovable (b) coordinate systems (a = 0.1 m, b = 0.3 m, ω = 10 rad/s, T = −6 × 105 N, Mz = 0).
The trajectory in rotating coordinate system Oxyz shown in Figure 8(a) testifies that firstly the directions of the DS rotation and the bit motion were the same. But after some time, the bit began to describe very complicated curve (“to dance”, as the Celtic stones did) and then changed orientation of its motion. Complicated trajectory was also formed in the immovable coordinate system (Figure 8(b)). Its parameters are determined with the use of formulae

It can be concluded that the considered regime is unstable as the motion curves have the shapes of expanding spirals.
However, enlargement of rotation velocity ω till 10 rad/s (Figure 9) stabilizes the system motion. After some disturbance, it traces elliptic paths in the rotating reference frame (Figure 9(a)) and circles with high frequency jitter distortions in the immovable one (Figure 9(b)). This regime, though stable, is also troublesome because it is connected with large accelerations and inertia forces.
Transition from elongated bits to oblate ones leads to complication of their motions. In Figure 10 and Figure 11, the case a = 0.3 m, b = 0.1 m is represented for different values of ω, t and
Absolute motion of the oblate bit is more complicated even for small t values when its center c performs nearly stationary harmonic vibrations


Figure 10. Bottom view of the motion trajectories of the oblate ellipsoidal bit center C in the rotating (a) and immovable (b) coordinate systems (a = 0.3 m, b = 0.1 m, ω = 10 rad/s, T = −5.8 × 105 N, Mz = −1 × 105 N∙m).

Figure 11. Bottom view of the motion trajectories of the oblate ellipsoidal bit center C in the rotating (a) and immovable (b) coordinate systems (a = 0.3 m, b = 0.1 m, ω = 20 rad/s, T = −5 × 105 N, Mz = −5 × 104 N∙m).

Figure 12. Bottom view of the motion trajectories of the oblate ellipsoidal bit center C in the rotating (a) and immovable (b) coordinate systems (a = 0.3 m, b = 0.1 m, ω = 5 rad/s, T = −1 × 104 N, Mz = −1 × 104 N∙m).
absolute motion in the immovable system OXYZ is represented in Figure 12(b). It can be seen that owing to change of the bit axis orientation (as shown in Figure 6(c) and Figure 6(d)), it periodically changes directions of its velocity, resulting in generating slow and fast motions with large accelerations and inertia forces. These forces can be dangerous for strength of the bit and its diamonds.
The mode of the DS bending corresponding to the stage of comparatively slow motion is shown in Figure 13. It has a simple shape.
As noted above, the nonholonomic model advantage consists in its feature to study the bit motion without taking into consideration the cohesive force between contacting bodies. This force can be obtained from the condition of dynamic equilibrium after general solution of the stated problem. Really, the bit separated from the
elastic DS moves in the horizontal plane under action of elastic force



If the problem is solved and forces 



The 

It follows from the above-mentioned notes that the mass of the hollow bit is small in comparison with the inertia characteristics of the DS and for this reason it can be neglected. Then, the resulting cohesive force can be expressed as follows:

Shown in Figure 14 is the diagram of the 

that the axial force acting on the bit equals t = 104 N, one can infer (see Figure 2 and inequality (5)) that the regime of pure rolling without sliding can be realized if condition 
Figure 13. Modes of the DS bending in the rotating coordinate system (a = 0.3 m, b = 0.1 m, ω = 5 rad/s, T = −1 × 104 N, Mz = −1 × 104 N∙m).
Figure 14. The diagram of the cohesive force change (a = 0.3 m, b = 0.1 m, ω = 5 rad/s).
7. Conclusions
1) In the paper, the problem on rolling of a rigid ellipsoidal drill bit on a bore-hole bottom plane is stated. The bit is supposed to be attached to the lower end of an elastic rotating drill string. Two mechanical models of the bit motions based on assumption of the possibilities of its pure rolling whirling and rolling with sliding are discussed. The nonholonomic dynamic model is taken for analysis. An analogy between the phenomena of nonholonomic motions of the Celtic stones and the ellipsoidal bits is discussed. The techniques for solution of the equations of the bit whirling are proposed.
2) With the use of the elaborated approach, the computer simulation of whirling vibrations of the initially disturbed systems is performed. The oblong and oblate ellipsoidal shapes of the bits are chosen for analysis. As demonstrated by theoretic analysis of the simplest kinematic schemes of the ellipsoid bit rolling, their whirlings can be both forward and backward, though for the oblate bits, the backward whirl is predominant. As established by calculations under conditions of reduced bending stiffness of the drill string, the bit whirling can be stable as well as unstable. With the use of the simplest kinematic schemes of the ellipsoid body rolling, it is demonstrated that the oblate bits are more sensitive to initial disturbances and trajectories of their whirling paths can have loops and cuspidal points corresponding to bendings of the DSs and their bit axes tiltings these regimes are connected with enlargement of acceleration values and appropriate inertia forces.
3) The distinctive characteristic of the considered regimes is the found possibility to stop the circumferential motion of the bit whirling and to change its direction to inverse one, as happens with nonholonomic whirling of free ellipsoidal bodies with geometric or inertial distortions (the Celtic stones).
4) The elaborated techniques can be used for prediction and qualitative evaluation of the ellipsoid bit whirling regimes at the stages of the bore-hole design and drivage.
Cite this paper
Nabil W.Musa,V. I.Gulyayev,L. V.Shevchuk,HasanAldabas, (2015) Whirl Interaction of a Drill Bit with the Bore-Hole Bottom. Modern Mechanical Engineering,05,41-60. doi: 10.4236/mme.2015.53005
References
- 1. Walker, G.T. (1895) On a Curious Dynamical Property of Celts. Proceedings of the Cambridge Philosophical Society, 8, 305-306.
- 2. Walker, J. (1979) The Mysterious “Rattleback”: A Stone That Spins in One Direction and Then Reverses. Scientific American, 241, 144-149.
- 3. Lindberg, R.E. and Longman, R.W. (1983) On the Dynamic Behavior of the Wobblestone. Acta Mechanica, 49, 81-94.
http://dx.doi.org/10.1007/BF01181756 - 4. Pascal, M. (1983) Asymptotic Solution of the Equations of Motion for a Celtic Stone. Journal of Applied Mathematics and Mechanics, 47, 269-276.
http://dx.doi.org/10.1016/0021-8928(83)90016-3 - 5. Jansen, J.D. (1992) Whirl and Chaotic Motion of Stabilized Drill Collars. SPE Drilling Engineering, 7, 107-114.
http://dx.doi.org/10.2118/20930-PA - 6. Christoforou, A.P. and Yigit, A.S. (1997) Dynamic Modeling of Rotating Drillstrings with Borehole Interactions. Journal of Sound and Vibration, 206, 243-260.
http://dx.doi.org/10.1006/jsvi.1997.1091 - 7. Leine, R.I., Van Campen, D.H. and Keulties, W.J.G. (2002) Stick-Slip Whirl Interaction in Drillstring Dynamics. Journal of Vibration and Acoustics, 124, 209-220.
http://dx.doi.org/10.1115/1.1452745 - 8. Gulyaev, V.I., Khudolii, S.N. and Borshch, E.I. (2010) Whirl Vibrations of the Drillstring Bottom Hole Assembly. Strength of Materials, 42, 637-646.
http://dx.doi.org/10.1007/s11223-010-9252-y - 9. Brett, J.F., Warren, T.M. and Behr, S.M. (1990) Bit Whirl—A New Theory of PDC Bit Failure. SPE Drilling Engineering, 5, 275-281.
http://dx.doi.org/10.2118/19571-PA - 10. Langeveld, C.J. (1992) PDC Bit Dynamics. SPE/IADC Drilling Conference, New Orleans, 18-21 February 1992, 227-242.
http://dx.doi.org/10.2118/23867-ms - 11. Schen, A.E., Snell, A.D. and Stanes, B.H. (2005) Optimization of Bit Drilling Performance Using a New Small Vibration Logging Tool. SPE/IADC Drilling Conference, Amsterdam, 23-25 February 2005.
http://dx.doi.org/10.2118/92336-ms - 12. Aarrestad, T.V. and Kyllingstad, A. (1988) An Experimental and Theoretical Study of a Coupling Mechanism between Longitudinal and Torsional Drillstring Vibrations at the Bit. SPE Drilling Engineering, 3, 12-18.
http://dx.doi.org/10.2118/15563-PA - 13. Chen, S.L., Blackwood, K. and Lamine, E. (2002) Field Investigation of the Effects of Stick-Slip, Lateral, and Whirl Vibrations on Roller-Cone Bit Performance. SPE Drilling & Completion, 17, 15-20.
http://dx.doi.org/10.2118/76811-PA - 14. Wu, X., Paez, L.C., Partin, U.T. and Agnihotri, M. (2010) Decoupling Stick/Slip and Whirl to Achieve Breakthrough in Drilling Performance. IADC/SPE Drilling Conference and Exhibition, New Orleans, 2-4 February 2010.
http://dx.doi.org/10.2118/128767-ms - 15. Ledgerwood, L.W., Jain, J.R., Hoffmann, O.J. and Spencer, R.W. (2013) Downhole Measurement and Monitoring Lead to an Enhanced Understanding of Drilling Vibrations and Polycrystalline Diamond Compact Bit Damage. SPE Drilling & Completion, 28, 254-262.
http://dx.doi.org/10.2118/134488-PA - 16. Ledgerwood, L.W., Hoffmann, O.J., Jain, J.R., El Hakam, C., Herbig, C., Spencer, R.W. and Hughes, B. (2010) Downhole Vibration Measurement, Monitoring, and Modeling Reveal Stick-Slip as a Primary Cause of PDC-Bit Damage in Today’s Applications. SPE Annual Technical Conference and Exhibition, Florence, 19-22 September 2010, 2652-2661.
http://dx.doi.org/10.2118/134488-MS - 17. Sowers, S.F., Dupriest, F.E., Bailey, J.R. and Wang, L. (2009) Roller Reamers Improve Drilling Performance in Wells Limited by Bit and Bottomhole Assembly Vibrations. SPE/IADC Drilling Conference and Exhibition, Amsterdam, 17-19 March 2009.
http://dx.doi.org/10.2118/119375-ms - 18. Johnson, S.Ch. (2008) A New Method of Producing Laterally Stable PDC Drill Bits. SPE Drilling & Completion, 23, 314-324.
http://dx.doi.org/10.2118/98986-PA - 19. Stroud, D., Pagett, J. and Minett-Smith, D. (2011) Real-Time Whirl Detector Improves RSS Reliability, Drilling Efficiency. Hart Exploration & Production Magazine, 84, 42-43.
- 20. Kovalyshen, Y. (2012) A New Model of Bit Whirl. IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, Tianjin, 9-11 July 2012.
http://dx.doi.org/10.2118/156240-ms - 21. Spanos, P.D., Chevallier, A.M. and Politis, N.P. (2002) Nonlinear Stochastic Drill-String Vibrations. Journal of Vibration and Acoustics, 124, 512-518.
http://dx.doi.org/10.1115/1.1502669 - 22. Ritto, T.G., Soize, C. and Sampaio, R. (2009) Non-Linear Dynamics of a Drill-String with Uncertain Model of the Bit-Rock Interaction. International Journal of Non-Linear Mechanics, 44, 865-876.
http://dx.doi.org/10.1016/j.ijnonlinmec.2009.06.003 - 23. Samuel, R. (2010) Friction Factors: What Are They for Torque, Drag, Vibration, Bottom Hole Assembly and Transient Surge/Swab Analyses? Journal of Petroleum Science and Engineering, 73, 258-266.
http://dx.doi.org/10.1016/j.petrol.2010.07.007 - 24. Gulyayev, V.I. and Shevchuk, L.V. (2013) Nonholonomic Dynamics of Drill String Bit Whirling in a Deep Bore-Hole. Journal of Multi-Body Dynamics, 227, 234-244.
http://dx.doi.org/10.1177/1464419313482658 - 25. Neimark, Ju.I. and Fufaev, N.A. (1972) Dynamics of Nonholonomic Systems. Translation of Mathematical Monographs, 33, 519 p.
- 26. Gulyayev, V.I., Glushakova, O.V. and Hudoliy, S.N. (2010) Quantized Attractors in Wave Models of Torsion Vibrations of Deep-Hole Drill Strings. Mechanics of Solids, 45, 264-274.
http://dx.doi.org/10.3103/S0025654410020123 - 27. Gulyayev, V.I. and Glushakova, O.V. (2011) Large-Scale and Small-Scale Self-Excited Torsional Vibrations of Homogeneous and Sectional Drill Strings. Interaction and Multiscale Mechanics, 4, 291-311.
http://dx.doi.org/10.12989/imm.2011.4.4.291 - 28. Gulyayev, V.I., Hudoliy, S.N. and Glushakova, O.V. (2011) Simulation of Torsion Relaxation Auto-Oscillations of Drill String Bit with Viscous and Coulombic Friction Moment Models. Journal of Multi-Body Dynamics, 225, 139-152.
http://dx.doi.org/10.1177/1464419311405571 - 29. Gulyayev, V.I. and Tolbatov, E.Yu. (2002) Forced and Self-Excited Vibrations of Pipes Containing Mobile Boiling Fluid Clots. Journal of Sound and Vibration, 257, 425-437.
http://dx.doi.org/10.1006/jsvi.2002.5045 - 30. Gulyayev, V.I. and Tolbatov, E.Yu. (2004) Dynamics of Spiral Tubes Containing Internal Moving Masses of Boiling Liquid. Journal of Sound and Vibration, 274, 233-248.
http://dx.doi.org/10.1016/j.jsv.2003.05.013 - 31. Gulyayev, V.I. and Borshch, O.I. (2011) Free Vibrations of Drill Strings in Hyper Deep Vertical Bore-Wells. Journal of Petroleum Science and Engineering, 78, 759-764.
http://dx.doi.org/10.1016/j.petrol.2011.09.001 - 32. Gulyayev, V.I., Gaidaichuk, V.V., Solovjov, I.L. and Gorbunovich, I.V. (2009) The Buckling of Elongated Rotating Drill Strings. Journal of Petroleum Science and Engineering, 67, 140-148.
http://dx.doi.org/10.1016/j.petrol.2009.05.011
Nomenclature
a, b semiaxes of bit ellipsoid
c curvature centre of the bit surface section
e length of the 
f, fl cross-section areas of the tube wall and its internal channel
i, j, k unit vectors of the 
l length of the 
m mass of the bit
n number of finite-difference segments
r normal rodius-vector of point
t time
u, v, 



















r1, r2 external and internal radii of the drill string tube
a, b, c boundary points of the drill string spans
ab, bc upper and lower spans of the DS


d apex of the bit ellipsoid
ds drill string
ei bending stiffness of the drill string
f vector of elastic forces in the DS



g point of contact (instantaneous centre of velocities of the bit)










N normal force
O origin of the OXYZ system
Oxyz rotating coordinate system with origin O
OXYZ immovable coordinate system
OZ axis


T longitudinal compressive force in the DS

v velocity of the mud flow




























NOTES
*Corresponding author.



















