Modern Mechanical Engineering
Vol.3 No.1(2013), Article ID:28248,20 pages DOI:10.4236/mme.2013.31001
A Survey of Modeling and Control of Piezoelectric Actuators
Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, Canada
Email: jip747@mail.usask.ca
Received October 18, 2012; revised November 25, 2012; accepted December 11, 2012
Keywords: Piezoelectric Actuators; Modeling; Control
ABSTRACT
Piezoelectric actuators (PEAs) have been widely used in microand nanopositioning applications due to their fine resolution, fast responses, and large actuating forces. However, the existence of nonlinearities such as hysteresis makes modeling and control of PEAs challenging. This paper reviews the recent achievements in modeling and control of piezoelectric actuators. Specifically, various methods for modeling linear and nonlinear behaviors of PEAs, including vibration dynamics, hysteresis, and creep, are examined; and the issues involved are identified. In the control of PEAs as applied to positioning, a review of various control schemes of both model-based and non-model-based is presented along with their limitations. The challenges associated with the control problem are also discussed. This paper is concluded with the emerging issues identified in modeling and control of PEAs for future research.
1. Introduction
Piezoelectric actuators (PEAs) and PEA-driven positioning systems have been widely used in the fields of microand nanopositioning such as atomic force microscopes [1-3], adaptive optics [4], computer components [5], machine tools [6], aviation [7], internal combustion engines [8], micromanipulators [9], and synchrotron-based imaging systems [10] due to their high displacement resolution (sub nanometer) and large actuating force (typically a few hundreds of N). PEA-driven positioning systems have also been developed with various configurations, for example, 1-degree-of-freedom (1-DOF) positioning systems with flexure hinge mechanisms [11,12], stick-slip actuators [13], multiple PEAs-driven inchworms [14], or walking actuators [15]; multi-DOF positioning systems with series mechanism [16], parallel mechanism [17], or stick-and-clamping actuators [18]. In all positioning control applications, the hysteresis and creep effects of PEAs have shown to be able to significantly degrade the system performance and even system stability [19]. For improvement, models are desirable to represent these effects and on this basis, tracking controllers can be designed and implemented to achieve desired positioning requirements.
This paper reviews the modeling and control methods of PEAs in microand nanopositioning applications and some remaining issues to be solved, and is arranged as follows. Firstly, the working principles and behaviors of PEAs are briefly introduced in Section 2. In Section 3 various models and modeling techniques for PEAs are examined, along with their limitation; and in Section 4 various control schemes for PEAs are reviewed with associated challenges. Section 5 concludes with emerging issues identified in modeling and control of PEAs for future research.
2. Piezoelectric Actuators and Their Behaviors
2.1. Working Principles of Piezoelectric Actuators
PEAs utilize the converse piezoelectric effect of piezoelectric materials to generate displacement and force, i.e. a piece of piezoelectric material will be mechanically strained if subject to an electric field (by placing it into the electric field or applying voltages to its surfaces) [20]. This property is resulted from the microscopic structure of piezoelectric materials as explained in the following. Most piezoelectric materials used in PEAs, e.g. lead zirconate titanate, undergo a structural phase transition as its temperature drops through the so-called Curie temperature, during which their structurally and electrically symmetric cubic unit cells deform into structurally and electrically asymmetric tetragonal unit cells, resulting in spontaneous strain and polarization [21]. Groups of adjoining unit cells with uniformly oriented spontaneous polarization are called Weiss [20] or ferroelectric [21] domains. The directions of spontaneous polarization of different domains thus developed are random, so in this state the piezoelectric materials exhibit no overall piezoelectric behavior. To fabricate PEAs from such piezoelectric materials, they are further exposed to a strong electric field (106 to 107 V/m) at a temperature just below the Curie temperature, forcing the directions of spontaneous polarization of the domains to align with the electric field. Such alignment can be approximately preserved after the removal of the electric field. This process is referred to as poling [21,20]. After poling, due to the approximate alignment of the spontaneous polarization of the domains, the deformations of the domains in the direction of their respective spontaneous polarization resulting form the application of an voltage to the piece of piezoelectric material (which generates an electric field that either enhance or suppress the spontaneous polarization of the domains, causing their dimension to change in the direction of the spontaneous polarization) can accumulate and causes an overall deformation or displacement. Thus the piece of piezoelectric material now possesses overall piezoelectric property including the converse piezoelectric effect and can be used as a PEA [20].
2.2. Behaviors of Piezoelectric Actuators
In microand nanopositioning applications, typical behaviors of PEAs concerned include hysteresis, creep, and vibration dynamics.
Hysteresis is the nonlinear dependence of a system not only on its current input but also on its past input. In PEAs, hysteresis exists in both the electric field (voltage)-polarization relationship and the electric field (voltage)-strain (deformation or displacement) relationship, with the latter being mostly concerned in microand nanopositioning, and it is caused by the nonlinearities in the converse piezoelectric effect of the unit cells and the switching and movement of domain walls [21]. According to [22], the relationship between the actuating force exerted on the PEA and the resulting displacement of the PEA is linear, as such the electric field (voltage)-strain (displacement) hysteresis can also be treated as the result of the voltage-internal actuating force hysteresis.
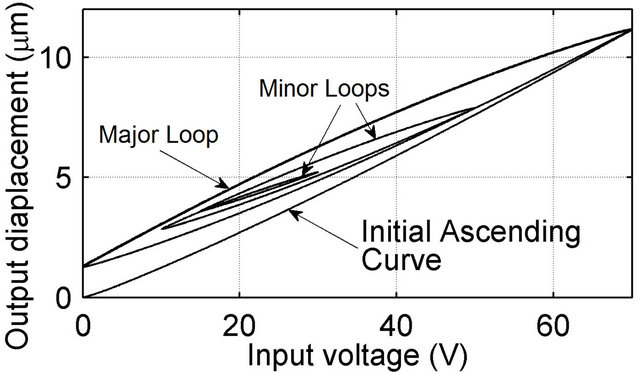
The strain (deformation or displacement)-electric field (voltage) hysteresis, which is usually also the input-output hysteresis relationship, of a typical PEA is shown in Figure 1(a). It can be seen in Figure 1(a) that the hysteresis trajectory of a PEA can be treated as being composed of three types of components: 1) the major loop which is the hysteresis loop that spans the whole input (voltage) range, 2) the minor loops which are the hysteresis loops that only span portions of the input range, and 3) the initial ascending curve which is the inputoutput trajectory traversed whenever the magnitude of the input applied to the PEA exceeds the maximum magnitude in the input history.
 (a)
(a)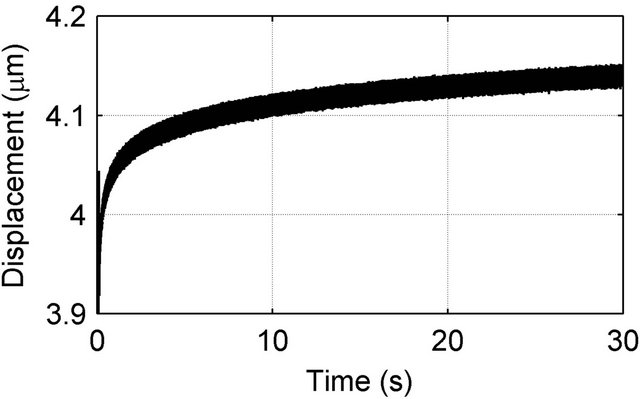 (b)
(b)
Figure 1. (a) Hysteresis of a PEA and (b) creep of a PEA subject to a 30 V step input.
Hysteresis in PEAs occurs in both relatively static operating conditions (i.e. with constant or slow varying input) and dynamic operating conditions (i.e. with fast varying input). If the influence of the rate of change of the input on the hysteresis can be ignored, then the hysteresis is referred to as rate-independent, otherwise ratedependent. The latter is usually treated as a combined effect of the rate-independent hysteresis and the vibration dynamics.
As hysteresis being the major nonlinearity of PEAs and possessing detrimental effects on the positioning accuracy and stability margins of feed-back control systems [23], compensation of hysteresis has always been a major concern in modeling and control of PEAs.
Creep is the slow variation in the PEA displacement that occurs without any accompanying change in the input voltage [24] as shown in Figure 1(b). It is caused by the same piezoelectric material properties as PEA hysteresis [20]. Being a slow and a small effect (on the order of 1% of the last displacement per time decade [20]), creep is sometimes neglected in closed loop and high frequency operations, e.g. in [25,26]. However, for slow and open-loop operations of PEAs, creep must be considered to avoid large positioning error [27].
Finally, PEAs also exhibit linear vibration dynamics, which is the dynamic relationship between the total force exerted on a PEA and the displacement of the PEA, and it resembles a distributed parameter system as the mass of the PEA is not concentrated at certain points [22]. However, if the positioning mechanism attached to the PEA, which is usually much more massive than the PEA, is also taken into account, the resulting overall vibration dynamics will approach that of a lumped parameter system [28].
3. Modeling of Piezoelectric Actuators
A large number of PEA models have been developed to mathematically represent the behaviors of PEAs mentioned in Section 2.2, and they can be generally classified into macroscopic models, which models a PEA as a whole, microscopic models, which models a PEA as a combination of a series of ferroelectric domains or discretized cells [21,29-39], and hybrid models, which combines the ideas behind these two categories has also been reported in [40]. Due to the requirement of using finite element methods, which is computationally expensive, to obtain the overall PEA behaviors, microscopic models and hybrid models are not suitable for the use in microand nanopositioning applications. As such, the following discussion only concerns macroscopic models.
The linear electromechanical model reported in [41] is an early example of macroscopic PEA models. But it can represent neither the nonlinear behaviors (hysteresis and creep) nor the linear vibration dynamics in PEAs due to its linear and static nature. To solve this, various submodels have been developed with each representing one or two of the linear/nonlinear behaviors of PEAs mentioned in Section 2.2, and then connected in appropriate manners to form (or used alone as) macroscopic PEA models. These sub-models, the methods of constructing macroscopic PEA models based on such sub-models, and the methods of inverting such sub-models for the use in model-based open-loop feedforward control of PEAs are reviewed as follows.
3.1. Hysteresis Sub-Models
3.1.1. Models for the Major Hysteresis Loop
At the early stage, hysteresis models were developed only to represent the major loop in the hysteresis trajectories of PEAs (refer to Figure 1). For example, in [42] polynomials were used to represent the major loop. The JilesAtherton hysteresis model, which was initially developed for representing ferromagnetic hysteresis [43] and afterwards adopted for the ferroelectric hysteresis in piezoelectric materials [44], is also limited to represent the major loop [45]. The inability of such models to represent minor loops in the hysteresis curves of PEAs limits their applications.
3.1.2. Rate-Independent Hysteresis Models
To model both the major loops and the minor loops in the hysteresis of PEAs without concerning the influence of the rate of chance of the input, in other words, to model the rate-independent hysteresis of PEAs, both existing and newly developed rate-independent hysteresis models have been adopted. Among which the Preisach hysteresis model [46] and its modifications [47-58], the PrandtlIshlinskii (PI) hysteresis model [25,59-63], and the Maxwell resistive capacitor (MRC) model [64-67] are among the most widely used. These rate-independent hysteresis models are reviewed as follows.
The Preisach hysteresis model represents the hysteresis by the combined effect of an infinite number of Preisach hysteresis operators , as shown in Figure 2. Two parameters are used to characterize a Preisach hysteresis operator: the up switching value
, as shown in Figure 2. Two parameters are used to characterize a Preisach hysteresis operator: the up switching value  and the down switching value
and the down switching value , with
, with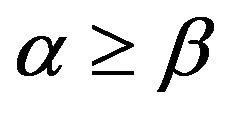 . Each operator has two saturation values: 0 and 1, and its contribution to the model output is adjusted by
. Each operator has two saturation values: 0 and 1, and its contribution to the model output is adjusted by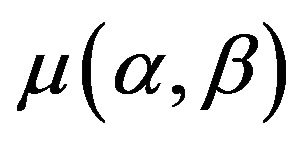 , referred to as the Preisach weighting function. As such, the resulting Preisach hysteresis model is expressed as
, referred to as the Preisach weighting function. As such, the resulting Preisach hysteresis model is expressed as
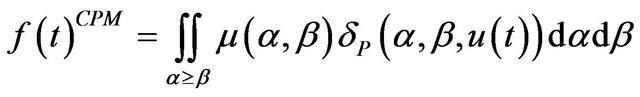 (1)
(1)
 (a)
(a)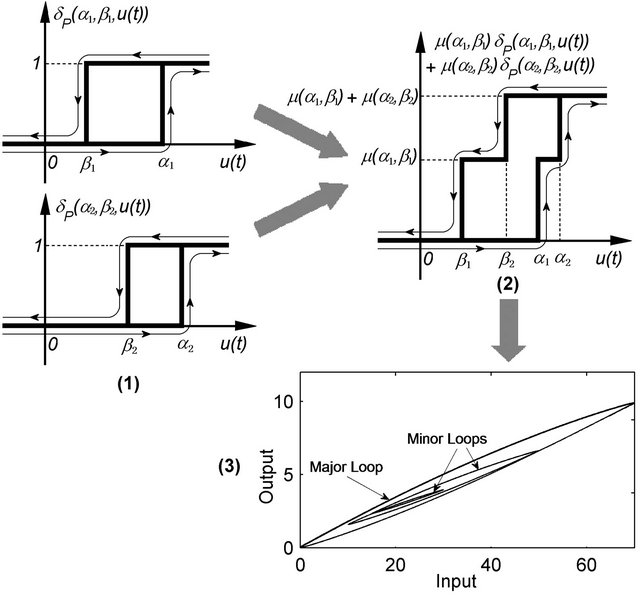 (b)
(b)
Figure 2. (a) Preisach hysteresis operator and (b) working principle of the Preisach hysteresis model: the sum of two hysteresis operators of different switching values as shown in (1) can represent a simple but unsmooth hysteresis loop as shown in (2); by using the sum of an infinite number of hysteresis operators of different switching values, smooth hysteresis loops including both major and minor loops can then be represented as shown in (3).
where 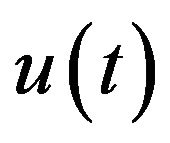 is the input and
is the input and 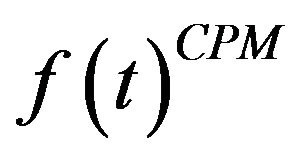 is the output of the hysteretic system [47]. To reduce the computational effort due to the involvement of the double integration, alternative expressions of the Preisach hysteresis model that only involves arithmetic operations have also been derived from Equation (1) and the properties of the Preisach hysteresis operator [68,69].
is the output of the hysteretic system [47]. To reduce the computational effort due to the involvement of the double integration, alternative expressions of the Preisach hysteresis model that only involves arithmetic operations have also been derived from Equation (1) and the properties of the Preisach hysteresis operator [68,69].
In PI hysteresis models, hysteresis is represented by the combined effect of a finite number of play or backlash operators as shown in Figure 3. Following this idea, the expression of a PI hysteresis model involving 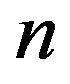 play operators is given as
play operators is given as
 (2)
(2)
where  is the model output;
is the model output; 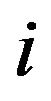 denotes the index of the play operator;
denotes the index of the play operator; 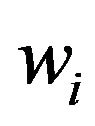 and
and 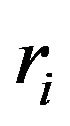 are the weight parameter and the threshold parameter of the i-th play operator, respectively.
are the weight parameter and the threshold parameter of the i-th play operator, respectively.
Similar to the PI hysteresis model, the MRC hysteresis model represents the hysteresis by the combined effect of a finite number of elasto-slide elements or operators as shown in Figure 4 [64]. Each elasto-slide element or operator (Figure 4(a)(1)) is composed of 1) a mass sliding on a surface with a Coulomb friction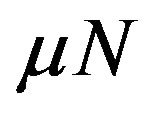 , where
, where  is the friction coefficient and
is the friction coefficient and 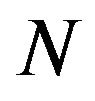 is the normal force between the mass and the surface, and 2) a spring of stiffness
is the normal force between the mass and the surface, and 2) a spring of stiffness 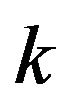 with one end connected to the mass whilst
with one end connected to the mass whilst
 (a)
(a) (b)
(b)
Figure 3. (a) Play operator and (b) working principle of the PI hysteresis model: the sum of two play operators of different parameters as shown in (1) form a simple PI hysteresis model as shown in (2).
 (a)
(a)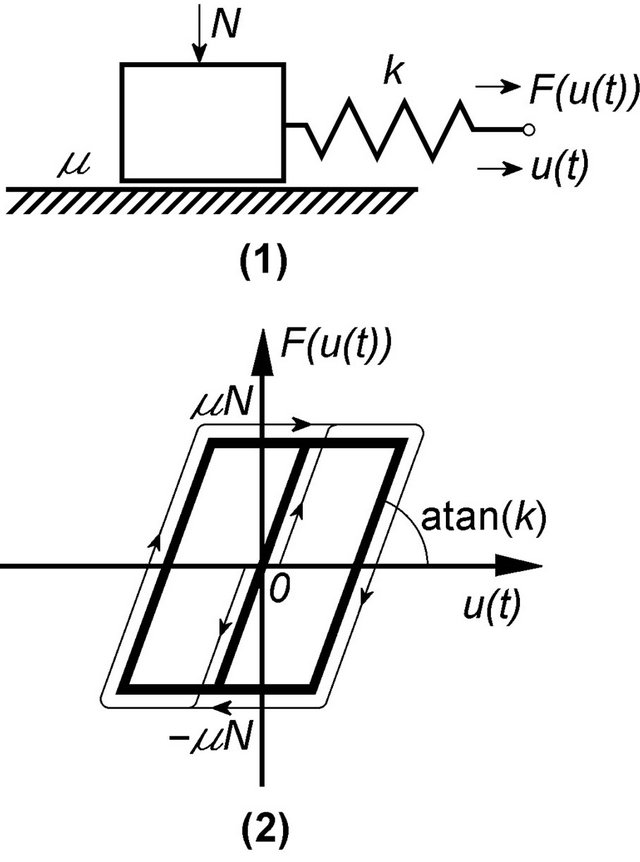 (b)
(b)
Figure 4. (a) An elasto-slide element and its input-output relationship; (b) The physical interpretation of the MRC hysteresis model [63].
the displacement of the other end (the free end)  can be freely assigned and use as input to the elasto-slide element. As such, hysteresis relationship exists between the (input) displacement of the free end of the spring
can be freely assigned and use as input to the elasto-slide element. As such, hysteresis relationship exists between the (input) displacement of the free end of the spring  and the resulting force in the spring
and the resulting force in the spring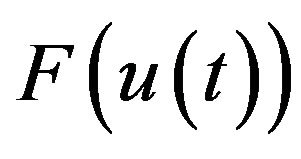 , as can be seen in Figure 4(a)(2).
, as can be seen in Figure 4(a)(2).
Connecting  elasto-slide elements as in Figure 4(b), the resulting MRC hysteresis model or the relationship between the input displacement of the free ends of the springs
elasto-slide elements as in Figure 4(b), the resulting MRC hysteresis model or the relationship between the input displacement of the free ends of the springs  and the total force experienced at the free ends of the springs
and the total force experienced at the free ends of the springs  can be expressed as
can be expressed as
 (3)
(3)
where  is the force in the spring of the i-th elasto-slide element induced by
is the force in the spring of the i-th elasto-slide element induced by .
.
3.1.3. Rate-Dependent Preisach and PI Hysteresis Models
The rate-independent hysteresis models discussed in Section 3.1.2 are only capable of representing the hysteretic behavior of a PEA in narrow (a few Hz) frequencies bands. In wide band applications where both hysteresis and vibration dynamics are significant, the rate-independent hysteresis models need either to be combined with vibration dynamics models or to be modified into rate-dependent hysteresis models to represent the behaviors of the PEA. In the literature, both the Preisach hysteresis model and the PI hysteresis model have been modified into rate-dependent hysteresis models.
In the rate-dependent Preisach hysteresis models, the Preisach weighting function 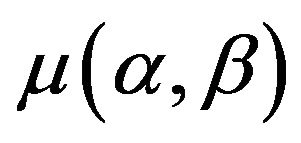 are adjusted to account for the input-rate dependency by using rate-dependent multiplicative modifying factors [68,70] or neural network approaches [69]. In [68], the rate-dependent multiplicative modifying factor for adjusting
are adjusted to account for the input-rate dependency by using rate-dependent multiplicative modifying factors [68,70] or neural network approaches [69]. In [68], the rate-dependent multiplicative modifying factor for adjusting  is a function of 1) the average voltage input rate between two input extrema and 2) the variation of the voltage between two input extrema. Even though this model can effectively represent the PEA hysteresis up to 800 Hz, it requires the a priori knowledge of the input voltage waveform (at least to the next extremum), and thus being not applicable to conventional situations in which the future input voltage is unknown. To avoid this problem, in [70] a multiplicative modifying factor which depends only on the input-rate or the first derivative of the input voltage is used instead. However, the small differences between the input-rate at the input extrema at different input frequencies limits the model accuracy at higher input frequencies (the model is effective typically below 10 Hz). To achieve better accuracy (error of the model prediction being less than 5% of the maximum displacement of the PEA) in operations involving higher frequencies (~30 Hz), in [69] a neural network with rate-dependent output is used to account for the input-rate dependence of the Preisach weighting function. But the applicable frequency range remains low compared to the resonant frequencies of conventional PEAs (typically over 1 KHz).
is a function of 1) the average voltage input rate between two input extrema and 2) the variation of the voltage between two input extrema. Even though this model can effectively represent the PEA hysteresis up to 800 Hz, it requires the a priori knowledge of the input voltage waveform (at least to the next extremum), and thus being not applicable to conventional situations in which the future input voltage is unknown. To avoid this problem, in [70] a multiplicative modifying factor which depends only on the input-rate or the first derivative of the input voltage is used instead. However, the small differences between the input-rate at the input extrema at different input frequencies limits the model accuracy at higher input frequencies (the model is effective typically below 10 Hz). To achieve better accuracy (error of the model prediction being less than 5% of the maximum displacement of the PEA) in operations involving higher frequencies (~30 Hz), in [69] a neural network with rate-dependent output is used to account for the input-rate dependence of the Preisach weighting function. But the applicable frequency range remains low compared to the resonant frequencies of conventional PEAs (typically over 1 KHz).
Similarly, the rate-dependent PI hysteresis models, which are modified from the PI models by modeling the parameters as functions of the input rate, are also limited to represent low frequency (<30 Hz) PEA operations or the error becomes excessively high (over 10% of the peak-to-peak sinusoidal displacement of the PEA) [25,26].
So, in conventional applications where the a priori knowledge of the input voltage is not available, the ratedependent Preisach and the rate-dependent PI hysteresis models are both limited to represent PEA operations over frequency bands only slightly wider than the applicable frequency bands of the rate-independent models.
3.1.4. Inverse Preisach and PI Hysteresis Models
Inverse hysteresis models are essential to the modelinversion-based feedforward hysteresis compensation technique for PEAs. The inverses of the two most widely used hysteresis models, i.e. the Preisach hysteresis model and the PI hysteresis model, have been established by employing different methods in the literature.
The Preisach hysteresis model cannot be inversed analytically; hence several methods of approximately inverting the Preisach hysteresis model have been developed instead [71]. Such approximate inverting methods can be classified into two categories.
The first category involves directly identifying the Preisach hysteresis model inversely (using the measured plant output as the input to the Preisach hysteresis model while using the plant input as the output to the Preisach hysteresis model) [1,72,73] or directly identifying the inverses of some intermediate functions that constitute the alternative expressions of the Preisach hysteresis model and then expressing the inverse Preisach hysteresis model based on them [56,71]. The advantage of this category of methods is that the computational effort of the inverse Preisach hysteresis model is the same as the Preisach hysteresis model, not more. However, in applications that also require the Preisach hysteresis model in additional to the inverse one, a different parameter identification procedure has to be performed (assume without using iterative methods) since the former can not be analytically derived from the latter, and the two resulting models are not necessarily accurate inversions of each other due to the different model errors introduced in their respective parameter identification procedures.
The second category involves iterative-algorithms-based methods [71], which find the input to an identified Preisach hysteresis model iteratively until the output of the hysteresis model converges to the desired value. Such methods are developed based on the contraction mapping principle, which are firstly proposed in [74,75], and they have been successfully applied to inverse the Preisach hysteresis modeled hysteresis in a magnetostrictive actuator [71] and a PEA [76]. The advantage of such methods is that both the Preisach hysteresis model and the inverse one can be obtained via a single parameter identification procedure and the inversion can be highly accurate. However, the computational effort involved in the iterative-algorithms-based methods is generally much higher than that of calculating the Preisach hysteresis model output since the Preisach hysteresis model output needs to the calculated in each iteration.
The PI hysteresis model, in the contrary, can be inversed analytically, so good accuracy and low computational effort can be achieved simultaneously, making it much easier to implement than the inverse Preisach hysteresis models. The inversion algorithms for PI hysteresis models can be found, for example, in [63]. In [25,26] the inversion of the rate-dependent PI hysteresis model was also presented. In either case of rate-independent or rate-dependent, the PI hysteresis model inversion algorithms fail if the input frequency is so high that the rounding of the hysteresis loops due to phase lag introduced by other dynamics causes the hysteresis loading and unloading curves to be no longer monotonic. This problem was later solved in [77] by additional mappings to and back from a domain where the inversion of the rate-dependent PI hysteresis model always exists.
3.1.5. Other Hysteresis Models
Other hysteresis models, such as a first-order nonlinear differential equation model [78] and the Bouc-Wen hysteresis model [79-81] have also been used to model hysteresis in PEAs with promising results [22,82-84]. In [85], a non-linear auto-regressive moving average model with exogenous inputs (NARMAX) was employed to represent the hysteresis of a PEA. In [73] a hysteresis model was developed for PEAs by using a polynomialbased linear mapping strategy. In [86], a hysteresis model based on a new hysteresis operator, which in turn is based on two hyperbola functions, are developed for PEAs along with its inverse model. Such hysteresis models have not seen wide application mainly due to their high complexity but limited improvements on accuracy as compared to other widely used hysteresis models discussed before.
3.2. Creep Sub-Models
3.2.1. Frequently Used Creep Models
The creep response in a PEA has a logarithmic shape over time, so it is sometimes referred to as the Log(t)- type creep, and the nonlinear creep model given by Equation (4) has been used to represent such creep behavior [87,88].
 (4)
(4)
where  is the creep model output,
is the creep model output,  is the creep output at
is the creep output at 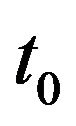 after the static input voltage is applied, and
after the static input voltage is applied, and 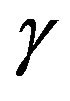 is a coefficient depending on the input voltage. The dependence of
is a coefficient depending on the input voltage. The dependence of  on the input voltage and the unboundness of such a nonlinear creep model as
on the input voltage and the unboundness of such a nonlinear creep model as 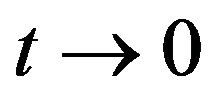 and
and  pose difficulties in its implementation [19].
pose difficulties in its implementation [19].
To avoid the problem of unboundness encountered in the nonlinear creep model Equation (4) and to avoid the nonlinearity, a linear creep model was proposed as.
 (5)
(5)
where the creep transfer function  is represented by the combined effects of
is represented by the combined effects of 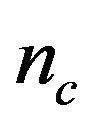 spring
spring 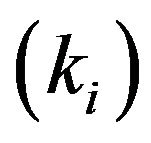 damper
damper  systems [1,88]. Besides, an operator-based linear creep model was also reported in [60]. However, these linear creep models have linear and memory free equilibrium values, whist the actual equilibrium value of the creep effect of PEA exhibits hysteresis nonlinearity [89].
systems [1,88]. Besides, an operator-based linear creep model was also reported in [60]. However, these linear creep models have linear and memory free equilibrium values, whist the actual equilibrium value of the creep effect of PEA exhibits hysteresis nonlinearity [89].
To further solve the problems encountered in both the nonlinear and linear creep model above, the PI hysteresis model design approach was adopted in [63] to develop an operator-based nonlinear creep model, whose output is a weighted sum of the values of a series of elementary creep operators.
3.2.2. Inverse Creep Models
Similar to the case of inverse hysteresis models, inverse creep models are essential in feedforward creep compensation.
While the analytic inversion of the nonlinear creep model was not mentioned in the literature, a method of feeding a voltage with an inverse Log(t)-type creep itself to a PEA to compensate for the creep in the output displacement was found to be effective [87].
On the other hand, the inversion of the linear creep model (Equation (5), not operator-based) is usually carried out together with the inversion of the vibration dynamics model since they can be combined into a single linear dynamics model. An optimal inversion approach, which minimizes a quadratic cost function representing the weighted sum of the input voltage energy and the output displacement error energy [90], can be used to inverse the combined vibration dynamics and creep model in [1]. Linear creep models can also be combined with hysteresis models and then inverted, e.g. via iterative methods [88].
The inversion of the operator-based linear and nonlinear creep models together with other dynamics are reported in [60,63], respectively.
3.3. Vibration Dynamics Sub-Models
3.3.1. Frequently Used Vibration Dynamics Sub-Models
According to Section 2.2, for the consideration of accuracy, the vibration dynamics of a PEA should be modeled as a distributed linear system for a stand-alone PEA [22]. But for the convenience of practical uses, the vibration dynamics of a PEA and the attached positioning mechanism is often modeled as a whole as a single second-order system, as in [28,64,91,92], whilst higher order linear dynamical systems are only used in applications requiring higher level of accuracy [1]. Such lumped linear vibration dynamics models of PEAs are usually identified through fitting the measured frequency response of the PEA to that of a specific model structure by using a dynamic signal analyzer [1,93]. On the other hand, the axiomatic design method has also been used to find a higher order linear system representation of the vibration dynamics of a PEA with an attached positioning mechanism [94,95].
3.3.2. Inverse Vibration Dynamics Sub-Models
Inverse vibration dynamics are usually used in open-loop feedforward control of PEAs, especially in the case of controlling piezoelectric tube actuators as in [1]. Methods for inverting the vibration dynamics have been reviewed in Section 3.2.2.
3.4. Model Structures
With different sub-models representing hysteresis, creep, and vibration dynamics of PEAs defined, macroscopic PEA models are constructed by connecting such submodels according to certain model structures. There are two categories of model structures for macroscopic PEA models.
In the first category, the behavior of a PEA, when subject to a voltage input and an external loading force, is decoupled into several effects such as rate-independent hysteresis, vibration dynamics, and creep based on physical laws. Such effects are then represented by individual sub-models and such sub-models are connected in various manners to form a comprehensive model of the PEA.
The most well known model structure of PEAs belonging to this category is the electromechanical model proposed in [64], which is further refined in [22]. Figure 5 shows the schematic representation of this model.
There are 3 effects in Figure 5, namely 1) the hysteresis,  , between the charge in the PEA,
, between the charge in the PEA, 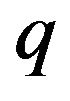 , and the resulting voltage,
, and the resulting voltage,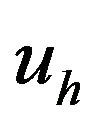 ; 2) the electromechanical transducer,
; 2) the electromechanical transducer,  , converts the mechanical deformation of the PEA,
, converts the mechanical deformation of the PEA, 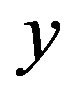 , into charge, (inverse piezoelectric effect), and converts the voltage,
, into charge, (inverse piezoelectric effect), and converts the voltage,  , into an actuating force,
, into an actuating force,  (piezoelectric effect); and 3) the vibration dynamics,
(piezoelectric effect); and 3) the vibration dynamics,  , relating the deformation of the PEA,
, relating the deformation of the PEA, 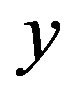 , to the internal actuating force,
, to the internal actuating force, 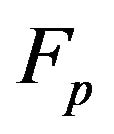 , and the external load,
, and the external load,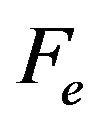 . Other symbols in Figure 5 include
. Other symbols in Figure 5 include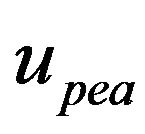 , which is the voltage across the PEA,
, which is the voltage across the PEA, 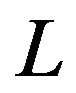 , which is the original length of the PEA, and
, which is the original length of the PEA, and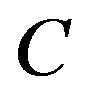 , which is the capacitance of the PEA. The model can then be expressed as
, which is the capacitance of the PEA. The model can then be expressed as
 (6)
(6)
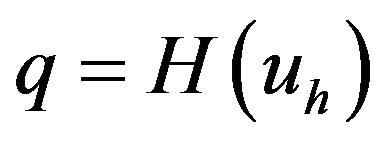 (7)
(7)
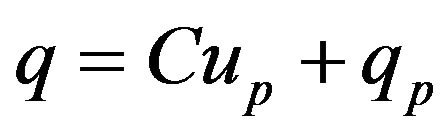 (8)
(8)
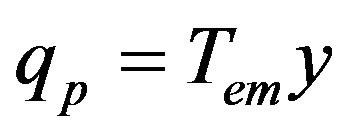 (9)
(9)
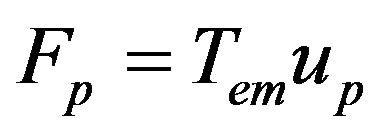 (10)
(10)
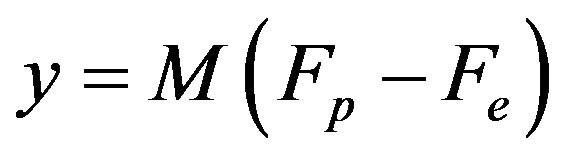 (11)
(11)
The hysteresis effect,  , and the vibration dynamics,
, and the vibration dynamics, 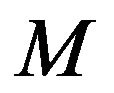 , can be modeled by different kinds of sub-models. Specifically,
, can be modeled by different kinds of sub-models. Specifically,  is usually represented by rate-indepen-
is usually represented by rate-indepen-

Figure 5. Schematic representation of a electromechanical model of a PEA [22].
dent hysteresis models, e.g. the MRC model was used in [64] whist the first-order nonlinear differential equation model, which was firstly proposed in [78], was employed in [22]. The vibration dynamics,  , can be modeled by any models discussed in Section 2.1.3. It is noted that the use of this electromechanical model usually requires the measurements of the charge,
, can be modeled by any models discussed in Section 2.1.3. It is noted that the use of this electromechanical model usually requires the measurements of the charge, 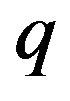 , in the PEA for model parameter estimation, which is difficult in practice. So this model is usually employed in applications that the relationship between
, in the PEA for model parameter estimation, which is difficult in practice. So this model is usually employed in applications that the relationship between 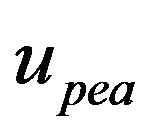 and
and , which is difficult to identify, can be approximated by a simple function (e.g. an affine function) with an error term as model uncertainties, such as in [91,92]. Also, creep is usually not considered in this electromechanical model [22,78] expect being treated as model uncertainties [91,92].
, which is difficult to identify, can be approximated by a simple function (e.g. an affine function) with an error term as model uncertainties, such as in [91,92]. Also, creep is usually not considered in this electromechanical model [22,78] expect being treated as model uncertainties [91,92].
Another model structure proposed in [1] models the relationship between 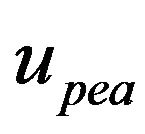 and
and 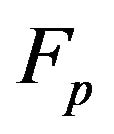 by a rate-independent hysteresis model directly, based on a conclusion drawn from the analysis in [64] that the rate-independent hysteresis of a PEA only exists between the input voltage and the resulting internal actuating force. This hysteresis sub-model is then cascaded to a vibration dynamic submodel and a creep sub-model to form the complete model of a PEA, as shown in Figure 6. Without the involvement of charge measurement for parameter estimation, this model structure is much easier to apply than the electromechanical model. Similar to the case of the electromechanical model, this model structure is highly flexible that each sub-model can be implemented in various ways, e.g. in [1], the Preisach hysteresis model was used for
by a rate-independent hysteresis model directly, based on a conclusion drawn from the analysis in [64] that the rate-independent hysteresis of a PEA only exists between the input voltage and the resulting internal actuating force. This hysteresis sub-model is then cascaded to a vibration dynamic submodel and a creep sub-model to form the complete model of a PEA, as shown in Figure 6. Without the involvement of charge measurement for parameter estimation, this model structure is much easier to apply than the electromechanical model. Similar to the case of the electromechanical model, this model structure is highly flexible that each sub-model can be implemented in various ways, e.g. in [1], the Preisach hysteresis model was used for  and a fourth-order and a third-order linear dynamic systems are used to represent
and a fourth-order and a third-order linear dynamic systems are used to represent 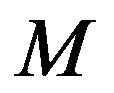 and the creep effect,
and the creep effect,  , whist in [63], a modified PI hysteresis model is used for
, whist in [63], a modified PI hysteresis model is used for  and an operator based model of complex Log(t)- type creep for
and an operator based model of complex Log(t)- type creep for . Also, due to the cascading connection between the sub-models, this model structure is very suitable for implementing control schemes with inverse nonlinearity and/or vibration dynamics compensation as in [1,63,93,96,97]. A similar model structure constructed using a bond-graph representation was also presented in [67].
. Also, due to the cascading connection between the sub-models, this model structure is very suitable for implementing control schemes with inverse nonlinearity and/or vibration dynamics compensation as in [1,63,93,96,97]. A similar model structure constructed using a bond-graph representation was also presented in [67].
In the second category, the different behaviors of a PEA are not decoupled. In such cases, rate-dependent hysteresis models such as the rate-dependent Preisach hysteresis model, the rate-dependent PI hysteresis model (Section 3.1.3), and the rate-dependent neural-networkbased hysteresis model [98] are used directly as models of the PEA. However, as mentioned in Section 3.1.3,
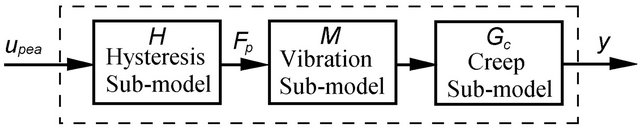
Figure 6. Model structure of a PEA as in [1].
such models are only accurate over small frequency ranges. And, as can be seen above, creep is usually neglected. These disadvantages seriously limit their usage.
4. Control of PEAs
Over the years, a number of control schemes have been reported for positioning control of PEAs. Due to the detrimental effects of the nonlinearities (especially hysteresis) of PEAs on positioning control performances in terms of positioning error and stability [19], the compensation or rejection of such nonlinear effects has been a major consideration in all of these control schemes. In the following, the typical control schemes for PEAs are reviewed.
4.1. Open-Loop Control Schemes
Open-loop control schemes are usually employed in applications in which position feedback are difficult to implement due to mechanical constraints, e.g. atomic force microscopes [1-3]. In such control schemes, inverse model of the PEA to be controlled is found and then cascaded to the PEA. The methods for finding such inverse models have been reviewed in Sections 3.1.4, 3.2.2, and 3.3.2. The inverse model generates an input voltage  to the PEA according to the desired displacement
to the PEA according to the desired displacement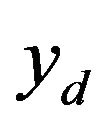 , such that the PEA subject to
, such that the PEA subject to  produces an output displacement of PEA
produces an output displacement of PEA  that follows
that follows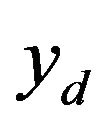 . Figure 7 shows a typical open-loop control scheme for PEAs.
. Figure 7 shows a typical open-loop control scheme for PEAs.
In some of the open-loop control schemes, all three effects in the PEA shown in Figure 6 are compensated for by the inverse model of PEA to achieve best tracking accuracy (as the case in Figure 7). For example, in [1,67], inverse models of PEA representing hysteresis, vibration dynamics, and creep are used to compensate for these effects; whist in [93] a charge control technique was firstly employed to remove the hysteresis effect and then an inverse model was used to compensate for the linear dynamics.
Other open-loop control schemes only focus on compensating for some of the three effects shown in Figure 6. For example, in [72,73,86,99], only hysteresis was compensated for by using the inverses of the Preisach hy-

Figure 7. Open-loop control scheme for a PEA [1].
steresis model, a hysteresis model developed by using a polynomial-based linear mapping strategy, a hysteresis model developed based on hyperbola-shaped hysteresis operators, and a hysteresis model developed in [100], respectively, since hysteresis is the most significant nonlinearity in PEAs. In [90,101], creep is also compensated for in additional to hysteresis by using operator-based inverse creep models and inverse PI hysteresis models to achieve better tracking performance. However, due to the negligence of the vibration dynamics in these schemes, their performances are only guaranteed in fixed frequency or narrow band operations unless inverse ratedependent hysteresis models are employed, e.g. the use of inverse rate-dependent PI hysteresis models in [25,26,77]. Nonetheless, the applicable frequency ranges (with acceptable tracking error, e.g. <5% of the maximum displacement of the PEA) of the schemes using inverse ratedependent hysteresis models are still relatively small (less than 50 Hz) compared with those also inverting the vibration dynamics (up to a few hundreds of Hz) [1,25,77].
In no load condition the open-loop control schemes have been shown to be highly effective in their applicable frequency ranges [1].
However, one major disadvantage of the open-loop control schemes is that their positioning performances are highly sensitive to unknown effects such as model errors, external loads, and changes in the dynamics of the PEA. To partially alleviate the problem, reference [65] proposed to use a disturbance-observer-based scheme in addition to the inverse MRC hysteresis model to compensate for the hysteresis and unknown effects simultaneously. Specifically, the estimated disturbance input to the PEA, which has the same effect as the aforementioned unknown effects on the PEA output, is subtracted from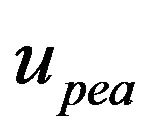 . However, the effectiveness of this scheme was not examined through experiments. In [102], the inverse hysteresis model is updated adaptively to account for the unknown effects. However, the influence of the unknown effects on the PEA output, though largely suppressed, can still be clearly observed in the experiment results. As such, the best solution to this problem remains introducing feedback into the control schemes, which is to be discussed in the following sections.
. However, the effectiveness of this scheme was not examined through experiments. In [102], the inverse hysteresis model is updated adaptively to account for the unknown effects. However, the influence of the unknown effects on the PEA output, though largely suppressed, can still be clearly observed in the experiment results. As such, the best solution to this problem remains introducing feedback into the control schemes, which is to be discussed in the following sections.
4.2. Feedback
Feedback control schemes as shown in Figure 8 lead to strong suppression of the unknown effects including model errors, external loads, and changes in the dynamics of the PEA on the position control performances, hence they are widely used.
In static or low frequency operations, classical control techniques such as PID control or using multiple integrators for tracking desired displacement profiles are widely used because of their simplicity and capability of elimi-

Figure 8. A feedback control scheme for PEAs [19].
nating steady state errors in such applications [20,103,104]. Various PID tuning techniques has been reported in PEA positioning control applications, e.g. by trial and error [20], by grey relational analysis [105], using an optimal linear quadratic regulation method [106], by a semiautomatic tuning technique [107], and by an automatic tuning technique [108]. However, in broadband operations with large system uncertainties including modeling errors, nonlinearities, external loads, etc., advanced control techniques are required because PID control is limited in bandwidth while dealing with uncertainties [109].
Among all of such advanced control techniques, sliding mode control has drawn a lot of attention in the recent years. This is due to the fact that sliding mode controllers can completely reject the effects of the so-call matched uncertainties or uncertainties in the input channel of the plant, resulting in strong robustness [110].
Specifically, in its basic form, the control signal generated by a sliding mode controller can be divided into two parts. The first part is discontinuous, referred to as the switching control, for compensating for the matched uncertainties while driving the plant trajectory to a prescribed geometric entity in the phase space (a space with each dimension corresponding to one state variable in the plant model), referred to as the sliding surface. The second part is continuous, referred to as the equivalent control, for keeping the plant trajectory on the sliding surface after the latter is reached. Since the sliding surface and hence the closed loop system dynamics after reaching the sliding surface can be freely designed, the closedloop system becomes insensitive to the matched uncertainties after the sliding surface is reached [110]. The major problem of implementing the sliding mode control techniques on PEAs is chattering and the need of the knowledge about the bounds of the matched uncertainties for designing the discontinuous control signal [110], which is to be discussed in more detail in Section 5.2.
Based on the model structure shown in Figure 6, hysteresis and creep in a PEA can be treated as (matched) uncertainties in the input channels of the vibration dynamics sub-model of the PEA (given that a linear creep model is used). As such, a sliding mode controller can be designed using the vibration dynamics sub-model as a nominal model of the PEA, and the effects of hysteresis and creep on the PEA output displacement can be strongly suppressed without knowing the exact expression of the hysteresis sub-model and the creep sub-model, thus largely reducing the efforts involved in hysteresis and creep modeling and compensation [95,111-114]. Various modifications of the basic sliding mode control technique have also been reported for controlling PEAs for improved performance. For instance, adaptive methods are combined with sliding mode control to remove the requirement of model parameter estimation or lead to better compensation for the nonlinearities as in [115-117]. And in [118] the nonlinearities of the positioning mechanism driven by a PEA in additional to those of the PEA itself were considered in sliding mode controller design.
Robust control techniques constitute another branch of widely used advanced control techniques for positioning control of PEAs. They try to find the control law via optimizing an objective function that incorporates the robustness objective, for example, minimizing the H∞ norm [88,119-122] or the H2 norm [76] of the transfer functions relating the disturbances to the plant output, thus minimizing the effects of the disturbances on the plant output and enhancing robustness. Robust control techniques can be combined with sliding mode control to suppress unmatched uncertainties (which the sliding mode control techniques cannot compensate for), while sliding mode control are considered to be superior in dealing with matched uncertainties because robust control techniques can only minimize the effects of the matched uncertainties on the plant output whilst sliding mode control techniques can completely reject such effects in theory [110].
Other advanced control techniques such as state feedback [123], optimal control [109,124], adaptive control [125-128], and neuron network methods [129-131] have also been applied to control PEAs.
Inverse sub-models of the nonlinearities of PEA are sometimes inserted between the feedback controller and the controller in Figure 8 to linearize the PEA thus facilitating the use of linear feedback controllers. For example, an inverse Preisach hysteresis model is used to cancel out the hysteresis and then a linear H2 controller is designed based on the remaining linear dynamics of a PEA in [76], while an inverse PI hysteresis model and a sliding mode controller are used in [113].
One problem with the feedback control schemes for PEAs is that the resulting closed-loop systems have low gain margins, which limit the use of high gain controllers. Such low gain margin is largely due to the quick phase loss near the first resonant peak in the frequency response of a PEA [23]. This problem can be alleviated by using a notch filter to reduce the gain around the first resonant peak [20,132,133].
4.3. Feedback with Feedforward
Feedforward is sometimes used to augment feedback controllers for nonlinearity compensation. A typical control scheme of this type is shown in Figure 9. An advantage of this scheme is that the low gain margin problem
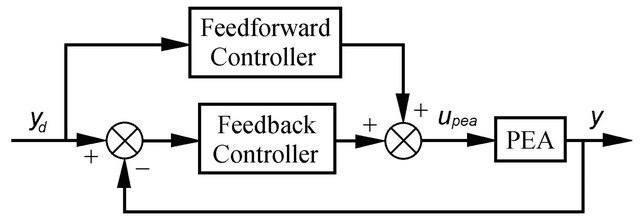
Figure 9. A feedback augmented with feedforward control scheme for PEAs [19].
can be alleviated such that high frequency positioning performances can be improved over the feedback control schemes [124,134,135]. Recent researches adopting this scheme can be found, e.g. in [136] a hysteresis compensator based on the inverse Preisach hysteresis model was used as the feedforward controller to compensate for hysteresis whist a PID feedback controller was used to account for other effects, in [137] a inverse nonlinear differential equation hysteresis model was used as the feedforward controller and a PI controller was used as a feedback controller, and in [16] a inverse extended Coleman-Hodgdon model was used as the feedforward controller and a feedback controller designed via loop shaping techniques was employed.
Another control scheme involving feedback and inverse model feedforward is shown in Figure 10 [97,138]. In this scheme, the feedback controller is a high gain controller used for nonlinear effect suppression such that the closed loop system has linear dynamics. Then a feedforward controller, which is the inverse linear dynamics of the closed loop system, is applied to make the output  follow the desired output
follow the desired output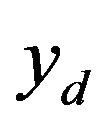 . This control scheme can be seen as being evolved from the open-loop control scheme shown in Figure 7. The rationale behind this scheme is that the accurate modeling and inversion of the nonlinear effects such as hysteresis are complicated whist the inversion of a linear plant is relatively easy to compute [139]. However the low gain margin problem with the feedback loop exists in this scheme [19]. Also, similar to the open-loop control schemes, this scheme is sensitive to the disturbances acting outside the closed-loop system.
. This control scheme can be seen as being evolved from the open-loop control scheme shown in Figure 7. The rationale behind this scheme is that the accurate modeling and inversion of the nonlinear effects such as hysteresis are complicated whist the inversion of a linear plant is relatively easy to compute [139]. However the low gain margin problem with the feedback loop exists in this scheme [19]. Also, similar to the open-loop control schemes, this scheme is sensitive to the disturbances acting outside the closed-loop system.
4.4. Disturbance Observer Based Schemes
Recently, a technique call disturbance observer is used for the compensation of hysteresis and other nonlinear/uncertain effects in PEAs. In this scheme, a PEA is modeled as a linear dynamic system , so when subject to the same input voltage
, so when subject to the same input voltage , the output of the PEA
, the output of the PEA 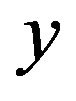 and that of the corresponding
and that of the corresponding 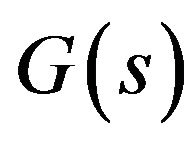 are different due to hysteresis and other nonlinear/uncertain effects. The disturbance observer utilizes
are different due to hysteresis and other nonlinear/uncertain effects. The disturbance observer utilizes 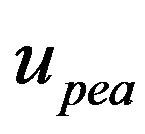 and
and  to estimate an additional input voltage
to estimate an additional input voltage  such that if
such that if 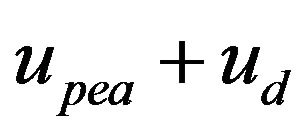 is applied to
is applied to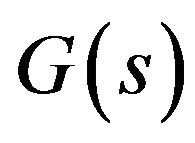 , the output of
, the output of  is the same as
is the same as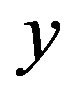 .
.  is referred to as an input distur-
is referred to as an input distur-
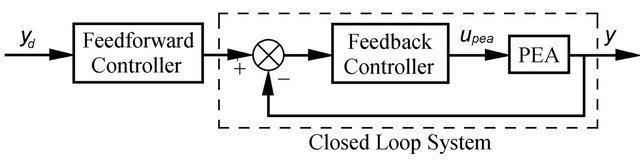
Figure 10. A feedback controller is used for nonlinear suppression whist a feedforward controller is the inverse model of the closed loop system for canceling out the dynamics of the closed loop system, which can be treated as linear [19].
bance to  that represents the hysteresis and other nonlinear/uncertain effects. As such, to compensate for hysteresis and other nonlinear/uncertain effects in the PEA, one only needs to subtract
that represents the hysteresis and other nonlinear/uncertain effects. As such, to compensate for hysteresis and other nonlinear/uncertain effects in the PEA, one only needs to subtract 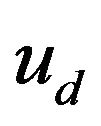 from
from 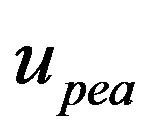 before
before  being applied to the PEA. A control scheme with such a disturbance observer is shown in Figure 11. This scheme has been shown to be effective in both step [140] and high frequency tracking (200 Hz sinusoidal) [141] operations.
being applied to the PEA. A control scheme with such a disturbance observer is shown in Figure 11. This scheme has been shown to be effective in both step [140] and high frequency tracking (200 Hz sinusoidal) [141] operations.
5. Emerging Issues in PEA Modeling and Control
Based on the reviews in the previous sections, some emerging issues regarding the modeling and control of PEAs and PEA-driven positioning stages are discussed in this section.
5.1. Modeling Issues
5.1.1. Limitations of Some Existing Hysteresis Models of PEAs
While the modeling of creep and vibration dynamics of PEAs have been relatively well address, the existing models of hysteresis, especially the rate-independent hysteresis models reviewed in Section 3.1.2, still possess issues, as follows. Though being highly effective in representing both the major hysteresis loops and the minor hysteresis loops, it is noted in the literature [40,53-56,58] that the Preisach hysteresis model cannot at the same time represent the initial ascending curve when the PEA is subject to nonnegative voltage inputs. This is due to the fact that the Preisach hysteresis operator has only two saturation values and without a separate initial section that connects the origin to the hysteresis loop (Figure 2(a)). The PI hysteresis models and the MRC hysteresis model do not suffer from this problem due to the existence of initial sections in their respective hysteresis operator besides the hysteresis loop (Figures 3(a) and 4(a)(2)). However, to limit the computational effort, the number of hysteresis operators used in PI or MRC hysteresis models in practice is usually very small (typically around 10) compared to the Preisach hysteresis model (infinity). As a result, the PI and MRC models tend to be less accurate than the Preisach hysteresis model in representing the hysteresis loops, especially in the cases of the small minor loops. So, given a tractable amount of computational effort, there is a contradiction between the capability of representing all hysteresis phenomena, including one-sided hysteresis (the PI and MRC hysteresis models), and the accuracy (Preisach hysteresis models) in the existing rate-independent hysteresis models. This remains an issue to be solved in future research.
5.1.2. Applications of Different Actuator Structures
The applications of PEA-driven positioning systems with structures different from the conventional ones (those can be treated as a mass fixed to one end of the PEA) also pose modeling problems. A typical example is the PEAdriven stick-slip actuator shown in Figure 12, in which an end-effector is supported and guided by a movable platform that is driven by a PEA, and it works as follows. During the course of slow expansion of the PEA, the end-effector moves along with the platform. If the PEA suddenly contracts, the end-effector slides on the platform because the force due to inertia becomes larger than the friction between the end-effector and the movable platform. As a result, the end-effector moves a step, 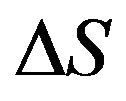 , with respect to its original position. Such steps can be accumulated to achieve a theoretically unlimited displacement (actually limited by the size of the moveable platform). The modeling of the dynamics of the endeffector displacement has not been well addressed in the literature. Chang and Li [142] developed a model for the PEA-driven stick-slip actuator without considering the dynamics of the PEA while the friction involved was modeled as Coulomb friction, which is over simplified. By taking into account presliding friction, models were developed and reported in more recent studies on stickslip actuators, e.g. [143]. However, issues including the
, with respect to its original position. Such steps can be accumulated to achieve a theoretically unlimited displacement (actually limited by the size of the moveable platform). The modeling of the dynamics of the endeffector displacement has not been well addressed in the literature. Chang and Li [142] developed a model for the PEA-driven stick-slip actuator without considering the dynamics of the PEA while the friction involved was modeled as Coulomb friction, which is over simplified. By taking into account presliding friction, models were developed and reported in more recent studies on stickslip actuators, e.g. [143]. However, issues including the
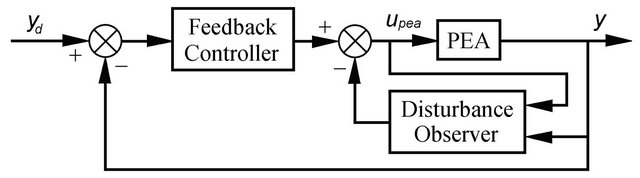
Figure 11. Augmenting the feedback control loop with a disturbance observer.

Figure 12. Actuation sequence of a PEA-driven stick-slip actuator; (a) Start; (b) Slow expansion and (c) Fast contraction.
influence of PEA nonlinearities and the end-effector mass on the performance of the PEA-driven stick-slip actuator remain to be addressed.
5.2. Control Issues
5.2.1. Controller Design
As can be seen from Section 4.2, sliding mode control has been one of the most promising techniques for PEA control applications due to their capability to largely suppress hysteresis and creep in practice. However, there are two remaining problems. One problem of implementing the sliding mode control techniques on PEAs is chattering. This is a kind of high frequency vibration in the plant output displacement induced by the discontinuous control signal generated by a sliding mode controller, and it can induce wear, noises, and even resonance and instability in the plant. Chattering is especially severe in plants with fast responses, such as PEAs, because they cannot filter out the high frequency component in the switching control signal. Another problem is that the bounds of the matched uncertainties need to be known for designing the discontinuous control signal, but such bounds are usually difficult to determine in practice while conservatively setting the bounds to large values only leads to more severe chattering [110]. Existing research efforts have been focused on solving the chattering problem. For example, a method referred to as the sliding mode with boundary layer control was developed by approximating the discontinuous control signal with a continuous one, but with the cost of introducing nonzero steady state error, and chattering is still significant if the bounds of the matched uncertainties are large [110]. Higher order sliding surfaces are also used for chattering suppression, such as the integral sliding mode technique in [92,144] and the PID sliding surface in [115]. However, the second problem remains to be solved.
5.2.2. State Estimation
Many advanced control techniques reviewed in Section 4, such as sliding mode control [114], require state feedback. Since usually not all of the states of a PEA model are measurable in application, state observers must be used. However, the problem of estimating the states of PEA models has not been well addressed in the literature, as discussed below.
Currently, many kinds of state observers are applicable to PEA control and they can be classified into two categories: non-model-based and model-based. Non-modelbased filters/differentiators, such as the low-pass filter plus ideal differentiator, the α-β filter [145], the highgain differentiator [146], the integral-chain differentiator [146], and the sliding mode differentiator based on the super-twisting algorithm [147] (given that the states needed are the derivatives of the measured plant output), usually generate large phase lags if the desired level of noise suppression is enforced (for the first four aforementioned methods) or excessive chattering in noisy systems (for the last method). Compared to non-modelbased filters/differentiators, model-based observers, e.g., the extended Kalman filter [148], the unscented Kalman filter [149,150], and the high-gain observer [114], can generate more accurate estimations if the imperfection of the model can be ignored. However, with the presence of uncertainties such as the effects of hysteresis, creep, and external load on a PEA, however, the performances of the model-based observers degrade. For improvement, in the cases that the system uncertainties can be treated as a lumped unknown input to the system model, a kind of model-based observers should be used to estimate the system states even with the presence of the unknown input, which is referred to as unknown input observers (UIOs) in the literature. Many UIOs have been reported in the past three decades, including the full-order UIO [151], the reduced-order UIO [152], the UIO designed based on projection operator [153], and the slidingmode-based observers (SMOs) [110,153-155].
Applications of these UIOs require that the observer matching condition be satisfied [156,157], which states that the rank of the product of the output matrix and the unknown input matrix in the state space model of the system must be equal to that of the unknown input matrix [110]. However, existing PEA models, such as the one in [92], do not meet this condition. Attempts to relax the observer matching condition have been reported [156,157], but the resultant UIOs were very complicated. As such, a UIO with a simpler structure and the capability of relaxing the observer matching condition still needs to be developed in future research for the use in PEA tracking control.
5.3. Modeling and Control of Multi-Degree-of-Freedom (Multi-DOF) PEA-Driven Positioning Systems
All of the above discussions have been focused on single-DOF PEA-driven positioning systems. However, there are modeling and control issues uniquely related to multi-DOF PEA-driven positioning systems and they are briefly discussed in this section.
The multi-DOF PEA-driven positioning systems reported in the literature can be divided in to two categories: series mechanisms and parallel mechanisms. Among which, multi-DOF PEA-driven series mechanisms [16] and the xyz-type parallel mechanisms (translations along x-, yand z-axis) such as those in [16,158-160] can usually be treated as a series of individual 1-DOF PEAdriven mechanisms without significant coupling between the moving axes, as such their modeling and control can be well address with the techniques applied to the single-DOF systems.
The remaining multi-DOF PEA-driven parallel mechanisms whose moving axes are significantly coupled can be further divided into fully-actuated systems, i.e. the number of actuation is the same as the number of DOF [17,114,161-167], and over-actuated systems, i.e. the number of actuation is the more than the number of DOF [20,112].
For the fully-actuated systems, their models are usually established based on the geometric structure of the mechanism and mechanics. Since most of such mechanisms use flexure hinges instead of conventional hinges to avoid friction and backlash [17,114,158,159-166], the modeling of the flexure hinges becomes an important part in modeling such mechanisms [114,160,166]. Two kinds of workflows can be adopted for modeling the multi-DOF PEA-driven positioning systems. For the first kind of workflows, a kinematic model is firstly constructed based on the geometric structure of the mechanism, and then either a phenomenological [114] or physical [160] dynamic model can be established based on the kinematic model. The second kind of workflows involves direct identification of the dynamic model of the mechanism without establishing the kinematic model [16].
Many control schemes that have been applied to control single-DOF PEA-driven positioning systems can also be extended to control fully-actuated PEA-driven positioning systems, e.g. PID control [112,168], H2 control [168], and sliding mode control [112] since such methods can be easily extended to fully-actuated multi-inputmulti-output cases.
Compared to the fully-actuated systems, the overactuated systems have certain advantages in the performance point of view, e.g. singularity elimination, dexterity improvement, and better load carrying ability [169]. However, the over-actuated structure poses difficulties in both modeling and control. Specifically, the PEAs in the mechanism need to cooperate well or excessive internal forces will occur and may damage the mechanism, whilst the involvement of PEA nonlinearities makes such cooperation difficult to model and control. As a result, very few researches on the modeling and control of over-actuated PEA-driven parallel mechanism have been reported compared to its popularity in macro parallel mechanisms. The only example is [112], in which the modeling and control of a xθyθz 3-DOF positioning system driven by 4 PEAs are concerned. Specifically, in [112] each PEA in the mechanism is modeled and controlled individually and uses only the output displacements of the corresponding PEA as feedback, while the inverse kinematic model of the mechanism is used to generate the desired displacement for each PEA according to the desired position of the end-effector. The cross-axis couplings are considered as disturbances. As such, the control problem is transformed into several 1-DOF control problems, which are much simpler. However, in this scheme the actual position of the end-effector is not closed-loopcontrolled, and the requirement of being able to measure the displacement of each PEA in the mechanism limits the generality of this scheme. As such, more general schemes for modeling and controlling over-actuated multiDOF PEA-driven positioning systems that can relax the aforementioned requirement are still to be developed in the future.
6. Conclusions
Though possessing fine resolution, high actuating forces, and fast responses, the nonlinear effects make modeling and control of PEAs for the use in microand nanopositioning challenging. Researches for solving such problems are abundant, and the resulting typical methods developed are reviewed in this paper, from which some major conclusions can be drawn: 1) the decoupledstructure PEA models have the advantages of being more accurate and flexible as compared to the undecoupled ones; 2) in the decoupled-structure PEA models, the submodels concerning vibration dynamics and creep have been relatively well addressed in the literature; 3) however, among the existing hysteresis sub-models, for a tractable among of computation efforts, a contradiction between the capability of representing all hysteresis phenomena and maintaining model accuracy remains to be solved; 4) among the control schemes reviewed, the sliding mode control is among the most promising ones as applied to PEA positioning since when designed based on the decoupled-structure PEA models, it can completely reject the hysteresis and creep effects in theory; 5) however, there are still issues associated with sliding mode control (chattering) and the corresponding state estimators (the incompatibility between the observer matching condition and the existing PEA models); finally, 6) the modeling and control of some PEA-driven positioning systems with unconventional structures, e.g. PEA-driven stick-slip actuators and over-actuated multiDOF PEA-driven positioning systems, are largely untouched in the literature, thus remain to be addressed in future research.
REFERENCES
- D. Croft, G. Shed and S. Devasia, “Creep, Hysteresis, and Vibration Compensation for Piezoactuators: Atomic Force Microscopy Application,” Journal of Dynamic Systems, Measurement, and Control, Vol. 123, No. 1, 2001, pp. 35-43. doi:10.1115/1.1341197
- Q. Zou, K. K. Leang, E. Sadoun, M. J. Reed and S. Devasia, “Control Issues in High-Speed AFM for Biological Applications: Collagen Imaging Example,” Asian Journal of Control, Vol. 6, No. 2, 2004, pp. 164-178. doi:10.1111/j.1934-6093.2004.tb00195.x
- R. Kassies, K. O. Van der Werf, A. Lenferink, C. N. Hunter, J. D. Olsen, V. Subramaniam and C. Otto, “Combined AFM and Confocal Fluorescence Microscope for Applications in Bio-Nanotechnology,” Journal of Microscopy, Vol. 217, No. 1, 2005, pp. 109-116. doi:10.1111/j.0022-2720.2005.01428.x
- H. Song, G. Vdovin, R. Fraanje, G. Schitter and M. Verhaegen, “Extracting Hysteresis from Nonlinear Measurement of Wavefront-Sensorless Adaptive Optics System,” Optics Letters, Vol. 34, No. 1, 2009, pp. 61-63. doi:10.1364/OL.34.000061
- W. Yang, S.-Y. Lee and B.-J. You, “A Piezoelectric Actuator with a Motion-Decoupling Amplifier for Optical Disk Drives,” Smart Materials and Structures, Vol. 19, No. 6, 2010, pp. 065027.1-065027.10. doi:10.1088/0964-1726/19/6/065027
- G. Stöppler and S. Douglas, “Adaptronic Gantry Machine Tool with Piezoelectric Actuator for Active Error Compensation of Structural Oscillations at the Tool Centre Point,” Mechatronics, Vol. 18, No. 8, 2008, pp. 426-433. doi:10.1016/j.mechatronics.2008.03.002
- S. R. Viswamurthy, A. K. Rao and R. Ganguli, “Dynamic Hysteresis of Piezoceramic Stack Actuators Used in Helicopter Vibration Control: Experiments and Simulations,” Smart Materials and Structures, Vol. 16, No. 4, 2007, pp. 1109-1119. doi:10.1088/0964-1726/16/4/020
- M. S. Senousy, F. X. Li, D. Mumford, M. Gadala and R. K. N. D. Rajapakse, “Thermo-Electro-Mechanical Performance of Piezoelectric Stack Actuators for Fuel Injector Applications,” Journal of Intelligent Material Systems and Structures, Vol. 20, No. 4, 2009, pp. 387-399. doi:10.1177/1045389X08095030
- J.-J. Wei, Z.-C. Qiu, J.-D. Han and Y.-C. Wang, “Experimental Comparison Research on Active Vibration Control for Flexible Piezoelectric Manipulator Using Fuzzy Controller,” Journal of Intelligent and Robotic Systems, Vol. 59, No. 1, 2010, pp. 31-56. doi:10.1007/s10846-009-9390-2
- D. Shu, J. Maser, M. Holt, R. Winarski, C. Preissner, A. Smolyanitskiy, B. Lai, S. Vogt and G. B. Stephenson, “Optomechanical Design of a Hard X-Ray Nanoprobe Instrument with Nanometer-Scale Active Vibration Control,” AIP Conference Proceedings, Vol. 879, 2007, pp. 1321-1324. doi.org/10.1063/1.2436307
- H. Zhou and B. Henson, “Analysis of a Diamond-Shaped Mechanical Amplifier for a Piezo Actuator,” The International Journal of Advanced Manufacturing Technology, Vol. 32, No. 1-2, 2007, pp. 1-7. doi:10.1007/s00170-005-0303-7
- M. Muraokaa and S. Sanada, “Displacement Amplifier for Piezoelectric Actuator Based on Honeycomb Link Mechanism,” Sensors and Actuators A: Physical, Vol. 157, No. 1, 2010, pp. 84-90. doi:10.1016/j.sna.2009.10.024
- Y. Zhang, G. Liu and J. Hesselbach, “On Development of a Rotary-Linear Actuator Using Piezoelectric Translators,” IEEE/ASME Transactions on Mechatronics, Vol. 11, No. 5, 2006, pp. 647-650. doi:10.1109/TMECH.2006.882998
- J. Li, R. Sedaghati, J. Dargahi and D. Waechter, “Design and Development of a New Piezoelectric Linear Inchworm Actuator,” Mechatronics, Vol. 15, No. 6, 2005, pp. 651-681. doi:10.1016/j.mechatronics.2005.02.002
- R. Merry, R. Van de Molengraft and M. Steinbuch, “Modeling of a Walking Piezo Actuator,” Sensors and Actuators A: Physical, Vol. 162, No. 1, 2010, pp. 51-60. doi:10.1016/j.sna.2010.05.033
- R. Merry, M. Uyanik, R. Van de Molengraft, R. Koops, M. Van Veghel and M. Steinbuch, “Identification, Control and Hysteresis Compensation of a 3 DOF Metrological AFM,” Asian Journal of Control, Vol. 11, No. 2, 2009, pp. 130-143. doi:10.1002/asjc.89
- T.-F. Lu, D. C. Handley, Y. K. Yong and C. Eales, “A Three-DOF Compliant Micromotion Stage with Flexure Hinges,” Industrial Robot: An International Journal, Vol. 31, No. 4, 2004, pp. 355-361. doi:10.1108/01439910410541873
- S. W. Lee, K.-G. Ahn and J. Ni, “Development of a Piezoelectric Multi-Axis Stage Based on Stick-and-Clamping Actuation Technology,” Smart Materials and Structures, Vol. 16, No. 6, 2007, pp. 2354-2367. doi:10.1088/0964-1726/16/6/040
- S. Devasia, E. Eleftheriou and S. O. R. Moheimani, “A Survey of Control Issues in Nanopositioning,” IEEE Transactions on Control Systems Technology, Vol. 15, No. 5, 2007. pp. 802-823. doi:10.1109/TCST.2007.903345
- P. Instrumente, “The World of Nanopositioning and Micropositioning 2005/2006,” Physik Instrumente, Karlsruhe, 2005.
- I. Mayergoyz and G.Bertotti (Eds.), “The Science of Hysteresis,” Vol. 3, Elsevier, St. Louis, 2005.
- H. J. M. T. S. Adriaens, W. L. De Koning and R. Banning, “Modeling Piezoelectric Actuators,” IEEE/ASME Transactions on Mechatronics, Vol. 5, No. 4, 2000, pp. 331- 341. doi:10.1109/3516.891044
- J. A. Main and E. Garcia, “Piezoelectric Stack Actuators and Control System Design: Strategies and Pitfalls,” Journal of Guidance, Control, and Dynamics, Vol. 20, No. 3, 1997, pp. 479-485. doi:10.2514/2.4066
- T. Fett and G. Thun, “Determination of Room-Temperature Tensile Creep of PZT,” Journal of Materials Science Letters, Vol. 17, No. 22, 1998, pp. 1929-1931. doi:10.1023/A:1006608509876
- W. T. Ang, F. A. Garmón, P. Khosla and C. N. Riviere, “Modeling Rate-Dependent Hysteresis in Piezoelectric Actuator,” 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, 27 October-1 November 2003, pp. 1975-1980. doi:10.1109/IROS.2003.1248937
- W. T. Ang, P. K. Khosla and C. N. Riviere, “Feedforward Controller with Inverse Rate-Dependent Model for Piezoelectric Actuators in Trajectory-Tracking Applications,” IEEE/ASME Transactions on Mechatronics, Vol. 12, No. 2, 2007, pp. 134-142. doi:10.1109/TMECH.2007.892824
- R. S. Robinson, “Interactive Computer Correction of Piezoelectric Creep in Scanning Tunneling Microscopy Images,” Journal of Computer-Assisted Microscopy, Vol. 2, No. 1, 1996, pp. 53-58.
- X. B. Chen, Q. Zhang, D. Kang and W. Zhang, “On the Dynamics of Piezoactuated Positioning Systems,” Review of Scientific Instruments, Vol. 79, No. 11, 2008, pp. 116101.1-116101.3. doi:10.1063/1.2982238
- W. Chen and C. S. Lynch, “A Micro-Electro-Mechanical Model for Polarization Switching of Ferroelectric Materials,” Acta Materialia, Vol. 46, No. 15, 1998, pp. 5305- 5311. doi:10.1016/S1359-6454(98)00207-9
- W. Seemann, A. Arockiarajan and B. Delibas, “Modeling and Simulation of Piezoceramic Materials Using Micromechanical Approach,” European Congress on Computaional Methods in Applied Sciences and Engineering 2004 (ECCOMAS 2004), Jyväskylä, 24-28 July 2004.
- A. Arockiarajan, B. Delibas, A. Menzel and W. Seemann, “Studies on Nonlinear Electromechanical Behavior of Piezoelectric Materials Using Finite Element Modeling,” IWPMA 2005, 2nd International Workshop on Piezoelectric Materials and Applications in Actuators, Heinz Nixdorf Institute, Paderborn, 22-25 May 2005.
- B. Delibas, A. Arockiarajan and W. Seemann, “Intergranular Effects on Domain Switchings in Polycrystalline Piezoceramics,” IWPMA 2005, 2nd International Workshop on Piezoelectric Materials and Applications in Actuators, Heinz Nixdorf Institute, Paderborn, 22-25 May 2005.
- M. Kamlah and Q. Jiang, “A Constitutive Model for Ferroelectric PZT Ceramics under Uniaxial Loading,” Smart Materials and Structures, Vol. 8, No. 4, 1999, pp. 441- 459. doi:10.1088/0964-1726/8/4/302
- M. Kamlah and C. Tsakmakis, “Phenomenological Modeling of the Non-Linear Electro-Mechanical Coupling in Ferroelectrics,” International Journal of Solids and Structures, Vol. 36, No. 5, 1999, pp. 669-695. doi:10.1016/S0020-7683(98)00040-7
- M. Kamlah and U. Böhle, “Finite Element Analysis of Piezoceramic Components Taking into Account Ferroelectric Hysteresis Behavior,” International Journal of Solids and Structures, Vol. 38, No. 4, 2001, pp. 605-633. doi:10.1016/S0020-7683(00)00055-X
- C. M. Landis, J. Wang and J. Sheng, “Microelectromechanical Determination of the Possible Remanent Strain and Polarization States in Polycrystalline Ferroelectrics and the Implications for Phenomenological Constitutive Theories,” Journal of Intelligent Material Systems and Structures, Vol. 15, No. 7, 2004, pp. 513-525. doi:10.1177/1045389X04041653
- J. Schröder and H. Romanowski, “A Simple Coordinate Invariant Thermodynamic Consistent Model for Nonlinear Electro-Mechanical Coupled Ferroelectrica,” European Congress on Computaional Methods in Applied Sciences and Engineering 2004 (ECCOMAS 2004), Jyvä- skylä, 24-28 July 2004.
- J. Schröder and H. Romanowski, “A Thermodynamically Consistent Mesoscopic Model for Transversely Isotropic Ferroelectric Ceramics in a Coordinate-Invariant Setting,” Achive of Applied Mechanics, Vol. 74, No. 11-12, 2005, pp. 863-877. doi:10.1007/s00419-005-0412-7
- S. Klinkel, “A Thermodynamic Consistent 1D Model for Ferroelastic and Ferroelectric Hysteresis Effects in Piezoceramics,” Communications in Numerical Methods in Engineering, Vol. 22, No. 7, 2006, pp. 727-739. doi:10.1002/cnm.845
- T. Hegewald, B. Kaltenbacher, M. Kaltenbacher and R. Lerch, “Efficient Modeling of Ferroelectric Behavior for the Analysis of Piezoceramic Actuators,” Journal of Intelligent Material Systems and Structures, Vol. 19, No. 10, 2008, pp. 1117-1129. doi:10.1177/1045389X07083608
- IEEE, “ANSI/ IEEE Std. 176-1987: IEEE Standard on Piezoelectricity,” The Institute of Electrical and Electronics Engineers, New York, 1988.
- P. G. Harper, “Kinematic Theory of Piezoelectric Hysteresis,” Journal of Applied Physics, Vol. 52, No. 11, 1981, pp. 6851-6855. doi:10.1063/1.328677
- D. C. Jiles and D. L. Atherton, “Theory of the Magnetisation Process in Ferromagnets and Its Application to the Magnetomechanical Effect,” Journal of Physics D: Applied Physics, Vol. 17, No. 6, 1984, pp. 1265-1281. doi:10.1088/0022-3727/17/6/023
- R. C. Smith and C. L. Hom, “Domain Wall Model for Ferroelectric Hysteresis,” Technical Report CRSC-TR99- 07, Center for Research in Scientific Computation, New York, 1999.
- T. Hegewald, M. Kaltenbacher and R. Lerch, “Characterization and Modeling of Piezoelectric Stack Actuators,” IWPMA 2005, 2nd International Workshop on Piezoelectric Materials and Applications in Actuators, Heinz Nixdorf Institute, Paderborn, 22-25 May 2005, pp. 99- 106.
- E. Preisach, “On the Magnetic Aftereffect,” Zeitschrift für Physik A Hadrons and Nuclei, Vol. 94, No. 5-6, 1935, pp. 277-302.
- I. D. Mayergoyz, “Mathematical Models of Hysteresis,” Physical Review Letters, Vol. 56, No. 15, 1986, pp. 1518- 1521. doi:10.1103/PhysRevLett.56.1518
- I. D. Mayergoyz and G. Friedman, “Generalized Preisach model of Hysteresis,” IEEE Transactions on Magnetics, Vol. 24, No. 1, 1988, pp. 212-217. doi:10.1109/20.43892
- P. Hejda and T. Zelinka, “Generalized Preisach Model of Hysteresis—Theory and Experiment,” Czechoslovak Journal of Physics, Vol. 40, No. 1, 1990, pp. 57-68. doi:10.1007/BF01598355
- M.-J. Jang, C.-L. Chen and J.-R. Lee, “Modeling and Control of a Piezoelectric Actuator Driven System with Asymmetric Hysteresis,” Journal of the Franklin Institute, Vol. 346, No. 1, 2009, pp. 17-32. doi:10.1016/j.jfranklin.2008.06.005
- P. N. Sreeram, G. Salvady and N. G. Naganathan, “Hysteresis Prediction for a Piezoceramic Material System,” The ASME Winter Annual Meeting, New Orleans, 28 November-3 December 3 1993, pp. 35-42.
- D. C. Hughes and J. T. Wen, “Preisach Modeling and Compensation for Smart Material Hysteresis,” Proceedings of SPIE, Vol. 2427, 1995, pp. 50-64.
- P. Ge and M. Jouaneh, “Generalized Preisach Model for Hysteresis Nonlinearity of Piezoceramic Actuators,” Precision Engineering, Vol. 20, No. 2, 1997, pp. 99-111. do:10.1016/S0141-6359(97)00014-7
- H. Hu and R. B. Mrad, “On the Classical Preisach Model for Hysteresis in Piezoceramic Actuators,” Mechatronics, Vol. 13, No. 2, 2002, pp. 85-94. doi:10.1016/S0957-4158(01)00043-5
- G. Robert, D. Damjanovic and N. Setter, “Preisach Modeling of Piezoelectric Nonlinearity in Ferroelectric Ceramics,” Journal of Applied Physics, Vol. 89, No. 9, 2001, pp. 5067-5074. doi:10.1063/1.1359166
- G. Song, J. Zhao, X. Zhou and J. A. De Abreu-Garcia, “Tracking Control of a Piezoceramic Actuator with Hysteresis Compensation Using Inverse Preisach Model,” IEEE/ASME Transactions on Mechatronics, Vol. 10, No. 2, 2005, pp. 198-209. doi:10.1109/TMECH.2005.844708
- X. Zhao and Y. Tan, “Neural Network based Identification of Preisach-Type Hysteresis in Piezoelectric Actuator Using Hysteretic Operator,” Sensors and Actuators A: Physical, Vol. 126, No. 2, 2006, pp. 306-311. doi:10.1016/j.sna.2005.10.023
- X. Zhao and Y. Tan, “Modeling Hysteresis in Piezo Actuator based on Neural Networks,” Advances in Computation and Intelligence, Lecture Notes in Computer Science, Vol. 5370, 2008, pp. 290-296.
- K. Kuhnen and H. Janocha, “Adaptive Inverse Control of Piezoelectric Actuators with Hysteresis Operators,” Proceedings of European Control Conference (ECC), Karsruhe, 31 August-3 September 1999, paper F 0291.
- [61] P. Krejci and K. Kuhnen, “Inverse Control of Systems with Hysteresis and Creep,” IEE Proceedings—Control Theory and Applications, Vol. 148, No. 3, 2001, pp. 185- 192. doi:10.1049/ip-cta:20010375
- [62] K. Kuhnen and H. Janocha, “Complex Hysteresis Modeling of a Broad Class of Hysteretic Nonlinearities,” Proceedings of the 8th international conference on New Actuators, Bremen, 10-12 June 2002, pp. 688-691.
- [63] K. Kuhnen and F. Previdi, “Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities: A Modified Prandtl-Ishlinskii Spproach,” European Journal of Control, Vol. 9, No. 4, 2003, pp. 407-421. doi:10.3166/ejc.9.407-418
- [64] K. Kuhnen, “Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities and Log(t)-Type Creep Dynamics,” Control and Intelligent System, Vol. 33, No. 2, 2005, pp. 134-147. doi:10.2316/Journal.201.2005.2.201-1420
- [65] M. Goldfarb and N. Celanovic, “Modeling Piezoelectric Stack Actuators for Control of Micromanipulation,” IEEE Control Systems Magazine, Vol. 17, No. 3, 1997, pp. 69- 79. doi:10.1109/37.588158
- [66] S.-H. Lee, T. J. Royston and G. Friedman, “Modeling and Compensation of Hysteresis in Piezoceramic Transducers for Vibration Control,” Journal of Intelligent Material Systems and Structures, Vol. 11, No. 10, 2000, pp. 781- 790. doi:10.1106/GQLJ-JGEU-MHG1-7JDF
- [67] T.-J. Yeh, S.-W. Lu and T.-Y. Wu, “Modeling and Identification of Hysteresis in Piezoelectric Actuators,” Journal of Dynamic Systems, Measurement, and Control, Vol. 128, No. 2, 2006, pp. 189-196. doi:10.1115/1.2192819
- [68] T.-J. Yeh, R.-F. Hung and S.-W. Lu, “An Integrated Physical Model that Characterizes Creep and Hysteresis in Piezoelectric Actuators,” Simulation Modelling Practice and Theory, Vol. 16, No. 1, 2008, pp. 93-110. doi:10.1016/j.simpat.2007.11.005
- [69] R. B. Mrad and H. Hu, “A Model for Voltage to Displacement Dynamics in Piezoceramic Actuators Subject to Dynamic Voltage Excitations,” IEEE/ASME Transactions on Mechatronics, Vol. 7, No. 4, 2002, pp. 479-489. doi:10.1109/TMECH.2002.802724
- [70] D. Song and C. J. Li, “Modeling of Piezo Actuator’s Nonlinear and Frequency Dependent Dynamics,” Mechatronics, Vol. 9, No. 4, 1999, pp. 391-410. doi:10.1016/S0957-4158(99)00005-7
- [71] Y. Yu, Z. Xiaob, N. G. Naganathan and R. V. Dukkipati, “Dynamic Preisach Modeling of Hysteresis for the Piezoceramic Actuator System,” Mechanism and Machine Theory, Vol. 37, No. 1, 2002, pp. 75-89. doi:10.1016/S0094-114X(01)00065-9
- [72] X. Tan, R. Venkataraman and P. S. Krishnaprasad, “Control of Hysteresis: Theory and Experimental Results,” Pentagon Technical Report A687934, 2001.
- [73] H. Hu and R. Ben Mrad, “A Discrete-Time Compensation Algorithm for Hysteresis in Piezoceramic Actuators,” Mechanical Systems and Signal Processing, Vol. 18, No. 1, 2004, pp. 169-185. doi:10.1016/S0888-3270(03)00021-9
- [74] S. Bashash and N. Jalili, “A Polynomial-Based Linear Mapping Strategy for Feedforward Compensation of Hysteresis in Piezoelectric Actuators,” Journal of Dynamic Systems, Measurement, and Control, Vol. 130, No. 3, 2008, pp. 031008.1-031008.10. doi:10.1115/1.2907372
- [75] R. Venkataraman and P. S. Krishnaprasad, “Novel Algorithm for the Inversion of the Preisach Operator Smart Structures and Materials,” Proceedings of SPIE 3984, Smart Structures and Materials 2000: Mathematics and Control in Smart Structures, 2000, pp. 404-414. doi:10.1117/12.388785
- [76] R. Venkataraman and P. S. Krishnaprasad, “Approximate Inversion of Hysteresis: Theory and Numerical Results,” Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12-15 December 2000, pp. 4448-4454. doi:10.1109/CDC.2001.914608
- [77] J. Y. Peng and X. B. Chen, “H2-Optimal Digital Control of Piezoelectric Actuators,” Proceedings of the 8th World Congress on Intelligent Control and Automation, WCICA- 2010, Jinan, 7-9 July 2010, pp. 3684-3690. doi:10.1109/WCICA.2010.5553921
- [78] U.-X. Tan, W. T. Latt, C. Y. Shee, C. N. Riviere and W. T. Ang, “Feedforward Controller of Ill-Conditioned Hysteresis Using Singularity-Free Prandtl-Ishlinskii Model,” IEEE/ASME Transactions on Mechatronics, Vol. 14, No. 5, 2009, pp. 598-605. doi:10.1109/TMECH.2008.2009936
- [79] B. D. Coleman and M. L. Hodgdon, “A Constitutive Relation for Rate-Independent Hysteresis in Ferromagnetically Soft Materials,” International Journal of Engineering Science, Vol. 24, No. 6, 1986, pp. 897-919. doi:10.1016/0020-7225(86)90023-6
- [80] R. Bouc, “Forced Vibrations of a Mechanical System with Hysteresis,” Proceedings of the 4th Conference on Non-linear Oscillations, Prague, 5-9 September 1967, pp. 315.
- [81] Y.-K. Wen, “Method of Random Vibration of Hysteretic Systems,” Journal of the Engineering Mechanics Division, Vol. 102, No. 2, 1976, pp. 249-263.
- [82] M. Ismail, F. Ikhouane and J. Rodellar, “The Hysteresis Bouc-Wen Model, a Survey,” Archives of Computational Methods in Engineering, Vol. 16, No. 2, 2009, pp. 161- 188. doi:10.1007/s11831-009-9031-8
- [83] O. Gomis-Bellmunt, F. Ikhouane and D. MontesinosMiracle, “Control of Bouc-Wen Hysteretic Dystems: Application to a Piezoelectric Actuator,” The 13th Power Electronics and Motion Control Conference, 2008. EPEPEMC 2008, Poznan, 1-3 September 2008, pp. 1670- 1675. doi:10.1109/EPEPEMC.2008.4635507
- [84] M. Rakotondrabe, “Bouc-Wen Modeling and Inverse Multiplicative Structure to Compensate Hysteresis Nonlinearity in Piezoelectric Actuators,” IEEE Transactions on Automation Science and Engineering, Vol. 8, No. 2, 2011, pp. 428-431. doi:0.1109/TASE.2010.2081979
- [85] D. H. Wang, W. Zhu and Q. Yang, “Linearization of Stack Piezoelectric Ceramic Actuators Based on BoucWen Model,” Journal of Intelligent Material Systems and Structures, Vol. 22, No. 5, 2011, pp. 401-413. doi:10.1177/1045389X10386132
- [86] L. Deng and Y. Tan, “Modeling Hysteresis in Piezoelectric Actuators Using NARMAX Models,” Sensors and Actuators A: Physical, Vol. 149, No. 1, 2009, pp. 106- 112. doi:10.1016/j.sna.2008.09.022
- [87] A. Badel, J. Qiu and T. Nakano, “A New Simple Asymmetric Hysteresis Operator and Its Application to Inverse Control of Piezoelectric Actuators,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 55, No. 5, 2008, pp. 1086-1094. doi:10.1109/TUFFC.2008.761
- [88] H. Jung, J. Y. Shim and D. Gweon, “New Open-Loop Actuating Method of Piezoelectric Actuators for Removing Hysteresis and Creep,” Review of Scientific Instruments, Vol. 71, No. 9, 2000, pp. 3436-3440. doi:10.1063/1.1287627
- [89] K. Kuhnen and H. Janocha, “Compensation of Creep and Hysteresis Effects of Piezoelectric Actuators with Inverse Systems,” 6th International Conference on New Actuators, Actuator’98, Bremen, 17-19 June 1998, pp. 309-312.
- [90] H. Janocha and K. Kuhnen, “Real-Time Compensation of Hysteresis and Creep in Piezoelectric Actuators,” Sensors Actuators A: Physical, Vol. 79, No. 2, 2000, pp. 83-89. doi:10.1016/S0924-4247(99)00215-0
- [91] J. S. Dewey, K. Leang and S. Devasia, “Experimental and Theoretical Results in Output-Trajectory Redesign for Flexible Structures,” Journal of Dynamic Systems, Measurement, and Control, Vol. 120, No. 4, 1998, pp. 456-461. doi:10.1115/1.2801486
- [92] K. S. Abidi and A. Şabanoviç, “Sliding Mode Control for High-Precision Motion of a Piezostage,” IEEE Transactions on Industrial Electronics, Vol. 54, No. 1, 2007, pp. 629-637. doi:10.1109/TIE.2006.885477
- [93] H. C. Liaw, B. Shirinzadeh and J. Smith, “Enhanced Sliding Mode Motion Tracking Control of Piezoelectric Actuators,” Sensors and Actuators A: Physical, Vol. 138, No. 1, 2007, pp. 194-202. doi:10.1016/j.sna.2007.04.062
- [94] G. M. Clayton, S. Tien, A. J. Fleming, S. O. R. Moheimani and S. Devasia, “Inverse-Feedforward of ChargeControlled Piezopositioners,” Mechatronics, Vol. 18, No. 5-6, 2008, pp. 273-281. doi:10.1016/j.mechatronics.2007.07.006
- [95] J. W. Li, X. B. Chen and W. J. Zhang, “A New Approach to Modeling System Dynamics—In the Case of a Piezoelectric Actuator with a Host System,” IEEE/ASME Transactions on Mechatronics, Vol. 15, No. 3, 2010, pp. 371- 380. doi:10.1109/TMECH.2009.2026473
- [96] J. W. Li, X. B. Chen and W. J. Zhang, “Axiomatic-Design-Theory-Based Approach to Modeling Linear High Order System Dynamics,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 2, 2011, pp. 341-350. doi:10.1109/TMECH.2010.2043535
- [97] K. Kuhnen, H. Janocha, D. Thull and A. Kugi, “A New Drive Concept for High-Speed Positioning of Piezoelectric Actuators,” Proceedings of the 10th International Conference on New Actuators, Bremen, 14-16 June 2006, pp. 82-85.
- [98] K. K. Leang and S. Devasia, “Feedback-Linearized Inverse Feedforward for Creep, Hysteresis, and Vibration Compensation in AFM Piezoactuators,” IEEE Transactions on Control Systems Technology, Vol. 15, No. 5, 2007, pp. 927-935. doi:10.1109/TCST.2007.902956
- [99] X. Dang and Y. Tan, “An Inner Product-Based Dynamic Neural Network Hysteresis Model for Piezoceramic Actuators,” Sensors and Actuators A: Physical, Vol. 121, No. 2, 2005, pp. 535-542. doi:10.1016/j.sna.2005.04.003
- [100] C. Ru, L. Chen, B. Shao, W. Rong and L. Sun, “A Hysteresis Compensation Method of Piezoelectric Actuator: Model, Identification and Control,” Control Engineering Practice, Vol. 17, No. 9, 2009, pp. 1107-1114. doi:10.1016/j.conengprac.2009.04.013
- [101] L. Sun, C. Ru, W. Rong, L. Chen and M. Kong, “Tracking Control of Piezoelectric Actuator Based on a New Mathematical Model,” Journal of Micromechanics and Microengineering, Vol. 14, No. 11, 2004, pp. 1439-1444. doi:10.1088/0960-1317/14/11/001
- [102] C. Ru and L. Sun, “Hysteresis and Creep Compensation for Piezoelectric Actuator in Open-Loop Operation,” Sensors and Actuators A: Physical, Vol. 122, No. 1, 2005, pp. 124-130. doi:10.1016/j.sna.2005.03.056
- [103] H. H. Najafabadi, S. M. Rezaei, S. S. Ghidary, M. Zareinejad, K. Razi and R. Seifabadi, “Hysteresis Compensation of Piezoelectric Actuators under Dynamic Load Condition,” IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007. IROS 2007, San Diego, 29 October-2 November 2007, pp. 1166-1171. doi:10.1109/IROS.2007.4399048
- [104] E. Kouno, “A Fast Response Piezoelectric Actuator for Servo Correction of Systematic Errors in Precision Machining,” CIRP Annals-Manufacturing Technology, Vol. 33, No. 1, 1982, pp. 369-372. doi: 10.1016/S0007-8506(07)61444-9
- [105] J. F. Cuttino, A. C. Miller and D. E. Schinstock, “Performance Optimization of a Fast Tool Servo for Single-Point Diamond Turning Machines,” IEEE/ASME Transactions on Mechatronics, Vol. 4, No. 2, 1999, pp. 169-179. doi:10.1109/3516.769543
- [106] J. Lin, H. Chiang and C. C. Lin, “Tuning PID Control Gains for Micro Piezo-Stage in using Grey Relational Analysis,” 2008 International Conference on Machine Learning and Cybernetics, Kunming, 12-15 July 2008, pp. 3863-3868. doi: 10.1109/ICMLC.2008.4621078
- [107] H.-J. Shieh, Y.-J. Chiu and Y.-T. Chen, “Optimal PID Control System of a Piezoelectric Microospitioner,” 2008 IEEE/SICE International Symposium on System Integration, Nagoya, 4 December 2008, pp. 1-5. doi:10.1109/SI.2008.4770417
- [108] D. Y. Abramovitch, S. Hoen and R. Workman, “SemiAutomatic Tuning of PID Gains for Atomic Force Microscopes,” Asian Journal of Control, Vol. 11, No. 2, 2009, pp. 188-195. doi:10.1002/asjc.95
- [109] K. K. Tan, T. H. Lee and H. X. Zhou, “Micro-Positioning of Linear-Piezoelectric Motors Based on a Learning Nonlinear PID Controller,” IEEE/ASME Transactions on Mechatronics, Vol. 6, No. 4, 2001, pp. 428-436. doi:10.1109/3516.974856
- [110] W. S. Oates and R. C. Smith, “Nonlinear Control Design for a Piezoelectric-Driven Nanopositioning Stage,” Pentagon Technical Report A591444, 2005.
- [111] C. Edwards and S. K. Spurgeon, “Sliding Mode Control: Theory and Applications,” Taylor & Francis, Abingdon, 1998.
- [112] P.-K. Huang, P.-H. Shieh, F.-J. Lin and H.-J. Shieh, “Sliding-Mode Control for a Two-Dimensional PiezoPositioning Stage,” Control Theory & Applications, IET, Vol. 1, No. 4, 2007, pp. 1104-1113. doi:0.1049/iet-cta:20060371
- [113] J.-C. Shen, W.-Y. Jywe1, C.-H. Liu, Y.-T. Jian and J. Yang, “Sliding-Mode Control of a Three-Degrees-ofFreedom Nanopositioner,” Asian Journal of Control, Vol. 10, No. 3, 2008, pp. 267-276. doi:10.1002/asjc.33
- [114] J.-C. Shen, J.-C. Shen, H.-K. Chiang and Y.-L. Shu, “Precision Tracking Control of a Piezoelectric-Actuated System,” Precision Engineering, Vol. 32, No. 2, 2008, pp. 71-78. doi:10.1016/j.precisioneng.2007.04.002
- [115] Q. Xu and Y. Li, “Dynamics Modeling and Sliding Mode Control of an XY Micropositioning Stage,” The 9th International Symposium on Robot Control (SYROCO’09), Gifu, 9-12 September 2009, pp. 781-786.
- [116] Y. Li and Q. Xu, “Adaptive Sliding Mode Control with Perturbation Estimation and PID Sliding Surface for Motion Tracking of a Piezo-Driven Micromanipulator,” IEEE Transactions on Control Systems Technology, Vol. 18, No. 4, 2010, pp. 798-810. doi:10.1109/TCST.2009.2028878
- [117] H. C. Liaw, B. Shirinzadeh and J. Smith, “Sliding-Mode Enhanced Adaptive Motion Tracking Control of Piezoelectric Actuation Systems for Micro/Nano Manipulation,” IEEE Transactions on Control Systems Technology, Vol. 16, No. 4, 2008, pp. 826-833. doi:10.1109/TCST.2007.916301
- [118] X. Chen and T. Hisayama, “Adaptive Sliding-Mode Position Control for Piezo-Actuated Stage,” IEEE Transactions on Industrial Electronics, Vol. 55, No. 11, 2008, pp. 3927-3934. doi:10.1109/TIE.2008.926768
- [119] H. C. Liaw and B. Shirinzadeh, “Enhanced Sliding-Mode Constrained Motion Tracking Control of Piezo-Actuated Flexure-Based Mechanisms,” IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2009. AIM 2009, Singapore, 14-17 July 2009 2009, pp. 1879- 1884. doi:10.1109/AIM.2009.5229763
- [120] G. Schitter, P. Menold, H. F. Knapp, F. Allgower and A. Stemmer, “High Performance Feedback for Fast Scanning Atomic Force Microscopes,” Review of Scientific Instruments, Vol. 72, No. 8, 2001, pp. 3320-3327. doi:10.1063/1.1387253
- [121] M. S. Tsai and J. S. Chen, “Robust Tracking Control of a Piezoactuator Using a New Approximate Hysteresis Model,” Journal of Dynamic Systems, Measurement, and Control, Vol. 125, No. 1, 2003, pp. 96-102. doi:10.1115/1.1540114
- [122] G. Schitter, A. Stemmer, and F. Allgöwer, “Robust TwoDegree-of-Freedom Control of an Atomic Force Microscope,” Asian Journal of Control, Vol. 6, No. 2, 2004, pp. 156-163. doi: 10.1111/j.1934-6093.2004.tb00194.x
- [123] A. Sebastian and S. M. Salapaka, “Design Methodologies for Robust Nano-Positioning,” IEEE Transactions on Control Systems Technology, Vol. 13, No. 6, 2005, pp. 868-876. doi:10.1109/TCST.2005.854336
- [124] Y. Okazaki, “A Micro-Positioning Tool Post Using a Piezoelectric Actuator for Diamond Turning Machines,” Precision Engineering, Vol. 12, No. 3, 1990, pp. 151-156. doi:10.1016/0141-6359(90)90087-F
- [125] D. Croft, S. Stilson and S. Devasia, “Optimal Tracking of Piezo-Based Nanopositioners,” Nanotechnology, Vol. 10, No. 2, 1999, pp. 201-208. doi:10.1088/0957-4484/10/2/316
- [126] C. J. Li, H. S. M. Beigi, S. Li and J. Liang, “Nonlinear Piezo-Actuator Control by Learning Self Tuning Regulator,” Journal of Dynamic Systems, Measurement, and Control, Vol. 115, No. 4, 1993, pp. 720-723. doi:10.1115/1.2899203
- [127] H.-J. Shieh, F.-J. Lin, P.-K. Huang and L.-T. Teng, “Adaptive Tracking Control Solely Using Displacement Feedback for a Piezo-Positioning Mechanism,” IEE Proceedings——Control Theory and Applications, Vol. 151, No. 5, 2004, pp. 653-660. doi:10.1049/ip-cta:20040795
- [128] X. Tan and J. S. Baras, “Adaptive Identification and Control of Hysteresis in Smart Materials,” IEEE Transactions on Automatic Control, Vol. 50, No. 6, 2005, pp. 827-839. doi:10.1109/TAC.2005.849215
- [129] H. C. Liaw and B. Shirinzadeh, “Enhanced Adaptive Motion Tracking Control of Piezo-Actuated FlexureBased Four-Bar Mechanisms for Micro/Nano Manipulation,” Sensors and Actuators A: Physical, Vol. 147, No. 1, 2008, pp. 254-262. doi:10.1016/j.sna.2008.03.020
- [130] J.-H. Xu, “Neural Network Control of a Piezo Tool Positioner,” Canadian Conference on Electrical and Computer Engineering, Vancouver, 14-17 September 1993, pp. 333-336. doi:0.1109/CCECE.1993.332324
- [131] F.-J. Lin, H.-J. Shieh and P.-K. Huang, “Adaptive Wavelet Neural Network Control with Hysteresis Estimation for Piezo-Positioning Mechanism,” IEEE Transactions on Neural Networks, Vol. 17, No. 2, 2006, pp. 432-444. doi:10.1109/TNN.2005.863473
- [132] F.-J. Lin, H.-J. Shieh, P.-K. Huang and L.-T. Teng, “Adaptive Control with Hysteresis Estimation and Compensation Using RFNN for Piezo-Actuator,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 53, No. 9, 2006, pp. 1649-1661. doi:10.1109/TUFFC.2006.1678193
- [133] H. Numasato and M. Tomizuka, “Settling Control and Performance of a Dual-Actuator System for Hard Disk Drives,” IEEE/ASME Transactions on Mechatronics, Vol. 8, No. 4, 2003, pp. 431-438. doi:10.1109/TMECH.2003.819999
- [134] K. Leang and S. Devasia, “Hysteresis, Creep, and Vibration Compensation for Piezoactuators: Feedback and Feedforward Control,” Proceedings of the 2nd IFAC Conference on Mechatronic Systems, Berkley, 9-11 December 2002, pp. 283-289.
- [135] L. Y. Pao, J. A. Butterworth and D. Y. Abramovitch, “Combined Feedforward/Feedback Control of Atomic Force Microscopes,” Proceedings of the 2007 American Control Conference, New York City, 9-13 July 2007, pp. 3509-3515. doi:10.1109/ACC.2007.4282338
- [136] D. Croft and S. Devasia, “Vibration Compensation for High Speed Scanning Tunneling Microscopy,” Review of Scientific Instruments, Vol. 70, No. 12, 1999, pp. 4600- 4605. doi:10.1063/1.1150119
- [137] H. Hu, H. M. S. Georgiou and R. Ben-Mrad, “Enhancement of Tracking Ability in Piezoceramic Actuators Subject to Dynamic Excitation Conditions,” IEEE/ASME Transactions on Mechatronics, Vol. 10, No. 2, 2005, pp. 230-239. doi:10.1109/TMECH.2005.844705
- [138] C.-J. Lin and S.-R. Yang, “Modeling of a Piezo-Actuated Positioning Stage Based on a Hysteresis Observer,” Asian Journal of Control, Vol. 7, No. 1, 2005, pp. 73-80. doi:10.1111/j.1934-6093.2005.tb00230.x
- [139] S. S. Aphale, S. Devasia and S. O. Reza Moheimani, “High-Bandwidth Control of a Piezoelectric Nanopositioning Stage in the Presence of Plant Uncertainties,” Nanotechnology, Vol. 19, No. 12, 2008, pp. 125503.1- 125503.9. doi:10.1088/0957-4484/19/12/125503
- [140] D. Croft and S. Devasia, “Vibration Compensation for High Speed Scanning Tunneling Microscopy,” Review of Scientific Instruments, Vol. 70, No. 12, 1999, pp. 4600- 4605. doi:10.1063/1.1150119
- [141] S. Khan, M. Elitas, E. D. Kunt and A. Sabanovic, “Discrete Sliding Mode Control of Piezo Actuator in NanoScale Range,” IEEE International Conference on Industrial Technology, 2006. ICIT 2006, Mumbai, 15-17 December 2006, pp. 1454-1459. doi:10.1109/ICIT.2006.372418
- [142] J. Yi, S. Chang and Y. Shen, “Disturbance-ObserverBased Hysteresis Compensation for Piezoelectric Actuators,” IEEE/ASME Transactions on Mechatronics, Vol. 14, No. 4, 2009, pp. 4196-4201. doi:10.1109/TMECH.2009.2023986
- [143] S. Chang and S. Li, “A High Resolution Long Travel Friction-Drive Micropositioner with Programmable Step Size,” Review of Scientific Instruments, Vol. 70, No. 6, 1999, pp. 2276-2782. doi:10.1063/1.1149794
- [144] A. Bergander and J. Breguet, “Performance Improvements for Stick-Slip Positioners,” Proceedings of 2003 International Symposium on Micromechatronics and Human Science, Nagoya, 19-22 October 2003, pp. 59-66. doi:10.1109/MHS.2003.1249910
- [145] F. Castanos and L. Fridman, “Analysis and Design of Integral Sliding Manifolds for Systems with Unmatched Perturbations,” IEEE Transactions on Automatic Control, Vol. 51, No. 5, 2006, pp. 853-858. doi:10.1109/TAC.2006.875008
- [146] J. H. Painter, D. Kerstetter and S. Jowers, “Reconciling Steady-State Kalman and Alpha-Beta Filter Design,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 26, No. 6, 1990, 1990, pp. 986-991. doi:10.1109/7.62250
- [147] X. Wang, “High-Order Integral-Chain Differentiator and Application to Acceleration Feedback,” Submitted to Computer Science for Possible Publication, 2011.
- [148] A. Levant, “Robust Exact Differentiation via Sliding Mode Technique,” Automatica, Vol. 34, No. 3, 1998, pp. 379-384. doi:10.1016/S0005-1098(97)00209-4
- [149] Q. Xu and Y. Li, “Sliding Mode Control of a PiezoDriven Micropositioning System Using Extended Kalman Filter,” IEEE International Conference on Automation and Logistics (ICAL), 2010, Hong Kong and Macau, 16- 20 August 2010, pp. 427-432. doi:10.1109/ICAL.2010.5585322
- [150] J. L. Minase, T.-F. Lu and F. Wornle, “State Estimation of Nonlinear Piezoelectric Stack Actuator Hysteresis Model,” Proceedings of SPIE, Vol. 6414, 2006, pp. 641403.1-641403.10.
- [151] J. Minase, T.-F. Lu, B. Cazzolato and S. Grainger, “Adaptive Identification of Hysteresis and Creep in Piezoelectric Stack Actuators,” The International Journal of Advanced Manufacturing Technology, Vol. 46, No. 9-12, 2009, pp. 913-921. doi:10.1007/s00170-009-2033-8
- [152] F. Yang and R. W. Wilde, “Observers for Linear Systems with Unknown Inputs,” IEEE Transactions on Automatic Control, Vol. 33, No. 7, 1988, pp. 667-681. doi:10.1109/9.1278
- [153] M. Hou and P. C. Muller, “Design of Observers for Linear Systems with Unknown Inputs,” IEEE Transactions on Automatic Control, Vol. 37, No. 6, 1992, pp. 871-875. doi:10.1109/9.256351
- [154] S. Hui and S. Żak, “Observer Design for Systems with Unknown Inputs,” International Journal of Applied Mathematics and Computer Science, Vol. 15, No. 4, 2005, pp. 431-546.
- [155] S. H. Zak and S. Hui, S. “Output Feedback Variable Structure Controllers and State Estimators for Uncertain/Nonlinear Dynamic Systems,” IEE Proceedings D: Control Theory and Applications, Vol. 140, No. 1, 1993, pp. 41-50. doi:10.1049/ip-d.1993.0006
- [156] J.-L. Chang and T.-C. Wu, “Robust Disturbance Attenuation with Unknown Input Observer and Sliding Mode Controller,” Electrical Engineering, Vol. 90, No. 7, 2008, pp. 493-502. doi:10.1007/s00202-008-0099-1
- [157] T. Floquet, C. Edwards and S. K. Spurgeon, “On Sliding Mode Observers for Systems with Unknown Inputs,” International Journal of Adaptive Control and Signal Processing, Vol. 21, No. 8-9, 2007, pp. 638-656. doi:10.1002/acs.958
- [158] K. Kalsi, J. Lian, S. Hui and S. H. Zak, “Sliding-Mode Observers for Systems with Unknown Inputs: A HighGain Approach,” Automatica, Vol. 46, No. 2, 2010, pp. 347-353. doi: 10.1016/j.automatica.2009.10.040
- [159] X. Liu, J. Jeong and J. Kim, “A Three Translational DoFS Parallel Cube-Manipulator,” Robotica, Vol. 21, No. 6, 2003, pp. 645-653. doi:10.1017/S0263574703005198
- [160] Q. Xu, and Y. Li, “A Novel Design of a 3-PRC Translational Compliant Parallel Micromanipulator for Nanomanipulation,” Robotica, Vol. 24, No. 4, 2006, pp. 527-528. doi:10.1017/S0263574705002559
- [161] Y. Yue, F. Gao, X. Zhao and Q. Jeffrey Ge, “Relationship among Input-Force, Payload, Stiffness and Displacement of a 3-DOF Perpendicular Parallel Micro-Manipulator,” Mechanism and Machine Theory, Vol. 45, No. 5, 2010, pp. 756-771. doi:10.1016/j.mechmachtheory.2009.12.006
- [162] S. Awtar and A. Slocum, “Constraint-Based Design of Parallel Kinematic XY Flexure Mechanisms,” Journal of Mechanical Design, Vol. 129, No. 8, 2007, pp. 816-830. doi:10.1115/1.2735342
- [163] Q. Yao, J. Dong and P. Ferreira, “A Novel ParallelKinematics Mechanisms for Integrated, Multi-Axis Nanopositioning: Part 1. Kinematics and Design for Fabrication,” Precision Engineering, Vol. 32, No. 1, 2008, pp. 7- 19. doi:10.1016/j.precisioneng.2007.03.001
- [164] J. Dong, Q. Yao and P. Ferreira, “A Novel ParallelKinematics Mechanism for Integrated, Multi-Axis Nanopositioning: Part 2: Dynamics, Control and Performance Analysis,” Precision Engineering, Vol. 32, No. 1, 2008, pp. 20-33. doi:10.1016/j.precisioneng.2007.03.002
- [165] J. Dong, S. Salapaka and P. Ferreira, “Robust Control of a Parallel-Kinematic Nanopositioner,” Journal of Dynamic Systems, Measurement, and Control, Vol. 130, No. 4, 2008, pp. 041007.1-041007.15. doi:10.1115/1.2936861
- [166] Y. Tian, B. Shirinzadeh and D. Zhang, “A Flexure-Based Five-Bar Mechanism for Micro/Nano Manipulation,” Sensors and Actuators A: Physical, Vol. 153, No. 1, 2009, pp. 96-104. doi: 10.1016/j.sna.2009.04.022
- [167] Y. Tian, B. Shirinzadeh and D. Zhang, “Design and Dynamics of a 3-DOF Flexure-Based Parallel Mechanism for Micro/Nano Manipulation,” Microelectronic Engineering, Vol. 87, No. 2, 2010, pp. 230-241. doi:10.1016/j.mee.2009.08.001
- [168] K. Hu, J. Kim, J. Schmiedeler and C. Menq, “Design, Implementation, and Control of a Six-Axis Compliant Stage,” Review of Scientific Instruments, Vol. 79, No. 2, 2008, pp. 025108.2-025105.11. doi:10.1063/1.2841804
- [169] T. W. Seo, D. S. Kang and J. Kim, “Synthesis and Comparison of Fine Actuator Controllers for a 3-DOF Micro Parallel Positioning Platform,” Proceedings of the 10th International Conference on Control, Automation, Robotics and Vision, Hanoi, 17-20 December 2008, pp. 1606- 1611. doi:10.1109/ICARCV.2008.4795765
- [170] M. Grotjahn, B. Heimann and H. Abdellatif, “Identification of Friction and Rigid-Body Dynamics of Parallel Kinematic Structures for Model-Based Control,” Multibody System Dynamics, Vol. 11, No. 3, 2004, pp. 273-294. doi:10.1023/B:MUBO.0000029426.05860.c2

