Open Journal of Biophysics
Vol.07 No.02(2017), Article ID:75791,11 pages
10.4236/ojbiphy.2017.72005
Dynamics Study of the Deformation of Red Blood Cell by Optical Tweezers
Konin E. Jean Michel1,2, Yale Pavel1, Megnassan Eugene2, Michel A. Kouacou1, Jeremie T. Zoueu1
1Laboratoire d’Instrumentation Image et Spectroscopie, UMRI EEA, INP-HB, Yamoussoukro, Cote d’Ivoire
2Laboratoire de Physique Fondamentale et Appliquée, UNA, Abidjan, Cote d’Ivoire

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 11, 2017; Accepted: April 26, 2017; Published: April 29, 2017
ABSTRACT
In recent years, extensive research has been carried out on red blood cells in order to investigate their mechanical properties. The interest in these studies has been possible thanks to the technological innovations made in the field of micro or nano manipulation of biological and non-biological particles without physical contact. In the present project, we have developed a new approach to study the deformation of red blood cells moving against a trapped microbead by applying a sinusoidal voltage (DC offset 3.5 Vpp) to the stage at 0.4 Hz frequencies. The oscillating movement imposed on the stage highlights the indentation test and the tensile test known for the study of mechanical behavior of materials. The mechanical properties found are: the modulus of elasticity (Young Modulus), the shear modulus, the coefficient of hardening and erythrocyte resistance coefficient. The axial shear modulus 25.00 ± 1.5 μN/m and the transversal shear modulus 15.7 ± 4.63 μN/m were compared to those in the literature. These values were respectively determined by Hooke’s law and the Hertz model.
Keywords:
Optical Tweezers, Elasticity, Mechanical Properties, Tensile, Indentation

1. Introduction
The red blood cell’s main function is the transport of gas through the body [1] [2] . It is responsible for oxygen transport and the transport of carbon dioxide to the lungs. To accomplish this function, it travels hundreds of kilometers through the body [3] . During its travel, the red blood is subjected to very high shear, and must sometimes traverse capillaries whose inner diameter is as small as 3 µm and it needs to deform considerably to enter the capillaries [4] , indicating the importance of their deformability. Red blood cell deformability is one of the major factor determining the flow properties of the blood as well as an important factor in regulating blood circulation [5] . The reduction of red cell deformability increases the blood viscosity and reduces oxygen transport to organs and tissues. And due to the remarkable property of its membrane (elasticity), and its biconcave form, the red blood cell reaches through capillaries without being altered in order to regain its original shape. However, some diseases such as malaria, cancer and sickle cell anemia affect this property causing malfunction of the organism [3] . These infections are accompanied by profound changes in the mechanical properties of the infected red blood cells, contributing to reduced blood flow in the microcirculation. Several studies have been conducted to determine modulus elasticity [6] [7] . The study of the elasticity of red blood cells is a very promising field of research for the diagnosis of certain diseases such as cancer and malaria. Among these technological innovations, the optical tweezers are an essential tool for the manipulation of nanoparticles. This has been demonstrated by several publications in the field of manipulation of small and relatively transparent particles using optical tweezers after the first reports by Arthur Ashkin [8] [9] . The success of optical tweezers is largely supported by the high quality of the fundamental work already existing in the fields of physics, biochemistry and biology [10] [11] . Therefore, it is of paramount importance to continue developing new approaches for determining the mechanical properties of red blood cells through the optical tweezers.
In the proposed method, the red blood cells are first deformed and then stretched out by applying a sinusoidal voltage to the stage. The originality of this work is the realization of the indentation and tensile tests through a microbead to study the mechanical property of red blood cell. The implementation of this method does not require special arrangement. There are a few reports using optical tweezers on human red blood cells, in particular the work done by Guillaume Lenormand [12] . This researcher determined the elasticity of red blood cells by attaching two microbeads on the membrane of the cell. By applying two forces on the microbead the elasticity of the human red blood cell was calculated and the values underestimated with respect to those obtained when using aspiration by micropipette. It should be noted that in this previous reported experiment special setups are needed and the microbead adhere irreversibly to the membrane. In our approach, there is no need of any special arrangement to study the elasticity of the red blood cells.
2. Material and Methods
2.1. Experimental Setup
As part of this work we have used a photonic microscope according to an inverse microscope configuration from the kit of the optical tweezers of Thorlabs [13] as shown in Figure 1. This device is equipped with a near infrared laser diode (PL980P330J, λ = 980 nm); this laser diode is used for the trapping through an immersion oil lens (Nikon 100X immersion, NA = 1.25 Working distance 0.23 mm) with a maximum power of 330 mW power. The transmitted laser beam is

Figure 1.(a) Optical tweezers setup for cell indentation and force measurement [7] . Laser trapping (980 nm) beam path (red) and bright-field imaging path (bleu). PS: 3-axis nano-piezo stage; TL: Tube Lens, L1 - L2 convergent lenses; DCM1-2 dichroic mirrors, TC: holder, QPD: Quadrant Photo Detector, Low-Frequency Generator (GFL), TC: temperature controller, LDC: Laser Diode Controller, PC: Computer (b) illustration of the different axes OXYZ: the vector k indicates the meaning the spread of laser.
collected by an immersion air condenser (Nikon 10X, NA 0.25, WD 7) which conveys the signal to the photodiode quadrant detector QPD (Thorlabs, PDQ80A, detector size 7.8 mm). We have coupled the device with a digital oscilloscope and a Low-Frequency Generator (GFL), the signal produced by the photodiode is first amplified by an amplifier. The movement of the micro-particles is observed through a CCD camera (Thorlabs DCU224C). The lamella is placed on a manual three axes translation plate which can be moved with greater precision by a piezoelectric controller along these three axes. This device comprises in its interior two movable mirrors that can guide the beam and two semi-reflective dichroic mirrors. The sample illumination is provided by a LED white source.
2.2. Sample Preparation Protocol
We collected 0.5 μl of blood and 0.4 µl of bead of diameter 2 µm in a 5 ml saline solution.
2.3. Experimental Implementations
This method consists of trapping a microbead, and creating a contact between the microbeads already trapped and a moving red blood cell. We applying a sinusoidal voltage (DC offset 3.5 Vpp) using a function generator on the stage along the Oz axis (the oscillation frequency is 4 Hz). Then we increased the laser power while recording the residual diameter of the red blood cell. The sinusoidal oscillation applied to the stage along the Oz axis is responsible for the indenta- tion. When both microbead and erythrocyte are in the same plane, the blood cell tend to substitute to the microbead in the trapped causing its deformation. The pressure is released when the red blood is moved up or down together with the oscillation.
2.4. Data Acquisition Method
Data were acquired by video microscopy. This method of acquisition provides further information to calculate the strength and the stiffness constant. It consists of recording the bead trapped as well as the red blood cell trying to enter the trap. The different displacement along the Oz axis HD of the microbead in the trap were analyzed by Image J software after the calibration of the CCD camera. These different positions of the microbead allowed determining the stiffness throughout the equipartition theorem given by the following equation:
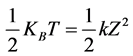 (1)
(1)
 (2)
(2)
where  is the Boltzmann constant and T the temperature.
is the Boltzmann constant and T the temperature.
Then the Hooke’s law was used to calculate the force exerted by the bead on the red blood cell.
 (3)
(3)
where HD is the displacement of the microbead along the Oz axis. After determining the force along Oz and Ox axis, the modulus of elasticity through the tensile and the indentation tests can be determined.
2.5. Modulus of Elasticity Measurement
2.5.1. The Tensile Method
The red blood cell is initially deformed by the trap as the consequence of the radiation stress distribution. After the deformation of the red blood cell, it is unconstrained and the trapped is moved to the microbead; a contact is created between the trapped microbeads and the moving deformed red blood cell. The application of the sinusoidal voltage to the stage along the Oz axis led the red blood cell to tensile stress by indentation. The initial diameter or width lo represent the red blood cells (Figure 2(a)) prior to the application of the sinusoidal voltage and l is the width of the blood cell after application of the sinusoidal voltage (Figure 2(b)). As the laser power is increased, the diameter l of the red blood cell is stretched and subsequently recorded. Transversal width of red blood cell increases and the longitudinal length of red blood cell decreases (Figure 2(b)).
And the representation of the conventional tensile diagram, constraint  to the deformation e are respectively defined by:
to the deformation e are respectively defined by:
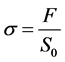 (4)
(4)

Figure 2. Illustration of the tensile: (a) deformation of red blood cell (l0: initial width) and (b) stretching of red blood cell (l: width of stretching).
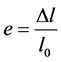 (5)
(5)
where 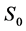 is the surface of red blood cell. These Equations (4) and (5) allow us to determine the red blood cell elasticity modulus as well as the rational diagram of tensile diagram which is the true stress σ taking into account the variation of the section during the test, according to the true strain ε defined respectively by:
is the surface of red blood cell. These Equations (4) and (5) allow us to determine the red blood cell elasticity modulus as well as the rational diagram of tensile diagram which is the true stress σ taking into account the variation of the section during the test, according to the true strain ε defined respectively by:
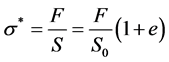 (6)
(6)
 (7)
(7)
Through the tensile test the Poisson’s ratio may be determine according to the following relationship:
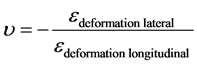 (8)
(8)
2.5.2. The Conventional Indentation Method
The study of material behavior requires knowledge the mechanical properties of the surfaces in contact. The indentation test allows easy estimation of the elastic, plastic and viscoelastic properties of materials in contact at microscopic scale. The main properties measured are the hardness and the modulus of elasticity of the material. In Figure 3, we describe the principle of this technique which is based on moving the red cell membrane against a trapped bead (or indenter). The driving height (He) is determined according to the Formula [14] .
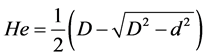 (9)
(9)
where D and d are respectively, the diameter of the bead and the remaining diameter indenter.
This method determines the Brinell hardness:
 (10)
(10)

Figure 3. Illustration of the indentation: (a) experimental procedure of Brinell hardness; (b) pressing the microbeads of 2 µm in diameter in the red blood cell membrane
The surface area of the spherical cap  by the ball indenter is a function of the diameter D of the microbead and the residual cavity d. The surface is calculated by the following formula.
by the ball indenter is a function of the diameter D of the microbead and the residual cavity d. The surface is calculated by the following formula.
 (11)
(11)
Then we can deduce the Brinell hardness according to the formula below:
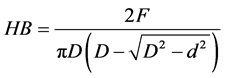
And the modulus of elasticity through the Hertz model is given by the Equation [15] .
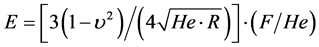
where R is the radius of the microbead and F the force along the Ox axis.
3. Results and Discussion
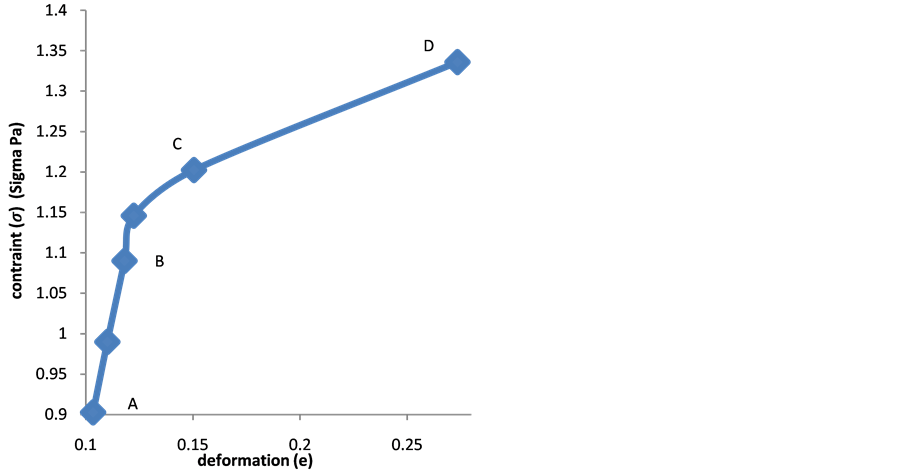
Figure 3(a) and Figure 3(b) show that the red blood cell membrane is deformed while trying to get in the trap already occupied by the microbead; this deformation will increase with the photonic force (Figure 4(a) and Figure 4(b)). On the graph, the linear range AB corresponds the linear elasticity, or the elastic domain of reversible deformation (σ = Ee), where E is the Young’s modulus; the range corresponding to BC is related to the plastic deformation. Using the stress-strain curve the Young’s modulus was calculated as 12.85 ± 0.9 N/m2 or 12.85 ± 0.9 Pa. The limit of elasticity could be taken equal to the proportional limit. This yield point is also calculated directly from the convention curve (Figure 4(a)) of the point B.
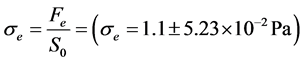
A loss of linearity is observed in the so-called plastic range (BC). There is a change from the elastic region to the plastic area because in the elastic region the variation is small, it exhibits a proportionality between the deformation and the stress contrary to the plastic area.
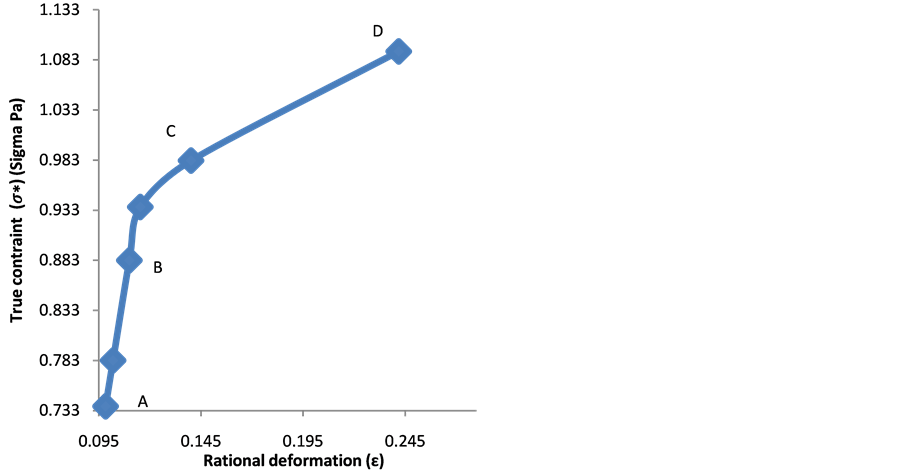
Figure 4. (a) Dependency of deformation with the contraint; (b) and dependency of rational deformation with true constraint.
The Figure 4(a) and the graph of Figure 4(b) haven't the same origins; however they behave similarly. The Equation (15) shows a shift between the true stress curve and the conventional stress curve in the case where the strain is different to zero (e ≠ 0).

Therefore, the graph of the Figure 4(b) fits well with the Equation (15). It may be noted that there is no difference between the conventional diagram and rational diagram (Figure 4(a)) in the elastic range since the deformation is low. In contrast, in the domain of the plastic deformation of rational diagram curve takes a parabolic shape (Figure 4(b)). The range (BD) of the rational curve diagram can be put in a mathematical form. The formula used is Hollomon equation:

where n the coefficient of work hardening (strain hardening factor) or consolidation defines the ability of red blood cell to deform by expanding and distributing the deformation. As shown in Figure 2, we found that during the test, the red blood cell deformed gradually resumed the spherical shape and that as the applied force intensified the deformation was small in the area of plasticity, which might lead us to think about the phenomenon of hemolysis of the point D. And k is the coefficient of resistance of the red blood cell.
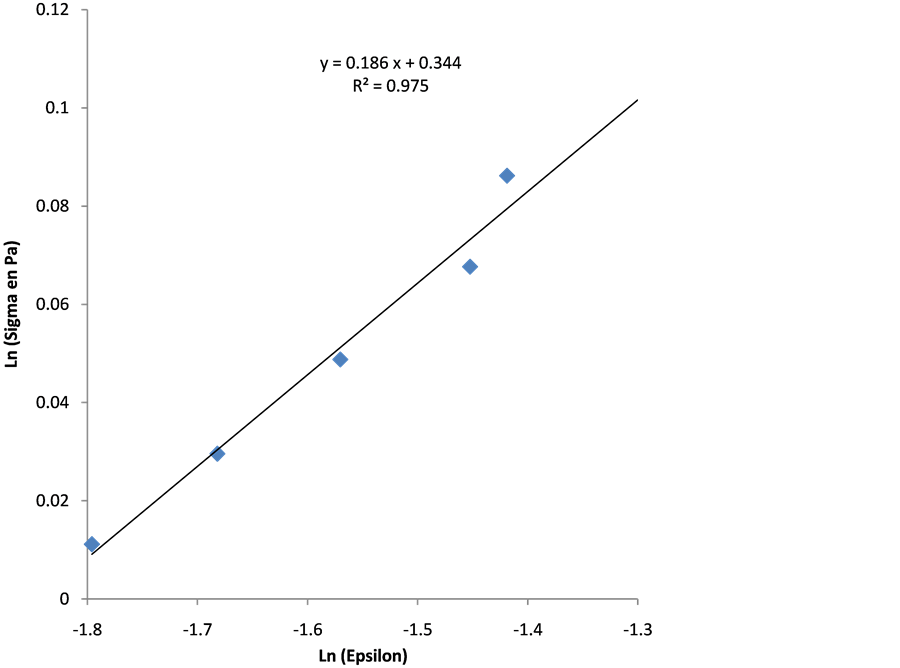
Determination of Strain Hardening Exponent n and the Resistance Coefficient k
In the Hollomon equation, the plot of the line 
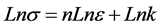
This Equation (16) allows us to determine the parameters n and k through linear regression model of the Figure 5 which are respectively 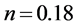
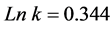
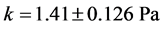

In the Figure 5 the fitting is quite good, with coefficient of determination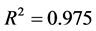

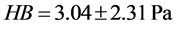
(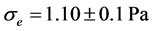
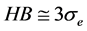
and confirms the reliability of this new approach.
The elasticity obtained by the tensile is 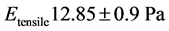
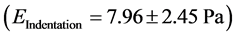
Figure 5. Linear model of regression between Ln (sigma Pa) and Ln (epsilon).

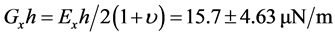
4. Conclusion
Through this approach we have been able to demonstrate two tests which are indentation and tensile in order to obtain a wide range of mechanical properties of the red blood cell. Such us elasticity, shear modules, hardness, resistance coefficient we find that this approach can be use to determine the mechanical property of biology cells. This method is simple to carry out; getting the red blood cell and microbead to be in contact doesn’t require any special arrangement neither for the preparation of the microbeads nor for the preparation of the red blood cell. Compared with the values obtained by the method of tensile and that of the indentation which are in accordance with the theories available, and also with respect to those of the literature, we can state that our approach is suitable for the mechanical properties of biological studies.
Acknowledgments
We would like to sincerely thank ISP and TWAS for funding of our research work.
Cite this paper
Michel, K.E.J., Pavel, Y., Eugene, M., Kouacou, M.A. and Zoueu, J.T. (2017) Dynamics Study of the Deformation of Red Blood Cell by Optical Tweezers. Open Journal of Biophysics, 7, 59-69. https://doi.org/10.4236/ojbiphy.2017.72005
References
- 1. Chasis, J.A. and Stephen, B. (1987) Shohet Red Cell Biochemical Anatomy and Membrane Properties. Annual Review of Physiology, 49, 237-248.
https://doi.org/10.1146/annurev.ph.49.030187.001321 - 2. Wagner, P.D. (1977) Diffusion and Chemical Reaction in Pulmonary Gas Exchange. Physiological Reviews, 57, 257-312.
- 3. Schmid-Schönbein, G.W., Fischer, T., Driessen, G. and Rieger, H. (1979) Micro-manipulation Clinical Research Applications of Engineering Principals. 333-417.
- 4. Lim, C.T., Dao, M., Suresh, S., Sow, C.H. and Chew, K.T. (2004) Large Deformation of Living Cells Using Laser Traps. Acta Materialia, 52, 1837-1845.
https://doi.org/10.1016/j.actamat.2003.12.028 - 5. Chien, S. (1987) Red Cell Deformability and Its Relevance to Blood Flow. Annual Review of Physiology, 49, 177-192.
https://doi.org/10.1146/annurev.ph.49.030187.001141 - 6. Bareil1, P.B., Sheng, Y., Chen, Y.-Q. and Chiou, A. (2007) Calculation of Spherical Red Blood Cell Deformation in a Dual-Beam Optical Stretcher. Optics Express, 15, 16029-16034.
https://doi.org/10.1364/OE.15.016029 - 7. Yousafzai, M.S., Ndoye, F., Coceano, G., Niemela, J., Bonin, S., Scoles, G. and Cojoc, D. (2015) Substrate-Dependent Cell Elasticity Measured by Optical Tweezers Indentation. Optics and Lasers in Engineering, 76, 27-33.
https://doi.org/10.1016/j.optlaseng.2015.02.008 - 8. Ashkin, A. and Dziedzic, J. (1987) Optical Trapping and Manipulation of Viruse Sand Bacteria. Science, 235, 1517-1520.
https://doi.org/10.1126/science.3547653 - 9. Ashkin, A., Dziedzic, J. and Yamane, T. (1987) Optical Trapping and Manipulation of Single Cells Using Infra-Red Laser Beams. Nature, 330, 769-771.
https://doi.org/10.1038/330769a0 - 10. Neuman, K.C. and Block, S.M. (2004) Optical Trapping. Review of Scientific Instruments, 75, 2787-2809.
https://doi.org/10.1063/1.1785844 - 11. Ashok, P.C. and Dholakia, K. (2012) Optical Trapping for Analytical Biotechnology. Current Opinion in Biotechnology, 23, 16-21.
https://doi.org/10.1016/j.copbio.2011.11.011 - 12. Lenormand, G. (2001) Elasticity of a Human Red Blood Cell Study by Optical Tweezers. Ph.D. Thesis, Physical Option Liquids Sustained.
- 13. MOTKwtc.
https://www.thorlabs.com/NewGroupPage9.cfm?ObjectGroupID=3959 - 14. Pertuz, A. (2003) Indentation of Vickers and Knoop Massive or Coated Materials: Hardness, Toughness and Adhesion. Ph.D. Thesis.
- 15. Nawaz, S., Sánchez, P., Bodensiek, K., Li, S., Simons, M., Schaap, I.A. (2012) Cell Visco-Elasticity Measured with AFM and Optical Trapping at Sub-Micrometer Deformations. PloS One, 7, e45297.
https://doi.org/10.1371/journal.pone.0045297 - 16. Bhushan, B. (2002) Introduction to Tribology. John Wiley & Sons, Hoboken.
- 17. Dao, M., Li, J., Suresh, S. (2006) Molecularly Based Analysis of Deformation of Spectrin Network and Human Erythrocyte. Materials Science and Engineering, 26, 1232 -1244.
https://doi.org/10.1016/j.msec.2005.08.020 - 18. Guck, J., Ananthakrishnan, R., Mahmood H., Moon, T.J., Cunningham, C.C. and Käs, J. (2001) The Optical Stretcher: A Novel Laser Tool to Micromanipulate Cells. Biophysical Journal, 81, 767-784.
https://doi.org/10.1016/S0006-3495(01)75740-2 - 19. Hénon, S., Lenormand, G., Richert, A. and Gallet, F. (1999) A New Determination of the Shear Modulus of the Human Erythrocyte Membrane Using Optical Tweezers. Biophysical Journal, 76, 1145-1151.
https://doi.org/10.1016/S0006-3495(99)77279-6 - 20. Yu, L., He, Y., Chiou, A. and Sheng, Y. (2011) Deformation of Biconcave Red Blood Cell in the Dual-Beam Optical Tweezers. Proceedings of the 2011 COMSOL Conference, Boston.
- 21. Rancourt-Grenier1, S., Wei, M.-T., Bai, J.-J., Chiou, A., Bareil1, P.P., Duval1, P.-L., and Sheng, Y. (2010) Dynamic Deformation of Red Blood Cell in Dual-Trap Optical Tweezers. Optics Express, 18, 10462.
https://doi.org/10.1364/OE.18.010462