Open Journal of Metal
Vol.05 No.04(2015), Article ID:63265,10 pages
10.4236/ojmetal.2015.54005
A Simplified Microcontroller Based Potentiostat for Low-Resource Applications
Bolaji Aremo1*, Mosobalaje Oyebamiji Adeoye1, Imoh Bassey Obioh2, Odunayo Adetola Adeboye3
1Department of Materials Science and Engineering, Obafemi Awolowo University, Ile-Ife, Nigeria
2Centre for Energy Research and Development, Obafemi Awolowo University, Ile-Ife, Nigeria
3Department of Agricultural Engineering, Obafemi Awolowo University, Ile-Ife, Nigeria
Email: *bolaji_aremo@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 December 2015; accepted 26 January 2016; published 29 January 2016
ABSTRACT
A low component count, microcontroller-based potentiostat circuit was developed through the use of operational amplifiers arranged in different feedback configurations. This was developed to alleviate the cost burden of equipment procurement in low-cost and budget applications. Simplicity was achieved in the design by the use of the microcontroller’s native functionalities and a low-cost R/2R resistor ladder digital-to-analogue converter. The potentiostat was used to investigate the Ni2+/Ni(s) redox couple in a 3-electrode cell with a silver/silver chloride reference electrode and graphite counter and working electrodes. Linear sweep voltammograms were obtained at scan rates of 10, 20, 30 and 40 mV/s. The analysis of the peak current versus (scan rate)1/2 plot indicated that the Ni2+/Ni(s) reduction, though conforming to the Randles-Sevcik equation, was a non- reversible redox reaction.
Keywords:
Potentiostat, Voltammogram, Microcontroller, Randles-Sevcik, Scan Rate

1. Introduction
The potentiostat has remained the work-horse of the electrochemistry laboratory ever since the development of the first 3-electrode cell by Hickling in the early 1940s. Using Hickling’s original ideas, many incarnations of the device have been produced for different specialized applications over the years from basic electrochemical redox investigations [1] [2] to electrochemical sensors used in biomedical implants [3] .
Potentiostat circuits are of widely varying complexities, often dictated by the intended use. A key distinguishing feature is the current measurement range. It is almost impossible to have a single system capable of current measurement across a wide range, from the sub pico-ampere up to the ampere range due to the different circuit architectures required. Auto-ranging resistors have been employed as a solution to achieve multi-current measurement capabilities [4] [5] . This feature and the supporting circuits however contribute to the cost of the instrumentation. As the required current range increases even such measures often become impractical. Additional circuit features required for precision potentiostat control may also result in increased circuit complexity and cost. Read noise minimization circuits [6] [7] sometimes added to reduce “ringing” or oscillation, invariably increase system costs. Modern potentiostat circuits range in prices from about $2500 to $25,000 [8] , with a median price of about $10,000 for decent laboratory units.
The potentiostat is fast ceasing to be the prime preserve of the electrochemistry laboratory. It is quickly making inroad into industrial and consumer devices. Potentiostat circuits can be found embedded in various gas sensors [9] , electronic “tongue” in the food industry [10] and environmental monitoring devices [11] .
The demand for “embedded” and specialized potentiostat circuits is bound to continue. This has inspired the development by many workers of simplified, low cost instrumentation that do away with the bells and whistles, while retaining core potentiostat functionalities. A field-portable, low-foot print design is described in [12] , while a do-it-yourself unit that is capable of a wide range of electrochemical investigations is reported in [13] .
In the simplified design reported here, otherwise expensive components are replaced with low-cost, simplified circuit architecture. It is believed that the low component count, and low cost of this design will contribute further to making the potentiostat ubiquitous in low-resource electrochemical laboratories and in budget products and applications.
2. Methodology
2.1. The Potentiostat System
A schematic representation of the potentiostat system is presented in Figure 1. The ADC was required for process data acquisition and caching by software. Level shifters “bridge” different segments of the circuit. These were configured as bipolar-to-unipolar converters and unipolar-to-bipolar converters. The level shifters transform voltage signal produced in one circuit module (e.g. single or dual rail voltage) into a form required in another circuit module.
A C-Sharp based software interface was developed in-house for data acquisition and control of the circuit. The data acquired were exported to spread sheet programs for detailed analysis.
Figure 1. Schematic representation of the potentiostat system.
2.2. Description of Circuit Modules
In summary the main parts of the potentiostat circuit are: 1) The potentiostat control circuit; 2) Digital-to-Ana- logue-Converter circuit; 3) PIC18F452 Microcontroller (MicroChip Inc., Arizona USA); 4) AC/DC full wave rectifier circuit; 5) Voltage level shifters; and 6) Current-to-voltage converter.
2.2.1. The Potentiostat Control Circuit
The potentiostat control circuit is presented in Figure 2. In the figure, CE is the Counter Electrode, RE is the Reference Electrode, and WE is the Working Electrode. The main modules of this circuit are described as follows.
1) Module A
Module A is a differential amplifier. The operational amplifier (op-amp) amplifies the voltage difference between the non-inverting input and the inverting input. This can be described by the following equations:
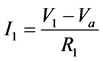 (1)
(1)
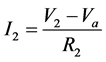 (2)
(2)
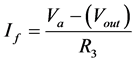 (3)
(3)
At the summing point,
 (4)
(4)
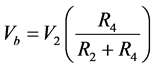 (5)
(5)
Figure 2. The potentiostat control circuit.
If V2 = 0, then
 (6)
(6)
If V1 = 0, then
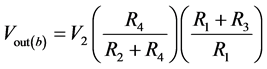 (7)
(7)
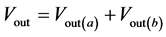 (8)
(8)
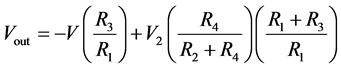 (9)
(9)
When R1 = R2 and R3 = R4, then
 (10)
(10)
If all the resistors are of the same value, that is R1 = R2 = R3 = R4, then the circuit becomes a unity gain differential amplifier.
2) Module B
In Module B, the voltage output from module A is fed into the non-inverting input of op-amp 2 while the op-amp’s inverting input was directly connected to its output. Op-amp 2 was configured as a voltage follower. This effectively isolates the input from the output to prevent loading of the input signal. The voltage output from op-amp 2 was connected to the CE.
3) Module C
Module C comprises op-amp 3 configured as a voltage follower. This is an additional measure to prevent current flow through the RE. Current flow through the RE will polarise it, rendering it unreliable. Point Z in this module is a connection to a level shifter circuit. The level shifter’s task is to transform the voltage at Z into the 0 to +5 V range required by the microcontroller for the measurement of the RE’s potential.
4) Module D
Module D is the current measurement module based on the feedback ammeter principle. Here, the input current flows through the feedback resistor (Rf = 100 Ω). The low offset current of the op-amp changes the current (Iin) by a negligible amount. Thus, the output voltage is a measure of the input current, and sensitivity is determined by Rf. Op-amp 4 is tied to real ground; voltage perturbations coming from the WE forces the op-amp to output a voltage of equal but opposite polarity through the 100 Ω resistor. This action forces the potential values at the op-amps inputs to the same value of zero. This feedback voltage is also measured at Y. From this point it is transmitted to the level shifter for eventual connection to the microcontroller’s ADC.
2.2.2. The DAC-Use of the R/2R Ladder Circuit
A typical R/2R resistor ladder is illustrated in Figure 3. In this circuit, the digital output word emanating from
Figure 3. The R/2R resistor ladder circuit.
the microcontroller’s I/O ports are connected to  in the diagram. The eventual voltage output, Vout, in the figure is computed by the use of the following equation:
in the diagram. The eventual voltage output, Vout, in the figure is computed by the use of the following equation:
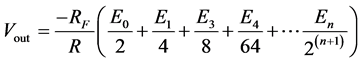 (11)
(11)
In this manner, the voltage value from the microcontroller’s on-board program (converting voltage value into binary equivalents of 0 s and 1 s) is converted to its actual analogue equivalent. This physical equivalent, called the control voltage, represents the actual voltage value desired. It is this voltage that is connected to point X in Module A (see Figure 2).
2.3. Investigation of the Ni2+/Ni Reduction Reaction
An investigation of the Ni2+/Ni reduction reaction was carried out by using linear sweep voltammetry (LSV). This was done in a 3-electrode cell with a silver/silver chloride reference electrode and graphite working and counter electrodes. The surface area of the working electrode was 0.12568 cm2. The experiment was carried out by using a 1 M solution of nickel sulphate (BDH Chemicals, Poole England) prepared with distilled water. The surfaces of the graphite counter and working electrodes used were polished to rid it of any adsorbed films and rinsed in de-ionised water. LSV was carried out at four different scan rates of 10, 20, 30 and 40 mV/s within a potential window of between −0.1 and −1.5 V (vs. Ag/AgCl).
3. Results and Discussion
3.1. Operation of the Potentiostat
The complete potentiostat circuit is presented in Figure 4. In Figure 4, op-amp 1 was configured as an inverting amplifier. The non-inverting input of the op-amp was tied to real ground while the inverting input at point A, strove to become a virtual ground. This was achieved when the op-amp output an inverted value of Vin. The op-amp sent the inverted quantity in a feedback loop, through the test solution and the reference electrode, back to the inverting input. At point A in the inverting input, both the original and inverted values of Vin combined to give a net potential of zero. By this the potential difference between the inverting and non-inverting inputs of op-amp 1 became zero. In this way, op-amp 1 succeeded in applying the control voltage (Vin) to the counter electrode. However, the reference and working electrodes were connected together by virtue of being immersed in the same ionically conducting solution.
The potential (with respect to ground) at both the working and reference electrodes is equal in magnitude but opposite that applied to the counter electrode by op-amp 1. The potential applied to the counter electrode by op-amp 1 appeared at the working electrode through conduction by charged ionic species in the test solution. In order to have the same potential on the working electrode, the applied potential at the counter electrode caused a quantity of charged species (ions), equivalent to the applied potential, to be produced or consumed at the counter electrode. The ionic species produced were the current conductors in the solution and were conducted towards the working electrode, under the influence of potential difference. At the working electrode, the ionic conductors were exchanged for electrons at the electrode’s surface.
In the circuit, provision was made for measuring the small exchange current. This was accomplished via op-amp 2, which was configured as a feedback ammeter. The feedback ammeter produces an output voltage equivalent of the exchange current. Op-amp 3 is used as a voltage follower and acts as a buffer for the reference electrode to prevent current flow through it. The buffer was essential to keep the potential at the reference electrode constant. This was naturally achieved in op-amp 3 due to its inherently large input impedance (several mega Ohms). Thus, current could not flow from the input to the output of the op-amp. It instead, followed the path of least resistance, which was through the working electrode. It also acted as an inverting voltage follower, producing an inverted output of the reference electrode potential for onward summing at point A, for the attainment of virtual ground.
3.2. Output Voltage and Current
The microcontroller is capable of producing voltage in the range of 0 - 5000 mV through the R/2R ladder network. It was then level-shifted to between −2500 mV and +2500 mV. This gives a voltage output range of 5000
Figure 4. The complete potentiostat circuit.
mV. The microcontroller’s 10 bit ADC reads this voltage at the following resolution:

Also, in Module D (Figure 2) current is measured through the combination of op-amp 4 and Rf which together function as a current-to-voltage converter. The voltage drop across Rf (measured at point Y) was connected to one of the microcontroller’s ADC channels. The current was eventually determined by the implementation of Ohm’s law in the control software program based on the measured voltage and the value of Rf.
The current measurement resolution depends on the voltage read resolution of the microcontroller’s ADC (5 mV calculated in Equation (12)), and the value of Rf (i.e. 100 Ω). The minimum current detectable by the potentiostat circuit was thus determined using Ohm’s law as follows:

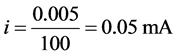
Or, considering positive and negative voltage perturbations,

The maximum current measured by the circuit is similarly determined by applying Ohm’s law to the maximum voltage value measurable (2500 mV) and the value of RF. Hence, the maximum current measurable by the potentiostat is,

Considering positive and negative voltage perturbations,

The incorporation of 16-bit and higher precision ADC units would seem to suggest an automatic attainment of higher resolution. While this prospect is attractive, the actual reality is however different. At 16-bit resolution and a Full Scale Range of 5 V (5000 mV), the voltage resolution is about 76 µV. This opens upnumerous problems related to circuit instability and noise. Guaranteeing this sort of accuracy with digital switching current emanating from a microcontroller is not a task easily achieved without costs. The use of a higher precision ADC (in a microcontroller) comes with the added responsibility of additional circuit components such as the incorporation of a separate chip with separate filtered power, and stringent circuit assembly protocol. Even ordinarily mundane tasks such as soldering and the physical sizes of resistors become very serious considerations that are necessary to ensure stability. Also, environmental considerations such as temperature and interference from nearby electronics or electrical installations have to be factored-in because interferences from them can be sources of noise and unreliability. If these considerations are not properly executed then higher precision may actually cause more problems that it sets out to solve. Though the considerations are solvable, they come with costs-component cost, production costs, circuit complexity and labour cost. While these costs may be easily absorbed in high-end commercial developments, it goes against the focus of the current study which has as its thrust cost minimization and availability of potentiostat in low-resource and constrained budget environments.
3.3. RE Input Impedance
In the potentiostat circuit, no current is allowed to pass to the RE so as to allow the reference potential to remain unchanged during the experiment. To achieve this, the RE input impedance should be very high. The potentiostat control circuit in Figure 2 was built using ST TL084 General Purpose JFET quad operational amplifier (ST Microelectronics, Switzerland) which has an input impedance of 1012 Ohms. This imparts an impedance of 1012 on the RE input.
3.4. Ni2+/Ni(s) Reduction Reaction
Linear sweep voltammograms of Ni2+/Ni redox couple at different scan rates are presented in Figure 5. From the figure, the peak current (ip) and reduction potential (Vs. Ag/AgCl) at different scan rates were determined. These are presented in Table 1.
Since potentials were measured with respect to the Ag/AgCl reference electrode, equivalent values versus the standard hydrogen electrode (SHE) were obtained using the equation below [14] :

Figure 5. Linear sweep voltammograms of Ni2+-Ni redox couple at different scan rates.
Table 1. Peak current, diffusion coefficient and reduction potential at different scan rates.
where E (Vs SHE) is the electrode potential relative to the SHE, E (Vs reference) is the potential measured in the experiment relative to the Ag/AgCl reference and Ereference (Vs SHE) is the potential of the Ag/AgCl reference relative to the SHE. For 3 M NaCl (aq) filling solution (used in this work), Ereference (Vs SHE) is 209 mV [15] . Equivalent values of reduction potential Vs. SHE thus obtained are presented in Table 1.
It would be seen from the table that Ni2+ reduction occurs at increasingly negative potential as the scan rate increases. These values of the reduction potential of Ni2+ differ from the standard value of −0.25 V (Vs. SHE). The deposition of nickel on graphite requires high nucleation overpotential.
Nucleation overpotential of 0.3 V has been reported for the deposition of nickel on graphite [16] . Also, the electrodeposition of nickel involves a significant amount of hydrogen co-evolution [17] , and it is highly dependent on the pH. Low pH tends to favour hydrogen evolution due to the small hydrogen evolution overpotential. In a sulphate bath, electrodeposition is further inhibited by 
The relationship between the peak current and concentration of analyte’s ionic species is given by the Randles-Sevcik equation:

where ip is the peak current (in amperes), n is the number of moles of electrons appearing in half-reaction for the redox couple, ν is the scan rate at which the potential window is scanned (V/sec), F is Faraday constant (96,485 C/mol), A is the electrode’s exposed surface area (cm2), R is the Universal gas constant (8.314 J/mol K), T is the absolute temperature, and D is the analyte’s diffusion coefficient (cm2/sec).
If ambient temperature was taken to be 25˚C (298.15 K), the equation becomes:

If the concentration of the analyte (in this case, nickel sulphate), the peak current, scan rate and number of moles of electrons (n) are known, the Randles-Sevcik equation can be used to determine the diffusion coefficient of the analyte ions.
The reduction of nickel (II) ions is according to following equation:

Here n = 2. Hence using this value of n, together with other known variables in the Randles-Sevcik equation, the diffusion coefficients (D) at the different scan rates were calculated. These are presented in Table 1. The average value of D was determined to be 3.557 × 10−8 cm2/s.
The plot of peak current vs. (scan rate)1/2 is presented in Figure 6. A linear variation of peak current with the square root of the scan rate, as can be seen from the regression line through the data points, is an indication that the system follows the Randles-Sevcik equation [20] . However linearity may not indicate the reversibility of redox reaction [21] . The inability of the regression line to pass through the origin in Figure 6 indicates that the Ni2+/Ni(s) reduction is non-reversible.
The non-zero intercept can be attributed to the contribution of non-faradaic currents to the peak current [22] . At increasingly higher scan rates diffusion becomes less effective as a means of mass transport to the electrode surface.
4. Conclusion
This work has described the development steps and circuit architecture for a low-cost simplified potentiostat circuit. The microcontroller-based unit is able to demonstrate key potentiostat functionalities in the investigation of the Ni2+/Ni redox couple. The possible range of functions is expandable with expanded software algorithms. Applications for simplified potentiostat circuits transcend low-resource environments. Such simplified
Figure 6. A plot of peak current vs. square root of scan rate.
circuits can also find application in budget or low-cost monitoring and sensing instrumentation.
Cite this paper
BolajiAremo,MosobalajeOyebamiji Adeoye,Imoh BasseyObioh,Odunayo AdetolaAdeboye, (2015) A Simplified Microcontroller Based Potentiostat for Low-Resource Applications. Open Journal of Metal,05,37-46. doi: 10.4236/ojmetal.2015.54005
References
- 1. Bertocci, U. (1980) Applications of a Low Noise Potentiostat in Electrochemical Measurements. Journal of The Electrochemical Society, 127, 1931-1934.
http://dx.doi.org/10.1149/1.2130039 - 2. Blanco, J.R., Ferrero, F.J., Campo, J.C., Anton, J.C., Pingarron, J.M., Reviejo, A.J. and Manso, J. (2006) Design of Low-Cost Portable Potentiostat for Amperiometric Measurements. Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Sorrento, 24-27 April 2016, 690.
- 3. Ahmadi, M.M. and Jullien, G.A. (2005) A Very Low Power CMOS Potentiostat for Bioimplantable Applications. Proceedings of the 5th International Workshop on System-on-Chip for Real-Time Applications, Banff, 20-24 July 2005, 184.
- 4. Kelly, R.G., Yuan, J., Jones, S.H., Blanke, W., Aylor, J.H., Wan, W., Batson, A.P., Wintenbergand, A. and Clemefia, G.G. (1997) Proceedings of CORROSION 97, NACE International, Paper No. 294.
- 5. Twomey, K., Truemperand, A. and Murphy, K. (2006) A Portable Sensing System for Electronic Tongue Operations. Sensors, 6, 1679-1696.
http://dx.doi.org/10.3390/s6111679 - 6. Carminati, M., Ferrari, G., Guagliardo, F., Farina, M. and Sampietro, M. (2009) Low-Noise Single-Chip Potentiostat for Nano-Bio-Electrochemistry over a 1MHz Bandwidth. Proceedings of the 16th IEEE International Conference on Electronics, Circuits, and Systems, Yasmine Hammamet, 13-16 December 2009, 876.
- 7. Nawghare, P.M. (2009) Optimum Compensation and Stability of Potentiostat. International Journal of Electronics Engineering, 1, 1.
- 8. Smith, J. and Hinson-Smith, V. (2002) The Potentiostat: Electrochemistry’s Utility Player. Analytical Chemistry, 539A-541A.
- 9. Kubersky, P., Hamacek, A., Kroupa, M., Stulik, J. and Zwiefelhofer, V. (2012) Potentiostat Solution for Electrochemical Amperometric Gas Sensor. Proceedings of the 35th International Spring Seminar on Electronics Technology, Bad Aussee, 9-13 May 2012, 388.
- 10. Mondal, S.K., Maji, U., Tudu, B. and Koley, C. (2011) Basic Taste Identification Using Voltammetric Type Electronic Tongue Technique. International Journal of Soft Computing and Engineering, 1, 49.
- 11. Hwang, S. and Sonkusale, S. (2001) Ultra Low-Input Impedance CMOS Potentiostat for Environmental Sensing Applications. IEEE Sensors Journal, 10, 820-821.
- 12. Gopinath, A.V. and Russell, D. (2006) An Inexpensive Field Portable Programmable Potentiostat. The Chemical Educator, 11, 23-28.
- 13. Rowe, A.A., Bonham, A.J., White, R.J., Zimmer, M.P., Yadgar, R.J., Hobza, T.M., Honea, J.W., Ben-Yaacov, I. and Plaxco, K.W. (2011) CheapStat: An Open-Source, “Do-It-Yourself” Potentiostat for Analytical and Educational Applications. PLoS ONE, 6, e23783.
http://dx.doi.org/10.1371/journal.pone.0023783 - 14. Silverman, D. (2009) Reference Electrodes in Metal Corrosion. International Journal of Corrosion, 1-20.
- 15. Research Solutions & Resources LLC (2009) The Ag/AgCl Reference Electrode. Retrieved June 6, 2011, from:
http://www.consultrsr.com/resources/ref/agcl.htm - 16. Njau, K.N. and Janssen, L.J.J. (1995) Electrochemical Reduction of Nickel Ions from Dilute Solutions. Journal of Applied Electrochemistry, 25, 982-986.
http://dx.doi.org/10.1007/bf00241595 - 17. Lantelme, F., Seghiouer, A. and Derja, A. (1998) Model of Nickel Electrodeposition from Acidic Medium. Journal of Applied Electrochemistry, 28, 907-913.
http://dx.doi.org/10.1023/A:1003404118601 - 18. Grujicic, D. and Pesic, B. (2006) Electrochemical and AFM Study of Nickel Nucleation Mechanisms on Vitreous Carbon from Ammonium Sulfate Solutions. Electrochimica Acta, 51, 2678-2690.
http://dx.doi.org/10.1016/j.electacta.2005.08.017 - 19. Ningthoujam, R.S., Gajbhiye, N.S. and Sharma, S. (2009) Reduction Mechanism of Ni2+ into Ni Nanoparticles Prepared from Different Precursors: Magnetic Studies. Pramana—Journal of Physics, 72, 577-586.
http://dx.doi.org/10.1007/s12043-009-0051-6 - 20. Kumar, P.S. and Lakshminarayanan, V. (2009) Electrochemical Studies of Redox Probes in Self-Organized Lyotropic Liquid Crystalline Systems. Journal of Chemical Sciences, 121, 629-638.
http://dx.doi.org/10.1007/s12039-009-0076-x - 21. Dolati, A., Ghorbani, M. and Ahmadi, M.R. (2005) An Electrochemical Study of Au-Ni Alloy Electrodeposition from Cyanide-Citrate Electrolytes. Journal of Electroanalytical Chemistry, 577, 1-8.
http://dx.doi.org/10.1016/j.jelechem.2004.10.024 - 22. Monk, P.M.S. (2008) Fundamentals of Electroanalytical Chemistry. John Wiley & Sons, New York, 384.
NOTES
*Corresponding author.









