Open Journal of Composite Materials
Vol. 2 No. 3 (2012) , Article ID: 21295 , 16 pages DOI:10.4236/ojcm.2012.23009
Review of Recent Literature on Static Analyses of Composite Shells: 2000-2010
![]()
1School of Engineering and Technology, Central Michigan University, Mount Pleasant, USA; 2Department of Mechanical Engineering, Mississippi State University, Starkville, USA.
Email: asadi1e@cmich.edu
Received April 19th, 2012; revised May 15th, 2012; accepted May 31st, 2012
Keywords: Review; Composite; Static Analysis
ABSTRACT
Laminated composite shells are frequently used in various engineering applications including aerospace, mechanical, marine, and automotive engineering. This article reviews the recent literature on the static analysis of composite shells. It follows up with the previous work published by the first author [1-4] and it is a continuation of another recent article that focused on the dynamics of composite shells [3]. This paper reviews most of the research done in recent years (2000-2010) on the static and buckling behavior (including postbuckling) of composite shells. This review is conducted with an emphasis on the analysis performed (static, buckling, postbuckling, and others), complicating effects in both material (e.g. piezoelectric) and structure (e.g. stiffened shells), and the various shell geometries (cylindrical, conical, spherical and others). Attention is also given to the theory being applied (thin, thick, 3D, nonlinear…). However, more details regarding the theories have been described in previous work [1,3].
1. Introduction
The use of laminated composite shells in many engineering applications has been expanding rapidly in the past four decades due to their higher strength and stiffness to weight ratios when compared to most metallic materials. Composite shells now constitute a large percentage of recent aerospace or submarine structures. They are used increasingly in areas such as automotive engineering, biomedical engineering and other applications.
Literature on composite shell research can be found in many national and international conferences and journals. A recent article [3] focused on the recent research done on the dynamic behavior of composite shells wherein problems of free vibration, shock, wave propagation, dynamic stability, damping and viscoplastic behavior related to laminated shells are discussed. Several review articles on the subject, such as Qatu [2,4], Kapania [5], Noor and Burton [6,7], Noor et al. [8], and Soldatos [9] covered much of the research done in past decades. Computational aspects of the research were covered by Noor and Burton [6,7], Noor et al. [8,10] and Noor and Venneri [11]. Carrera [12] presented a historical review of zigzag theories for multilayered plates and shells. He also reviewed the theories and finite elements for multilayered, anisotropic, composite plates and shells [13]. Among the recent books on the subject are those by Reddy [14], Ye [15], Lee [16], and Shen [17].
Present article reviews only recent research (2000 through 2010) done on the static and buckling analyses of composite shells. It includes stress, deformation, buckling and post buckling analyses under mechanical, thermal, hygrothermal or electrical loading. Since there are extensive papers on experimental and optimization studies in literature, those topics have not been discussed in this review separately. However, papers in those topics based on their obtained results are classified in the topics of this review.
This article classifies research based upon the typically used shell theories. These include thin (or classical) and thick shell theories (including shear deformation and three dimensional theories), shallow and deep theories, linear and nonlinear theories, and others. Most theories are classified based on the thickness ratio of the shell being treated (defined as the ratio of the thickness of the shell to the shortest of the span lengths and/or radii of curvature), its shallowness ratio (defined as the ratio of the shortest span length to one of the radii of curvature) and the magnitude of deformation (compared mainly to its thickness). Fundamental equations are listed for the types of shells used by most researchers in other publications [1-4].
The literature is reviewed while focusing on various aspects of research. Focus will first be placed on the various shell geometries that are receiving attention in recent years. Among classical shell geometries are the cylindrical, spherical, conical shells and other shells of revolution; other shells like shallow shells are also included in this review. Stress and deformation analyses, in which various boundary conditions and/or shell geometries are considered, buckling and post-buckling problems, and finally research dealing with thermal and/or hygrothermal environments will be reviewed. The third aspect of research will focus on material-related complexities, which include piezoelectric or other complex materials. Structural-related complexities will be the final category that will be addressed. This will include stiffened shells, shells with cut-outs, shells with imperfections or other complexities.
2. Shell Theories
Shells are three dimensional bodies bounded by two, relatively close, curved surfaces. The three dimensional equations of elasticity are complicated when written in curvilinear, or shell, coordinates. Researchers simplify such shell equations by making certain assumptions for particular applications. Almost all shell theories (thin and thick, deep and shallow …) reduce the three-dimensional (3D) elasticity problem into a two dimensional (2D) problem. The accuracy of thin and thick shell theories is established when their results are compared to those of 3D theory of elasticity.
2.1. Three Dimensional Elasticity Theory
A shell is a three dimensional body confined by two parallel (unless the thickness is varying) surfaces. In general, the distance between those surfaces is small compared with other shell parameters. In this section, the equations from the theory of 3D elasticity in curvilinear coordinates are presented. The literature regarding Mechanics of laminated shells using 3D elasticity theory will then be reviewed.
Consider a shell element of thickness h, radii of curvature Ra and Rb (a radius of twist Rab is not shown here) (Figure 1). Assume that the deformation of the shell is small compared to the shell dimensions. This assumption allows us to neglect nonlinear terms in the subsequent derivation. It will also allow us to refer the analysis to the original configuration of the shell. The strain displacement relations can be written as [1]
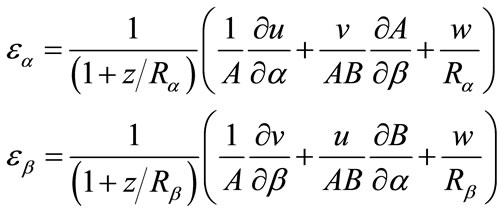
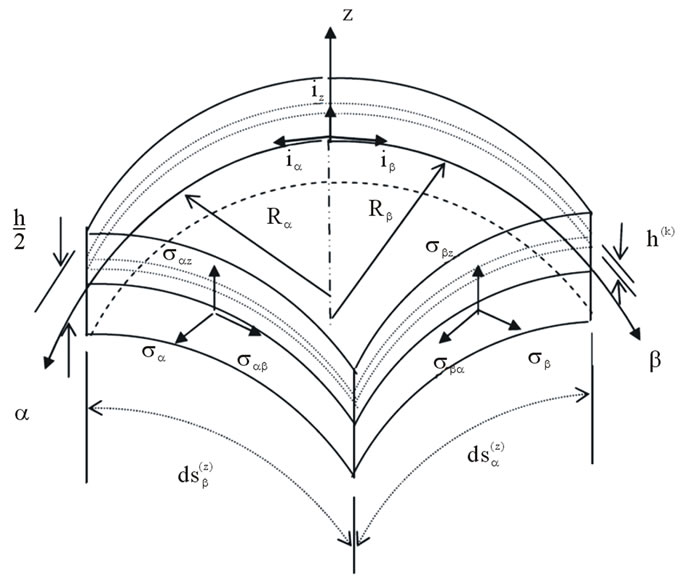
Figure 1. Stresses in shell coordinates (free outer surfaces).
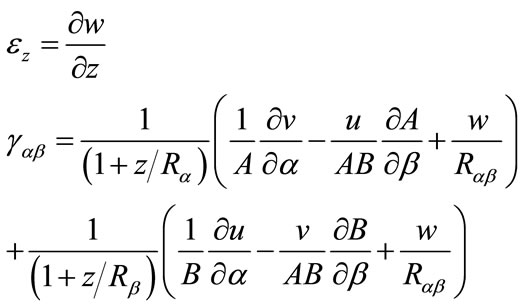
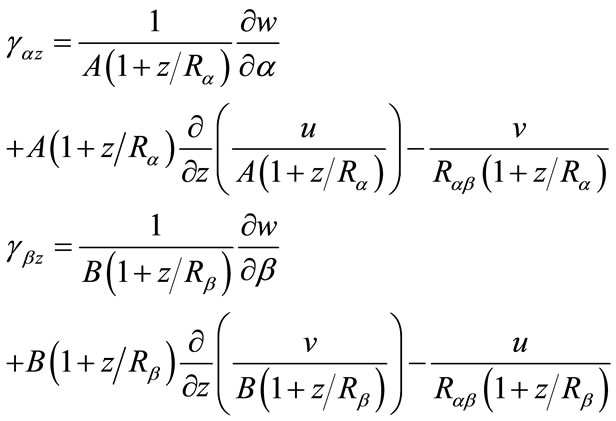 (1)
(1)
The laminated composite shells are assumed to be composed of plies of unidirectional long fibers embedded in a matrix material. On a macroscopic level, each layer may be regarded as being homogeneous and orthotropic. However, the fibers of a typical layer may not be parallel to the coordinates in which the shell equations are expressed. The stress-strain relationship for a typical nth lamina in a laminated composite shell made of N laminas as shown in Figure 2 is given by Equation (2) [1].
 (2)
(2)
Figure 2. Lamination parameters in shells.
The positive notations of the stresses are shown in Figure 1.
In order to develop a consistent set of equations, the boundary conditions and the equilibrium equations will be derived using the principle of virtual work, which yields the following equilibrium equations
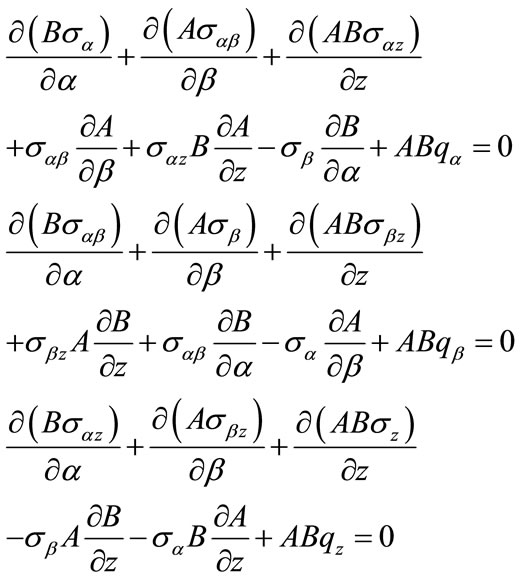 (3)
(3)
The principle of virtual work will also yield boundary terms that are consistent with the other equations. The boundary terms for z = constant are:
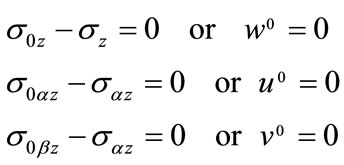 (4)
(4)
where s0z , s0az and s0bz are surface tractions and u0, v0 and w0 are displacement functions at z = constant. Similar results are obtained for the boundaries a = constant and b = constant. A three dimensional shell element has six surfaces. With three equations at each surface, a total of 18 equations can be obtained for a single-layered shell.
The above equations are valid for single-layered shells. To use 3D elasticity theory for multi-layered shells, each layer must be treated as an individual shell. Both displacements and stresses must be continuous between each layer (layer k to layer k + 1) in a n-ply laminate to insure that there are no free internal surfaces (i.e., delamination) between the layers.
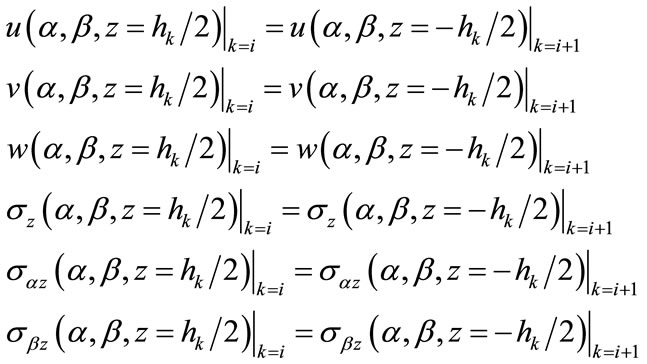 (5)
(5)
For k = 1,···, N – 1.
Among the recent work that used 3D theory of elasticity is the work of Sheng and Ye [18] who presented a 3D state space finite element solution for composite cylindrical shells. Wu and Lo [19] discussed 3D elasticity solutions of laminated annular spherical shells. Wang and Zhong [20] used 3D theory to solve problems with smart laminated anisotropic circular cylindrical shells with imperfect bonding. Li and Shen [21] studied postbuckling of 3D textile composite cylindrical shells under axial compression in thermal environments. Santos et al. [22,23] showed a finite element model for the analysis of 3D axisymmetric laminated shells with piezoelectric sensors and actuators. Sprenger et al. [24] investigated delamination growth in laminated structures with 3D-shell elements and a viscoplastic softening model. Li and Shen [25,26] analyzed postbuckling of 3D braided composite cylindrical shells under various loading in thermal environments. Alibeigloo and Nouri [27] found a three-dimensional solution for static analysis of functionally graded (FG) cylindrical shells with bonded piezoelectric layers by utilizing differential quadrature method (DQM) to the edge boundary conditions and in-plane differentials and using state-space approach for discrete points. Fagiano et al. [28] used 3-D finite element method to accurately predict interlaminar stresses for multilayer composite shells. Nosier and Ruhi [29] found an exact solution for a laminated piezoelectric finite panels under static electro mechanical loading. They reduced PDEs of equilibrium equations to a system of ODEs using trigonometric functions for displacements in longitudinal and circumferential directions, and then they solved the resulted system of ODEs. The similar procedure followed by Ruhi et al. [30] to find the solution of a functionally graded cylinder under thermoelastic loading.
2.2. Thick Shell Theory
Thick shells are defined as shells with a thickness smaller by at least one order of magnitude when compared with other shell parameters such as wavelength and/or radii of curvature (thickness is at least 1/10 of the smaller length of the shell). The main differentiation between thick shell and thin shell theories is the inclusion of shear deformation and rotary inertia effects. Theories that include shear deformation are referred to as thick shell theories or shear deformation theories.
Thick shell theories are typically based on either a displacement or stress approach. In the former, the midplane shell displacements are expanded in terms of shell thickness, which can be a first order expansion, referred to as first order shear deformation theories.
The 3D elasticity theory is reduced to a 2D theory using the assumption that the normal strains acting upon the plane parallel to the middle surface are negligible compared with other strain components. This assumption is generally valid except within the vicinity of a highly concentrated force (St. Venant’s principle). In other words, no stretching is assumed in the z-direction (i.e., ez = 0). Assuming that normals to the midsurface strains remain straight during deformation but not normal, the displacements can be written as [1]
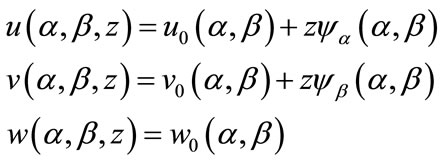 (6)
(6)
where u0, v0 and w0 are midsurface displacements of the shell and ya and yb are midsurface rotations. An alternative derivation can be made with the assumption sz = 0. The subscript (0) will refer to the middle surface in subsequent equations. The above equations describe a typical first-order shear deformation shell theory, and will constitute the only assumption made in this analysis when compared with the 3D theory of elasticity. As a result, strains are written as [1]
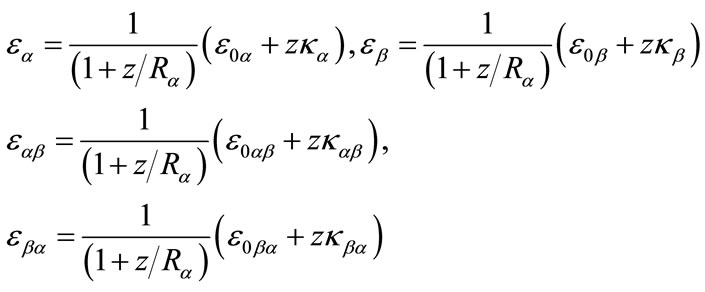
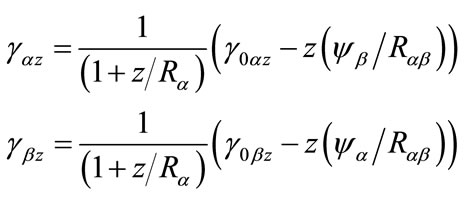 (7)
(7)
where the midsurface strains are:
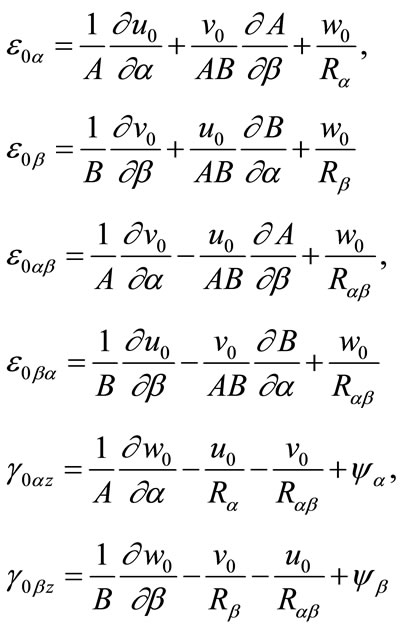 (8a)
(8a)
and the curvature and twist changes are:
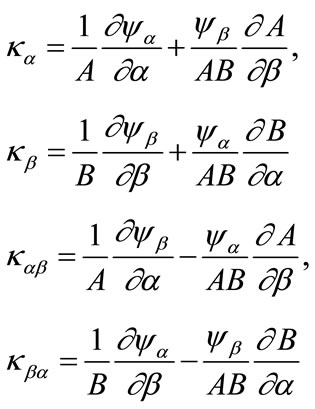 (8b)
(8b)
The force and moment resultants (Figures 3 and 4) are obtained by integrating the stresses over the shell thickness considering the (1 + ) term that appears in the denominator of the stress resultant equations [5]. The stress resultant equations are:
) term that appears in the denominator of the stress resultant equations [5]. The stress resultant equations are:
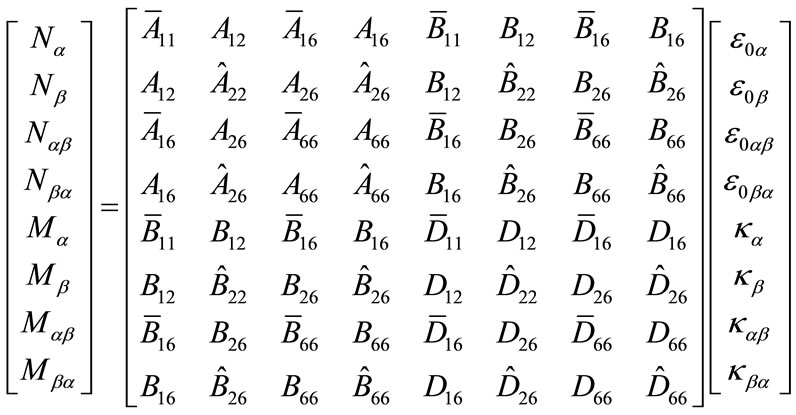 (9)
(9)
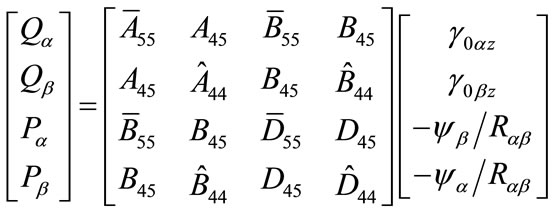 (10)
(10)
where 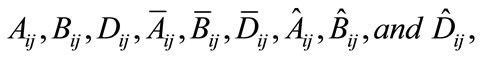 are defined in [1].
are defined in [1].
It has been shown [1,5] that the above Equations (9) and (10) yield more accurate results when compared with those of plates and those traditionally used for shells [18]. Priciple of virtual work can be used to derive the consistent equilibrium equations and boundary conditions. The equilibrium equations are [1-4]:
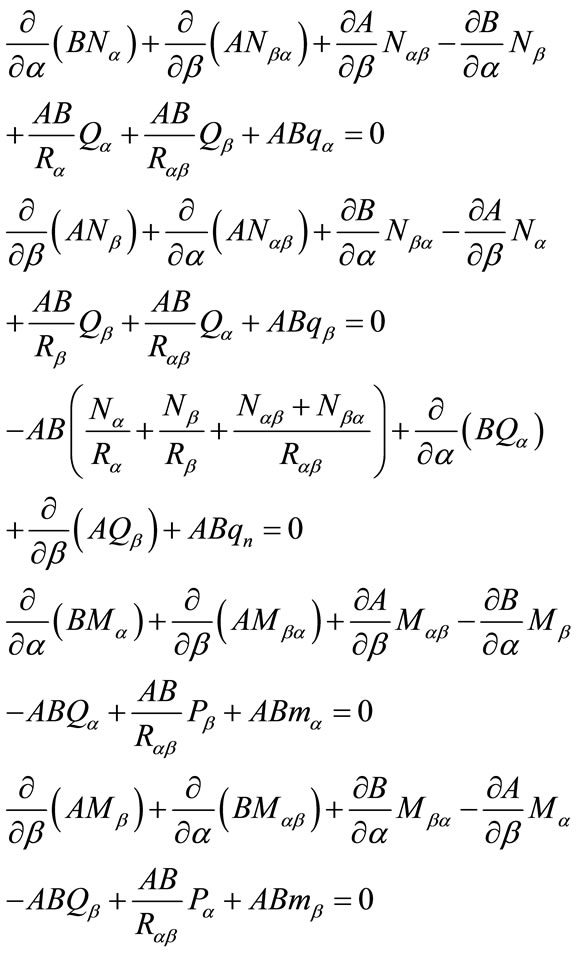 (11)
(11)
The boundary terms for the boundaries with a = constant are
 (12)
(12)
Similar equations can be obtained for b = constant.
Equations (9) and (10) are significantly different from those that cover most of first order shear deformation theories (FSDTs) for shells which neglect the effect of  in the stress resultant equations. Asadi et al. [31]
in the stress resultant equations. Asadi et al. [31]

Figure 3. Force resultants in shell coordinates.
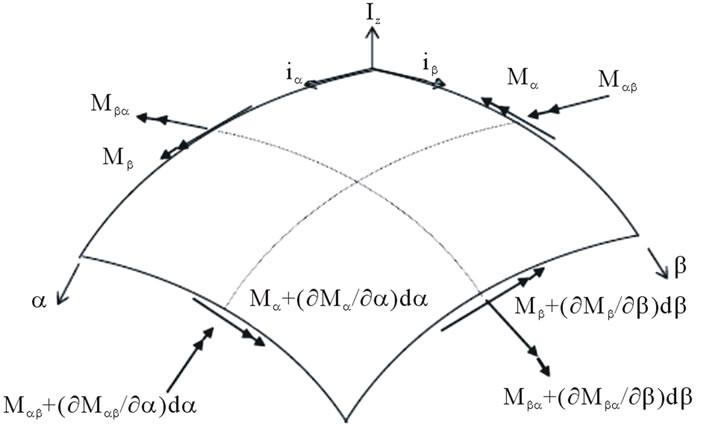
Figure 4. Moment resultants in shell coordinates.
studied static and free vibration of composite shells using Equations (9) and (10) and compared their results with other FSDTs and 3D elasticity results. They showed that presented FSDT improves the prediction of displacements, force resultants and moment resultants signifycantly.
Shear deformation theories were used by many authors (e.g. Qatu [4]). Chaudhuri [32] presented a nonlinear zigzag theory for finite element analysis of shear-deformable laminated shells. Krejaa and Schmidt [33] studied large rotations in shear deformation finite element analysis of laminated shells. Non-linear buckling and postbuckling of a moderately thick anisotropic laminated cylindrical shell of finite length subjected to lateral pressure, hydrostatic pressure and external liquid pressure based on a higher order shear deformation shell theory with von Kármán-Donnell-type of kinematic nonlinearity and including the extension/twist, extension/ flexural and flexural/twist couplings were presented by Li and Lin [34] wherein the material property of each layer could be linearly elastic, anisotropic and fiber-reinforced. A mixed meshless computational method based on the Local Petrov-Galerkin approach for analysis of plate and shell structures was presented by Sorić and Jarak [35]. They overcame the undesired locking phenomena and demonstrated that this meshless method is numerically more efficient than the available meshless fully displacement approaches. Shen [36,37] investigated postbuckling of shear deformable cross-ply laminated cylindrical shells under combined loading.
Piskunov et al. [38] were interested in a ratational higher order shear deformation theory of anisotropic laminated plates and shells. Iozzi and Gaudenzi [39] studied shear deformable shell elements for adaptive laminated structures. Han et al. [40] performed a geometrically nonlinear analysis of laminated composite thin shells using a modified first-order shear deformable element. Other studies that used a shear deformation shell theory include those of Li [41], Zenkour [42], Shen [43], Shen and Li [44], Balah and Al-Ghamedy [45], and Ferriera [46].
Zhen and Wanji [47] presented a higher order theory for multilayered shells and performed analysis on laminated cylindrical shell panels. Khare et al. [48] discussed closed-form thermo-mechanical solutions of higher-order theories of cross-ply laminated shallow shells. Khare and Rode [49] showed similar solutions for thick laminated sandwich shells. Ferreira et al. [50] modeled cross-ply laminated elastic shells by a higher-order theory. Alijani and Aghdam [51] presented a semi-analytical solution for stress analysis of moderately thick laminated cylindrical panels with various boundary conditions. Pinto Correia et al. [52] analyzed laminated conical shell structures for buckling using higher order models. Matsunaga [53] studied thermal buckling of cross-ply laminated composite shallow shells according to a higher order deformation theory. Oh and Cho [54] investigated a higher order zigzag theory for smart composite shells under mechanical-thermo-electric loading. Yaghoubshahi et al. [55] and Asadi and Faribrz [56] employed general higher-order shear deformation theory and formulated it to analyze deep composite shells and plates with mixed boundary conditions. Benson et al. [57] presented a ReissnerMindlin shell formulation based on a degenerated solid is implemented for NURBS-based isogeometric analysis. They constructed a user-defined element in LS-Dyna for industrial purposes to analyze elasto-plastic behavior of shells.
In general, layer-wise laminate theories are used to properly represent local effects, such as interlaminar stress distribution, delaminations, etc. These theories are typically employed for cases involving anisotropic materials in which transverse shear effects cannot be ignored. Recent studies include Yuan et al. [58] in which a stress projection, layer-wise-equivalent formulation was used for accurate predictions of transverse stresses in laminated plates and shells. Kim and Chaudhuri [59,60] and Chaudhuri and Kim [61] described a layer-wise linear displacement distribution theory and based their analysis on it to investigate the buckling and shear behavior of a long cross-ply cylindrical shell (ring). Leigh and Tafreshi [62] used layerwise shell finite element based on first order shear deformation theory to investigate delamination buckling of composite cylindrical shells. A static analysis of thick composite circular arches using a layerwise differential quadrature technique was performed by Malekzadeh [63]. Roh et al. [64,65] investigated the thermo-mechanical behavior of shape memory alloys using a finite element method based on layerwise theory. The theory of layerwise displacement field was used to perform a finite element analysis of aero-thermally buckled composite shells by Shin et al. [66]. The displacement field of a layerwise theory was also used to develop laminated beam theories by Tahani [67].
2.3. Thin Shell Theory
If the shell thickness is less than 1/20 of the other shell dimensions (e.g. length) and/or radii of curvature, a thin shell theory, where shear deformation and rotary inertia are negligible, is generally acceptable. Depending on various assumptions made during the derivation of the strain-displacement relations, stress-strain relations, and the equilibrium equations, various thin shell theories can be derived [5]. All these theories were initially derived for isotropic shells and expanded later for laminated composite shells by applying the appropriate integration through laminas, and stress-strain relations. For very thin shells, the shell is thin such that the ratio of the thickness compared to any of the shell’s radii or any other shell parameter, i.e., width or length, is negligible when compared to unity. Also, for thin shells, the normals to the middle surface remain straight and normal when the shell undergoes deformation. This assumption assures that certain parameters in the shell equations (including the  term mentioned earlier in the thick shell theory) can be neglected. The shear deformation can be neglected in the kinematic equations allowing the in-plane displacement to vary linearly through the shell’s thickness as given by
term mentioned earlier in the thick shell theory) can be neglected. The shear deformation can be neglected in the kinematic equations allowing the in-plane displacement to vary linearly through the shell’s thickness as given by
 (13)
(13)
where the midsurface strains, curvature and twist changes are
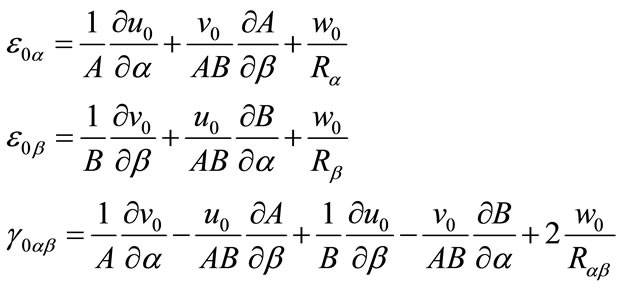 (14a)
(14a)
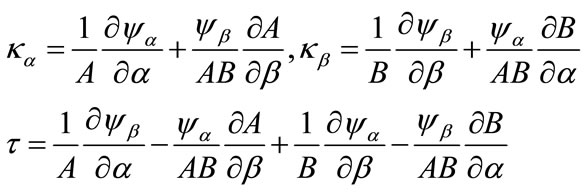 (14b)
(14b)
and where
 . (14c)
. (14c)
Applying Kirchhoff hypothesis of neglecting shear deformation and the assumption that ez is negligible, the stress-strain equations for an element of material in the kth lamina may be written as [1]
 (15)
(15)
where sa and sb are normal stress components, tab is the in-plane shear stress component [1], ea and eb are the normal strains, and gab is the in-plane engineering shear strain. The terms Qij are the elastic stiffness coefficients for the material. If the shell coordinates (a,b) are parallel or perpendicular to the fibers, then the terms Q16 and Q26 are both zero. Stresses over the shell thickness (h) are integrated to get the force and moment resultants as given by
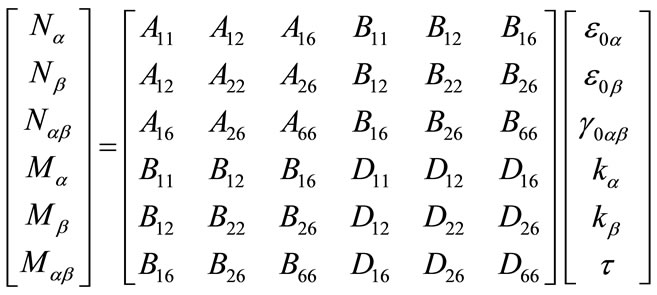 (16)
(16)
where Aij, Bij, and Dij are the stiffness coefficients arising from the piecewise integration over the shell thickness (Equation (14b)). For shells which are laminated symmetrically with respect to their midsurfaces, all the Bij terms become zero. Note that the above equations are the same as those for laminated plates, which are also valid for thin laminated shells. Using principle of virtual work yields the following equilibrium equations.
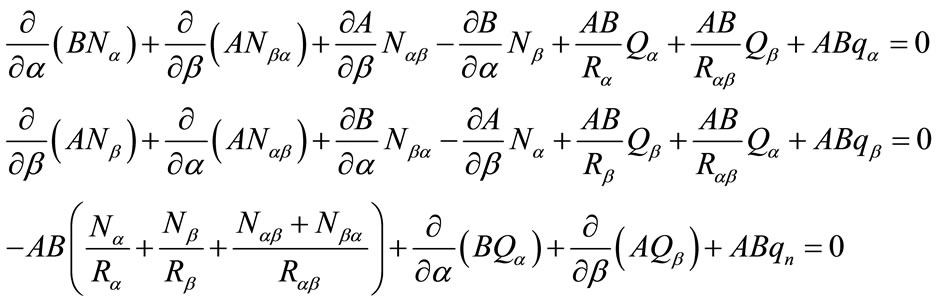
where
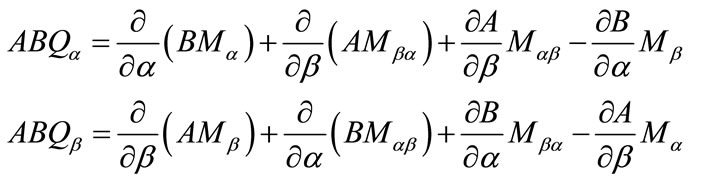 (17)
(17)
The following boundary conditions can be obtained for thin shells for a = constant (similar equations can be obtained for b = constant).
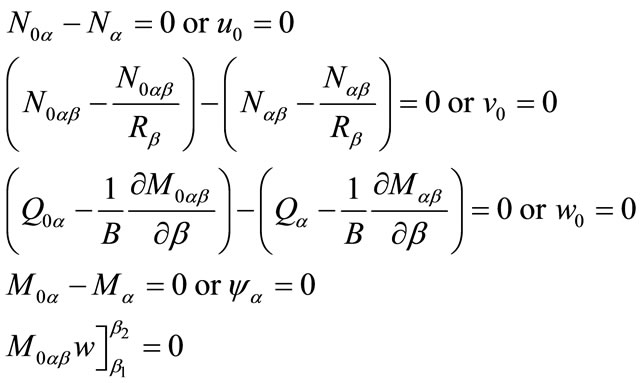 (18)
(18)
where 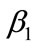 and
and 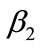 are, respectively, the start and end points of the shell in
are, respectively, the start and end points of the shell in  direction. Qatu and Asadi [68] used the formulation in this section and simplified it to analyze different type of shells including cylindrical, spherical and paraboloidal shells. However, they did not give numerical examples for static analysis of different shells. Shen [69] studied buckling and postbuckling of laminated thin cylindrical shells under hygrothermal environments. Soldatos and Shu [70] discussed modeling of perfectly and weakly bonded laminated plates and shallow shells. Chaudhuri et al. [71] presented admissible boundary conditions and solutions to internally pressurized thin cylindrical shells. Khosravi et al. [72] illustrated a shell element for co-rotational nonlinear analysis of thin and moderately thick laminated structures. Sofiyev et al. [73] discussed buckling of laminated cylindrical thin shells under torsion. Weicker et al. [74,75] in two companion papers derived governing equilibrium conditions for a thin-walled pipe subjected to general loading based on thin shell theory and found exact and finite element solutions and compared them with each others. Kiendla et al. [76] proposed an isogeometric formulation for rotation-free thin shell analysis of structures comprised of multiple patches and applied that to real wind turbine problems. Prabu et al. [77] performed a parametric study on buckling behavior of dented short carbon steel cylindrical thin shell subjected to uniform axial compression by non-linear static buckling analysis. The elastic modulus reduction method (EMRM) was proposed by Yu and Yang [78] to calculate lower-bound limit loads of thin plate and shell structures. Challagulla et al. [79] performed micromechanical analysis of gridreinforced thin composite shells. Stress, deformation and stability conditions for thin doubly curved shallow bimetallic shells taking large displacements under homogenous thermal field to account were done by Jakomina et al. [80]. Ghassemi et al. [81] employed a finite element model in order to analyze large displacements. Since, the finite-element implementation for this kind of problems suffers from membrane and shear locking, especially for very thin shells, the mid-surface of the shell is regarded as a Cosserat surface with one inextensible director to overcome these numerical problems. Other studies include those of Morozov [82], Guz’ and Shnerenko [83], and Maksimyuk and Chernyshenko [84].
direction. Qatu and Asadi [68] used the formulation in this section and simplified it to analyze different type of shells including cylindrical, spherical and paraboloidal shells. However, they did not give numerical examples for static analysis of different shells. Shen [69] studied buckling and postbuckling of laminated thin cylindrical shells under hygrothermal environments. Soldatos and Shu [70] discussed modeling of perfectly and weakly bonded laminated plates and shallow shells. Chaudhuri et al. [71] presented admissible boundary conditions and solutions to internally pressurized thin cylindrical shells. Khosravi et al. [72] illustrated a shell element for co-rotational nonlinear analysis of thin and moderately thick laminated structures. Sofiyev et al. [73] discussed buckling of laminated cylindrical thin shells under torsion. Weicker et al. [74,75] in two companion papers derived governing equilibrium conditions for a thin-walled pipe subjected to general loading based on thin shell theory and found exact and finite element solutions and compared them with each others. Kiendla et al. [76] proposed an isogeometric formulation for rotation-free thin shell analysis of structures comprised of multiple patches and applied that to real wind turbine problems. Prabu et al. [77] performed a parametric study on buckling behavior of dented short carbon steel cylindrical thin shell subjected to uniform axial compression by non-linear static buckling analysis. The elastic modulus reduction method (EMRM) was proposed by Yu and Yang [78] to calculate lower-bound limit loads of thin plate and shell structures. Challagulla et al. [79] performed micromechanical analysis of gridreinforced thin composite shells. Stress, deformation and stability conditions for thin doubly curved shallow bimetallic shells taking large displacements under homogenous thermal field to account were done by Jakomina et al. [80]. Ghassemi et al. [81] employed a finite element model in order to analyze large displacements. Since, the finite-element implementation for this kind of problems suffers from membrane and shear locking, especially for very thin shells, the mid-surface of the shell is regarded as a Cosserat surface with one inextensible director to overcome these numerical problems. Other studies include those of Morozov [82], Guz’ and Shnerenko [83], and Maksimyuk and Chernyshenko [84].
2.4. Nonlinear Theories
The magnitude of transverse displacement compared to shell thickness is the third criterion used in classifying shell equations. In many cases, nonlinear terms in the fundamental shell equations are expanded using perturbbation methods, and smaller orders of the rotations are retained. Most frequently, the first order only is retained and occasionally third orders have been included in nonlinear shell theories. In some shell problems, the material used can also be nonlinear (e.g., rubber, plastics and others). Theories that include materials nonlinearity are also referred to as nonlinear shell theories as well. The vast majority of shell theories, however, deal with geometric nonlinearity only.
Galishin and Shevchenko [85] determined the axisymmetric nonlinear thermoelastoplastic state of laminated orthotropic shells. Wang et al. [86] studied the nonlinear dynamic response and buckling of laminated cylindrical shells with axial shallow grooves. Nonlinear finite element analyses were performed by Kundu et al. [87], Naidu and Sinha [88] and Guo et al. [89]. Patel et al. [90,91] investigated nonlinear thermo-elastic buckling characteristics of cross-ply laminated joined conical and cylindrical shells. Xu et al. [92] studied nonlinear stability of double-deck reticulated circular shallow spherical shell based on the variational equation of the nonlinear bending theory. Panda and Singh [93] studied thermal buckling and post-buckling analysis of a laminated composite spherical shell panel embedded with shape memory alloy fibers using nonlinear finite element methods. Sze and Zheng [94] studied a hybrid-stress solid element for geometrically nonlinear laminated shell analyses. Andrade et al. [95] and Kima et al. [96] performed geometrically nonlinear analysis of laminated composite plates and shells using various shell elements. Huang [97] performed nonlinear buckling of composite shells of revolution. Ferreira et al. [98] conducted a nonlinear finite element analysis of rubber composite shells. Material nonlinearity was discussed by Khoroshun et al. [99,100].
Other nonlinear analyses include Chaudhuri [32], Khosravi et al. [72], Han et al. [40], Hsia [101], Wang et al. [102], Moitaa et al. [103], Jakomina et al. [80], Li and Lin [34], and Razzaq and El-Zafrany [104].
2.5. Shell Geometries
Shells may have different geometries based mainly on their curvature characteristics. In most shell geometries, the fundamental equations have to be treated at a very basic level. The equations are affected by the choice of the coordinate system, the characteristics of the Lame parameters and curvature [1-4]. Equations for cylindrical, spherical, conical and barrel shells can be derived from the equations of the more general case of shells of revolution. Equations for cylindrical, barrel, twisted and shallow shells can also be derived from the general equations of doubly curved shells. Cylindrical shells, doubly curved shallow shells, spherical and conical shells are the most treated geometries in research.
Bespalova and Urusova [105] studied contact interacttion between prestressed laminated shells of revolution and a flat foundation. Pinto Correia et al. [106] investigated modeling and optimization of laminated adaptive shells of revolution. Vasilenko et al. [107] described contact interaction between a laminated shell of revolution and a rigid or elastic foundation. Khoroshun and Babich [108] discussed stability of laminated convex shells of revolution with micro-damages in laminate components. Vasilenko et al. [109] analyzed stresses in laminated shells of revolution with an imperfect interlayer contact. Gureeva et al. [110] analyzed an arbitrary loaded shell of revolution based on the finite element method in a mixed formulation. Merzlyakov and Galishin [111] investigated thermoelastoplastic non-axisymmetric stress-strain analysis of laminated shells of revolution. Ye and Zhou [112] analyzed the bending of composite shallow shells of revolution. Stability of composite shells of revolution was picked up by Trach [113] and Khoroshun and Babich [114].
Shin et al. [115] investigated thermal post-buckled behaviors of cylindrical composite shells with viscoelastic damping treatments. Bhaskar and Balasubramanyam [116] showed accurate analysis of end-loaded laminated orthotropic cylindrical shells. Merglyakov and Gatishin [117] performed analysis of the thermoelastoplastic nonaxisymmetric laminated circular cylindrical shells. Weaver et al. [118] investigated anisotropic effects in the compression buckling of laminated cylindrical shells. Huang and Lu [119], Shen and Xiang [120] studied buckling and postbuckling of cylindrical shells under combined compression and torsion. Diaconu et al. [121] studied buckling characteristics and layup optimization of long laminated composite cylindrical shells subjected to combined loads. Fu and Yang [122] and Yang and Fu [123] described delamination growth for composite laminated cylindrical shells under external pressure. Shen [124] conducted a study on the hygrothermal effects on the postbuckling of laminated cylindrical shells. Wang and Dong [125] were interested in local buckling for triangular delaminations near the surface of laminated cylindrical shells under hygrothermal effects. Goldfeld and Ejgenberg [126] were interested in linear bifurcation analysis of laminated cylindrical shells. Shen [127,128] and Shen and Li [129] analyzed postbuckling of axially-loaded laminated cylindrical shells with piezoelectric actuators. Panda and Ramachandra [130] studied postbuckling analysis of cross-ply laminated cylindrical shell panels under parabolic mechanical edge loading. Rahman and Jansen [131] presented a finite element formulation of Koiter’s initial post-buckling theory using a multi-mode approach for coupled mode initial postbuckling analysis of a composite cylindrical shell.
Studies on buckling of cylindrical shells include Wangi and Xiao [132], Shen [133-135], Wang et al. [136], Geier et al. [137], Weaver et al. [138], Wang and Dai [139], Zhu et al. [140], Patel et al. [141], Yang and Fu [142], Hilburger and Starnes [143], Semenyuk et al. [144], Tafreshi [145], Solaimurugan and Velmurugan [146], Semenyuk and Zhukova [147], Tafreshi [148], Weaver and Dickenson [149], Kere and Lyly [150], Vaziri [151], Semenyuk et al. [152], Tafreshi [153,154], Babich and Semenyuk [155], Biagi and Medico [156], Sheinman and Jabareen [157], Prabu et al. [77], Li and Lin [34], and De Faria [158].
Wang et al. [159] presented a method for interlaminar stress analysis in a laminated cylindrical shell. Lin and Jen [160] performed analysis of laminated anisotropic cylindrical shell by Chebyshev collocation method. Lemanski and Weaver [161] were interested in optimization of a 4-layer laminated cylindrical shell. Gong and LingFeng [162] did experimental study and numerical calculation of stability and load-carrying capacity of cylindrical shell with initial dent. Khoroshun and Babich [163] investigated stability of cylindrical shells with damageable components. Alibeigloo [164] performed a static analysis of an anisotropic laminated cylindrical shell with piezoelectric layers. Goldfeld [165] studied the influence of the stiffness coefficients on the imperfection sensitiveity of laminated cylindrical shells. Zenkour and Fares [166] picked up the problem of thermal bending analysis of composite laminated cylindrical shells. Jinhua et al. [167] performed variational analysis of delamination growth for composite laminated cylindrical shells under concentrated load. Meink et al. [168] studied filament wound composite cylindrical shells. Solaimurugan and Velmurugan [169] researched progressive crushing of stitched glass-polyester composite cylindrical shells.
Other analyses include those of Sheng and Ye [18], Li and Shen [21,25,26], Shen [36,37], Li [41], Zenkour [42], Shen and Li [44], Zen and Wanji [47], Chaudhuri et al. [71], Sofiyev et al. [73], Patel et al. [90], Khoroshun et al. [99,100], Wang et al. [102], Zhu et al. [140], Seif et al. [170], Burgueño and Bhide [171], Belozerov and Kireev [172], Alibeigloo and Nouri. [27], Semenyuk and Trach [173], Paris and Costello [174] and Movsumov and Shamiev [175]. As can be seen from the above review, cylindrical shells received the most attention (as compared with other shell geometries.
Khare et al. [48] presented closed-form thermo-mechanical solutions of cross-ply laminated shallow shells. Soldatos and Shu [70] discussed modeling of perfectly and weakly bonded laminated plates and shallow shells. Zang et al. [176] were interested in nonlinear dynamic buckling of laminated shallow spherical shells. Kioua and Mirza [177] investigated piezoelectric induced bending and twisting of laminated shallow shells. Niemi [178] developed a four-node bilinear shell element of arbitrary quadrilateral shape and applied that to find the solution of static and vibration problems of shallow shells. Zarivnyak [179] researched the probability of the critical state of glue joints of a shallow laminated shell. Other studies on shallow shells include those of Grigorenko et al. [180] Matsunaga [53], Wang et al. [86], Ye and Zhou [112], Jakomina et al. [80], Xu et al. [92], Gupta [181], and Zhu et al. [140].
Conical shells are other special cases of shells of revolution. For these shells, a straight line revolves about an axis to generate the surface. Wu et al. [182] discussed a refined asymptotic theory of laminated circular conical shells. Das and Chakravorty [183] suggested selection guidelines of point-supported composite conoidal shell roofs based on a finite element analysis. Mahdi et al. [184] investigated the effect of material and geometry on crushing behavior of laminated conical shells. Goldfeld [185] studied the imperfection sensitivity of laminated conical shells. Goldfeld et al. [186] performed a multifidelity optimization of laminated conical shells for buckling. Mahdi et al. [187] were interested in the effect of residual stresses in a filament wound laminated conical shell. Singh and Babu [188] studied thermal buckling of laminated piezoelectric conical shells. Wu and Chiu [189] picked up the problem of thermoelastic buckling of laminated conical shells. Rezadoust et al. [190] investigated the crush behavior of conical composite shells. Goldfeld et al. [191] presented design and optimization of laminated conical shells for buckling. Kosonen [192] described specification for mechanical analysis of conical composite shells. Other studies on conical include Patel et al. [90,193,194], and Pinto Correia [52].
Spherical shells are other special cases of shells of revolution. For these shells, a circular arc, rather than a straight line, revolves about an axis to generate the surface. If the circular arc is half a circle and the axis of rotation is the circle’s own diameter, a closed sphere will result. Smithmaitrie and Tzou [195] discussed actions of actuator patches laminated on hemispherical shells. Marchuk and Khomyak [196] presented refined mixed finite element solutions of laminated spherical shells. He and Hwang [197] investigated identifying damage in spherecal laminated shells. Kadoli and Ganesan [198] analyzed thermoelastic buckling of composite hemispherical shells with a cut-out at the apex. Saleh et al. [199] described crushing behavior of composite hemispherical shells subjected to axial compressive load. Other studies on spherical shells include those of Zang et al. [176], Wu and Lo [19], Xu et al. [92], Panda and Singh [93], and others.
Tzou et al. [200] studied sensitivity of actuator patches laminated on toroidal shells. Mitkevich and Kul’kov [201] investigated design optimization and forming methods for toroidal composite shells.
Sai et al. [202,203] investigated shells with and without cut-outs. Other study includes Latifa and Sinha [204].
3. Types of Analyses
Analyses can be dynamic in nature. These include free and transient vibrations, wave propagation, dynamic stability, shock and impact loadings and others. These were covered in another review article [3]. The types of analyses that this work focuses on are static, buckling, post buckling, thermal and hygrothermal, and failure and damage.
3.1. Static Analysis
Pinto Correiaa et al. [205] described a finite element semi-analytical model for laminated axisymmetric shells under static and other loads. Prusty [206] performed linear static analysis of composite hat-stiffened laminated shells using finite elements. Park et al. [207] analyzed laminated composite plates and shells using a shell element. Alijani et al. [208] studied application of the extended Kantorovich method to the bending of clamped cylindrical panels. Santos et al. [23] presented a finite element bending analysis of 3D axisymmetric laminated piezoelectric shells. Babeshko and Shevchenko [209- 211], Babeshko [212] and Shevchenko and Babeshko [213,214] discussed elastoplastic laminated shells made of isotropic, transversely isotropic and laminated materials. Maslov et al. [215] presented a method of stressed state analysis of thick-walled composite shells. Abouhamze et al. [216] studied Bending of symmetrically laminated cylindrical panels using the extended Kantorovich method.
Other static analyses include Alibeigloo and Nouri [27], Yuan et al. [58], Maksimyuk and Chernyshenko [84], Razzaq and El-Zafrany [104], Vasilenko et al. [109], Ye and Zhou [112], Tafreshi [145], Wang et al. [159], Alibeigloo [164], Zenkour and Fares [166], Seif et al. [170], Semenyuk and Trach [173], Paris and Costello [174], Kioua and Mirza [177], Grigorenko et al. [180], Mahdi et al. [187], Marchuk and Khomyak [196], Saleh et al. [199], and Sai Ram and Sreedhar Batu [202,203].
3.2. Buckling Analysis
Lee and Lee [217] discussed a numerical analysis of the buckling and postbuckling behavior of laminated composite shells. Sai-Ram et al. [218] studied buckling of laminated composite shells under transverse load. Fan et al. [219] investigated creep buckling of viscoelastic laminated plates and circular cylindrical shells. Li et al. [220] performed buckling analysis of rotationally periodic laminated composite shells by finite elements. Sofiyev [221] conducted torsional buckling analysis of crossply laminated orthotropic composite cylindrical shells. Patel et al. [222] were interested in thermo-elastic buckling of angle-ply laminated elliptical cylindrical shells. Hilburger and Starnes [223] studied the effects of imperfections of the buckling response of composite shells. Rickards et al. [224] analyzed buckling of composite stiffened shells.
Studies on buckling of cylindrical shells include Wangi and Xiao [132], Shen [133-135], Wang et al. [136], Geier et al. [137], Weaver et al. [138], Wang and Dai [139], Zhu et al. [140], Patel et al. [141], Yang and Fu [142], Hilburger and Starnes [143], Semenyuk [144], Tafreshi [145], Solaimurugan and Velmurugan [146], Semenyuk and, Zhukova [147], Tafreshi [148], Weaver and Dickenson [149], Kere and Lyly [150], Vaziri [151], Semenyuk et al. [152], Tafreshi [153,154], Babich and Semenyuk [155], Biagi and Medico [156], Sheinman and Jabareen [157], Prabu et al. [77], Li and Lin [34], and De Faria [158].
Other buckling analyses include Matsunaga [53], Shen [69], Sofiyev et al. [73], Wang et al. [86], Huang [97], Wang et al. [102], Weaver et al. [118], Huang and Lu [119], Shen and Xiang [120], Diaconu et al. [121], Wang and Dong [125 ], Hilburger and Starnes [143], Semenyuk et al. [144], Tafreshi [145], Zang et al. [176], Goldfeld et al. [186,191], Singh and Babu [188], Wu and Chiu [189], Kadoli and Ganesan [198], and Pinto Correiaa [205].
3.3. Postbuckling Analysis
Shin et al. [115] discussed thermal postbuckled behavior of cylindrical composite shells. Shen [225,226] discussed the same problem with piezoelectric actuators and thermal-dependant properties. Kim et al. [227] presented an 8-node shell element for postbuckling analysis of laminated composite plates and shells. Kundu and Sinha [228] analyzed postbuckling of laminated shells. Kundu et al. [229] performed postbuckling analysis of smart laminated doubly curved shells. Xie and Biggers [230] conducted postbuckling analysis with progressive damage modeling in tailored laminated plates and shells with a cutout. Merazzi et al. [231] employed implicit finite element methods to analyze postbuckling behavior of shellwised tools.
Other studies on postbuckling analysis include Shen [36,37,43,69,124,127,128,133-135], Li and Shen [21,25, 26], Li [41], Shen and Xiang [120], Shen and Li [44, 129], Tafreshi [145,148], Semenyuk and Zhukova [147], Kere and Lyly [150], Sheinman and Jabareen [157], Patel et al. [193,194], Lee and Lee [217], Rahman and Jansen [131], Li and Lin [34], Panda and Ramachandra [130], and Sai Ram and Sreedhar [218].
3.4. Thermal and Hygrothermal Loading
Galishin [232] and Babeshko and Shevchenko [210, 233] performed analysis of the axisymmetric thermoelastoplastic state of laminated transversally isotropic shells. Swamy and Sinha [234] investigated nonlinear analysis of laminated composite shells in hygrothermal environments. Babeshko and Shevchenko [209,235] were interested in thermoelastoplastic state of flexible laminated shells under axisymmetric loading. Cheng and Batra [236] showed thermal effects on laminated composite shells containing interfacial imperfections. Kewei [237] conducted weak formulation study for thermoelastic analysis of thick open laminated shell. Ghosh [238] studied hygrothermal effects on the initiation and propagation of damage in composite shells. Saha and Kalamkarov [239] presented a micromechanical thermoelastic model for sandwich composite shells. El-Damatty et al. [240] performed thermal analysis of composite chimneys using finite shell elements. Roy et al. [241] developed an improved shell element for smart fiber reinforced composite structures under coupled piezothermoelastic loading. Also, Kulikov and Plotinkova [242] constructed a seven parameter geometrically exact shell element to study coupled problem of thermopiezoelectricity in laminated plates and shells.
Studies that treated thermal and/or hygrothermal effects include those of Li and Shen [21,25,26], Ruhi et al. [30], Li [41], Shen [43,44,69,124], Khare et al. [48], Matsunaga [53], Oh and Cho [54], Galishin and Shevchenko [85], Kundu et al. [87], Naidu and Sinha [88], Wang et al. [96,136], Merzlyakov and Galishin [111], Shin [115], Wang and Dong [125], Patel et al. [141,193,194,222], Shevchenko and Babeshko [213,214], Zenkour and Fares [166], Wang and Dai [139], Zhu et al. [140], Singh and Babu [188], Wu and Chiu [189], Kadoli and Ganesan [198], Panda and Singh [93], and in addition to articles that can be found on the dynamic problems in the review by Qatu [3].
3.5. Failure, Delamination and Damage Analyses
Zhang et al. [243] studied progressive failure analysis for advanced grid stiffened composite plates/shells. Ikonomopoulos and Perreux [244] investigated reliability of laminates through a damage tolerance approach. Khoroshun and Babich [245] discussed stability of plates and shells made of homogeneous and composite materials subject to short-term microdamage. Zozulya [246] studied laminated shells with debonding between laminas in temperature field. Larsson [247] discussed discontinuous shell-interface element for delamination analysis of laminated composite structures. Mahdi et al. [248] performed an experimental investigation into crushing behavior of filament-wound laminated cone-cone intersection composite shell. Huang and Lee [249] investigated the static contact crushing of composite laminated shells. Wagner and Balzani [250] performed simulation of delamination in stringer stiffened fiber-reinforced composite shells.
Other studies on failure of composite shells include those of Galishin [232], Xie and Biggers [233], He and Hwang [197], Khoroshun et al. [99, 100], Khoroshun and Babich [108, 114, 163, 245], Mahdi et al. [184], Rezadoust [190], Saleh et al. [199], Solaimurugan and Velmurugan [169], and Ghosh [238].
3.6. Other Analyses
Morozov [251] conducted a theoretical and experimental analysis of filament wound composite shells under compressive loading. Hossain et al. [252], Kim et al. [253] and Szea et al. [254] presented a finite element formulation for the analysis of laminated composite shells. Wu and Burguen [255] studied an integrated approach to shape and laminate stacking sequence optimization of composite shells. Balah and Al-Ghamedy [256] discussed finite element formulation of a third order laminated finite rotation shell element. Trach et al. [257] investigated stability of laminated shells made of materials with one plane of elastic symmetry. Kabir et al. [258] presented a train-gular element for arbitrarily laminated general shells. Kalamkarov et al. [259] delivered an asymptotic model of flexible composite shells of a regular structure. Haussya and Ganghoffer [260] investigated modeling of curved interfaces in composite shells. Roque and Ferreira [261] described new developments in the radial basis functions analysis of shells.
4. Material Complexity
Material complexity in composites occurs in various ways. Composite shells can have active or piezoelectric layers. They can also be braided or made of wood or natural fibers or a combination of materials.
4.1. Piezoelectric Shells
Ren and Parvizi-Majidi [262] presented a model for shape control of cross-ply laminated shells using a piezoelectric actuator. Bhattacharya et al. [263] and Zallo and Gaudenzi [264] presented finite element models for laminated shells with actuation capability. Pinto Correia et al. [265] conducted an analysis of adaptive shell structures using a refined laminated model. Bhattacharya et al. [266] investigated smart laminated shells and deflection control strategy. Xue [267] studied effective dielectric constant of composite shells.
Other studies on piezoelectric shells include Santos et al. [22], Nosier and Ruhi [29], Kioua and Mirza [177], Shen and Xiang [120], Shen [124,127], Alibeigloo [164], Alibeigloo and Nouri [27], Kulikov and Plotnikova [242], Singh and Babu [188], as well as others that dealt with dynamic response [3].
4.2. Other Materials
Picha et al. [268] studied composite polymeric shells. Yan et al. [269] investigated post-tensioned composite shells for concrete confinement. Lopez-Anido et al. [270] studied repair of wood piles using prefabricated polymer composite shells. Burgueño and Bhide [171] discussed shear response of concrete-filled composite cylindrical shells. Other studies on concrete shells include Ferreira [46].
5. Structural Complexity
Structural complexity occurs when the geometry or boundary conditions of the shells deviate from the classical shells described earlier. These include stiffened shells, shells with internal boundaries from cracks, imperfect shells as well as other types of complexities.
5.1. Stiffened Shells
Ambur and Janunky [271] demonstrated a design optimization process while investigating the local buckling behavior of stiffened structures with variable curvature. Optimum design of stiffened cylindrical shells with added T-rings subjected to external pressure was also performed by Bushnell [272]. The reliability of a postbuckled composite isogrid stiffened shell structure subjected to a compression load was studied by Kim [273]. Zeng and Wu [274] performed a post-buckling analysis of stiffened braided cylindrical shells subjected to combined external pressure and axial compression loads. For the same combined loading, Poorveis and Kabir [275] analyzed the static buckling of orthotropic stringer stiffened composite cyclindrical shells. The postbuckling behavior of stringer stiffened panels by using strip elements was determined by Mocker and Reimerdes [276]. Bisagni and Cordisco [277,278] tested stiffened carbon composite stringer-stiffened shells in the postbuckling range until failure. Rao [279] and Rickards et al. [224] used finite elements for buckling and vibration analysis of laminated composite stiffened shells. Prusty [206] used the finite element method to perform a linear static analysis of composite hat-stiffened laminated shells. Bai et al. [280] performed a numerical analysis using a finite element method to investigate the buckling behavior of an advanced grid stiffened structure. Kidane et al. [281] developed an analytical model to study the global buckling load of grid stiffened composite cylinders. De Vries [282] used a hierarchical method to analyze localized buckling of thin-walled stiffened or unstiffened metallic and composite shells. Accardo et al. [283] discuss the design of a combined loads test machine and test fixture to perform experimental investigations on curved reinforced metallic and composite stiffened panels. Linde et al. [284] discussed the development of a virtual test platform used for parametric modeling and simulation of stiffened test shells to study the static behavior in the buckling and postbuckling range. Park et al. [207] and Patel et al. [285] used shell elements to perform both linear and dynamic analysis of laminated stiffened composite shells. An optimization design procedure based on surrogate modeling of stiffened composite shells was presented by Rikards et al. [286]. Using the finite element method, Wong and Teng [287] investigated the buckling behavior of axisymmetric stiffened composite shell structures and Apicella et al. [288] studied the behavior of a stiffened bulkhead subjected to ultimate pressure load. Chen and Guedes Soares [289] modeled ship hulls as stiffened composite panels to perform a strength analysis under sagging moments. Rais-Rohani and Lokits [290] conducted an optimization study to study reinforcement layout and sizing parameters of composite submarine sail structures. Wu et al. [291] conducted an experimental investigation to study the behavior of grid stiffened steel-concrete composite panels under a buckling load. Chen et al. [292] used a nonlinear finite element method to study the thermal mechanical behavior of advanced composite grid stiffened shells with multidelaminations. The finite element method was used by Chen and Xu [293] and by Prusty [294] to study the buckling and postbuckling response of doubly curved stiffened composite panels under general loading. Sahoo and Chakravorty [295] used finite elements to solve a bending problem of a composite stiffened hypar shell subjected to a concentrated load. Zhang et al. [296] and Lu et al. [297] performed a stability analysis of advanced composite grid stiffened shells. A buckling load analysis of composite grid stiffened structures was investigated by the finite element method by He et al. [298]. Progressive failure analysis of composite laminated stiffened plates using a finite strip method for non-linear static analysis was performed by Zahari and El-Zafrany [299].
Studies on stiffened composite shells include Prusty [206], Goldfeld [165], Zhang et al. [243], Wagner and Balzani [250], and others on dynamic analysis [3].
5.2. Shells with Cutouts
Several recent studies have focused on various composite shell structures with cutouts. Hillburger and Starnes [143] and Hillburger [300] performed numerical and experimental studies to determine the effects of unreinforced and reinforced cutouts in composite cylindrical shells subjected to compression loading. Li et al. [301] performed a three-dimensional finite element analysis to study the buckling response of sandwich composite shells with cutouts under axial compression. The princeple of minimum potential energy was used by Madenci and Barut [302] to investigate the effects of an elliptical cutout in a composite cylindrical shell subjected to compression. Nanda and Bandyopadhyay [303] looked at the nonlinear transient responses from static and dynamic analyses of composite cylindrical and spherical shell laminates with cutouts. The finite element method was used to study the bending behavior of laminated composite shells without a cutout [202] and with a central circular cutout [203]. Buckling and post-buckling due to internal pressure and compression loading of composite shells with various size cutouts was investigated through the finite element method by Tafreshi [153]. Xie and Biggers [230] performed analysis on tailored laminated plates and shells with a central cutout subjected to compressive buckling loads. Other studies include Kadoli and Ganesan [198] and Hilburger and Starnes [143]. Asadi et al. [304] considered a layer containing several cavities and cracks and solved the problem under static point forces on the layer.
5.3. Imperfect Shells
Starnes and Hilburger [305] conducted an experimental and analytical study to investigate the effects of initial imperfections on the buckling response of graphite-epoxy cylindrical shells. Arbocz and Hillburger [306] used a probability-based analysis to investigate section properties such as geometric imperfections to determine more accurate buckling-load “knockdown factors”. Biagi and Perugini [307] investigated the buckling behavior of the front composite skirt using linear and nonlinear finite element analysis to study the relationship between various shapes of geometrical imperfections and amplitudes and failure modes. Bisagni [308] studied the buckling and post-buckling characteristics of carbon composite cylindrical shells with geometric imperfections under axial compression using eigenvalue analysis. Carvelli et al. [309,310] performed a non-linear buckling analysis to study the geometric imperfections of composite shells in an underwater sea environment. Hilburger and Starnes [311,312] investigated the effects of imperfections such as shell-wall thickness variations, imperfections due to composite fabrication, shell-end geometric imperfections, and nonuniformly applied end-loads, on the buckling and post-buckling response of un-stiffened thin-walled graphite-epoxy cylindrical shells. Jayachandran et al. [313] also investigated the postbuckling behavior of imperfect thin shells by using secant matrices with the finite element method to study postbuckling behavior of thin composite shells with initial imperfections. Kere and Lyly [150] considered geometric shape imperfections and demonstrated that the best numerical-experimental correlation was achieved with diamond shape imperfecttions. Rahman and Jansen [131] investigated imperfecttion sensitivity of composite cylindrical shells under axial compression using a finite element method. Tafreshi and Bailey [314] investigated the effects of combined loading on imperfect composite shell structures. Wardle and Lagace [315] compared experimental and numerical computations of the buckling response from transversely loaded composite shell structures. Other studies on imperfect shells include Goldfeld [165,185], Vasilenko et al. [107], Cheng and Batra [236], Shen and Li [44], Wang and Zhong [20], and Hilburger and Starnes [223].
Vasilenko et al. [109] studied contact interaction between a laminated shell of revolution and a rigid or elastic foundation.
6. Concluding Remarks
It is interesting to see that despite advances made in computational power, researchers avoided in general usage of 3D theory of elasticity. Experience shows that extensive usage of 3D elements in practical problems is not feasible even with advanced computers. Researchers looked for, developed and used thick shell theories to solve engineering problems. Finite element is the most used method in the analysis. Its ability to treat general boundary conditions, loading and geometry have certainly attributed to its popularity.
Cylindrical shells are still the subject of research of most recent articles. Doubly curved shallow shells have also received considerable interest. These shells can be spherical, barrel, cylindrical, or other shape.
Complicating effects of various kinds have received considerable interest. The use of piezoelectric shells necessitated by various applications and certain advanced materials resulted in considerable literature in the field. Other complicating effect of stiffened shells received some attention.
Looking at recent innovations in the area of composite plates, the authors think that it is a matter of time before these composites start making strong presence in research on shells. Areas of innovation include the use of natural fiber, single-walled and multi-walled carbon nanotubes, varying fiber orientation (both short and long fibers) as we as others. Such innovation are becoming more necessary as composite materials are required to deliver simultaneously structural functions (strength, stiffness, damping, toughness…) and non-structural ones (thermal and electrical conductivity). Both modeling and testing of such composites can be a corner-stone of future research on composite shells.
7. Acknowledgements
The authors thank Mr. Imran Aslam for his help gathering the papers.
REFERENCES
- M. S. Qatu, “Vibration of Laminated Shells and Plates,” Elsevier, Amsterdam, 2004.
- M. S. Qatu, “Recent Research Advances in the Dynamic Behavior of Shells: 1989-2000, Part 1: Laminated Composite Shells,” Applied Mechanics Reviews, Vol. 55, No. 4, 2002, pp. 325-350. doi:10.1115/1.1483079
- M. S. Qatu, R. W. Sullivan and W. Wang, “Recent Research Advances in the Dynamic Behavior of Composite Shells: 2000-2009,” Composite Structures, Vol. 93, No. 1, 2010, pp. 14-31. doi:10.1016/j.compstruct.2010.05.014
- M. S. Qatu, “Accurate Theory for Laminated Composite Deep Thick Shells,” International Journal of Solids and Structures, Vol. 36, No. 19, 1999, pp. 2917-2941. doi:10.1016/S0020-7683(98)00134-6
- P. K. Kapania, “Review on the Analysis of Laminated Shells,” Journal of Pressure Vessel Technology, Vol. 111, 1989, pp. 88-96.
- A. K. Noor and W. S. Burton, “Assessment of Computational Models for Multilayered Composite Shells,” Applied Mechanics Reviews, Vol. 43, No. 4, 1990, pp. 67- 97.
- A. K. Noor and W. S. Burton, “Computational Models for High-Temperature Multilayered Composite Plates and Shells,” Applied Mechanics Reviews, Vol. 45, No. 10, 1992, pp. 419-446. doi:10.1115/1.3119742
- A. K. Noor, W. S. Burton and J. M. Peters, “Assessment of Computational Models for Multilayered Composite Cylinders,” International Journal of Solids and Structures, Vol. 27, No. 10, 1991, pp. 1269-1286. doi:10.1016/0020-7683(91)90162-9
- K. P. Soldatos, “Mechanics of Cylindrical Shells with Non-Circular Cross-Section,” Applied Mechanics Reviews, Vol. 52, No. 8, 1999, pp. 237-274. doi:10.1115/1.3098937
- A. K. Noor, W. S. Burton and C. W. Bert, “Computational Models for Sandwich Panels and Shells,” Applied Mechanics Reviews, Vol. 49, No. 3, 1996, pp. 155-200. doi:10.1115/1.3101923
- A. K. Noor and S. L. Venneri, “High-Performance Computing for Flight Vehicles,” Proceeding of the Symposium of Computer Systems Science and Engineering, Washington DC, 7-9 December 1992, pp. 1-4.
- E. Carrera, “Historical Review of Zig-Zag Theories for Multilayered Plates and Shells,” Applied Mechanics Reviews, Vol. 56, No. 3, 2003, pp. 287-309. doi:10.1115/1.1557614
- E. Carrera, “Theories and Finite Elements for Multilayered, Anisotropic, Composite Plates and Shells,” Journal of Archives of Computational Methods in Engineering, Vol. 9, No. 2, 2002, pp. 87-140. doi:10.1007/BF02736649
- J. N. Reddy, “Mechanics of Laminated Composite Plates and Shells: Theory and Analysis,” 2nd Edition, CRC Press, Boca Raton, 2003.
- J. Ye, “Laminated Composite Plates and Shells: 3D Modeling,” Springer, London, 2003. doi:10.1007/978-1-4471-0095-9
- C. Y. Lee, “Geometrically Correct Laminated Composite Shell Modeling,” VDM Verlag, Lagos, 2008.
- H. S. Shen, “Functionally Graded Materials: Nonlinear Analysis of Plates and Shells,” CRC Press, Boca Raton, 2009. doi:10.1201/9781420092578
- H. Y. Sheng and J. Q. Ye, “A Three-Dimensional State Space Finite Element Solution for Laminated Composite Cylindrical Shells,” Computer Methods in Applied Mechanics and Engineering, Vol. 192, No. 22-24, 2003, pp. 2441-2459. doi:10.1016/S0045-7825(03)00265-2
- C. P. Wu and J. Y. Lo, “Three-Dimensional Elasticity Solutions of Laminated Annular Spherical Shells,” Journal of Engineering Mechanics, Vol. 126, No. 8, 2000, pp. 882-885. doi:10.1061/(ASCE)0733-9399(2000)126:8(882)
- X. Wang and Z. Zhong, “Three-Dimensional Solution of Smart Laminated Anisotropic Circular Cylindrical Shells with Imperfect Bonding,” International Journal of Solids and Structures, Vol. 40, No. 22, 2003, pp. 5901-5921. doi:10.1016/S0020-7683(03)00389-5
- Z. M. Li and H. S. Shen, “Postbuckling Analysis of Three-Dimensional Textile Composite Cylindrical Shells under Axial Compression in Thermal Environments,” Composites Science and Technology, Vol. 68, No. 3-4, 2008, pp. 872-879. doi:10.1016/j.compscitech.2007.08.009
- H. Santos, C. M. M. Soares, C. A. M. Soares and J. N. Reddy, “A Finite Element Model for the Analysis of 3D Axisymmetric Laminated Shells with Piezoelectric Sensors and Actuators,” Composite Structures, Vol. 75, No. 1-4, 2006, pp. 170-178. doi:10.1016/j.compstruct.2006.04.008
- H. Santos, C. M. M. Soares, C. A. M. Soares and J. N. Reddy, “A Finite Element Model for the Analysis of 3D Axisymmetric Laminated Shells with Piezoelectric Sensors and Actuators: Bending and Free Vibrations,” Computers & Structures, Vol. 86, No. 9, 2008, pp. 940-947. doi:10.1016/j.compstruc.2007.04.013
- W. Sprenger, F. Gruttmann and W. Wagner, “Delamination Growth Analysis in Laminated Structures with Continuum-Based 3D-Shell Elements and a Viscoplastic Softening Model,” Computer Methods in Applied Mechanics and Engineering, Vol. 185, No. 2-4, 2000, pp. 123-139. doi:10.1016/S0045-7825(99)00255-8
- Z. M. Li and H. S. Shen, “Postbuckling Analysis of 3D Braided Composite Cylindrical Shells under Torsion in Thermal Environments,” Composite Structures, Vol. 87, No. 3, 2009, pp. 242-256. doi:10.1016/j.compstruct.2008.01.013
- Z. M. Li and H. S. Shen, “Postbuckling of 3D Braided Composite Cylindrical Shells under Combined External Pressure and Axial Compression in Thermal Environments,” International Journal of Mechanical Sciences, Vol. 50, No. 4, 2008, pp. 719-731. doi:10.1016/j.ijmecsci.2007.12.001
- A. Alibeigloo and V. Nouri, “Static Analysis of Functionally Graded Cylindrical Shell with Piezoelectric Layers Using Differential Quadrature Method,” Composite Structures, Vol. 92, No. 8, 2010, pp. 1775-1785. doi:10.1016/j.compstruct.2010.02.004
- C. Fagiano, M. M. Abdalla and Z. Gürdal, “Interlaminar Stress Recovery of Multilayer Composite Shell Structures for Three-Dimensional Finite Elements,” Finite Elements in Analysis and Design, Vol. 46, No. 12, 2010, pp. 1122- 1130. doi:10.1016/j.finel.2010.08.004
- A. Nosier and M. Ruhi, “Three Dimensional Analysis of Laminated Cylindrical Panels with Piezoelectric Layers,” IJE Transactions B: Applications, Vol. 19, No. 1, 2006, pp. 61-72.
- M. Ruhi, A. Angoshtari and R. Naghdabadi, “Thermoelastic Analysis of Thick-Walled Finite-Length Cylinders of Functionally Graded Materials,” Journal of Thermal Stresses, Vol. 28, No. 4, 2005, pp. 391-408. doi:10.1080/01495730590916623
- E. Asadi, W. Wang and M. S. Qatu, “Static and Free Vibration Analyses of Deep Thick Laminated Composite Shells Using 3D and Various Shear Deformation Theories,” Composite Structures, Vol. 94, No. 2, 2012, pp. 494-500. doi:10.1016/j.compstruct.2011.08.011
- R. A. Chaudhuri, “A Nonlinear Zigzag Theory for Finite Element Analysis of Highly Shear-Deformable Laminated Anisotropic Shells,” Composite Structures, Vol. 85, No. 4, 2008, pp. 350-359. doi:10.1016/j.compstruct.2007.11.002
- I. Krejaa and R. Schmidt, “Large Rotations in First-Order Shear Deformation FE Analysis of Laminated Shells,” International Journal of Non-Linear Mechanics, Vol. 41, No. 1, 2006, pp. 101-123. doi:10.1016/j.ijnonlinmec.2005.06.009
- Z. M. Li and Z. Q. Lin, “Non-Linear Buckling and Postbuckling of Shear Deformable Anisotropic Laminated Cylindrical Shell Subjected to Varying External Pressure Loads,” Composite Structures, Vol. 92, No. 2, 2010, pp. 553-567. doi:10.1016/j.compstruct.2009.08.048
- J. Sorić and T. Jarak, “Mixed Meshless Formulation for Analysis of Shell-Like Structures,” Computer Methods in Applied Mechanics and Engineering, Vol. 199, No. 17-20, 2010, pp. 1153-1164. doi:10.1016/j.cma.2009.12.007
- H. S. Shen, “Postbuckling of Shear Deformable Cross-Ply Laminated Cylindrical Shells under Combined External Pressure and Axial Compression,” International Journal of Mechanical Sciences, Vol. 43, No. 11, 2001, pp. 2493- 2523. doi:10.1016/S0020-7403(01)00058-3
- H. S. Shen, “Postbuckling of Shear Deformable Laminated Cylindrical Shells,” Journal of Engineering Mechanics, Vol. 128, No. 3, 2002, pp. 296-307. doi:10.1061/(ASCE)0733-9399(2002)128:3(296)
- V. G. Piskunov, V. E. Verijenko, S. Adali, P. Y. Tabakov, V. K. Prisyazknyouk and S. J. Buryhin, “Rational Transverse Shear Deformation Higher Order Theory of Anisotropic Laminated Plates and Shells,” International Journal of Solids and Structures, Vol. 38, No. 36-37, 2001, pp. 6491-6523. doi:10.1016/S0020-7683(01)00041-5
- R. Iozzi and P. Gaudenzi, “Effective Shear Deformable Shell Elements for Adaptive Laminated Structures,” Journal of Intelligent Material Systems and Structures, Vol. 12, No. 6, 2001, pp. 415-421. doi:10.1106/104538902022722
- S. C. Han, A. Tabiei and W. T. Park, “Geometrically Nonlinear Analysis Of Laminated Composite Thin Shells Using a Modified First-Order Shear Deformable ElementBased Lagrangian Shell Element,” Composite Structures, Vol. 82, No. 3, 2008, pp. 465-474. doi:10.1016/j.compstruct.2007.01.027
- Z. M. Li, “Postbuckling of a Shear-Deformable Anisotropic Laminated Cylindrical Shell under External Pressure in Thermal Environments,” Mechanics of Composite Materials, Vol. 43, No. 6, 2007, pp. 535-560. doi:10.1007/s11029-007-0050-y
- A. M. Zenkour, “Stress Analysis of Axisymmetric Shear Deformable Cross-Ply Laminated Circular Cylindrical Shells,” Journal of Engineering Mathematics, Vol. 40, No. 4, 2001, pp. 315-332. doi:10.1023/A:1017500411490
- H. S. Shen, “The Effects of Hygrothermal Conditions on the Postbuckling of Shear Deformable Laminated Cylindrical Shells,” International Journal of Solids and Structures, Vol. 38, No. 36-37, 2001, pp. 6357-6380. doi:10.1016/S0020-7683(01)00123-8
- H. S. Shen and Q. S. Li, “Thermomechanical Postbuckling of Shear Deformable Laminated Cylindrical Shells with Local Geometric Imperfections,” International Journal of Solids and Structures, Vol. 39, No. 17, 2002, pp. 4525-4542. doi:10.1016/S0020-7683(02)00351-7
- M. Balah and H. N. Al-Ghamedy, “Third Order Shear Deformation Model for Laminated Shells with Finite Rotations: Formulation and Consistent Linearization,” Acta Mech Sinica, Vol. 20, No. 5, 2004, pp. 484-498. doi:10.1007/BF02484271
- A. J. M. Ferreira, “On the Shear-Deformation Theories for the Analysis of Concrete Shells Reinforced with External Composite Laminates,” Strength of Materials, Vol. 35, No. 2, 2003, pp. 128-135. doi:10.1023/A:1023706410615
- W. Zhen and C. Wanji, “A Global-Local Higher Order Theory for Multilayered Shells and the Analysis of Laminated Cylindrical Shell Panels,” Composite Structures, Vol. 84, No. 4, 2008, pp. 350-361. doi:10.1016/j.compstruct.2007.10.006
- R. K. Khare, T. Kant and A. K. Garg, “Closed-Form Thermo-Mechanical Solutions of Higher-Order Theories of Cross-Ply Laminated Shallow Shells,” Composite Structures, Vol. 59, No. 3, 2003, pp. 313-340. doi:10.1016/S0263-8223(02)00245-3
- R. K. Khare and V. Rode, “Higher-Order Closed-Form Solutions for Thick Laminated Sandwich Shells,” Journal of Sandwich Structures and Materials, Vol. 7, No. 4, 2005, pp. 335-358. doi:10.1177/1099636205050260
- A. M. A. Ferreira, C. M. C. Roque and R. M. N. Jorge, “Modeling Cross-Ply Laminated Elastic Shells by a Higher-Order Theory and Multiquadrics,” Computers & Structures, Vol. 84, No. 19-20, 2006, pp. 1288-1299. doi:10.1016/j.compstruc.2006.01.021
- F. Alijani and M. M. Aghdam, “A Semi-Analytical Solution for Stress Analysis of Moderately Thick Laminated Cylindrical Panels with Various Boundary Conditions,” Composite Structures, Vol. 89, No. 4, 2009, pp. 543-550. doi:10.1016/j.compstruct.2008.11.008
- I. F. Pinto Correia, C. M. Mota Soares, C. A. Mota Soares and J. Herskovits, “Analysis of Laminated Conical Shell Structures Using Higher Order Models,” Composite Structures, Vol. 62, No. 3-4, 2003, pp. 383-390. doi:10.1016/j.compstruct.2003.09.009
- H. Matsunaga, “Thermal Buckling of Cross-Ply Laminated Composite Shallow Shells According to a Global Higher-Order Deformation Theory,” Composite Structures, Vol. 81, No. 2, 2007, pp. 210-221. doi:10.1016/j.compstruct.2006.08.008
- J. Oh and M. Cho, “Higher Order Zig-Zag Theory for Smart Composite Shells under Mechanical-Thermo-Electric Loading,” International Journal of Solids and Structures, Vol. 44, No. 1, 2007, pp. 100-127. doi:10.1016/j.ijsolstr.2006.04.017
- M. Yaghoubshahi, E. Asadi and S. J. Fariborz, “A Higher-Order Shell Model Applied to Shells with Mixed Boundary Conditions,” Journal of Mechanical Engineering Science, Vol. 225, No. 2, 2011, pp. 292-303.
- E. Asadi, S. J. Fariborz, “Free Vibration of Composite Plates with Mixed Boundary Conditions Based on HigherOrder Shear Deformation Theory,” Archive of Applied Mechanics, Vol. 82, No. 6, 2012, pp. 755- 766. doi:10.1007/s00419-011-0588-y
- D. J. Benson, Y. Bazilevsa, M. C, Hsua and T. J. R. Hughes, “Isogeometric Shell Analysis: The ReissnerMindlin Shell,” Computer Methods in Applied Mechanics and Engineering, Vol. 199, No. 5-8, 2010, pp. 276-289. doi:10.1016/j.cma.2009.05.011
- Y. Z. Yuan, A. F. Saleeb and A. S. Gendy, “Stress Projection, Layerwise-Equivalent, Formulation for Accurate Predictions of Transverse Stresses in Laminated Plates and Shells,” International Journal of Computational Engineering Science, Vol. 1, No. 1, 2000, pp. 91-138. doi:10.1142/S1465876300000033
- D. Kim and R. A. Chaudhuri, “Effect of Lamination Sequence on the Localization and Shear Crippling Instability in Thick Imperfect Cross-Ply Rings under External Pressure,” Composite Structures, Vol. 80, No. 4, 2007, pp. 504-513. doi:10.1016/j.compstruct.2006.07.011
- [61] D. Kimn and R. A. Chaudhuri, “Effect of Thickness on Buckling of Perfect Cross-Ply Rings under External Pressure,” Composite Structures, Vol. 81, No. 4, 2007, pp. 525-532. doi:10.1016/j.compstruct.2006.09.015
- [62] R. A. Chaudhuri and D. Kim, “Sensitivity of the PostLocalization Response of a Thick Cross-Ply Imperfect Ring to Transverse Young’s Modulus Nonlinearity,” Composite Structures, Vol. 84, No. 1, 2008, pp. 44-56. doi:10.1016/j.compstruct.2007.06.006
- [63] T. Leigh and A. Tafreshi, “Delamination Buckling of Composite Cylindrical Panels under Axial Compressive Load,” ASME 7th Biennial Conference on Engineering Systems Design and Analysis (ESDA2004), Manchester, 19-22 July 2004, pp. 387-396.
- [64] P. Malekzadeh, “A Two-Dimensional Layerwise-Differential Quadrature Static Analysis of Thick Laminated Composite Circular Arches,” Applied Mathematical Modelling, Vol. 33, No. 4, 2009, pp. 1850-1861. doi:10.1016/j.apm.2008.03.008
- [65] J. H. Roh, J. H. Han and I. Lee, “Effects of Shape Memory Alloys on Structural Modification,” Key Engineering Materials, Advances in Nondestructive Evaluation, Vol. 270, 2004, pp. 2120-2125.
- [66] J. H. Roh, I. K. Oh, S. M. Yang, J. H. Han and I. Lee, “Thermal Post-Buckling Analysis of Shape Memory Alloy Hybrid Composite Shell Panels,” Smart Materials and Structures, Vol. 13, No. 6, 2004, p. 1337. doi:10.1088/0964-1726/13/6/006
- [67] W. H. Shin, I. K. Oh and I. Lee, “Nonlinear Flutter of Aerothermally Buckled Composite Shells with Damping Treatments,” Journal of Sound and Vibration, Vol. 324, No. 3-5, 2009, pp. 556-569. doi:10.1016/j.jsv.2009.02.022
- [68] M. Tahani, “Analysis of Laminated Composite Beams Using Layerwise Displacement Theories,” Composite Structures, Vol. 79, No. 4, 2007, pp. 535-547. doi:10.1016/j.compstruct.2006.02.019
- [69] M. S. Qatu and E. Asadi, “Vibration of Doubly Curved Shallow Shells with Arbitrary Boundary Conditions,” Applied Acoustics, Vol. 73, No. 1, 2012, pp. 21-27. doi:10.1016/j.apacoust.2011.06.013
- [70] H. S. Shen, “Buckling and Postbuckling of Laminated Thin Cylindrical Shells under Hygrothermal Environments,” Applied Mathematics and Mechanics, Vol. 22, No. 3, 2001, pp. 270-281. doi:10.1007/BF02437965
- [71] K. P. Soldatos and X. Shu, “Modeling of Perfectly and Weakly Bonded Laminated Plates and Shallow Shells,” Composites Science and Technology, Vol. 61, No. 2, 2001, pp. 247-260. doi:10.1016/S0266-3538(00)00207-4
- [72] R. A. Chaudhuri, K. Balaraman and V. X. Kunukkasseril, “Admissible Boundary Conditions and Solutions to Internally Pressurized Thin Arbitrarily Laminated Cylindrical Shell Boundary-Value Problems,” Composite Structures, Vol. 86, No. 4, 2008, pp. 385-400. doi:10.1016/j.compstruct.2007.12.008
- [73] P. Khosravi, R. Ganesan and R. Sedaghati, “An Efficient Facet Shell Element for Corotational Nonlinear Analysis of Thin and Moderately Thick Laminated Composite Structures,” Computers & Structures, Vol. 86, No. 9, 2008, pp. 850-858.
- [74] A. H. Sofiyev, Z. Zerin and M. Turkmen, “The Buckling of Laminated Cylindrical Thin Shells under Torsion Varying as a Linear Function of Time,” Turkish Journal of Engineering & Environmental Sciences, Vol. 27, 2003, pp. 237-245.
- [75] K. Weicker, R. Salahifar and M. Mohareb, “Shell Analysis of Thin-Walled Pipes. Part I: Field Equations and Solution,” International Journal of Pressure Vessels and Piping, Vol. 87, No. 7, 2010, pp. 402-413. doi:10.1016/j.ijpvp.2010.03.025
- [76] K. Weicker, R. Salahifar and M. Mohareb, “Shell Analysis of Thin-Walled Pipes. Part I: Finite Element Formulation,” International Journal of Pressure Vessels and Piping, Vol. 87, No. 7, 2010, pp. 414-423. doi:10.1016/j.ijpvp.2010.03.026
- [77] J. Kiendla, Y. Bazilevsb, M. C. Hsub, R. Wüchnera and K. U. Bletzingera, “The Bending Strip Method for Isogeometric Analysis of Kirchhof-Love Shell Structures Comprised of Multiple Patches,” Computer Methods in Applied Mechanics and Engineering, Vol. 199, No. 37-40, 2010, pp. 2403-2416. doi:10.1016/j.cma.2010.03.029
- [78] B. Prabu, A. V. Raviprakash and A. Venkatraman, “Parametric Study on Buckling Behaviour of Dented Short Carbon Steel Cylindrical Shell Subjected to Uniform Axial Compression,” Thin-Walled Structures, Vol. 48, No. 8, 2010, pp. 639-649. doi:10.1016/j.tws.2010.02.009
- [79] B. Yu and L. Yang, “Elastic Modulus Reduction Method for Limit Analysis of Thin Plate and Shell Structures,” Thin-Walled Structures, Vol. 48, No. 4-5, 2010, pp. 291- 298. doi:10.1016/j.tws.2009.12.004
- [80] K. S. Challagulla, A. V. Georgiades, G. C. Saha and A. L. Kalamkarov, “Micromechanical Analysis of Grid-Reinforced Thin Composite Generally Orthotropic Shells,” Composites Part B: Engineering, Vol. 39, No. 4, 2008, pp. 627-644. doi:10.1016/j.compositesb.2007.06.005
- [81] M. Jakomina, F. Koselb and T. Kosel, “Thin Double Curved Shallow Bimetallic Shell of translation in a Homogenous Temperature Field by Non-Linear Theory,” Thin-Walled Structures, Vol. 48, No. 3, 2010, pp. 243- 259. doi:10.1016/j.tws.2009.10.005
- [82] A. Ghassemi, A. Shahidi and M. Farzin, “A New Element for Analyzing Large Deformation of THIN NAGHDI SHELL MODEL. Part 1: Elastic,” Applied Mathematical Modelling, Vol. 34, No. 12, 2010, pp. 4267-4277. doi:10.1016/j.apm.2010.05.001
- [83] E. V. Morozov, “The Effect of Filament-Winding Mosaic Patterns on the Strength of Thin-Walled Composite Shells,” Composite Structures, Vol. 76, No. 1-2, 2006, pp. 123- 129. doi:10.1016/j.compstruct.2006.06.018
- [84] A. N. Guz’ and K. I. Shnerenko, “Solution of Two-Dimensional Boundary-Value Problems of the Theory of Thin Composite Shells,” Mechanics of Composite Materials, Vol. 36, No. 4, 2000, pp. 273-276. doi:10.1007/BF02262805
- [85] V. A. Maksimyuk and I. S. Chernyshenko, “Numerical Analysis of the Efficiency of Using Theories of Thin and Thick Composite Shells in Stress Concentration Problems,” Journal of Mathematical Sciences, Vol. 103, No. 3, 2001, pp. 320-324. doi:10.1023/A:1011354010197
- [86] A. Z. Galishin and Y. N. Shevchenko, “Determining the Axisymmetric, Geometrically Nonlinear, Thermoelastoplastic State of Laminated Orthotropic Shells,” International Applied Mechanics, Vol. 39, No. 1, 2003, pp. 56- 63. doi:10.1023/A:1023664032711
- [87] T. L. Wang, W. N. Tang and S. K. Zhang, “Nonlinear Dynamic Response and Buckling of Laminated Cylindrical Shells with Axial Shallow Groove Based on a Semi-Analytical Method,” Journal of Shanghai University, Vol. 11, No. 3, 2007, pp. 223-228.
- [88] C. K. Kundu, D. K. Maiti and P. K. Sinha, “Nonlinear Finite Element Analysis of Laminated Composite Doubly Curved Shells in Hygrothermal Environment,” Journal of Reinforced Plastics and Composites, Vol. 26, No. 14, 2007, pp. 1461-1478. doi:10.1177/0731684407079751
- [89] N. V. S. Naidu and P. K. Sinha, “Nonlinear Finite Element Analysis of Laminated Composite Shells in Hygrothermal Environments,” Composite Structures, Vol. 69, No. 4, 2005, pp. 387-395. doi:10.1016/j.compstruct.2004.07.019
- [90] X. Guo, Y. Y. Lee and C. Mei, “Non-Linear Random Response of Laminated Composite Shallow Shells Using Finite Element Modal Method,” International Journal for Numerical Methods in Engineering, Vol. 67, No. 10, 2006, pp. 1467-1489. doi:10.1002/nme.1672
- [91] B. P. Patel, Y. Nath and K. K. Shukla, “Nonlinear ThermoElastic Buckling Characteristics of Cross-Ply Laminated Joined Conical-Cylindrical Shells,” International Journal of Solids and Structures, Vol. 43, No. 16, 2006, pp. 4810- 4829. doi:10.1016/j.ijsolstr.2005.07.025
- [92] B. P. Patel, K. K. Shuklab and Y. Nath, “Nonlinear Thermoelastic Stability Characteristics of Cross-Ply Laminated Oval Cylindrical/Conical Shells,” Finite Elements in Analysis and Design, Vol. 42, No. 12, 2006, pp. 1061- 1070. doi:10.1016/j.finel.2006.03.009
- [93] J.-C. Xu, Y. Li, F. Wang and R.-H. Liu, “Nonlinear Stability of Double-Deck Reticulated Circular Shallow Spherical Shell,” Applied Mathematics and Mechanics, Vol. 31, No. 3, 2010, pp. 279-290. doi:10.1007/s10483-010-0302-7
- [94] S. K. Panda and B. N. Singh, “Thermal Post-Buckling Analysis of a Laminated Composite Spherical Shell Panel Embedded with Shape Memory Alloy Fibers Using NonLinear Finite Element Methods,” Journal of Mechanical Engineering Science, Vol. 224, No. 4, 2010, pp. 757-769. doi:10.1243/09544062JMES1809
- [95] K. Y. Sze and S. J Zheng, “A Stabilized Hybrid-Stress Solid Element for Geometrically Nonlinear Homogeneous and Laminated Shell Analyses,” Computer Methods in Applied Mechanics and Engineering, Vol. 191, No. 17, 2002, pp. 1945-1966.
- [96] L. G. Andrade, A. M. Awruch and I. B. Morsch, “Geometrically Nonlinear Analysis of Laminate Composite Plates and Shells Using the Eight-Node Hexahedral Element with One-Point Integration,” Composite Structures, Vol. 79, No. 4, 2007, pp. 571-580. doi:10.1016/j.compstruct.2006.02.022
- [97] K. D. Kima, S. C. Hanb and S. Suthasupradit, “Geometrically Non-Linear Analysis of Laminated Compos Structures Using a 4-Node Co-Rotational Shell Element with Enhanced Strains,” International Journal of Non-Linear Mechanics, Vol. 42, No. 6, 2007, pp. 864-881. doi:10.1016/j.ijnonlinmec.2007.03.011
- [98] J. Huang, “Nonlinear Buckling of Composite Shells of Revolution,” Journal of Aerospace Engineering, Vol. 15, No. 2, 2002, pp. 64-71. doi:10.1061/(ASCE)0893-1321(2002)15:2(64)
- [99] A. J. M. Ferreira, J. M. A. C. Sá and A. T. Marques, “Nonlinear Finite Element Analysis of Rubber Composite Shells,” Strength of Materials, Vol. 35, No. 3, 2003, pp. 225-235. doi:10.1023/A:1024656604257
- [100] L. P. Khoroshun, D. V. Babich and E. N. Shikula, “Stability of Cylindrical Shells Made of a Particulate Composite with Nonlinear Elastic Inclusions and Damageable Matrix,” International Applied Mechanics, Vol. 43, No. 10, 2007, pp. 1123-1131. doi:10.1007/s10778-007-0112-9
- [101] L. P. Khoroshun, D. V. Babich and E. N. Shikula, “Stability of Cylindrical Shells Made of a Particulate Composite with Nonlinear Elastic Matrix and Damaged Inclusions,” International Applied Mechanics, Vol. 43, No. 8, 2007, pp. 893-902. doi:10.1007/s10778-007-0090-y
- [102] L. R. Hsia, “Nonlinear Response of Thick Laminated Shells with Inter-Laminar Deformation,” Ph.D. Thesis, University of Utah, Salt Lake, 2006, p. 88.
- [103] X. Wang, G. Lub and D. G. Xiao, “Non-Linear Thermal Buckling for Local Delamination near the Surface of Laminated Cylindrical Shell,” International Journal of Mechanical Sciences, Vol. 44, No. 5, 2002, pp. 947-965. doi:10.1016/S0020-7403(02)00028-0
- [104] J. S. Moitaa, J. Infante Barbosab, C. M. M. Soaresb and C. A. M. Soares, “Sensitivity Analysis and Optimal Design of Geometrically Non-Linear Laminated Plates and Shells,” Computers & Structures, Vol. 76, No. 1-3, 2000, pp. 407-420. doi:10.1016/S0045-7949(99)00164-9
- [105] R. J. Razzaq and A. El-Zafrany, “Non-Linear Stress Analysis of Composite Layered Plates and Shells Using a Mesh Reduction Method,” Engineering Analysis with Boundary Elements, Vol. 29, No. 12, 2005, pp. 1115- 1123. doi:10.1016/j.enganabound.2005.07.001
- [106] E. I. Bespalova and G. P. Urusova, “Contact Interaction between Prestressed Laminated Shells of Revolution and a Flat Foundation,” International Applied Mechanics, Vol. 42, No. 10, 2006, pp. 1137-1144. doi:10.1007/s10778-006-0185-x
- [107] I. F. Pinto Correia, P. G. Martins, C. M. M. Soares, C. A. M. Soares and J. Herskovits, “Modelling and Optimization of Laminated Adaptive Shells of Revolution,” Composite Structures, Vol. 75, No. 1-4, 2006, pp. 49-59. doi:10.1016/j.compstruct.2006.04.003
- [108] A. T. Vasilenko, E. I. Bespalova and G. P. Urusova, “Contact Interaction between a Laminated Shell of Revolution and a Rigid or Elastic Foundation,” International Applied Mechanics, Vol. 41, No. 5, 2005, pp. 520-525. doi:10.1007/s10778-005-0118-0
- [109] L. P. Khoroshun and D. V. Babich, “Stability of Laminated Convex Shells of Revolution with Microdamages in Laminate Components,” International Applied Mechanics, Vol. 42, No. 7, 2006, pp. 810-817. doi:10.1007/s10778-006-0149-1
- [110] A. T. Vasilenko, I. G. Emel’yanov and V. Y. Kuznetsov, “Stress Analysis of Laminated Shells of Revolution with an Imperfect Interlayer Contact,” International Applied Mechanics, Vol. 37, No. 5, 2001, pp. 662-669. doi:10.1023/A:1012316614790
- [111] N. A. Gureeva, Y. V. Klochkov and A. P. Nikolaev, “Analysis of an Arbitrary Loaded Shell of Revolution Based on the Finite Element Method in a Mixed Formulation,” Russian Aeronautics (IZ VUZ), Vol. 53, No. 3, 2010, pp. 7-10. doi:10.3103/S1068799810030025
- [112] V. A. Merzlyakov and A. Z. Galishin, “Thermoelastoplastic Nonaxisymmetric Stress-Strain Analysis of Laminated Shells of Revolution,” International Applied Mechanics, Vol. 37, No. 9, 2001, pp. 1166-1174. doi:10.1023/A:1013282331902
- [113] Z. Ye and Z. Zhou, “The Bending of Composite Shallow Revolutional Shells,” Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 214, No. 6, 2000, pp. 369-376. doi:10.1243/0954410001531953
- [114] V. M. Trach, “Stability of Composite Shells of Revolution,” International Applied Mechanics, Vol. 44, No. 3, 2008, pp. 331-344. doi:10.1007/s10778-008-0049-7
- [115] L. P. Khoroshun and D. V. Babich, “Stability of Shells of Revolution Made of Granular Composite with Damageable Components,” International Applied Mechanics, Vol. 40, No. 9, 2004, pp. 1028-1036. doi:10.1007/s10778-005-0007-6
- [116] W. H. Shin, S. J. Lee, I. K. Oh and I. Lee, “Thermal Post-Buckled Behaviors of Cylindrical Composite Shells with Viscoelastic Damping Treatments,” Journal of Sound and Vibration, Vol. 323, No. 1-2, 2009, pp. 93-111. doi:10.1016/j.jsv.2008.12.029
- [117] K. Bhaskar and G. Balasubramanyam, “Accurate Analysis of End-Loaded Laminated Orthotropic Cylindrical Shells,” Composite Structures, Vol. 58, No. 2, 2002, pp. 209-216. doi:10.1016/S0263-8223(02)00122-8
- [118] V. A. Merglyakov and A. Z. Gatishin, “Analysis of the Thermoelastoplastic Nonaxisymmetric Stress-Strain State of Laminated Circular Cylindrical Shells,” International Applied Mechanics, Vol. 36, No. 2, 2000, pp. 241-246. doi:10.1007/BF02681999
- [119] P. M. Weaver, J. R. Driesen and P. Roberts, “Anisotropic Effects in the Compression Buckling of Laminated Composite Cylindrical Shells,” Composites Science and Technology, Vol. 62, No. 1, 2002, pp. 91-105. doi:10.1016/S0266-3538(01)00186-5
- [120] X. Huang and G. Lu, “Buckling Analysis of Laminated Circular Cylindrical Shells Using a Two-Surface Theory,” International Journal of Mechanical Engineering Education, Vol. 30, No. 2, 2000, pp. 171-183.
- [121] H. S. Shen and Y. Xiang, “Buckling and Postbuckling of Anisotropic Laminated Cylindrical Shells under Combined Axial Compression and Torsion,” Composite Structures, Vol. 84, No. 4, 2008, pp. 375-386. doi:10.1016/j.compstruct.2007.10.002
- [122] C. G. Diaconu, M. Sato and H. Sekine, “Buckling Characteristics and Layup Optimization of Long Laminated Composite Cylindrical Shells Subjected to Combined Loads Using Lamination Parameters,” Composite Structures, Vol. 58, No. 4, 2002, pp. 423-433. doi:10.1016/S0263-8223(02)00130-7
- [123] Y. M. Fu and J. H. Yang, “Delamination Growth for Composite Laminated Cylindrical Shells under External Pressure,” Applied Mathematics and Mechanics, Vol. 28, No. 9, 2007, pp. 1133-1144. doi:10.1007/s10483-007-0901-1
- [124] J. H. Yang and Y. M. Fu, “Delamination Growth of Laminated Composite Cylindrical Shells,” Theoretical and Applied Fracture Mechanics, Vol. 45, No. 3, 2006, pp. 192-203. doi:10.1016/j.tafmec.2006.03.003
- [125] H. S. Shen, “Hygrothermal Effects on the Postbuckling of Composite Laminated Cylindrical Shells,” Composites Science and Technology, Vol. 60, No. 8, 2000, pp. 1227- 1240. doi:10.1016/S0266-3538(00)00062-2
- [126] X. Wang and K. Dong, “Local Buckling for Triangular and Lemniscate Delaminations near the Surface of Laminated Cylindrical Shells under Hygrothermal Effects,” Composite Structures, Vol. 79, No. 1, 2007, pp. 67-75. doi:10.1016/j.compstruct.2005.11.029
- [127] Y. Goldfeld and E. A. Ejgenberg, “On the Different Formulations in Linear Bifurcation Analysis of Laminated Cylindrical Shells,” International Journal of Solids and Structures, Vol. 44, No. 25-26, 2007, pp. 8613-8626. doi:10.1016/j.ijsolstr.2007.06.026
- [128] H. S. Shen, “Postbuckling Analysis of Axially-Loaded Laminated Cylindrical Shells with Piezoelectric Actuators,” European Journal of Mechanics—A/Solids, Vol. 20, No. 6, 2001, pp. 1007-1022. doi:10.1016/S0997-7538(01)01176-7
- [129] H. S. Shen, “Postbuckling of Laminated Cylindrical Shells with Piezoelectric Actuators under Combined External Pressure and Heating,” International Journal of Solids and Structures, Vol. 39, No. 16, 2002, pp. 4271- 4289. doi:10.1016/S0020-7683(02)00262-7
- [130] H. S. Shen and Q. S. Li, “Postbuckling of Cross-Ply Laminated Cylindrical Shells with Piezoelectric Actuators under Complex Loading Conditions,” International Journal of Mechanical Sciences, Vol. 44, No. 8, 2002, pp. 1731-1754. doi:10.1016/S0020-7403(02)00056-5
- [131] S. K. Panda and L. S. Ramachandra, “Postbuckling Analysis of Cross-Ply Laminated Cylindrical Shell Panels under Parabolic Mechanical Edge Loading,” Thin-Walled Structures, Vol. 48, No. 8, 2010, pp. 660-667. doi:10.1016/j.tws.2010.04.010
- [132] T. Rahman and E. L. Jansen, “Finite Element Based Coupled Mode Initial Post-Buckling Analysis of a Composite Cylindrical Shell,” Thin-Walled Structures, Vol. 48, No. 1, 2010, pp. 25-32. doi:10.1016/j.tws.2009.08.003
- [133] X. I. Wangi and D. G. Xiao, “A Study of Buckling of near Surface Local Delamination in a Cylindrical Laminated Shell,” Journal of Reinforced Plastics and Composites, Vol. 20, No. 2001, pp. 1633-1643. doi:10.1177/073168401772679093
- [134] H. S. Shen, “Boundary Layer Theory for the Buckling and Postbuckling of an Anisotropic Laminated Cylindrical Shell. Part I: Prediction under Axial Compression,” Composite Structures, Vol. 82, No. 3, 2008, pp. 346-361. doi:10.1016/j.compstruct.2007.01.024
- [135] H. S. Shen, “Boundary Layer Theory for the Buckling and Postbuckling of an Anisotropic Laminated Cylindrical Shell, Part II: Prediction under External Pressure,” Composite Structures, Vol. 82, No. 3, 2008, pp. 362-370. doi:10.1016/j.compstruct.2007.01.018
- [136] H. S. Shen, “Boundary Layer Theory for the Buckling and Postbuckling of an Anisotropic Laminated Cylindrical Shell, Part III: Prediction under Torsion,” Composite Structures, Vol. 82, No. 3, 2008, pp. 371-381. doi:10.1016/j.compstruct.2007.01.013
- [137] X. Wang, Y. C. Zhang and H. L. Dai, “Critical Strain for a Locally Elliptical Delamination near the Surface of a Cylindrical Laminated Shell under Hydrothermal Effects,” Composite Structures, Vol. 67, No. 4, 2005, pp. 491-499. doi:10.1016/j.compstruct.2004.02.008
- [138] B. Geier, H. R. Meyer-Piening and R. Zimmermann, “On the Influence of Laminate Stacking on Buckling of Composite Cylindrical Shells Subjected to Axial Compression,” Composite Structures, Vol. 55, No. 4, 2002, pp. 467-474. doi:10.1016/S0263-8223(01)00175-1
- [139] P. M. Weaver, J. R. Driesen and P. Robers, “The Effect of Flexural-Twist Anisotropy on Compression Buckling of Quasi-Isotropic Laminated Cylindrical Shells,” Composite Structures, Vol. 55, No. 2, 2002, pp. 195-204. doi:10.1016/S0263-8223(01)00147-7
- [140] X. Wang and H. L. Dai, “Thermal Buckling for Local Delamination near the Surface of Laminated Cylindrical Shells and Delaminated Growth,” Journal of Thermal Stresses, Vol. 26, No. 5, 2003, pp. 423-442. doi:10.1080/713855935
- [141] Y. Zhu, F. Wang and R. H. Liu, “Thermal Buckling of Axisymmetrically Laminated Cylindrically Orthotropic Shallow Spherical Shells Including Transverse Shear,” Applied Mathematics and Mechanics, Vol. 29, No. 3, 2008, pp. 291-300. doi:10.1007/s10483-008-0302-7
- [142] B. P. Patel, K. K. Shukla and Y. Nath, “Thermal Buckling of Laminated Cross-Ply Oval Cylindrical Shells,” Composite Structures, Vol. 65, No. 2, 2004, pp. 217-229. doi:10.1016/j.compstruct.2003.10.018
- [143] J. Yang and Y. Fu, “Analysis of Energy Release Rate for Composite Delaminated Cylindrical Shells Subjected to Axial Compression,” Acta Mechanica Sinica, Vol. 22, No. 6, 2006, pp. 537-546. doi:10.1007/s10409-006-0032-7
- [144] M. W. Hilburger and J. H. Starnes Jr., “Buckling Behavior of Compression-Loaded Composite Cylindrical Shells with Reinforced Cutouts,” International Journal of NonLinear Mechanics, Vol. 40, No. 7, 2005, pp. 1005-1021. doi:10.1016/j.ijnonlinmec.2005.02.001
- [145] N. P. Semenyuk, I. Y. Babich and N. B. Zhukova, “Buckling Instability of Sectional Noncircular Cylindrical Composite Shells under Axial Compression,” Mechanics of Composite Materials, Vol. 39, No. 6, 2003, pp. 541-552. doi:10.1023/B:MOCM.0000010626.76920.69
- [146] A. Tafreshi, “Delamination Buckling and Postbuckling in Composite Cylindrical Shells under Combined Axial Compression and External Pressure,” Composite Structures, Vol. 72, No. 4, 2006, pp. 401-418. doi:10.1016/j.compstruct.2005.01.009
- [147] S. Solaimurugan and R. Velmurugan, “Influence of Fiber Orientation and Stacking Sequence on Petalling of Glass-Polyester Composite Cylindrical Shells under Axial Compression,” International Journal of Solids and Structures, Vol. 44, No. 21, 2007, pp. 6999-7020. doi:10.1016/j.ijsolstr.2007.03.025
- [148] N. P. Semenyuk and N. B. Zhukova, “Initial Postbuckling Behavior of Cylindrical Composite Shells under Axisymmetric Deformation,” International Applied Mechanics, Vol. 42, No. 4, 2006, pp. 461-470. doi:10.1007/s10778-006-0103-2
- [149] A. Tafreshi, “Instability of Delaminated Composite Cylindrical Shells under Combined Axial Compression and Bending,” Composite Structures, Vol. 82, No. 3, 2008, pp. 422-433. doi:10.1016/j.compstruct.2007.01.021
- [150] P. M. Weaver and R. Dickenson, “Interactive Local/Euler Buckling of Composite Cylindrical Shells,” Computers & Structures, Vol. 81, No. 30-31, 2003, pp. 2767-2773. doi:10.1016/S0045-7949(03)00339-0
- [151] P. Kere and M. Lyly, “On Post-Buckling Analysis and Experimental Correlation of Cylindrical Composite Shells with Reissner-Mindlin-Von Kármán Type Facet Model,” Computers & Structures, Vol. 86, No. 2008, pp. 1006- 1013. doi:10.1016/j.compstruc.2007.04.025
- [152] A. Vaziri, “On the Buckling of Cracked Composite Cylindrical Shells under Axial Compression,” Composite Structures, Vol. 80, No. 1, 2007, pp. 152-158. doi:10.1016/j.compstruct.2006.05.007
- [153] N. P. Semenyuk, N. B. Zhukova and V. V. Ostapchuk, “Stability of Corrugated Composite Noncircular Cylindrical Shells under External Pressure,” International Applied Mechanics, Vol. 43, No. 12, 2007, pp. 1380-1389. doi:10.1007/s10778-008-0009-2
- [154] A. Tafreshi, “Buckling and Post-Buckling Analysis of Composite Cylindrical Shells with Cutouts Subjected to Internal Pressure and Axial Compression Loads,” International Journal of Pressure Vessels and Piping, Vol. 79, No. 5, 2002, pp. 351-359. doi:10.1016/S0308-0161(02)00026-1
- [155] A. Tafreshi, “Delamination Buckling and Postbuckling in Composite Cylindrical Shells under External Pressure,” Thin-Walled Structures, Vol. 42, No. 10, 2004, pp. 1379- 1404. doi:10.1016/j.tws.2004.05.008
- [156] I. Y. Babich and N. P. Semenyuk, “The Stability of Cylindrical and Conic Shells Made of Composite Materials with an Elastoplastic Matrix,” International Applied Mechanics, Vol. 36, No. 6, 2000, pp. 697-728. doi:10.1007/BF02681981
- [157] M. Biagi and F. D. Medico, “Reliability-Based Knockdown Factors for Composite Cylindrical Shells under Axial Compression,” Thin-Walled Structures, Vol. 46, No. 12, 2008, pp. 1351-1358. doi:10.1016/j.tws.2008.03.012
- [158] I. Sheinman and M. Jabareen, “Postbuckling of Laminated Cylindrical Shells in Different Formulation,” AIAA Journals, Vol. 43, No. 5, 2005, pp. 1117-1123. doi:10.2514/1.11557
- [159] A. R. De Faria, “Buckling Optimization of Composite Plates and Cylindrical Shells: Uncertain Load Combinations,” Ph.D. Thesis, University of Toronto, Toronto, 2000, p. 167.
- [160] X. Wang, W. Cai and Z. Y. Yu, “An Analytic Method for Interlaminar Stress in a Laminated Cylindrical Shell,” Mechanics of Advanced Materials and Structures, Vol. 9, No. 2, 2002, pp. 119-131. doi:10.1080/153764902753510507
- [161] C. H. Lin and M. H. R. Jen, “Analysis of Laminated Anisotropic Cylindrical Shell by Chebyshev Collocation Method,” Journal of Applied Mechanics, Vol. 70, No. 3, 2003, pp. 391-403. doi:10.1115/1.1574059
- [162] S. Lemanski and P. Weaver, “Optimisation of a 4-Layer Laminated Cylindrical Shell to Meet Given Cross-Sectional Stiffness Properties,” Composite Structures, Vol. 72, No. 2, 2006, pp. 163-176. doi:10.1016/j.compstruct.2004.11.005
- [163] Y.-G. Gong and H. E. Ling-Feng, “Experimental Study and Numerical Calculation of Stability and Load-Carrying Capacity of Cylindrical Shell with Initial Dent,” Journal of the Society for Experimental Mechanics, Vol. 1, No. 1, 2010, pp. 1-11.
- [164] L. P. Khoroshun and D. V. Babich, “Stability of Cylindrical Shells Made of a Laminate Material with Damageable Components,” International Applied Mechanics, Vol. 42, No. 6, 2006, pp. 677-683. doi:10.1007/s10778-006-0135-7
- [165] A. Alibeigloo, “Static Analysis of an Anisotropic Laminated Cylindrical Shell with Piezoelectric Layers Using Differential Quadrature Method,” Mechanical Engineering Science, Vol. 222, No. 6, 2008, pp. 865-880. doi:10.1243/09544062JMES866
- [166] Y. Goldfeld, “The Influence of the Stiffness Coefficients on the Imperfection Sensitivity of Laminated Cylindrical Shells,” Composite Structures, Vol. 64, No. 2, 2004, pp. 243-247. doi:10.1016/j.compstruct.2003.07.002
- [167] A. M. Zenkour and M. E. Fares, “Thermal Bending Analysis of Composite Laminated Cylindrical Shells Using a Refined First-Order Theory,” Journal of Thermal Stresses, Vol. 23, No. 5, 2000, pp. 505-526. doi:10.1080/014957300403969
- [168] Y. Jinhua, F. Yiming and W. Xianqiao, “Variational Analysis of Delamination Growth for Composite Laminated Cylindrical Shells under Circumferential Concentrated Load,” Composites Science and Technology, Vol. 67, No. 3-4, 2007, pp. 541-550. doi:10.1016/j.compscitech.2006.07.036
- [169] T. E. Meink, S. Huybrechts and M. H. H. Shen, “Processing Induced Warpage of Filament Wound Composite Cylindrical Shells,” Journal of Composite Materials, Vol. 36, No. 9, 2002, pp. 1025-1047. doi:10.1177/0021998302036009496
- [170] S. Solaimurugan and R. Velmurugan, “Progressive Crushing of Stitched Glass-Polyester Composite Cylindrical Shells,” Composites Science and Technology, Vol. 67, No. 3-4, 2007, pp. 422-437. doi:10.1016/j.compscitech.2006.09.002
- [171] H. Seif, A. H. Sofiyev, E. Yusufoglu and Z. Karaca, “Semi-Analytical Solution of Stability of Composite Orthotropic Cylindrical Shells under Time Dependant a Periodic Axial Compressive Load,” Iranian Journal of Science and Technology, Vol. 30, No. A3, 2006, pp. 343-347.
- [172] R. Burgueño and K. M. Bhide, “Shear Response of Concrete-Filled FRP Composite Cylindrical Shells,” Journal of Structural Engineering, Vol. 132, No. 6, 2006, pp. 949-960. doi:10.1061/(ASCE)0733-9445(2006)132:6(949)
- [173] L. G. Belozerov and V. A. Kireev, “An Economical Method of Determining the Elasticity Characteristics of the Composite Material of Cylindrical Shells,” Measurement Techniques, Vol. 44, No. 12, 2001, pp. 1224-1233. doi:10.1023/A:1014726305382
- [174] N. P. Semenyuk and V. M. Trach, “Bending of Cord Composite Cylindrical Shells with Noncoincident Directions of Layer Reinforcements and Coordinate Lines,” Mechanics of Composite Materials, Vol. 41, No. 5, 2005, pp. 437-444. doi:10.1007/s11029-005-0069-x
- [175] A. J. Paris and G. A. Costello, “Bending of Cord Composite Cylindrical Shells,” Journal of Applied Mechanics, Vol. 67, No. 1, 2000, pp. 117-127. doi:10.1115/1.321156
- [176] E. A. Movsumov and F. H. Shamiev, “Yield Condition for Circular Cylindrical Shells Made of a Fiber-Reinforced Composite,” Mechanics of Composite Materials, Vol. 42, No. 5, 2006, pp. 459-466. doi:10.1007/s11029-006-0056-x
- [177] Y. Q. Zang, D. Zhang, H. Y. Zhou, H. Z. Mab and T. K. Wang, “Non-Linear Dynamic Buckling of Laminated Composite Shallow Spherical Shells,” Composites Science and Technology, Vol. 60, No. 12-13, 2000, pp. 2361- 2363. doi:10.1016/S0266-3538(00)00031-2
- [178] H. Kioua and S. Mirza, “Piezoelectric Induced Bending and Twisting of Laminated Composite Shallow Shells,” Smart Materials and Structures, Vol. 9, No. 4, 2000, pp. 476-484. doi:10.1088/0964-1726/9/4/310
- [179] A. H. Niemi, “A Bilinear Shell Element Based on a Refined Shallow Shell Mode,” International Journal for Numerical Methods in Engineering, Vol. 81, No. 4, 2010, pp. 485-512.
- [180] I. S. Zarivnyak, “Probability of the Critical State of Glue Joints of a Shallow Laminated Shell with Random Irregularities,” Strength of Materials, Vol. 38, No. 1, 2006, pp. 99-107. doi:10.1007/s11223-006-0021-x
- [181] Y. M. Grigorenko, N. N. Kryukov and Y. I. Ivanova, “Stress Analysis of Biconvex Laminated Orthotropic Shells that Are Shallow to a Variable Degree,” International Applied Mechanics, Vol. 39, No. 6, 2003, pp. 688-695. doi:10.1023/A:1025745925235
- [182] K. M. Gupta, “An Orthotropic Adaptive Shallow Cylindrical Shell on Elastic Foundation,” International Journal of Research and Reviews in Applied Sciences, Vol. 2, No. 1, 2010, pp. 67-87.
- [183] C. P. Wu, Y. C. Hung and J. Y. Lo, “A Refined Asymptotic Theory of Laminated Circular Conical Shells,” European Journal of Mechanics—A/Solids, Vol. 21, No. 2, 2002, pp. 281-300. doi:10.1016/S0997-7538(01)01199-8
- [184] H. S. Das and D. Chakravorty, “A Finite Element Application in the Analysis and Design of Point-Supported Composite Conoidal Shell Roofs: Suggesting Selection Guidelines,” Journal of Strain Analysis for Engineering Design, Vol. 45, 2010, pp. 165-177. doi:10.1243/03093247JSA582
- [185] E. Mahdi, A. M. S. Hamouda, B. B. Sahari and Y. A. Khalid, “Effect of Material and Geometry on Crushing Behaviour of Laminated Conical Composite Shells,” Applied Composite Materials, Vol. 9, No. 5, 2002, pp. 265- 290. doi:10.1023/A:1019695903534
- [186] Y. Goldfeld, “Imperfection Sensitivity of Laminated Conical Shells,” International Journal of Solids and Structures, Vol. 44, No. 3-4, 2007, pp. 1221-1241. doi:10.1016/j.ijsolstr.2006.06.016
- [187] Y. Goldfeld, K. Vervenne, J. Arbocz and F. V. Keulen, “Multi-Fidelity Optimization of Laminated Conical Shells for Buckling,” Structural and Multidisciplinary Optimization, Vol. 30, No. 2, 2005, pp. 128-141. doi:10.1007/s00158-004-0506-9
- [188] E. Mahdi, A. M. S. Hamoudaa, B. B. Saharib and Y. A. Khalid, “Effect of Residual Stresses in a Filament Wound Laminated Conical Shell,” Journal of Materials Processing Technology, Vol. 138, No. 1-3, 2003, pp. 291-296. doi:10.1016/S0924-0136(03)00087-6
- [189] B. N. Singh and J. B. Babu, “Thermal Buckling of Laminated Conical Shells Embedded with and without Piezoelectric Layer,” Journal of Reinforced Plastics and Composites, Vol. 28, No. 7, 2009, pp. 791-812. doi:10.1177/0731684407087133
- [190] C. P. Wu and S. J. Chiu, “Thermoelastic Buckling of Laminated Composite Conical Shells,” Journal of Thermal Stresses, Vol. 24, No. 9, 2001, pp. 881-901. doi:10.1080/014957301750379649
- [191] A. M. Rezadoust, M. Esfandeh and S. A. Sabet, “Crush Behavior of Conical Composite Shells: Effect of Cone Angle and Diameter/Wall Thickness Ratio,” PolymerPlastics Technology and Engineering, Vol. 47, No. 2, 2008, pp. 147-151. doi:10.1080/03602550701815979
- [192] Y. Goldfeld, J. Arbocz and A. Rothwell, “Design and Optimization of Laminated Conical Shells for Buckling,” Thin-Walled Structures, Vol. 43, No. 1, 2005, pp. 107- 133. doi:10.1016/j.tws.2004.07.003
- [193] J. Kosonen, “Specification for Mechanical Analysis of Conical Composite Shells,” M.S. Thesis, Helsinki University of Technology, Helsinki, 2003.
- [194] B. P. Patel, K. K. Shukla and Y. Nath, “Thermal Postbuckling Analysis of Laminated Cross-Ply Truncated Circular Conical Shells,” Composite Structures, Vol. 71, No. 1, 2005, pp. 101-114. doi:10.1016/j.compstruct.2004.09.030
- [195] B. P. Patel, Y. Nath and K. K. Shukla, “Thermal Postbuckling Characteristics of Laminated Conical Shells with Temperature-Dependent Material Properties,” AIAA Journal, Vol. 43, No. 6, 2005, pp. 1380-1388. doi:10.2514/1.13259
- [196] P. Smithmaitrie and H. S. Tzou, “Micro-Control Actions of Actuator Patches Laminated on Hemispherical Shells,” Journal of Sound and Vibration, Vol. 277, No. 4-5, 2004, pp. 691-710. doi:10.1016/j.jsv.2003.09.016
- [197] M. V. Marchuk and N. N. Khomyak, “Refined Mixed Finite Element Solution of the Problem on the Stress State of Laminated Spherical Shells,” International Applied Mechanics, Vol. 37, No. 12, 2001, pp. 1594-1601.
- [198] R. S. He and S. F. Hwang, “Identifying Damage in Spherical Laminate Shells by Using a Hybrid Real-Parameter Genetic Algorithm,” Composite Structures, Vol. 80, No. 1, 2007, pp. 32-41. doi:10.1016/j.compstruct.2006.02.035
- [199] R. Kadoli and N. Ganesan, “A Theoretical Analysis of Linear Thermoelastic Buckling of Composite Hemispherical Shells with a Cutout at the Apex,” Composite Structures, Vol. 68, No. 1, 2005, pp. 87-101. doi:10.1016/j.compstruct.2004.03.003
- [200] M. A. Saleh, E. Mahdi, A. M. S. Hamouda and Y. A. Khalid, “Crushing Behaviour of Composite Hemispherical Shells Subjected to Quasi-Static Axial Compressive Load,” Composite Structures, Vol. 66, No. 1-4, 2004, pp. 487-493. doi:10.1016/j.compstruct.2004.04.073
- [201] H. S. Tzou, W. K. Chai and D. W. Wang, “Micro-Control Actions and Location Sensitivity of Actuator Patches Laminated on Toroidal Shells,” Journal of Vibration and Acoustics, Vol. 126, No. 2, 2006, pp. 284-297. doi:10.1115/1.1687398
- [202] A. B. Mitkevich and A. A. Kul’kov, “Design Optimization and Forming Methods for Toroidal Composite Shells,” Mechanics of Composite Materials, Vol. 42, No. 2, 2006, pp. 95-108. doi:10.1007/s11029-006-0021-8
- [203] K. S. S. Ram and T. S. Babu, “Study of Bending of Laminated Composite Shells. Part 1: Shells without a Cutout,” Composite Structures, Vol. 51, No. 1, 2001, pp. 103-116. doi:10.1016/S0263-8223(00)00129-X
- [204] K. S. S. Ram and T. S. Babu, “Study of Bending of Laminated Composite Shells. Part II: Shells with a Cutout,” Composite Structures, Vol. 51, No. 1, 2001, pp. 117-126. doi:10.1016/S0263-8223(00)00130-6
- [205] S. K. Latifa and P. K. Sinha, “Improved Finite Element Analysis of Multilayered, Doubly Curved Composite Shells,” Journal of Reinforced Plastics and Composites, Vol. 24, No. 4, 2005, pp. 385-404. doi:10.1177/0731684405044899
- [206] I. F. P. Correiaa, J. I. Barbosa, C. M. M. Soares and C. A. M. Soares, “A Finite Element Semi-Analytical Model for Laminated Axisymmetric Shells: Statics, Dynamics and Buckling,” Computers & Structures, Vol. 76, No. 1-3, 2000, pp. 299-317. doi:10.1016/S0045-7949(99)00165-0
- [207] B. G. Prusty, “Linear Static Analysis of Composite HatStiffened Laminated Shells Using Finite Elements,” Finite Elements in Analysis and Design, Vol. 39, No. 12, 2003, pp. 1125-1138. doi:10.1016/S0168-874X(02)00160-9
- [208] T. Park, K. Kim and S. Han, “Linear Static and Dynamic Analysis of Laminated Composite Plates and Shells Using a 4-Node Quasi-Conforming Shell Element,” Composites Part B: Engineering, Vol. 37, No. 2-3, 2006, pp. 237-248. doi:10.1016/j.compositesb.2005.05.007
- [209] F. Alijani, M. M. Aghdam and M. Abouhamze, “Application of the Extended Kantorovich Method to the Bending of Clamped Cylindrical Panels,” European Journal of Mechanics—A/Solids, Vol. 27, No. 3, 2008, pp. 378-388. doi:10.1016/j.euromechsol.2007.05.011
- [210] M. E. Babeshko and Y. N. Shevchenko, “Elastoplastic Axisymmetric Stress-Strain State of Laminated Shells Made of Isotropic and Transversely Isotropic Materials with Different Moduli,” International Applied Mechanics, Vol. 41, No. 8, 2005, pp. 910-916. doi:10.1007/s10778-005-0159-4
- [211] M. E. Babeshko and V. G. Savchenko, “Study of the Elastoplastic Axisymmetric Stress-Strain State of Irradiated Laminated Shells with a Loading History,” International Applied Mechanics, Vol. 37, No. 11, 2001, pp. 1441- 1446. doi:10.1023/A:1014228515259
- [212] M. E. Babeshko and Y. N. Shevchenko, “Thermoelastoplastic Axisymmetric Stress-Strain State of Laminated Orthotropic Shells,” International Applied Mechanics, Vol. 40, No. 12, 2001, pp. 1378-1384. doi:10.1007/s10778-005-0043-2
- [213] M. E. Babeshko, “Thermoelastoplastic State of Flexible Laminated Shells under Axisymmetric Loading along Various Planes Paths,” International Applied Mechanics, Vol. 39, No. 2, 2003, pp. 177-184. doi:10.1023/A:1023957414520
- [214] V. G. Shevchenko and M. E. Babeshko, “The Elastoplastic Axisymmetric Stress-Strain State of Flexible Laminated Shells Exposed to Radiation,” International Applied Mechanics, Vol. 36, No. 9, 2000, pp. 1218-1224. doi:10.1023/A:1009448018861
- [215] Y. N. Shevchenko and M. E. Babeshko, “Numerical Analysis of the Thermoelastoplastic Stress-Strain State of Laminated Orthotropic Shells under Axisymmetric Loading,” Journal of Thermal Stresses, Vol. 29, No. 12, 2006, pp. 1143-1162. doi:10.1080/01495730600712790
- [216] B. P. Maslov, V. B. Zhukov and A. D. Pogrebnyak, “Method of Stressed State Analysis of Thick-Walled GTE Shells from Composite Materials,” Strength of Materials, Vol. 35, No. 4, 2003, pp. 76-382. doi:10.1023/A:1025890308281
- [217] M. Abouhamze, M. M. Aghdam and F. Alijani, “Bending Analysis of Symmetrically Laminated Cylindrical Panels Using the Extended Kantorovich Method,” Mechanics of Advanced Materials and Structures, Vol. 14, No. 7, 2007, pp. 523-530. doi:10.1080/15376490701585967
- [218] H. J. Lee and J. J. Lee, “A Numerical Analysis of the Buckling and Postbuckling Behavior of Laminated Composite Shells with Embedded Shape Memory Alloy Wire Actuators,” Smart Materials and Structures, Vol. 9, No. 6, 2000, pp. 780-787. doi:10.1088/0964-1726/9/6/307
- [219] K. S. Sai-Ram and B. T. Sreedhar, “Buckling of Laminated Composite Shells under Transverse Load,” Composite Structures, Vol. 55, No. 2, 2002, pp. 157-168. doi:10.1016/S0263-8223(01)00143-X
- [220] F. Peng, Y. M. Fu and Y. F. Liu, “On the Durable Critic Load in Creep Buckling of Viscoelastic Laminated Plates and Circular Cylindrical Shells,” Science in China Series G: Physics Mechanics and Astronomy, Vol. 51, No. 7, 2008, pp. 873-882. doi:10.1007/s11433-008-0091-9
- [221] J. Li, Z. H. Xiang and M. D. Xue, “Buckling Analysis of Rotationally Periodic Laminated Composite Shells by a New Multilayered Shell Element,” Composite Structures, Vol. 70, No. 1, 2005, pp. 24-32. doi:10.1016/j.compstruct.2004.08.009
- [222] A. H. Sofiyev, “Torsional Buckling of Cross-Ply Laminated Orthotropic Composite Cylindrical Shells Subject to Dynamic Loading,” European Journal of Mechanics—A/Solids, Vol. 22, No. 2003, pp. 943-951. doi:10.1016/S0997-7538(03)00090-1
- [223] B. P. Patel, Y. Nath and K. K. Shukla, “Thermo-Elastic Buckling Characteristics of Angle-Ply Laminated Elliptical Cylindrical Shells,” Composite Structures, Vol. 77, No. 1, 2007, pp. 120-124. doi:10.1016/j.compstruct.2005.06.001
- [224] M. W. Hilburger and J. H. Starnes Jr., “Effects of Imperfections of the Buckling Response of Composite Shells,” Thin-Walled Structures, Vol. 42, No. 3, 2004, pp. 369- 397. doi:10.1016/j.tws.2003.09.001
- [225] R. Rickards, A. Chate and O. Ozolinch, “Analysis for Buckling and Vibrations of Composite Stiffened Shells and Plates,” Composite Structures, Vol. 51, No. 4, 2001, pp. 361-370. doi:10.1016/S0263-8223(00)00151-3
- [226] H. S. Shen, “Thermal Postbuckling Analysis of Laminated Cylindrical Shells with Piezoelectric Actuators,” Composite Structures, Vol. 55, No. 1, 2002, pp. 13-22. doi:10.1016/S0263-8223(01)00128-3
- [227] H. S. Shen, “Thermal Postbuckling Behavior of Anisotropic Laminated Cylindrical Shells with TemperatureDependent Properties,” AIAA Journal, Vol. 46, No. 1, 2008, pp. 185-193. doi:10.2514/1.31192
- [228] K. D. Kim, G. R. Lomboy and S. C. Han, “A Co-Rotational 8-Node Assumed Strain Shell Element for Postbuckling Analysis of Laminated Composite Plates and Shells,” Computational Mechanics, Vol. 30, No. 4, 2003, pp. 330-342. doi:10.1007/s00466-003-0415-6
- [229] C. K. Kundu and P. K. Sinha, “Postbuckling Analysis of Laminated Composite Shells,” Composite Structures, Vol. 78, No. 3, 2007, pp. 316-324. doi:10.1016/j.compstruct.2005.10.005
- [230] C. K. Kundu, D. K. Maiti and P. K. Sinha, “Postbuckling Analysis of Smart Laminated Doubly Curved Shells,” Composite Structures, Vol. 81, No. 3, 2007, pp. 314-322. doi:10.1016/j.compstruct.2006.08.023
- [231] D. Xie and S. B. Biggers Jr., “Postbuckling Analysis with Progressive Damage Modeling in Tailored Laminated Plates and Shells with a Cutout,” Composite Structures, Vol. 59, No. 2, 2003, pp. 199-216. doi:10.1016/S0263-8223(02)00233-7
- [232] E. Merazzi, R. Degenhardt and K. Rohwer, “Postbuckling Analysis of Composite Shell Structures toward Fast and Accurate Tools with Implicit FEM Methods,” International Journal of Structural Stability and Dynamics, Vol. 10, No. 4, 2010, pp. 941-947. doi:10.1142/S021945541000383X
- [233] A. Z. Galishin, “Analysis of the Axisymmetric Thermoelastoplastic State of Branched Laminated Transversally Isotropic Shells,” International Applied Mechanics, Vol. 36, No. 4, 2000, pp. 538-544.
- [234] M. A. Babeshko and Y. N. Shevchenko, “Axisymmetric Thermoelastoplastic Stress-Strain State of Transversely Isotropic Laminated Shells,” International Applied Mechanics, Vol. 42, No. 6, 2006, pp. 669-676. doi:10.1007/s10778-006-0134-8
- [235] N. Y. Swamy and P. K. Sinha, “Nonlinear Transient Analysis of Laminated Composite Shells in Hygrothermal Environments,” Composite Structures, Vol. 72, No. 3, 2006, pp. 280-288. doi:10.1016/j.compstruct.2004.12.001
- [236] M. E. Babeshko and Y. N. Shevchenko, “Thermoelastoplastic Stress-Strain State of Laminated Shells under Axisymmetric Loading along Arbitrary Plane Paths,” International Applied Mechanics, Vol. 38, No. 12, 2002, pp. 1464-1472. doi:10.1023/A:1023209808061
- [237] Z. Q. Cheng and R. C. Batra, “Thermal Effects on Laminated Composite Shells Containing Interfacial Imperfections,” Composite Structures, Vol. 52, No. 1, 2001, pp. 3- 11. doi:10.1016/S0263-8223(00)00197-5
- [238] D. Kewei, “Weak Formulation Study for Thermoelastic Analysis of Thick Open Laminated Shell,” Mechanics of Advanced Materials and Structures, Vol. 15, No. 1, 2008, pp. 33-39. doi:10.1080/15376490701410588
- [239] A. Ghosh, “Hygrothermal Effects on the Initiation and Propagation of Damage in Composite Shells,” Aircraft Engineering & Aerospace Technology, Vol. 80, No. 4, 2008, pp. 386-399.
- [240] G. C. Saha and A. L. Kalamkarov, “Micromechanical Thermoelastic Model for Sandwich Composite Shells Made of Generally Orthotropic Materials,” Journal of Sandwich Structures and Materials, Vol. 11, No. 1, 2009, pp. 27-56. doi:10.1177/1099636208098147
- [241] A. A. El Damatty, A. S. Awadb and B. J. Vickery, “Thermal Analysis of FRP Chimneys Using Consistent Laminated Shell Element,” Thin-Walled Structures, Vol. 37, No. 1, 2000, pp. 57-76. doi:10.1016/S0263-8231(99)00041-5
- [242] T. Roy, P. Manikandan and D. Chakraborty, “Improved Shell Finite Element for Piezothermoelastic Analysis of Smart Fiber Reinforced Composite Structures,” Finite Elements in Analysis and Design, Vol. 46, No. 9, 2010, pp. 710-720. doi:10.1016/j.finel.2010.03.009
- [243] G. M. Kulikov and V. Plotnikova, “Solution of a Coupled Problem of Thermopiezoelectricity Based on a Geometrically Exact Shell Element,” Mechanics of Composite Materials, Vol. 46, No. 4, 2010, pp. 513-534. doi:10.1007/s11029-010-9152-z
- [244] Z. Zhang, H. Chen and L. Ye, “Progressive Failure Analysis for Advanced Grid Stiffened Composite Plates/Shells,” Composite Structures, Vol. 86, No. 1-3, 2008, pp. 45-54. doi:10.1016/j.compstruct.2008.03.037
- [245] G. Ikonomopoulos and D. Perreux, “Reliability of Composite Laminates through a Damage Tolerance ApproachApplications into Carbon-Epoxy and Glass-Epoxy Composite Shells,” Journal of Composite Materials, Vol. 35, No. 3, pp. 202-236.
- [246] L. P. Khoroshun and D. V. Babich, “Stability of Plates and Shells Made of Homogeneous and Composite Materials Subject to Short-Term Microdamage,” International Applied Mechanics, Vol. 44, No. 3, 2008, pp. 239-267. doi:10.1007/s10778-008-0045-y
- [247] V. V. Zozulya, “Laminated Shells with Debonding Between Laminas in Temperature Field,” International Applied Mechanics, Vol. 42, No. 7, 2006, pp. 842-848. doi:10.1007/s10778-006-0153-5
- [248] R. Larsson, “A Discontinuous Shell-Interface Element for Delamination Analysis of Laminated Composite Structures,” Computer Methods in Applied Mechanics and Engineering, Vol. 193, No. 30-32, 2004, pp. 3173-3194. doi:10.1016/j.cma.2003.08.009
- [249] E. Mahdi, B. B. Sahari, A. M. S. Hamouda and Y. A. Khalid, “An Experimental Investigation into Crushing Behaviour of Filament-Wound Laminated Cone-Cone Intersection Composite Shell,” Composite Structures, Vol. 51, No. 3, 2001, pp. 211-219. doi:10.1016/S0263-8223(00)00132-X
- [250] C. H. Huang and Y. J. Lee, “Static Contact Crushing of Composite Laminated Shells,” Composite Structures, Vol. 63, No. 2, 2004, pp. 211-217. doi:10.1016/S0263-8223(03)00157-0
- [251] W. Wagner and C. Balzani, “Simulation of Delamination in Stringer Stiffened Fiber-Reinforced Composite Shells,” Computers & Structures, Vol. 86, No. 9, 2008, pp. 930- 939. doi:10.1016/j.compstruc.2007.04.018
- [252] E. V. Morozov, “Theoretical and Experimental Analysis of the Deformability of Filament Wound Composite Shells under Axial Compressive Loading,” Composite Structures, Vol. 54, No. 2-3, 2001, pp. 255-260. doi:10.1016/S0263-8223(01)00095-2
- [253] S. J. Hossain, P. K. Sinha and A. H. Sheikh, “A Finite Element Formulation for the Analysis of Laminated Composite Shells,” Computers & Structures, Vol. 82, No. 20- 21, 2004, pp. 1623-1638. doi:10.1016/j.compstruc.2004.05.004
- [254] K. D. Kim, C. S. Lee and S. C. Han, “A 4-Node Co-Rotational ANS Shell Element for Laminated Composite Structures,” Composite Structures, Vol. 80, No. 2, 2007, pp. 234-252. doi:10.1016/j.compstruct.2006.05.003
- [255] K. Y. Szea, L. Q. Yaoa and T. H. H. Pian, “An EighteenNode Hybrid-Stress Solid-Shell Element for Homogenous and Laminated Structures,” Finite Elements in Analysis and Design, Vol. 38, No. 4, 2002, pp. 353-374. doi:10.1016/S0168-874X(01)00089-0
- [256] J. Wu and R. Burguen, “An Integrated Approach to Shape and Laminate Stacking Sequence Optimization of FreeForm FRP Shells,” Computer Methods in Applied Mechanics and Engineering, Vol. 195, No. 33-36, 2006, pp. 4106-4123. doi:10.1016/j.cma.2005.07.015
- [257] M. Balah and H. N. Al-Ghamedy, “Finite Element Formulation of a Third Order Laminated Finite Rotation Shell Element,” Computers & Structures, Vol. 80, No. 26, 2002, pp. 1975-1990. doi:10.1016/S0045-7949(02)00222-5
- [258] V. M. Trach and A. V. Podvornyi, “Stability of Laminated Shells Made of Materials with One Plane of Elastic Symmetry,” International Applied Mechanics, Vol. 40, No. 5, 2004, pp. 573-579. doi:10.1023/B:INAM.0000037305.78333.21
- [259] H. R. H. Kabir and K. Al-Shaleh, “Three-Node Triangular Element for Arbitrarily Laminated General Shells,” Composite Structures, Vol. 77, No. 1, 2007, pp. 18-29. doi:10.1016/j.compstruct.2005.05.013
- [260] A. L. Kalamkarov, G. Duvaut and F. Lene, “A New Asymptotic Model of Flexible Composite Shells of a Regular Structure,” International Journal of Engineering Science, Vol. 40, No. 2002, pp. 333-343. doi:10.1016/S0020-7225(01)00065-9
- [261] B. Haussya and J. F. Ganghoffer, “Modelling of Curved Interfaces in Composite Shells,” International Journal of Mechanical Sciences, Vol. 48, No. 11, 2006, pp. 1234- 1245. doi:10.1016/j.ijmecsci.2006.06.007
- [262] C. M. C. Roque and A. J. M. Ferreira, “New Developments in the Radial Basis Functions Analysis of Composite Shells,” Composite Structures, Vol. 87, No. 2, 2009, pp. 141-150. doi:10.1016/j.compstruct.2008.05.011
- [263] L. Ren and A. Parvizi-Majidi, “A Model for Shape Control of Cross-Ply Laminated Shells Using a Piezoelectric Actuator,” Journal of Composite Materials, Vol. 40, No. 2006, pp. 1271-1285. doi:10.1177/0021998305057437
- [264] P. Bhattacharya, H. Suhail and P. K. Sinha, “Finite Element Analysis and Distributed Control of Laminated Composite Shells Using LQR/IMSC Approach,” Aerospace Science and Technology, Vol. 6, No. 4, 2002, pp. 273-281. doi:10.1016/S1270-9638(02)01159-8
- [265] A. Zallo and P. Gaudenzi, “Finite Element Models for Laminated Shells with Actuation Capability,” Computers & Structures, Vol. 81, No. 8-11, 2003, pp. 1059-1069. doi:10.1016/S0045-7949(03)00002-6
- [266] I. F. Pinto Correia, C. M. Mota Soares, C. A. Mota Soares and J. Herskovits, “Analysis of Adaptive Shell Structures Using a Refined Laminated Model,” Composite Structures, Vol. 66, No. 1-4, 2004, pp. 261-268. doi:10.1016/j.compstruct.2004.04.047
- [267] P. Bhattacharya, H. Suhail and P. K. Sinha, “Smart Laminated Shells and Deflection Control Strategy with Optimal Voltage,” Journal of Reinforced Plastics and Composites, Vol. 19, No. 16, 2000, pp. 1293-1316. doi:10.1106/H2WR-TRYC-LNDF-7BM5
- [268] Q. Xue, “Effective Dielectric Constant of Composite with Interfacial Shells,” Physica B: Condensed Matter, Vol. 344, No. 1-4, 2004, pp. 129-132. doi:10.1016/j.physb.2003.05.001
- [269] A. Picha, J. Haina, Y. Protsb and H. J. Adler, “Composite Polymeric Particles with ZnS Shells,” Polymer, Vol. 46, No. 19, 2005, pp. 7931-7944. doi:10.1016/j.polymer.2005.06.062
- [270] Z. Yan, C. P. Pantelides and L. D. Reaveley, “Post-Tensioned FRP Composite Shells for Concrete Confinement,” Journal of Composites for Construction, Vol. 11, No. 1, 2007, pp. 81-90. doi:10.1061/(ASCE)1090-0268(2007)11:1(81)
- [271] R. Lopez-Anido, A. P. Michael, T. C. Sandford and B. Goodell, “Repair of Wood Piles Using Prefabricated Fiber-Reinforced Polymer Composite Shells,” Journal of Performance of Constructed Facilities, Vol. 19, No. 1, 2005, pp. 78-87. doi:10.1061/(ASCE)0887-3828(2005)19:1(78)
- [272] D. R. Ambur and N. Jaunky, “Optimal Design of GridStiffened Panels and Shells with Variable Curvature,” Composite Structures, Vol. 52, No. 2, 2001, pp. 173-180. doi:10.1016/S0263-8223(00)00165-3
- [273] D. Bushnell, “Global Optimum Design of Externally Pressurized Isogrid Stiffened Cylindrical Shells with Added T-Rings,” International Journal of Non-Linear Mechanics, Vol. 37, No. 4-5, 2002, pp. 801-837. doi:10.1016/S0020-7462(01)00100-7
- [274] T. D. Kim, “Postbuckled Behavior of Composite Isogrid Stiffened Shell Structure,” Advanced Composite Materials, Vol. 9, No. 3, 2000, pp. 253-263.
- [275] T. Zeng and L. Wu, “Post-Buckling Analysis of Stiffened Braided Cylindrical Shells under Combined External Pressure and Axial Compression,” Composite Structures, Vol. 60, No. 4, 2003, pp. 455-466. doi:10.1016/S0263-8223(03)00018-7
- [276] D. Poorveis and M. Z. Kabir, “Buckling of Discretely Stringer-Stiffened Composite Cylindrical Shells under Combined Axial Compression and External Pressure,” Scientia Iranica, Vol. 13, No. 2, 2006, pp. 113-123.
- [277] T. Mocker and H. G. Reimerdes, “Load Carrying Capability of Stringer Stiffened Curved Composite Panels in the Postbuckling Region,” Proceedings of the European Conference on Spacecraft Structures, Materials and Mechanical Testing 2005 (ESA SP-581), Noordwijk, 10-12 May 2005, p. 1077.
- [278] C. Bisagni and P. Cordisco, “Testing of Stiffened Composite Cylindrical Shells in the Postbuckling Range until Failure,” AIAA Journal, Vol. 42, No. 9, 2004, pp. 1806- 1817. doi:10.2514/1.6088
- [279] C. Bisagni and P. Cordisco, “Post-Buckling and Collapse Experiments of Stiffened Composite Cylindrical Shells Subjected to Axial Loading and Torque,” Composite Structures, Vol. 73, No. 2, 2006, pp. 138-149. doi:10.1016/j.compstruct.2005.11.055
- [280] K. P. Rao, “Study of the Behaviour of Laminated Composite Beam, Plate and Shell Structures Using Some Specifically Developed Finite Elements,” Journal of Spacecraft Technology, Vol. 10, No. 2, 2000, pp. 1-13.
- [281] R. Bai, M. Wang and H. Chen, “Buckling Behavior of Composite AGS with Delamination,” Acta Materiae Compositae Sinica, Vol. 22, No. 4, 2005, pp. 136-141.
- [282] S. Kidane, G. Li and J. Helms, S. S. Pang and E. Woldesenbet, “Buckling Load Analysis of Grid Stiffened Composite Cylinders,” Composites Part B: Engineering, Vol. 34, No. 1, 2003, pp. 1-9. doi:10.1016/S1359-8368(02)00074-4
- [283] J. De Vries, “Analysis of Localized Buckling of Cylindrical Shell Using a Hierarchical Approach,” AIAA, Vol. 11, 2006, p. 8061.
- [284] A. F. Accardo, F. Ricci, D. Lucariello, P. Polese, B. Leone, D. Cozzolino and F. S. Palmiero, “Design of a Combined Loads Machine for Tests on Fuselage Barrels and Curved Panels,” AIAA, Vol. 2, 2004, p. 1249.
- [285] P. Linde, A. Schulz and W. Rust, “Influence of Modelling and Solution Methods on the FE-Simulation of the PostBuckling Behaviour of Stiffened Aircraft Fuselage Panels,” Composite Structures, Vol. 73, No. 2, 2006, pp. 229- 236. doi:10.1016/j.compstruct.2005.11.048
- [286] S. N. Patel, P. K. Datta and A. H. Sheikh, “Dynamic Instability Analysis of Laminated Composite Stiffened Shell Panels Subjected to In-Plane Harmonic Edge Loading,” Structural Engineering & Mechanics, Vol. 22, No. 4, 2006, pp. 483-510.
- [287] R. Rikards, H. Abramovich, K. Kalnins and J. Auzins, “Surrogate Modeling in Design Optimization of Stiffened Composite Shells,” Composite Structures, Vol. 73, No. 2, 2006, pp. 244-251. doi:10.1016/j.compstruct.2005.11.046
- [288] H. T. Wong and J. G. Teng, “Buckling Behaviour of Model Steel Base Shells of the Comshell Roof System,” Journal of Constructional Steel Research, Vol. 62, No. 1-2, 2006, pp. 4-19. doi:10.1016/j.jcsr.2005.04.015
- [289] A. Apicella, E. Armentani, R. Esposito and M. Pirozzi, “Finite Element Analysis of a Composite Bulkhead Structure,” Key Engineering Materials, Vol. 348-349, 2007, pp. 348-349.
- [290] N. Z. Chen and C. G. Soares, “Longitudinal Strength Analysis of Ship Hulls of Composite Materials under Sagging Moments,” Composite Structures, Vol. 77, No. 1, 2007, pp. 36-44. doi:10.1016/j.compstruct.2005.06.002
- [291] M. Rais-Rohani and J. Lokits, “Reinforcement Layout and Sizing Optimization of Composite Submarine Sail Structures,” Structural and Multidisciplinary Optimization, Vol. 34, No. 1, 2007, pp. 75-90. doi:10.1007/s00158-006-0066-2
- [292] D. Wu, Y. Xu and Q. Wan, “Global Buckling Load Analysis of Grid Stiffened Composite Panels,” Acta Materiae Compositae Sinica, Vol. 24, No. 2, 2007, pp. 168- 172.
- [293] H.-R. Chen, B.-H. Zhou and R.-X. Bai, “Thermal-Mechanical Buckling Behavior of Advanced Composite Grid Stiffened Shell with Multi-Delaminations,” Mechanical Engineers, Vol. 25, No. 8, 2008, pp. 58-63.
- [294] W. Chen and X. Xu, “Buckling and Postbuckling Response Analysis of the Doubly-Curved Composite Shell by Nonlinear FEM,” Acta Materiae Compositae Sinica, Vol. 25, No. 2, 2008, pp. 178-187.
- [295] B. G. Prusty, “Free Vibration and Buckling Response of Hat-Stiffened Composite Panels under General Loading,” International Journal of Mechanical Sciences, Vol. 50, No. 8, 2008, pp. 1326-1333. doi:10.1016/j.ijmecsci.2008.03.003
- [296] S. Sahoo and D. Chakravorty, “Bending of Composite Stiffened Hypar Shell Roofs under Point Load,” Journal of Engineering Mechanics, Vol. 134, No. 6, 2008, pp. 441- 454. doi:10.1061/(ASCE)0733-9399(2008)134:6(441)
- [297] Z. F. Zhang, H. R. Chen and R. X. Bai, “Stability Analysis of Advanced Composite Grid Stiffened Cylindrical Shell,” Journal of Dalian University of Technology, Vol. 48, No. 5, 2008, pp. 631-640.
- [298] W. Lu, Y. Ma, W. Liang and Z. Lu, “Analysis System of Stability and Strength for Airframe Composite Stiffened Plate/Shell,” Acta Aero Astr Sinica, Vol. 30, No. 5, 2009, p. 895.
- [299] J. X. He, G. Q. He, M.-F. Ren and X. Hou, “Buckling Load Analysis of Composite Grid Stiffened Structure Skirts,” Journal of Solid Rocket Technology, Vol. 32, No. 3, 2009, p. 331.
- [300] R. Zahari and A. El-Zafrany, “Progressive Failure Analysis of Composite Laminated Stiffened Plates Using the Finite Strip Method,” Composite Structures, Vol. 87, No. 1, 2009, pp. 63-70. doi:10.1016/j.compstruct.2007.12.006
- [301] M. W. Hilburger, “Buckling and Failure of CompressionLoaded Composite Laminated Shells with Cutouts,” AIAA, Vol. 6, 2007, p. 6366.
- [302] J. Li, Z. H. Xiang and M. D. Xue, “Three-Dimensional Finite Element Buckling Analysis of Honeycomb Sandwich Composite Shells with Cutouts,” Computers, Materials & Continua, Vol. 2, No. 1, 2005, pp. 139-150.
- [303] E. Madenci and A. Barut, “The Influence of Geometric Irregularities on the Linear Buckling of Cylindrical Shells with an Elliptic Cutout,” 44th AIAA/ASME/ASCE/AHS/ ASC Structures, Structural Dynamics, and Materials Conference, Reston, 2003, p. 1929.
- [304] N. Nanda and J. N. Bandyopadhyay, “Nonlinear Transient Response of Laminated Composite Shells,” Journal of Engineering Mechanics, Vol. 134, No. 11, 2008, pp. 983-991. doi:10.1061/(ASCE)0733-9399(2008)134:11(983)
- [305] E. Asadi, A. R. Farrahi and S. J. Fariborz, “Mixed Mode Axisymmetric Annular Cracks in a Finite Layer: Off Angle Crack Initiation,” Theoretical and Applied Fracture Mechanics, Vol. 56, No. 2, 2011, pp. 112-121. doi:10.1016/j.tafmec.2011.10.007
- [306] J. J. H. Starnes, M. W. Hilburger and M. P. Nemeth, “The Effects of Initial Imperfections on the Buckling of Composite Cylindrical Shells,” In: P. Grant and C. Q. Rousseau, Eds., Composite Structures: Theory and Practice, American Society for Testing and Materials, ASTM STP1383, West Conshohocken, 2000, pp. 529-550.
- [307] J. Arbocz and M. W. Hilburger, “Towards a Probabilistic Preliminary Design Criterion for Buckling Critical Composite Shells,” AIAA Journal, Vol. 43, No. 8, 2003, pp. 1823-1827.
- [308] M. Biagi and P. Perugini, “Nonlinear Analysis of the Vega Launcher First Stage Composite Skirts with Geometrical Imperfections,” 48th AIAA/ASME/ASCE/AHS/ ASC Structures, Structural Dynamics, and Materials Conference, Hawaii, 2007.
- [309] C. Bisagni, “Numerical Analysis and Experimental Correlation of Composite Shell Buckling and Post-Buckling,” Composites Part B: Engineering, Vol. 31, No. 8, 2000, pp. 655-667. doi:10.1016/S1359-8368(00)00031-7
- [310] V. Carvelli, N. Panzeri and C. Poggi, “Buckling Strength of GFRP Under-Water Vehicles,” Composites Part B: Engineering, Vol. 32, No. 2, 2001, pp. 89-101. doi:10.1016/S1359-8368(00)00063-9
- [311] V. Carvelli, N. Panzeri and C. Poggi, “Effects of Material Failure on Buckling Behaviour of Medium-Thick GFRP Cylindrical Shells for Submarine Applications,” ASME Applied Mechanics Division, Vol. 248, 2001, pp. 81-94.
- [312] M. N. Hilburger and J. H. Starnes Jr., “High-Fidelity Nonlinear Analysis of Compression-Loaded Composite Shells,” Proceedings of the 42nd AIAA/ASME/ASCE/ AHS/ASC Structures, Structural Dynamics, and Materials Conference, Seattle, 2001, p. 1394.
- [313] M. W. Hilburger and J. H. Starnes Jr., “Effects of Imperfections on the Buckling Response of Compression-Loaded Composite Shells,” Proceedings of the 41st AIAA/ ASME/ ASCE/ AHS/ASC Structures, Structural Dynamics, and Materials Conference, Atlanta, 2000, p. 1387.
- [314] S. A. Jayachandran, V. Kalyanaraman and R. Narayanan, “Marguerre Shell Type Secant Matrices for the Postbuckling Analysis of Thin, Shallow Composite Shells,” Structural Engineering & Mechanics, Vol. 18, 2004, pp. 41- 58.
- [315] A. Tafreshi and C. G. Bailey, “Instability of Imperfect Composite Cylindrical Shells under Combined Loading,” Composite Structures, Vol. 80, No. 1, 2007, pp. 49-64. doi:10.1016/j.compstruct.2006.02.031
- [316] B. L. Wardle and P. A. Lagace, “Bifurcation, Limit-Point Buckling, and Dynamic Collapse of Transversely Loaded Composite Shells,” AIAA Journal, Vol. 38, No. 3, 2000, pp. 507-516. doi:10.2514/2.989

