Open Journal of Polymer Chemistry
Vol.4 No.3(2014), Article
ID:48553,7
pages
DOI:10.4236/ojpchem.2014.43004
Meyer-Neldel Rule in Plasma Polythiophene Thin Films
J. Cuauhtemoc Palacios1,2, M. Guadalupe Olayo3, Guillermo J. Cruz3*, J. A. Chávez-Carvayar2
1Facultad de Ingeniería, Universidad Autónoma del Estado de México, Toluca, México.
2Instituto de Investigaciones en Materiales, Universidad Nacional Autónoma de México, México D.F., México.
3Departamento de Física, Instituto Nacional de Investigaciones Nucleares, Ocoyoacac, México
Email: *guillermoj.cruz@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 May 2014; revised 28 June 2014; accepted 8 July 2014
ABSTRACT
In polymers, the electronic activation energy depends on the fragmentation, crosslinking, dopants, moisture and in general on the structure-environment interaction. This has a special importance in plasma polymers because fragmentation and crosslinking are usually higher than in other polymers. In this work, DC electrical conductivity of polythiophene thin films prepared by plasma (pPTh) was studied using the Meyer-Neldel (MN) rule to calculate the characteristic MN energy and temperature as a function of moisture and metallic dopants. The experimental data for pPTh synthesized in different conditions indicated that EM = 32 meV and TM = 373 K, suggesting a thermally activated conduction mechanism; however, in polymer-metal matrices with metal concentration higher than the percolation threshold, the conduction mechanism is different causing that the MN rule was only partially fulfilled. The congruence of the experimental data with the multiexcitation entropy model is discussed.
Keywords:Polythiophene, Plasma, Conductivity, Meyer-Neldel Rule, Multi-Excitation Entropy Model

1. Introduction
The electrical conductivity of semiconductors and many other materials following thermally activated processes obeys exponential expressions similar to the Arrhenius equation, see Equation (1) where k is the Boltzmann constant, Ea is the activation energy and so is a pre-exponential factor. In this expression, s tends to so when T increases at high values. However, materials at high temperatures change to liquid or gas phases, or even more, they may degrade modifying so to a hypothetical conductivity if the material survive at high temperature. Considering multiple possibilities in these conditions, huge variations in so are observed. However, as so correlates with Ea, in 1937 Meyer and Neldel proposed an empirical expression called the Meyer-Neldel (MN) rule [1] [2] , see Equation (2), where σoo is another MN pre-exponential factor and EM = kTM is a characteristic energy (the MN energy) of the material at TM (the MN characteristic temperature). Similar expressions have been observed not only in conductivity but also in many other thermally activated phenomena. The MN rule is also found in literature as the compensation law and has been observed in crystalline, amorphous, organic and inorganic materials [3] [4] , but a physical interpretation of EM and σoo is still not clear enough.
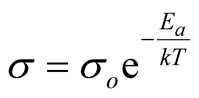 (1)
(1)
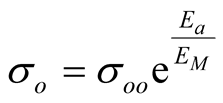 (2)
(2)
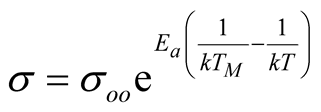 (3)
(3)
Equation (3) is another expression of σ from equations (1) and (2), where it is obvious that at T = TM, the electrical conductivity becomes σoo. This implies a single crossing point for all lines in lnσo vs 1/T plots at σoo. However, in many experiments TM has been calculated beyond the thermal stability of materials and Ea has been considered a function of intrinsic and extrinsic factors like chemical structure, doping, electric field across the sample, etc. [5] .
Several models have been proposed to explain the MN rule in materials with different external variables to influence the thermally activated conductivity [6] . For example, in amorphous semiconductors, conductivity has been explained by means of short-range interactions of the electronic bonding orbitals, instead of a band edge as in crystals [2] . The Arrhenius equation has been also used widely to describe the electrical conductivity of organic films formed by plasma, particularly in thin polymeric films [7] . Pinto [8] explained the semiconductor behavior using an inhomogeneous disordered metallic model, called metallic islands, where the material is composed of crystalline regions, islands, surrounded by disordered regions in which the charge transport between islands defines the macroscopic conductivity.
In semiconductor polymers synthesized by plasma, it has been observed that the structure and properties are highly sensitive to the energy distribution in the reactor during the synthesis. Thus, both depends on one hand on the synthesis conditions as pressure in the reactor, power applied, monomer flow, gas carrier, etc., which influence the structure of materials [9] and on the other hand on external, extrinsic factors, as moisture, temperature, interaction with light, electrical field, etc. In this way, the movement of charge carriers through intermolecular barriers in a polymer synthesized by plasma becomes a multivariable function of thermally activated conduction mechanisms associated with intrinsic and extrinsic factors.
In this study, DC electrical conductivity of polythiophene thin films synthesized by plasma is studied using the Meyer-Neldel rule to find EM and TM with intrinsic factors and moisture as the principal external factor of a multiple thermally activated conduction mechanism. Conductivity was measured by the two-probe method in heating-cooling cycles. The structure of the polymeric films was characterized using X-ray diffraction.
2. Experimental
Thin films of pPTh were synthesized by rf glow discharges with thiophene (Fluka, 98%) in vapor phase in a glass cylindrical reactor at 13.56 MHz, 10 W and 7 × 10−2 mbar with synthesis times of 150, 240 and 300 min [10] . The reactor is 21 cm long and 9 cm diameter with two stainless steel flanges and two flat electrodes of 6 cm diameter. The flanges were maintained at the same electrical potential as the electrodes. The pPTh films were formed on the inner reactor walls and removed swelling them with acetone and distilled water. The thickness of films was measured with a Mitutoyo micrometer.
The structure of pPTh was studied by X-ray diffraction (XRD) with data collected from 5˚ to 60˚ 2q in a Siemens D5000 diffractometer. The electric conductivity of pPTh was calculated measuring the resistance in a capacitive arrangement with pPTh films between copper electrodes using an OTTO MX620 Digital Multimeter and a High Impedance Analog Multimeter in a temperature range from 25˚C to 100˚C. In order to study the moisture effect on the conductivity, each sample was analyzed applying four heating-cooling cycles, with steps of 1˚C and 1 min/step (approximately). In each cycle, the samples were slowly heated up to 100˚C, and later they were left at the atmosphere until the room temperature was reached. After that, another cycle started again.
Due to the plasma energy distribution between electrodes, the reactor has different energetic zones [9] -[11] , however, the most representative are those from the central zone, which are studied in this work. In order to compare the electrical conductivity of pPTh with other plasma polythiophene compounds, polymer-metal composites of pPTh, Ag and Cu, PTh-Ag-Cu, were synthesized as described in [12] with metal concentration values, x, from 0 to 0.8. All samples are stable in the normal air atmosphere.
3. Results
pPTh is mainly an amorphous material with some little evidence of ordered zones, a maximum of 6%, calculated following the method described by M. Kakudo [13] based in the intensity of diffraction near 12˚ (see Figure 1). The evolution of diffraction patterns indicates that in general terms, the ordered zones increase in pPTh as the synthesis time grows. In a model with metallic islands surrounded by insulating barriers, a material with better structural order could enhance their electrical conductivity as the model suggest by Pinto [8] . In pPTh, conductivity obeys the Arrhenius equation (see Figure 2 and Figure 3), in an interval of almost three orders of magnitude. However, conductivity shows no evident correlation with ordered structures or synthesis time to apply a crystalline islands model.
Considering the external factors in conductivity, the polymer films of this work absorb moisture from the atmosphere which is partially lost and reabsorbed in the heating-cooling cycles applied to study conductivity. Figures 2(a)-(c) show typical Arrhenius plots of pPTh synthesized at 150, 240 and 300 min. The filled and unfilled symbols belong to cooling and heating cycles, respectively. Higher conductivities correspond to the first heating cycles. Figure 2(d) shows the Arrhenius behavior for all synthesis times of the last cooling cycles, in which only the remaining humidity is present.
A characteristic of polymers synthesized by plasma is partial fragmentation and crosslinking caused by the frequent collisions of energetic plasma particles. Fragmentation produces short paths of electric charges in the structure which results in low conductivity. On the opposite, crosslinking increases the structural stiffness resulting, among other effects, in a slight increase of the electric conductivity, mainly because the new paths of charges created in the resulting network. As both, fragmentation and cross inking produce opposite effects; the final conductivity of the polymer depends on their balance.
Moisture absorbed in polymers enhances the electric conductivity due to the contribution of water in the transference of charges which is added to the intrinsic conduction mechanisms due to the chemical structure. In networked polymers, moisture swells the material filling the voids with water polar molecules which excite the nearest atoms modifying considerably Ea, as can be observed in the slopes of Arrhenius plots. However, as the content of moisture reduces, conductivity and Ea tends to that of the intrinsic material, as can be seen in the crosslinked polymers without absorbed moisture, shown in Figure 2(d). In the final heating-cooling cycle the polymers show a more linear behavior and higher Ea than the first cycles.
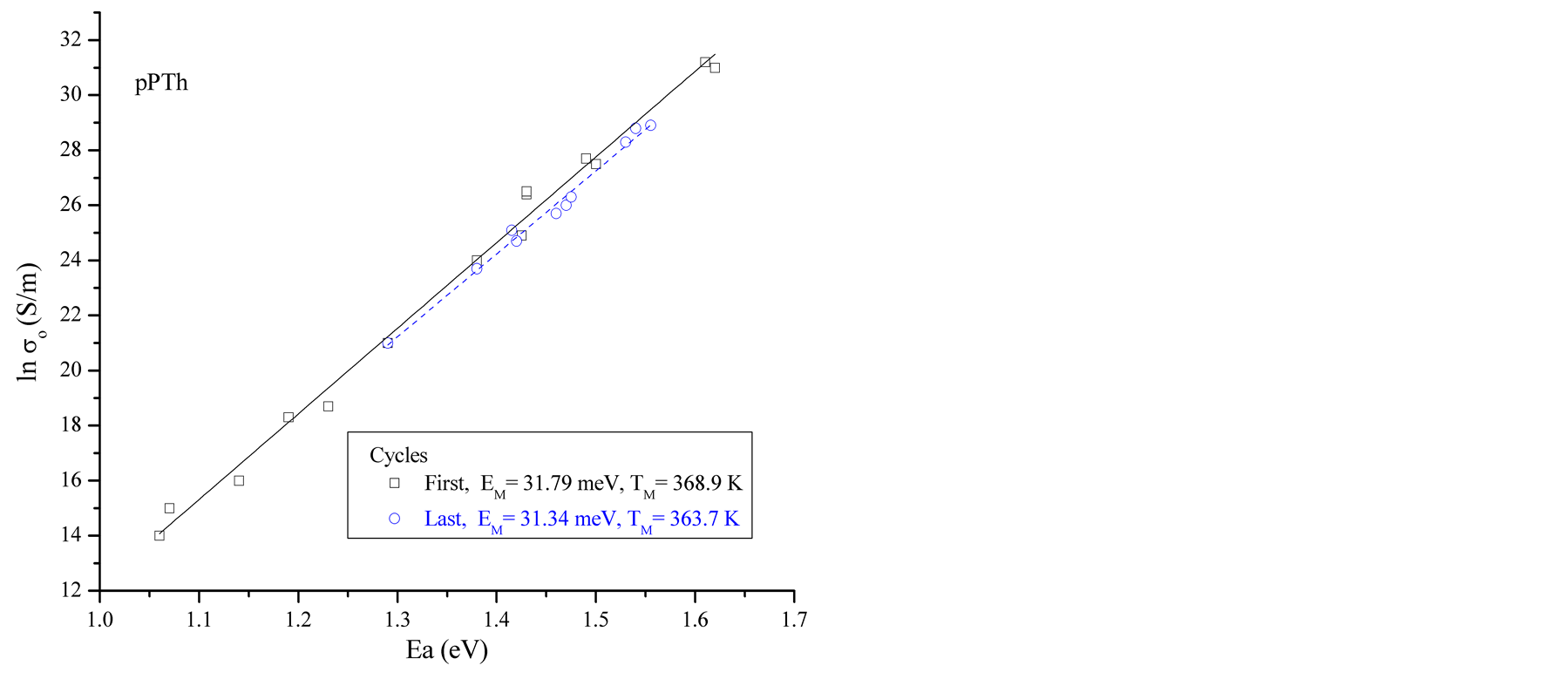
Ea and σo can be obtained from the linear fits in Figure 2. The data show variation of Ea, from 0.45 to 1.59 eV. lnσo vs Ea data are plotted at different synthesis times corresponding to samples in the heating-cooling cycles for all reactor zones, see Figure 3(a). Values corresponding to the first heating and the last cooling cycles in all synthesis times are plotted in Figure 3(b). No correlation is observed between synthesis times and humidity with EM.
From the linear fits of plots similar to the presented in Figure 3(a), but including all the synthesis times and reactor zones, a mean MN characteristic energy EM = 32 meV was obtained. This value is in the expected range for semiconductors, between 25 meV and 100 meV [1] , and corresponds to a mean TM = 373 K which was inside the temperature range studied in this work.
4. Discussion
Several attempts have been realized to identify the main variables of the MN rule. For example, in amorphous silicon, the rule has been attributed to the temperature dependence of Fermi energy and to the diminution of the band gap with increases of temperature [14] . Widenhorn [15] and coworkers propose that the MN rule arises for a thermally activated property when both, intrinsic and extrinsic processes involving impurities, contribute. In this case the property is considered the sum of two thermally activated mechanisms which can cause a spread in

Figure 1. XRD patterns of pPTh for different time of synthesis.
 (a)
(a)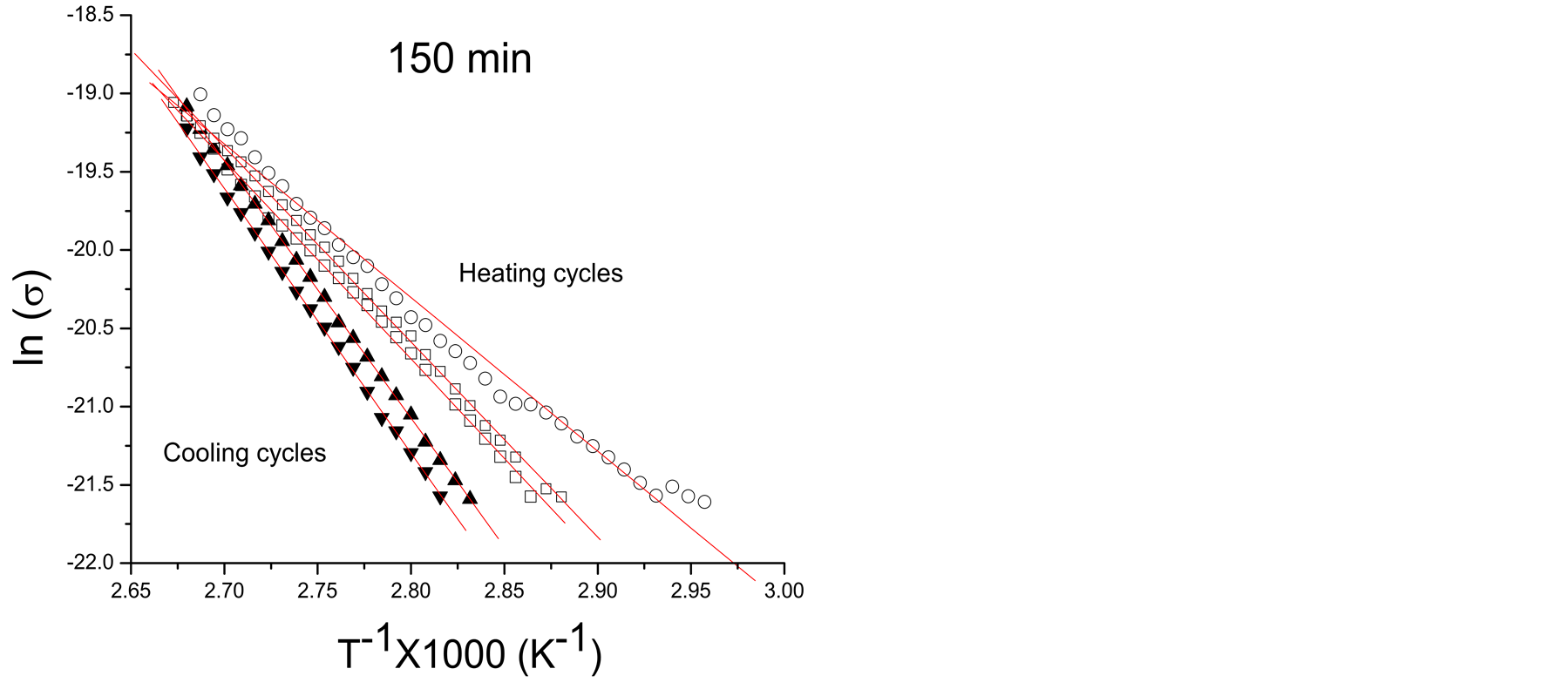 (b)
(b)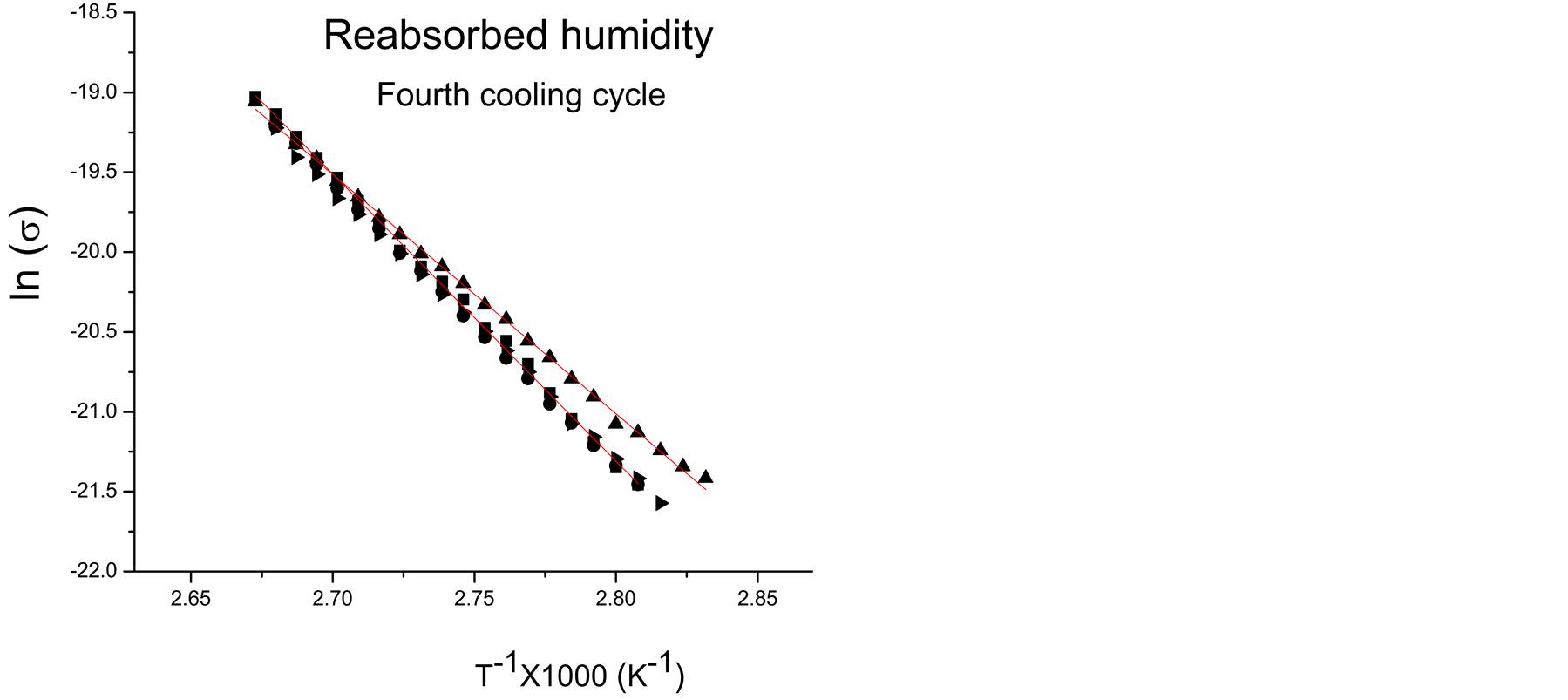 (c)
(c) (d)
(d)
Figure 2. Typical Arrhenius plots of pPTh synthesized at (a) 150, (b) 240 and (c) 300 min, in heating-cooling cycles, (d) Arrhenius behavior corresponding to the last cooling step, only with the reabsorbed humidity. Filled and unfilled symbols belong to cooling and heating steps, respectively.
 (a)
(a)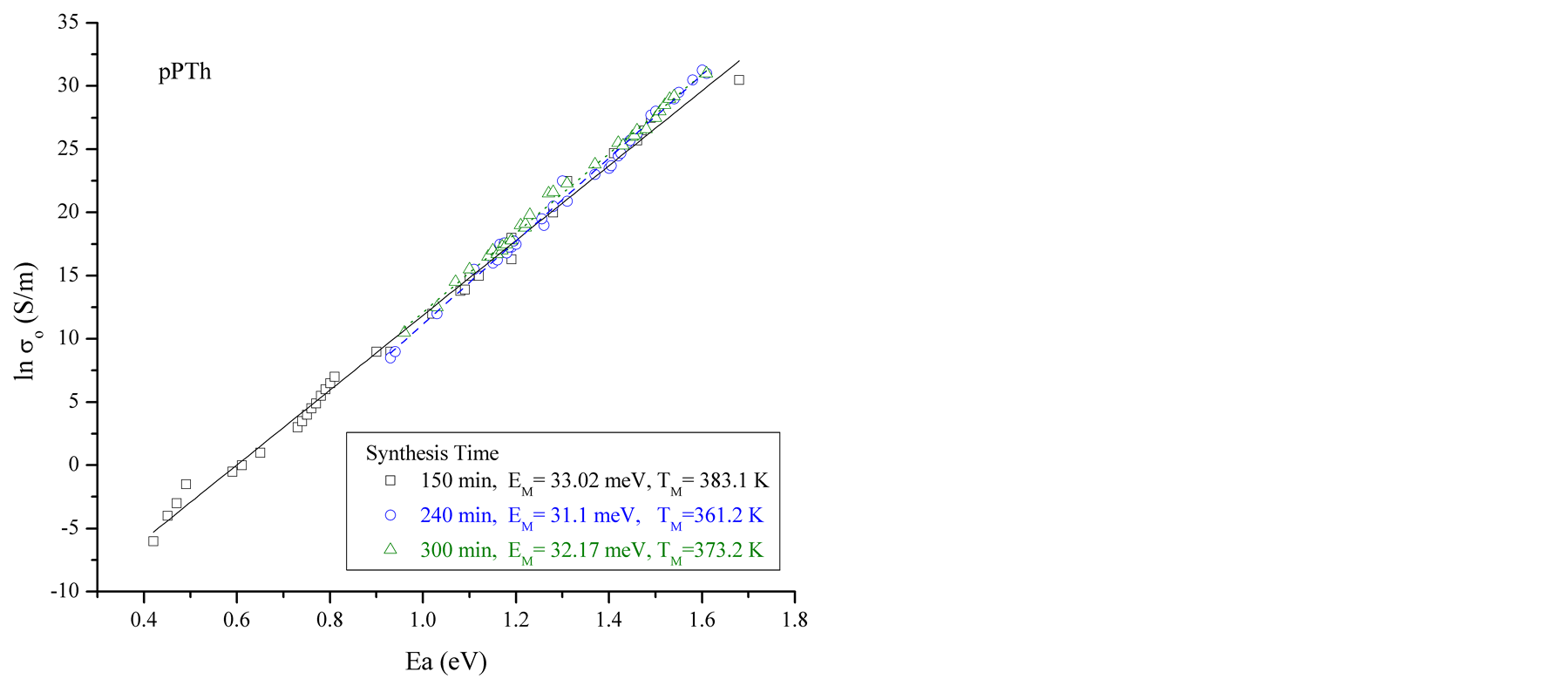 (b)
(b)
Figure 3. (a) pPTh lnσ0 vs Ea plots. The data are plotted in heating-cooling cycles for polymers synthesized at 150, 240 and 300 min of reaction, (b) first and last heating cycles for all synthesis times. A good agreement with the MN rule is observed.
the effective activation energy. Fishchuk and coworkers [16] used the effective medium approximation (EMA) applied to disordered organic semiconductors finding that the MN rule is a consequence of hopping transport in a random system with variable carrier concentration.
In this work, structural factors such as crystallinity, fragmentation and crosslinking are considered intrinsic and moisture was considered the only extrinsic factor. However, although moisture contributes in a substantial way in the spread of the activation energy, a considerable change in EM is not observed. It is clear from these results that multiple factors modify the electrical conductivity. Because the MN rule has been observed in many phenomena and many different materials, crystalline and amorphous, the more general model to explain the results is perhaps the multi-excitation entropy (MEE) model, discussed by Yelon and coworkers [3] . The MEE model is based in the statement that when a large number of excitations must be collected in order to overcome a barrier, there are a large number of ways in which can be done and a large entropy of activation can be associated. From the revision made by Yelon, the MN rule is observed when the activation energy is larger than both, the energies of excitations, normally infrared vibrations or phonons, and kT, both conditions are fulfilled by p-PTh thin films of this work.
In order to apply the MEE model with the experimental data of this work, in Figure 4 lnσo vs Ea plots for pPTh-Ag-Cu composites are presented. When the metal volume fraction, (x), is lower than the percolation threshold fraction (xc), the electrical conductivity of PTh-Ag-Cu was thermally activated, similar to the pPTh conductivity. Very linear behaviour of lnσ vs 1/T was observed [14] for all metal concentrations. However, high x values results in metallic conductivity, decreasing the activation energy, which breaks the thermally activated conduction mechanism, producing that the MN rule is not fulfilled in the complete range. This is because another conduction mechanism appears at x ≥ xc that is much more effective than the thermally activated mechanism. However, if both mechanisms could be treated separately, the MN rule could be applied in different ways in both, although more data would be needed in this study. But even Merlo and Frisbie, [17] in a study of field effect transistors, report basically the same EM, 33 ± 3 eV, in regioregular poly (3-hexylthiophene) nanofibres. It has been found crystallinity in the structure of nanofibres with polymer chains packed in lamellar sheets. Regardless of the charge transport mechanism used to explain the conductivity, or the very different structures, the MEE model proposes that EM is on the order of the excitation energy which must be collected by the material to permit activation. In these cases, Yelon refers to the system as strongly-coupled with the thermodynamic behavior, and the MEE model is agree with the experimental evidences.
5. Conclusion
The electrical conductivity of plasma polythiophenes as a function of moisture, temperature and metallic dopants

Figure 4. PTh-Ag lnσ0 vs Ea plots. The MN rule is not fulfilled for samples with x upper xc (percolation threshold fraction).
was studied from a Meyer-Neldel rule perspective. Two thermally activated processes could be associated with the MN rule: one structural, such as fragmentation, crosslinking and crystallinity and another external, as interaction with moisture. The MN rule was observed for pPTh, independently of the absorbed humidity with a characteristic energy, EM = 32 meV and a characteristic temperature, TM = 373 K. However, metals in polymer matrices beyond the percolation limit break the thermally activated conduction mechanisms which govern the pPTh conductivity, producing that the MN rule is only partially fulfilled. A reasonable explanation of the pPTh conductivity is provided by the multi-excitation entropy model which is congruent with the experimental observations in this work.
Acknowledgements
J. C. Palacios acknowledges CONACyT for his postdoctoral grant, projects 47467 and 80735.
References
- Sharma, S.K., Sagar, P., Gupta, H., Kumar, R. and Mehra, R. (2007) Meyer-Neldel Rule in Se and S-Doped Hydrogenated Amorphous Silicon. Solid-State Electronics, 51, 1124-1128. http://dx.doi.org/10.1016/j.sse.2007.06.007
- Overhof, H. and Thomas, P. (1989) Electronic Transport in Hydrogenated Amorphous Semiconductors. SpringerVerlag, Berlin.
- Yelon, A., Movaghar, B. and Crandall, R.S. (2006) Multi-Excitation Entropy: Its Role in Thermodynamics and Kinetics. Reports on Progress in Physics, 69, 1145-1194. http://dx.doi.org/10.1088/0034-4885/69/4/R04
- Dalvi, A., Reddy, N.P. and Agarwal, S.C. (2012) The Meyer-Neldel Hopping Conduction. Solid State Communications, 152, 612-615. http://dx.doi.org/10.1016/j.ssc.2012.01.018
- Mehta, N. and Kumar, A. (2006) Applicability of Meyer-Neldel Rule for Isothermal Crystallization in Glassy Se70 Te30-XSbX Alloys. Material Letters, 60, 725-729.
- Mehta, N. (2010) Meyer-Neldel Rule in Chalcogenide Glasses: Recent Observations and Their Consequences. Current Opinion in Solid State and Materials Science, 14, 95-106. http://dx.doi.org/10.1016/j.cossms.2010.06.001
- Shi, F. (1996) Recent Advances in Polymer Thin Films Prepared by Plasma Polymerization; Synthesis, Structural Characterization, Properties and Applications. Surface and Coatings Technology, 82, 1-15. http://dx.doi.org/10.1016/0257-8972(95)02621-5
- Pinto, N.J., Shah, P.D., McCormick, B.J. and Kahol, P.K. (1996) Dependence of Conducting State of Polyaniline Films on Moisture. Solid State Communications, 11, 931-934. http://dx.doi.org/10.1016/0038-1098(95)00779-2
- Cruz, G.J., Morales, J., Castillo-Ortega, M.M. and Olayo, R. (1997) Synthesis of Polyaniline Films by Plasma Polymerization. Synthetic Metals, 88, 213-218. http://dx.doi.org/10.1016/S0379-6779(97)03853-8
- Olayo, M.G., Colín, E., Cruz, G.J., Morales, J. and Olayo, R. (2009) Accelerated Nitridation and Oxidation by Plasma on Polyethylene. European Physical Journal, Applied Physics, 48, Article ID: 30501. http://dx.doi.org/10.1051/epjap/2009166
- Olayo, M.G., Morales, J., Cruz, G.J., Barocio, S.R. and Olayo, R. (2003) Numerical and Experimental Analysis of the Plasma in the Synthesis of Polyaniline. Journal of Polymer Science, Part B: Polymer Physics, 41, 1501-1508. http://dx.doi.org/10.1002/polb.10493
- Palacios, J.C., Cruz, G.J., Olayo, M.G. and Chávez-Carvayar, J.A. (2009) Characterization of Hydrophobic and Hydrophilic Polythiophene-Silver-Copper Thin Film Composites Synthesized by DC Glow Discharges. Surface and Coatings Technology, 203, 3032-3036. http://dx.doi.org/10.1016/j.surfcoat.2009.03.020
- Kakudo, M. and Kasai, N. (1972) X-Ray Diffraction by Polymers. Kodansha, Japan.
- Street, R.A. (1991) Hydrogenated Amorphous Silicon. Cambridge University Press, Cambridge.
- Widenhorn, R., Rest, A. and Bodegom, E. (2002) The Meyer-Neldel Rule for a Property Determined by Two Transport Mechanisms. Journal of Applied Physics, 91, 6524-6528.
- Fishchuk, I.I., Kadashchuk, A.K., Genoe, J., Ullah, M., Sitter, H., Singh, Th.B., Sariciftci, N.S. and Bassler, H. (2010) Temperature Dependence of the Charge Carrier Mobility in Disordered Organic Semiconductors at Large Carrier Concentrations. Physical Review B, 81, 1-12. http://dx.doi.org/10.1103/PhysRevB.81.045202
- Merlo, J. and Frisbie, D. (2004) Field Effect Transport and Trapping in Regioregular Polythiophene. Journal of Physical Chemistry B, 108, 19169-19179. http://dx.doi.org/10.1021/jp047023a
NOTES

*Corresponding author.

