Open Journal of Polymer Chemistry
Vol.2 No.3(2012), Article ID:22206,8 pages DOI:10.4236/ojpchem.2012.23012
Non-Isothermal Degradation Kinetics of Hybrid Copolymers Containing Thermosensitive and Polypeptide Blocks
1Department of Materials Science, Burgas Prof. Assen Zlatarov University, Burgas, Bulgaria
2Institute of Polymers, Bulgarian Academy of Sciences, Sofia, Bulgaria
3Department of Physical Chemistry, Burgas Prof. Assen Zlatarov University, Burgas, Bulgaria
Email: *sturmanova@btu.bg
Received May 11, 2012; revised June 18, 2012; accepted June 28, 2012
Keywords: Self-Associating Hybrid Copolymers; N-Carboxyanhydride of Z-L-Lysine (Z-L-Lys-NCA); Thermal Stability; Properties; Non-Isothermal Degradation; Kinetics
ABSTRACT
Novel, self-associating hybrid copolymers were synthesized via controlled ring-opening polymerization of N-carboxyanhydride of Z-L-lysine (Z-L-Lys-NCA), initiated by amino-functional macroinitiators. A poly(N-isopropylacrylamide) (PNIPAm)-based macroinitiator containing 10 mol% of polyoxyethylene grafts and a terminal primary amine group in the form of ammonium hydrochloride (PNIPAm-g-PEО) was synthesized and used to initiate the ammoniummediated ring-opening polymerization of NCA described by Dimitrov and Schlaad [1]. Thus, hybrid copolymers ((PNIPAm-g-PEO)-b-PLys) with controlled molar-mass characteristics and functionality were obtained. The potential applications of PNIPAm-based copolymers in the systems for controlled drug release, immobilization of enzymes and protein purification have aroused great interest in the studies of their properties and behaviour. The thermal stability and thermodynamic properties of the copolymers obtained were studied. The differential thermal analysis of polyfunctional hybrid copolymers (PNIPAm-g-PEO)-b-PLys) showed that thermooxidative destruction occurs in two stages: primary, of the unstable fragments (grafted chains of PEO); and secondary, of the main polymer chains of poly(N-isopropylacrylamide) and poly(L-lysine). The kinetics of thermal degradation was evaluated and the values of the activation energy of the degradation process, changes of Gibbs free energy, enthalpy and entropy for the formation of the activated complex were also calculated.
1. Introduction
The synthesis of polypeptide-based hybrid block copolymers is an area that has been under study for the past three decades. Initially, this field suffered from limitations in the synthesis of the polypeptide components that required excessive sample purification and fractionation to obtain well-defined copolymers. The vast improvements in Ncarboxyanhydride (NCA) of α-amino acid polymerizations now allow the synthesis of hybrid block copolymers of controlled characteristics (molar mass, sequence, composition and molar-mass distribution). Such well-defined materials will greatly assist the identification of new self-assembled structures using ordered polypeptide segments as well as yield new materials with a wide range of tunable properties [2]. Copolymers containing reactive functional groups find application in the fields of surface modification and catalysis, and can also be used as precursors in the synthesis of new materials with complex architectures [3,4].
Hybrid block copolymers have found applications in different biomedical fields such as tissue engineering, implantation of medical devices and artificial organs, bone repair, and drug delivery [5]. The presence of functional groups along the chains could lead to significant changes in their behavior in the solid state and in solution [6]. Subsequent transformations of these groups may further lead to polymers with desired functionalities [7,8].
Recently, much effort has been directed to the development of intelligent hybrid copolymers that respond to internal or external stimuli, in particular, pH, temperature, redox potential, light, magnetic field, and ultrasound, either reversibly or non-reversibly. Stimuli-sensitive polymers have emerged as novel programmable delivery systems in which the release of the encapsulated contents can be readily modulated by the stimulus. The stimuli responsive release may result in significantly enhanced therapeutic efficacy and minimized possible side effects [9].
Temperature-responsive polymer systems generally comprise polymers such as poly(N-isopropylacrylamide), which exhibit a volume phase transition at a certain temperature. Thermodynamically, these transitions are governed by entropic effects due to the release of ordered water molecules in the vicinity of the polymer and the dissolution process itself, and enthalpic effects due to intraand intermolecular forces and solvation, for example, hydrogen bonding and hydrophobic interactions [9].
To our knowledge, no experimental work has been reported so far on the study of the thermal stability of hybrid copolymers containing thermosensitive and polypeptide blocks and for their thermal degradation in presence of oxygen or inert atmosphere.
Thermogravimetric analysis (TGA) is one of the thermal analysis techniques used to measure the mass change, thermal decomposition and thermal stability of polymer materials. Overall kinetics can be easily obtained by measuring the change in mass of a sample with time based on isothermal or non-isothermal thermogravimetric data [10- 12]. Some valuable parameters, such as apparent activation energy E, pre-exponential factor A, and reaction order n can be calculated from a thermogravimetric curve. Knowledge of the kinetic parameters associated with thermal degradation constitutes and important tool in estimating the thermal behavior of composites under dynamic conditions.
The purpose of this study is to evaluate the thermal stability of novel hybrid copolymers containing thermosensitive and polypeptide blocks, as well as to establish the most appropriate mechanism of the thermal degradation and to calculate the kinetic parameters characterizing this process.
2. Experimental Part
2.1. Materials and Measurements
The thermally sensitive macroinitiator PNIPAm-g-PEО and the corresponding polypeptide-based hybrid copolymer (PNIPAm-g-PEO)-b-PLys were synthesized according to a procedure described elsewhere [13]. Briefly, PNIPAm-g-PEО was synthesized through a radical copolymerization of NIPAm and poly(ethylene glycol) methacrylate (Mn ~ 500) in the presence of the chain-transfer reagent 2-aminoethanethiol. 1H NMR (CDCl3): d 4.00 (CH-(CH3)2); d 3.64 (O-CH2CH2-O); d 2.3 - 1.5 (CH2-CH + CH2-CH + CH2-C); d 1.24 (CH3-C); d 1.13 (CH3)2-CH). GPC in N,N’-dimethylformamide (vs. polystyrene standards): Mw/Mn = 1.65. Mn = 16400 – titration of the terminal primary amine groups. The hybrid copolymer, (PNIPAmg-PEO)-b-PLys was synthesized via ammonium-mediated ring-opening polymerization of Z-L-lysine-NCA, initiated by the PNIPAm-g-PEО macroinitiator. 1H NMR (DMSOd6):1H NMR (DMSO-d6): d 7.90 - 8.19 (aCH-NH); d 6.85 - 7.38 (aCH-(CH2)4-NH + NH-CH-(CH3)2 + C6H5); d 4.99 (Z-CH2); d 4.60 (OH); d 4.20 (aCH-NH); d 3.84 (CH- (CH3)2); d 3.52 (O-CH2CH2-O); d 2.94 (αCH-(CH2)3CH2); d 1.93 (CH2-CH); d 1.20 - 1.70 (CH3-C + CH2-CH + αCH- (CH2)3 + CH2-C); d 1.05 (CH-(CH3)2). GPC in N,N’-dimethylformamide (vs. polystyrene standards): Mw/Mn = 1.62. Finally, the Z-protecting groups were cleaved from the polypeptide block with HBr in trifluoroacetic acid. 1H NMR (D2O): d 4.28 (aCH-NH); d 3.87 (CH-(CH3)2); d 3.67 (O-CH2CH2-O); d 2.96 (αCH-(CH2)3CH2); d 1.39 - 2.10 (CH2-CH + αCH-(CH2)3 + CH2-CH); d 1.11 (CH- (CH3)2 + CH3-C).
The thermogravimetrical measurements (TG-DTGDTA) of these samples were carried out in a flow of nitrogen at a rate of 25 cm3·min–1 under non-isothermal conditions on an instrument STA 449 F3 Jupiter (Nietzsch, Germany) with its high temperature furnace. Samples of about 5 ± 0.1 mg mass were used for the experiments varied out at hearing rate of 6˚C min–1 up to 700˚C. The samples were loaded without pressing into an open 6 mm diameter and 3 mm high platinum crucible, without using of a standard reference material. The TG, DTG and DSC curves were recorded simultaneously with 0.1 mg sensitivity.
2.2. Theoretical Approach and Calculation Procedures
The kinetics of thermal degradation reactions is described by various equations taking into account the special features of their mechanisms. The reaction rate can be expressed through the degree of conversion a according to the formula:
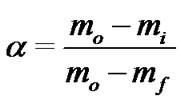 (1)
(1)
where: mo, mf and mi are initial, final and current sample mass at the moment t, respectively. Generally, the kinetic equation of the process can be written as follows [10- 12,14,15]:
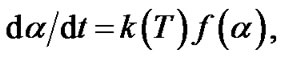 (2)
(2)
where f(a) is the conversion function and k(T) is the temperature function respectively. The temperature dependence of the rate constant k for the process is described by the Arrhenius equation:
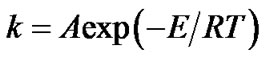 (3)
(3)
where A is the pre-exponential factor, T is the absolute temperature, R is the universal gas constant, and E is the apparent activation energy of the process. Substitution of Equation (3) in (2) gives:
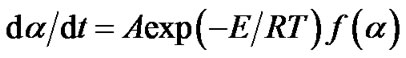 (4)
(4)
When the temperature increases at a constant rate,
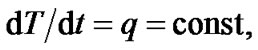 (5)
(5)
therefore
 (6)
(6)
The conversion function f(a) for a solid-state reaction depends on the reaction mechanism and can generally be considered to be as follows:
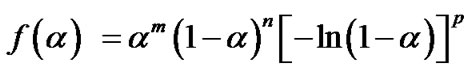 (7)
(7)
where m, n and p are empirically obtained exponent factors, one of them always being zero [15,16].
After substitution in Equation (6), separation of variables and integration, the following general equation was obtained
 (8)
(8)
The solutions of the left hand side integral depend on the explicit expression of the function f(a) and are denoted as g(a). Algebraic expressions of functions of the most common reaction mechanisms operating in solidstate reactions are summarized and presented in some papers [15,17-19].
The right-hand side integral or so called “temperature integral” in Equation (8) has no exact analytical solution. Coats and Redfern [23] suggested the calculation procedure based on next linear equation:
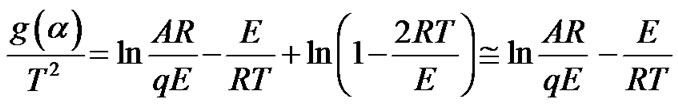 (9)
(9)
where g(a) is a function, the expression of which depends on the kinetic model of the occurring reaction. If the correct g(a) is used, a plot of ln[g(a)/T2] against 1/T should give a straight line from which the values of the activation energy E and the pre-exponential factor A in Arrhenius equation can be calculated. The formal expressions of the functions g(a) depend on the conversion mechanism and its mathematical model [10-12,15,17]. The latter usually represents the limiting stage of the reaction—the chemical reactions; random nucleation and nuclei growth; phase boundary reaction or diffusion. For the correct g(a) [15,17-19], the corresponding linear dependence should give the highest correlation coefficient at the linear regression analysis.
From the theory of the activated complex (transition state) of Eyring [10-12,15,20,21], it is known that:
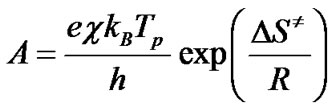 (10)
(10)
where е = 2.7183 is the Neper number; χ—transmission factor, which is unity for monomolecular reactions; kB— Boltzmann constant; h—Plank constant, and Tp is the peak temperature of the DTA curve. The change of entropy DS¹ may be calculated according to the formulae [11,15]
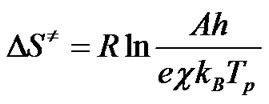 (11)
(11)
Since
 (12)
(12)
the changes of the enthalpy DH¹ and Gibbs free energy DG¹ for the activated complex formation from the reagent can be calculated using the well known thermodynamical equation [10-12,15,20,21]:
 (13)
(13)
The values of DS¹, DH¹ and DG¹ were calculated at T = Tp (Tp is the peak temperature at the corresponding stage), since this temperature characterizes the highest rate of the process, and therefore, is its important parameter [10- 12,15,20,21].
2.3. Estimation of Lifetime
Lifetime estimations are very useful in the development or selection of polymers for different applications. Lifetime is usually determined by accelerated aging, like air oven aging studies, which require long time periods. The apparent kinetic parameters calculated in the manner described above have been used to calculate the value of lifetime for hybrid copolymers. The estimated lifetime or the time accelerating ageing tf of hybrid copolymers to failure have been defined as the time when the mass loss reaches 5 mass%, i.e. a = 0.05 [21,22] and can be estimated by the following equation
 (14)
(14)
 (15)
(15)
where the value of the reaction order n has been obtained previously. With these equations, the time to equivalent damage at different temperatures can be calculated.
3. Results and Discussion
3.1. Copolymer Samples
Novel, self-associating hybrid copolymers containing thermosensitive and polypeptide blocks were synthesized via controlled ring-opening polymerization of NCA of Z-Llysine (Z-L-Lys-NCA), initiated by amino-functional macroinitiators [13].
A NIPAm and poly(ethylene glycol) methacrylate were radically copolymerized in the presence of chaintransfer reagent to obtain the thermally sensitive endfunctional macroinitiator PNIPAm-g-PEO (Figure 1(a)). The molar content of poly(ethylene glycol) side chains was estimated from the 1H NMR spectrum of the product, while the molar mass was determined from an acid-base titration of the amine end-groups. In the next step PNIPAm-g-PEO was used to initiate the ring-opening polymerization of Z-L-lysine. Knowing the macroinitiators’ molar mass and composition, the degree of peptide polymerization was estimated from the 1H NMR spectrum of the copolymer in DMSO-d6. The formation of block architecture was proved by GPC analyses in N,N’-dimethylformamide. The Z-protecting groups in the polypeptide block were cleaved under acid conditions to give the final product with a structure presented on Figure 1(b). To evaluate the thermal properties of the macroinitiator (PNIPAm-g-PEO) and (PNIPAm-g-PEO)-b-PZLLys copolymers, they were studied using the method of differential thermal analysis. The studies were made under a heating rate of 6˚C min–1 in inert medium. The registered curves are shown in Figures 2 and 3.
A two-stage mechanism of thermo-oxidative destructtion of the hybrid copolymer was observed: primary thermo-oxidative destruction of the of the thermally unstable fragments (grafted chains of PEO), and secondary thermo-oxidative destruction of the main polymer chains of poly(N-isopropylacrylamide) and poly(L-lysine). The thermogravimetrical curves exhibited a multi-step character, which is related to the different thermal stability of the polymer segments included in the hybrid copolymer. In both samples, macroinitiator and copolymer, dehydration was observed in the temperature interval of 60˚C - 140˚C, which is related to the dissociation of water molecules.
 (a)
(a)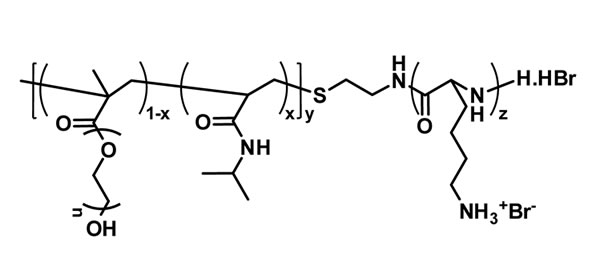 (b)
(b)
Figure 1. Structures of: (a) thermally sensitive macroinitiator PNIPAm-g-PEО; and (b) the corresponding polypeptidebased hybrid copolymer (PNIPAm-g-PEO)-b-Plys.

Figure 2. DTA, TGA and DSC curves for (PNIPAm-g-PEO).
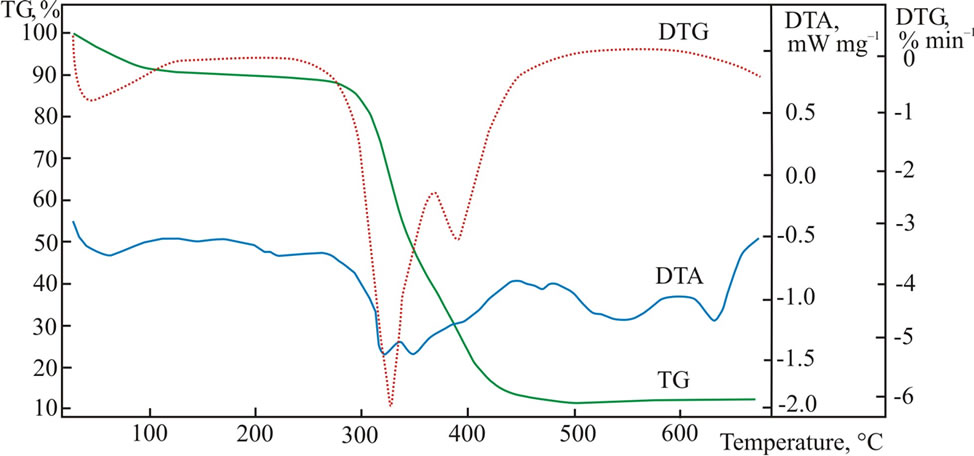
Figure 3. DTA, TGA and DSC curves for (PNIPAm-g-PEO)-b-PLLys.
This can be explained with the high hydrophilicity of the studied materials, which absorb water molecules even at room temperature. The maximum decomposition rate of the macroinitiator was registered at 402˚C and is related to the thermal destruction of the PEO and PNIPAm segments. The hybrid copolymer had two distinctly marked maximum rates, at 326˚C and 391˚C, which are probably related to the destruction of the PEO and PNI-PAm chains and the polylysine polypeptide block. The thermal curves showed that there were no visible changes in the structure of the studied materials when heated up to 270˚C.
3.2. Kinetic Studies
Using the calculation procedures of Coats and Redfern [23], all g(a) functions presented in some paper [10-12, 14,15] were first substituted into Equation (9) and the plot of the left side of this equation against 1/T was fitted by computer to calculate the correlation coefficient of linear regression R2. This procedure was repeated until the best R2 value was obtained. For the thermal degradation of the samples studied, single heating rate plots, ln[g(a)/T2] against 1/T, were calculated according to Equation (9). It should be noted for all the samples studied that the highest values of R2 were obtained when kinetic equations for the Fn mechanism with different values of n were used. In this respect, the kinetic curves of thermal degradation of (PNIPAm-g-PEO) with different values of n are presented in Figure 4 for illustration.
Figure 4 shows that the shapes of the kinetic curves strongly depend on the value of the parameter n. To find the value of n with which the highest value of R2 is obtained, the dependence R2 = f(n) was drawn and is presented in Figure 5.
The curve presented in Figure 5 can be described well with empiric polynoms of second order. Differentiating these polynoms vs. n and assuming their value to be null, the value of n at which R2 has maximum value could be calculated. For (PNIPAm-g-PEO) the maximum of R2 was obtained at n = 1.0. Similar calculations were carried out for hybrid copolymer. The results showed that the best linear correlations for all studied samples were obtained using the mechanism non-invoking equation (Fn). To find the value of n with which the highest value of R2 is obtained, the dependence R2 = f(n) was drawn for both stages and is presented in Figure 6.
As can be seen from Figure 6, for the first stage, the maximum of R2 was obtained at n = 0.333, and for the second stage—at n = 2.3. Subsequently, the apparent activation energy E and the pre-exponential factor A can be calculated from the slope and intercept of the fitted straight line. Using Equations (11)-(13), the values of the change of entropy ΔS≠, enthalpy ΔH≠ and the Gibbs free energy ΔG≠ for the formation of the activated complex from the reagent were defined. The results obtained are summarized in Table 1.
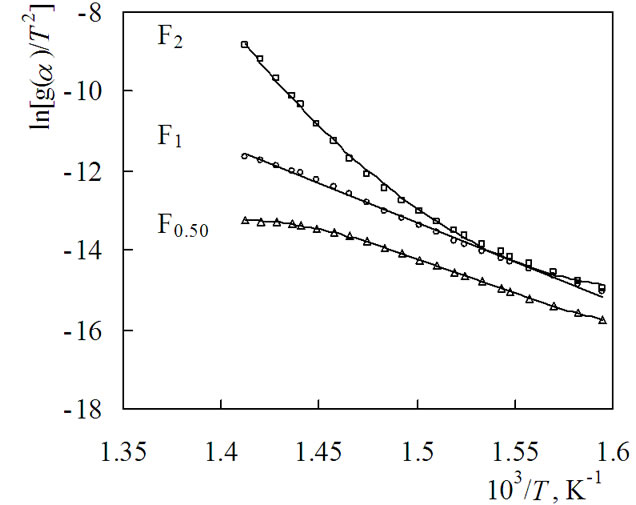
Figure 4. Dependence of ln[g(a)/T2] vs. 1/T of (PNIPAm-gPEO) according to Coats-Redfern calculation procedure for different values of n, drawn using mechanism non-invoking equations.
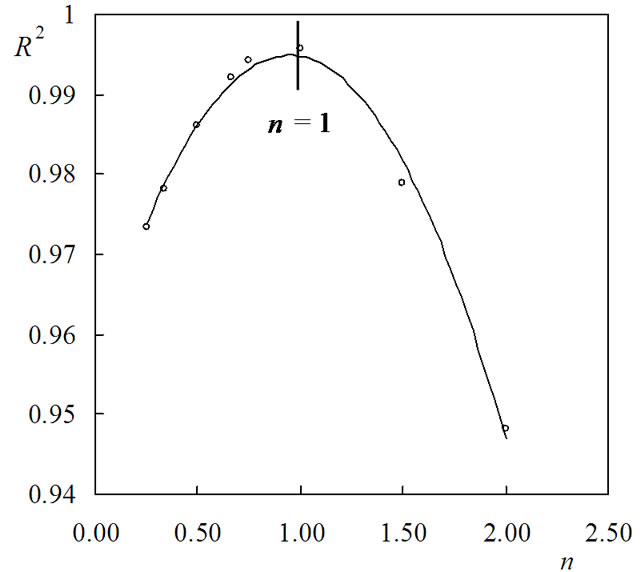
Figure 5. Dependence of the coefficient of linear regression R2 on the values of n for thermal degradation of (PNIPAmg-PEO).
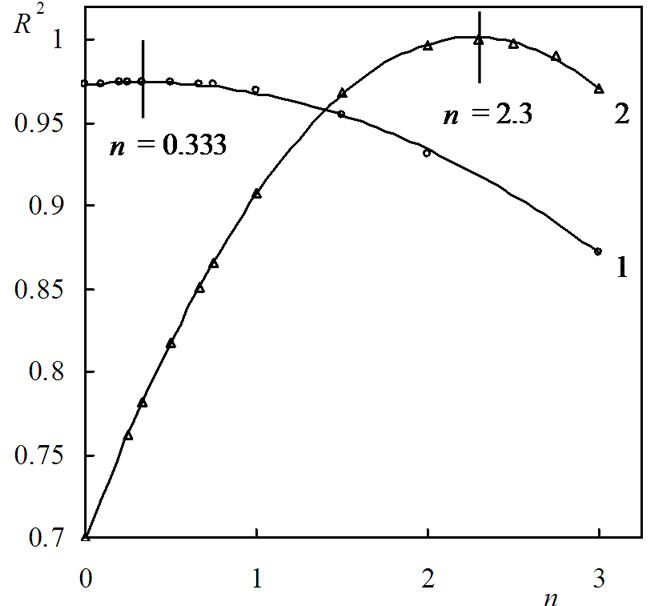
Figure 6. Dependence of the coefficient of linear regression R2 on the values of n for thermal degradation of (PNIPAm-gPEO)-b-PLLys: 1: first stage and 2: second stage.
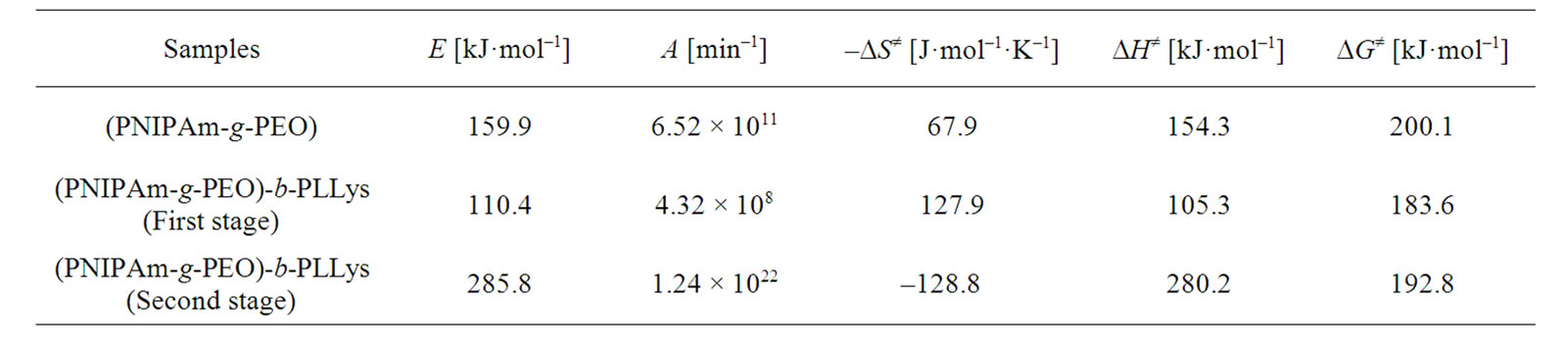
Table 1. Kinetic parameter of thermal degradation of (PNIPAm-g-PEO) and (PNIPAm-g-PEO)-b-PLLys.
As can be seen from Table 1, the highest values were observed for the second stage of the hybrid copolymer. The values of the pre-exponential factor for a solid phase reactions are expected to be in a wide range (six or seven orders of magnitude), even after the effect of surface area is taken into account [24]. For first order reactions, the pre-exponential factor may vary from 105 to 1016 min–1.
The low factors will often indicate a surface reaction, but if the reactions are not dependent on surface area, the low factor may indicate a “tight” complex. The high factors will usually indicate a “loose” complex [25]. Even higher factors (after correction for surface area) can be obtained for complexes having free translation on the surface. Since the concentrations in solids are not controllable in many cases, it would have been convenient if the magnitude of the preexponential factor indicated for reaction molecularity. However, this appears to be true only for non-surface-controlled reactions having low (<108 min–1) pre-exponential factors. Such reactions (if elementary) can only be bimolecular.
The change of Gibbs free energy DG¹ reflects the total energy increase of the system at the approach of the reagents and the formation of the activated complex. This energy is influenced by two thermodynamic properties, the changes of enthalpy DH¹ and entropy DS¹ of activated complex formation. The change of activation enthalpy shows the energy differences between the activated complex and the reagents. If this difference is small, the formation of activated complex is favored, because the potential energy barrier is low. The change of reaction entropy reflects how near the system is to its own thermodynamic equilibrium. Low activation entropy means that the material has just passed through some kind of physiccal or chemical aging process, bringing it to a state near its own thermodynamic equilibrium. In this situation, the material shows little reactivity, increasing the time taken to form the activated complex. On the other hand, when high activation entropy values are observed, the material is far from its own thermodynamic equilibrium. In this case, the reactivity is high and the system can react faster to produce the activated complex, which resulted in the short reaction times observed [24,26].
The curves representing the dependence of lifetime on the temperature at 5% conversion for both stages of thermal degradation of (PNIPAm-g-PEO)-b-PLLys and (PNIPAm-g-PEO) are shown in Figure 7.
It is obvious from Figure 7 that the lifetime is a parameter strongly depending on the temperature and decreases exponentially with the increase of the temperature. The lifetime is more sensitive concerning the temperature for the second stage of the thermal decomposition of hybrid copolymer.
4. Conclusions
The thermal degradation kinetics of hybrid copolymers with thermally sensitive and polypeptide segments was analyzed using Coats-Redfern calculation procedure and 27 model kinetic equations. The kinetic parameters E, A, DS¹, DH¹ and DG¹ for studied samples were calculated. The main results obtained in this article were summarized as follows.
1) The kinetic of non-isothermal degradation of the samples studied was best described by non-invoking mechanism equations with nth order (Fn mechanism).
2) Depending on the structure of the samples used the values of n varied from 0.333 to 2.3.
3) The highest values of n, Е and A were observed for the second stage of thermal degradation of (PNI-PAmg-PEO)-b-PLLys.
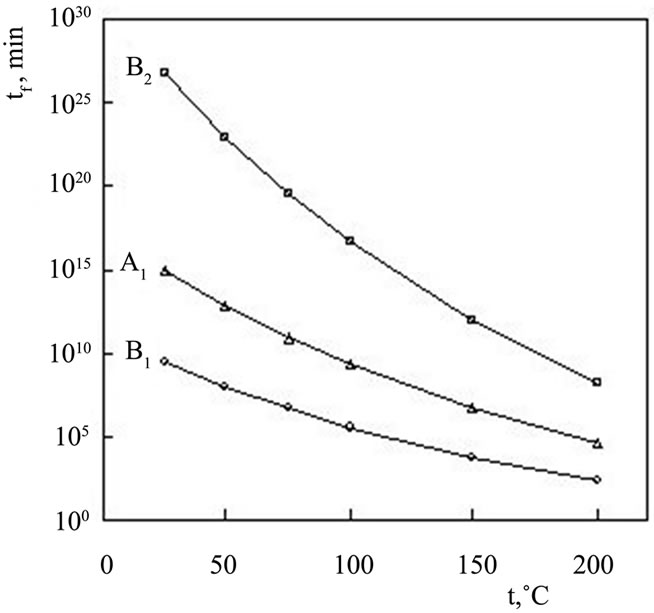
Figure 7. Results for lifetime as a function of service temperature in synthetic air for: A1: (PNIPAm-g-PEO); B1: first stage; and B2: second stage of thermal degradation of (PNIPAm-g-PEO)-b-PLLys.
4) Results for lifetime as a function of service temperature in nitrogen for the samples (PNIPAm-g-PEO)-b-PLLys show that the lifetime is more sensitive concerning the temperature for the second stage of the thermal decomposition of hybrid copolymer.
5) It was established that these novel hybrid block copolymers possess a good thermal stability in the temperature interval up to 270˚C and can be successfully used as polymer carriers in systems for targeted drug delivery.
5. Acknowledgements
The authors would like to express their gratitude to Operating Programme Human Resources Development; Grant agreement: BG051PO001/3.3-05-001 “Science and Business” Funded by: EC, European Social Fund for their financial support.
REFERENCES
- I. Dimitrov and H. Schlaad, “Synthesis of Nearly Monodisperse Polystyrene-Polypeptide Block Copolymers via Polymerisation of N-Carboxyanhydrides,” Chemical Communications, No. 23, 2003, pp. 2944-2945. doi:10.1039/b308990h
- T. J. Deming, “Polypeptide and Polypeptide Hybrid Copolymer Synthesis via NCA Polymerization,” Advances in Polymer Science, Vol. 202, 2006, pp. 1-18. doi:10.1007/12_080
- I. Dimitrov and I. Berlinova, “Synthesis of Poly(Ethylene Oxide)s Bearing Functional Groups along the Chain,” Macromolecular Rapid Communications, Vol. 24, No. 9, 2003, pp. 551-555. doi:10.1002/marc.200390086
- J. Jagur-Grodzinski, “Preparation of Functionalized Polymers Using Living and Controlled Polymerizations,” Reactive and Functional Polymers, Vol. 49, No. 1, 2001, pp. 1-54. doi:10.1016/S1381-5148(01)00059-1
- I. Dimitrov, I. Berlinova and N. Vladimirov, “Synthesis of Poly(oxyethylene)-Poly(Z-L-lyzine) Hybrid Graft Copolymers,” Macromolecules, Vol. 39, No. 6, 2006, pp. 2423-2426. doi:10.1021/ma0524981
- I. Berlinova, I. Dimitrov, R. Kalinova and N. Vladimirov, “Synthesis and Aqueous Solution Behaviour of Copolymers Containing Sulfobetaine Moieties in Side Chains,” Polymer, Vol. 41, No. 3, 2000, pp. 831-837. doi:10.1016/S0032-3861(99)00264-5
- A. Hirao and M. Hayashi, “Recent Advance in Syntheses and Applications of Well-Defined End-Functionalized Polymers by Means of Anionic Living Polymerization,” Acta Polymerica, Vol. 50, No. 7, 1999, pp. 219-231. doi:10.1002/(SICI)1521-4044(19990701)50:7<219::AID-APOL219>3.0.CO;2-U
- I. Berlinova, A. Nedelcheva, V. Samichkov and Ya. Ivanov, “Thermally Induced Hydrogel Formation in Aqueous Solutions of Poly(N-isopropylacrylamide) and FluorocarbonModified Poly(oxyethylene)s,” Polymer, Vol. 43, No. 26, 2002, pp. 7243-7250. doi:10.1016/S0032-3861(02)00678-X
- F. Meng, Z. Zhong and J. Feijen, “Stimuli-Responsive Polymersomes for Programmed Drug Delivery,” Biomacromolecules, Vol. 10, No. 2, 2009, pp. 197-209. doi:10.1021/bm801127d
- V. Georgieva, D. Zvezdova and L. Vlaev, “Non-Isothermal Kinetics of Thermal Degradation of Chitin,” Journal of Thermal Analysis and Calorimetry, 2012, in Press. doi:10.1007/s10973-012-2359-6
- R. Bigda and A. Mianowski, “Influence of Heating Rate on Kinetic Quantities of Solid Phase Thermal Decomposition,” Journal of Thermal Analysis and Calorimetry, Vol. 84, No. 2, 2006, pp. 453-465. doi:10.1007/s10973-005-7378-0
- C. L. Albano, E. S. Sciamanna, T. Aquno and J. J. Martinez, “Metodology to Evaluate Thermogravimetric Data Using Computational Techniques in the Polymer Field,” European Congress on Computational Methods in Applied Science and Engineering, Barcelona, 11-14 September 2000.
- E. Ivanova, I. Dimitrov, R. Kozarova, S. Turmanova and M. Apostolova, “Thermally Sensitive Polypeptide-Based Copolymers for DNA Complexation into Stable Nanosized Polyplexes,” Nano Research, 2012, Submitted.
- A. Cadenato, J. M. Morancho, X. Fernandez-Francos, J. M. Salla and X. Ramis, “Comparative Kinetic Study of the Non-Isothermal Curing of Bis-GMA/TEGDMA Systems,” Journal of Thermal Analysis and Calorimetry, Vol. 89, No. 1, 2007, pp. 233-244. doi:10.1007/s10973-006-7567-5
- L. T. Vlaev, V. G. Georgieva and S. D. Genieva, “Products and Kinetics of Non-Isothermal Decomposition of Vanadium(IV) Oxide Compounds,” Journal of Thermal Analysis and Calorimetry, Vol. 88, No. 3, 2007, pp. 805-812. doi:10.1007/s10973-005-7149-y
- J. Šestak and G. Berggren, “Study of the Kinetics of the Mechanism of Solid-State Reactions at Increasing Temperatures,” Thermochimica Acta, Vol. 3, 1971, pp. 1-12. doi:10.1016/0040-6031(71)85051-7
- Y. Chen and Q. Wang, “Thermal Oxidative Degradation Kinetics of Flame-Treated Polypropylene with Intumescent Flame-Retardant Master Batches in Situ Prepared in Twin-Screw Extruder,” Polymer Degradation and Stability, Vol. 92, No. 2, 2007, pp. 280-291. doi:10.1016/j.polymdegradstab.2006.11.004
- S. M. Lomakin, L. L. Dubnikova, S. M. Berezina and G. E. Zaikov, “Kinetic Study of Polypropylene Nanocomposite Thermo-Oxidative Degradation,” Polymer International, Vol. 54, No. 7, 2005, pp. 999-1006. doi:10.1002/pi.1795
- X. Ramis, A. Cadenato, J. M. Salla, J. M. Morancho, A. Valles, L. Contat and A. Ribes, “Thermal Degradation of Polypropylene/Starch-Based Materials with Enhanced Biodegradability,” Polymer Degradation and Stability, Vol. 86, No. 3, 2004, pp. 483-491. doi:10.1016/j.polymdegradstab.2004.05.021
- B. Boonchom and M. Thongkam, “Kinetics and Thermodynamics of the Formation of MnFeP4O12,” Journal of Chemical & Engineering Data, Vol. 55, No. 1, 2010, pp. 211-216. doi:10.1021/je900310m
- W. He, F. Deng, G. X. Liao, W. Lin, Y. Y. Jiang and X. G. Jian, “Kinetics of Thermal Degradation of Poly(aryl ether) Containing Phthalazinone and Life Estimation,” Journal of Thermal Analysis and Calorimetry, Vol. 100, No. 3, 2010, pp. 1055-1062. doi:10.1007/s10973-009-0515-4
- H. Wang, X. Tao and E. Newton, “Thermal Degradation Kinetics and Lifetime Prediction of a Luminescent Conducting Polymer,” Polymer International, Vol. 53, No. 1, 2004, pp. 20-26. doi:10.1002/pi.1279
- W. Coats and J. P. Redfern, “Kinetic Parameters for Thermogravimetric Data,” Nature, Vol. 201, No. 4914, 1964, pp. 68-69. doi:10.1038/201068a0
- S. Ch. Turmanova, S. D. Genieva, A. S. Dimitrova and L. T. Vlaev, “Non-Isothermal Degradation Kinetics of Filled with Rice Husk Ash Polypropene Composites,” Express Polymer Letters, Vol. 2, No. 2, 2008, pp. 133-146. doi:10.3144/expresspolymlett.2008.18
- L. Vlaev, N. Nedelchev, K. Gyurova and M. Zagorcheva, “A Comparative Study of Non-Isothermal Kinetics of Decomposition of Calcium Oxalate Monohydrate,” Journal of Analytical and Applied Pyrolysis, Vol. 81, No. 2, 2008, pp. 253-262. doi:10.1016/j.jaap.2007.12.003
- A. Ruvolo-Filho and P. S. Curti, “Chemical Kinetic Model and Thermodynamic Compensation Effect of Alkaline Hydrolysis of Waste Poly(ethylene terepftalate) in Nonaqueous Ethylene Glycol Solution,” Industrial & Engineering Chemistry Research, Vol. 45, No. 24, 2006, pp. 7985-7996. doi:10.1021/ie060528y
NOTES
*Corresponding author.

