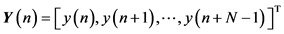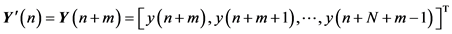Journal of Power and Energy Engineering
Vol.05 No.09(2017), Article ID:78853,13 pages
10.4236/jpee.2017.59001
A Tunable Resolution MUSIC Algorithm for Interharmonics Analysis
Ming Zhang1*, Xiang Zhang1, Heng Yao1, Shunfan He2
1School of Electronic and Electrical Engineering, Wuhan Textile University, Wuhan, China
2College of Computer Science, South Central University for Nationalities, Wuhan, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 27, 2017; Accepted: August 28, 2017; Published: August 31, 2017
ABSTRACT
The harmonic and interharmonic analysis recommendations are contained in the latest IEC standards on power quality. Measurement and analysis experiences have shown that great difficulties arise in the interharmonic detection and measurement with acceptable levels of accuracy. In order to improve the resolution of spectrum analysis, the traditional method (e.g. discrete Fourier transform) is to take more sampling cycles, e.g. 10 sampling cycles corresponding to the spectrum interval of 5 Hz while the fundamental frequency is 50 Hz. However, this method is not suitable to the interharmonic measurement, because the frequencies of interharmonic components are non-integer multiples of the fundamental frequency, which makes the measurement additionally difficult. In this paper, the tunable resolution multiple signal classification (TRMUSIC) algorithm is presented, which the spectrum can be tuned to exhibit high resolution in targeted regions. Some simulation examples show that the resolution for two adjacent frequency components is usually sufficient to measure interharmonics in power systems with acceptable computation time. The proposed method is also suited to analyze interharmonics when there exists an undesirable asynchronous deviation and additive white noise.
Keywords:
Interharmonics Analysis, Tunable Resolution Multiple Signal Classification (TRMUSIC) Algorithm, Subspace Decomposition, Spectral Analysis

1. Introduction
Interharmonics can be thought of as the inter-modulation of the fundamental and harmonic components of the power system with any other frequency components and can be observed in an increasing number of loads. These loads include static frequency converters, cycloconverters, sub-synchronous converter cascades, induction motors, arc furnaces and so on [1] .
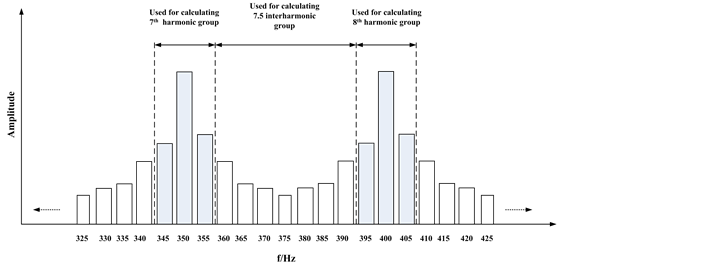
A method, which is aimed to standardize the harmonic and interharmonic measurement, has been proposed by the IEC [2] . This method utilizes discrete Fourier transform (DFT) performed over a rectangular time window of exactly 10 cycles for 50 Hz power systems. The window width fixes the frequency resolution at 5 Hz, so the interharmonic components that are between the bins spaced of 5 Hz would spill over primarily into adjacent interharmonic bins with a minimum of spill into harmonic bins. Therefore, the harmonic and interharmonic groups are introduced. The interharmonic group is defined as the RMS (Root- mean-square) value of all the interharmonic components between adjacent harmonic groups (see Figure 1).
However, the accurate estimation method of the interharmonic components has not been established yet. Many researchers have been studying new methods. For analyzing a range of the interharmonic components, researchers often use DFT and its improved algorithms to calculate amplitudes, frequencies and phases of the interharmonic components [3] [4] [5] [6] [7] . The major pitfalls in the common DFT applications are the spectral leakage and picket fence effects.
The multiple signal classification (MUSIC) algorithm exploits the noise subspace to estimate the unknown parameters of the random process, which was proposed by R. O., Schmidt [8] . This algorithm can also estimate the frequencies of complex sinusoids corrupted with additive white noise. T. Lobos et al. [9] [10] have already proposed the frequencies determination method of the harmonic components using the MUSIC algorithm. But it is difficult to estimate the frequencies of the interharmonic components.
In this paper, the tunable resolution MUSIC (TRMUSIC) algorithm is presented to estimate the parameters of interharmonics, which the spectrum can be tuned to exhibit high resolution in targeted regions. The organization of this paper is as follows. The interharmonic measurement method based on the TRMUSIC algorithm is proposed in Section 2. Then, simulation results to demonstrate the
Figure 1. Harmonic and interharmonic (sub) groups.
validity, precision feasibility and robustness of the algorithm are presented in Section 3. At last, the conclusions are given in Section 4.
2. Trmusic Algorithm
2.1. Music Algorithm
The MUSIC algorithm is an eigenvalue subspace decomposition method for estimation of the frequencies of complex sinusoids observed in additive white noise. Consider a noisy signal vector 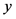 comprised of
comprised of  complex sinusoids modeled as
complex sinusoids modeled as
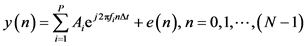 (1)
(1)
with
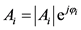 (2)
(2)
where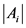 ,
, 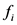 and
and  represent the amplitude, frequency and phase of i-th complex sinusoid, respectively.
represent the amplitude, frequency and phase of i-th complex sinusoid, respectively.  is the number of samples in one data rectangular window,
is the number of samples in one data rectangular window,  is the fixed time interval, and
is the fixed time interval, and  is a zero mean Gaussian white noise vector with variance
is a zero mean Gaussian white noise vector with variance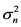 .
.
Suppose that  is the sampled set. Since it is known that
is the sampled set. Since it is known that 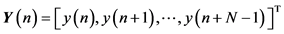 , the
, the 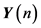 can be expressed as
can be expressed as
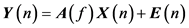 (3)
(3)
with
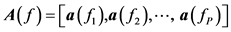 (4)
(4)
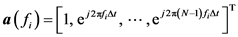 (5)
(5)
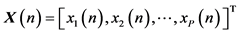
where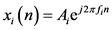
The auto-correlation matrix of the noisy signal 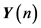

where 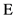
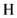
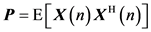
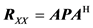
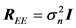
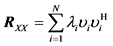
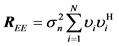
where 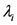
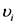

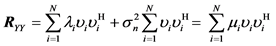
where 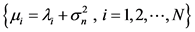
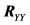
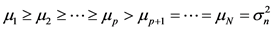
Furthermore, the singular value decomposition (SVD) of the matrix 
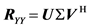
where the columns of 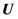
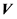



Then, the MUSIC spectrum is defined as [11]

with
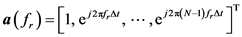
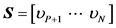
where 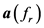
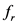
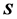
2.2. The Proposed Tunable Resolution Method
The frequency resolution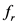
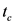
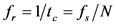

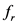
Here, a method of obtaining spectral interpolation data on the use of tunable factor 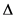
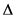
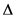
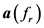

with

where 
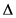
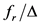
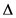
2.3. Denouncing Algorithm Based on Cross-Spectral Estimation
The most important step is to estimate the signal subspace dimension 
Assume two signal sequences
then

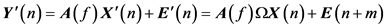
with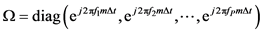
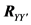
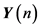

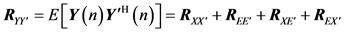
From Equation (20), the matrix 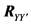

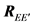
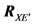
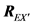
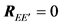

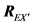
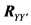

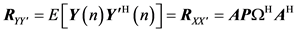
where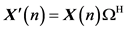
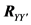
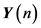
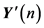
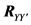
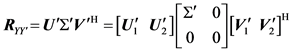
Figure 2. Resolution of MUSIC spectrum.
where the columns of 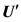
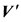
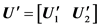
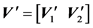
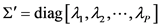
In a real application, the cross-correlation matrix 
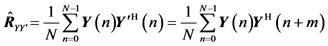
The matrix 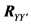

where each element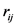
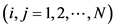
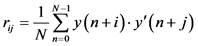
So, the Equation (23) can be used to estimate the signal subspace dimension 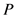
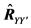
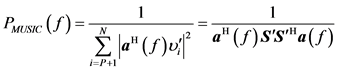
where 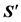
2.4. Estimation Method of the Amplitude and Phase of the Harmonic and Interharmonic Components
The frequencies of the harmonic and interharmonic components can be estimated from the peak location of the MUSIC spectrum, i.e., the frequencies 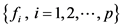

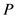
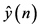
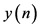
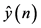
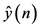
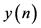

where

Equation (27) can be used to solve least squares for the coefficients 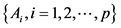
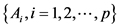
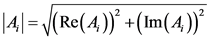
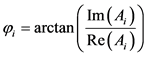
where 

3. Simulation Results
Three cases are performed in Matlab to demonstrate the effectiveness of the proposed algorithm.
3.1. Case 1
In practice, the fundamental frequency often deviates from its nominal value. In the first simulation, the fundamental frequency is set to 49 Hz, and the signal is
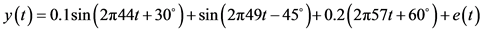
the sampling frequency 
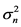
In the second simulation, the fundamental frequencies is set to 50.2 Hz, and the signal is
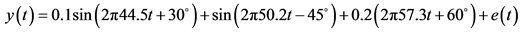
the sampling frequency 

In Figure 3 and Figure 4, the results demonstrate that the TRMUSIC algorithm is not affected by asynchronous sampling, while the MUSIC algorithm performs badly in that the peaks of the MUSIC spectrum are not sharp, and the DFT algorithm produces large spectral leakage and it even cannot detect most of the true frequencies of components in the signal. For example, the second simulation requires that the best frequency resolution is 0.1 Hz, however, the frequency resolution of the MUSIC and DFT algorithm is 5 Hz, respectively. When
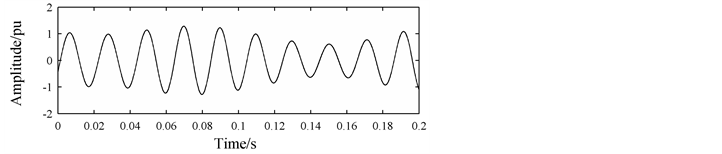
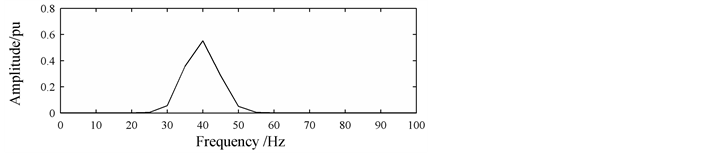
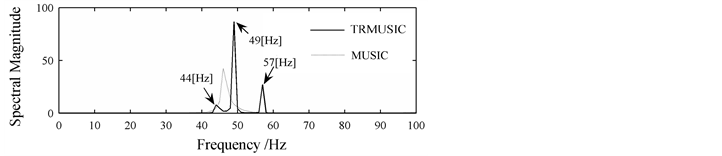
Figure 3. Spectrums of DFT, MUSIC and TRMUSIC algorithm for the first simulation: (a) Original signal; (b) DFT spectrum; (c) MUSIC and TRMUSIC spectrum.
the tunable factor 
3.2. Case 2
In this section, simulations are presented to demonstrate the anti-noise performance of TRMUSIC algorithm based on cross-spectral estimation comparing to that of the MUSIC algorithm based on auto-spectral estimation. When the signal represented by Equation (31) is contaminated with additive noise (SNR = 10 dB), the results of four simulations are shown in Figure 5. It can be seen that the TRMUSIC algorithm based on cross-spectral estimation is only slightly affected by additive noise because the pseudo-peaks can locate steadily in the corresponding frequency bins. Although the TRMUSIC spectrums are variable in the magnitudes, the estimation results are quite accurate. Therefore, the TRMUSIC algorithm based on cross-spectral estimation has satisfying results in analyzing noise- smeared signals.
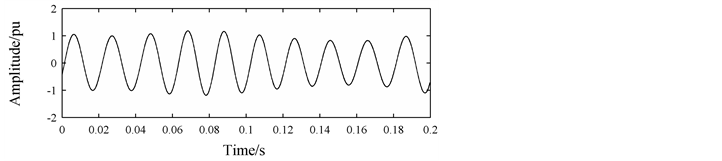
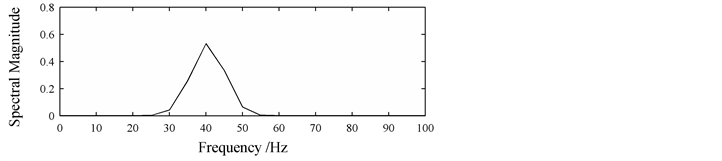

Figure 4. Spectrums of DFT, MUSIC and TRMUSIC algorithm for the second simulation: (a) Original signal; (b) DFT spectrum; (c) MUSIC and TRMUSIC spectrum.
Table 1. Results of fundamental and interharmonic components measurement.
In contrast, the MUSIC algorithm based on auto-spectral estimation has large errors of the signal subspace dimension 
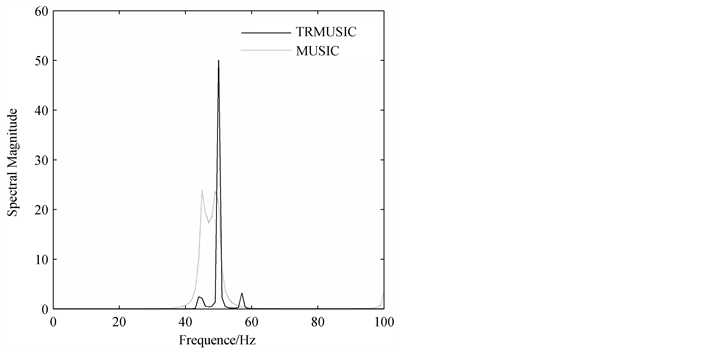
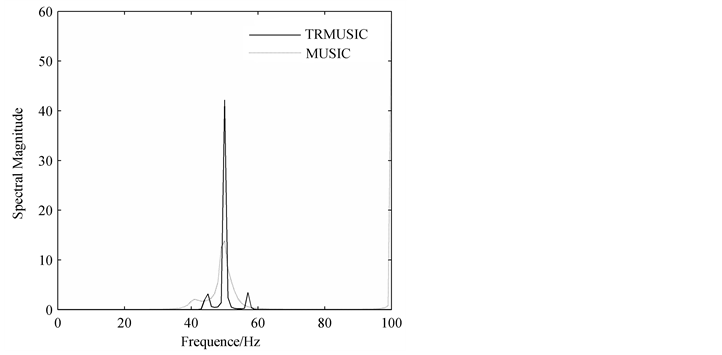
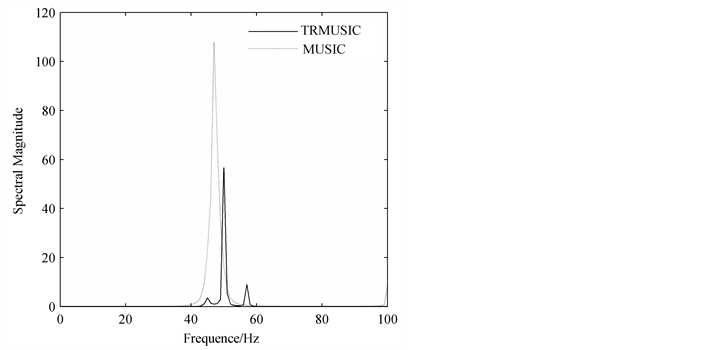
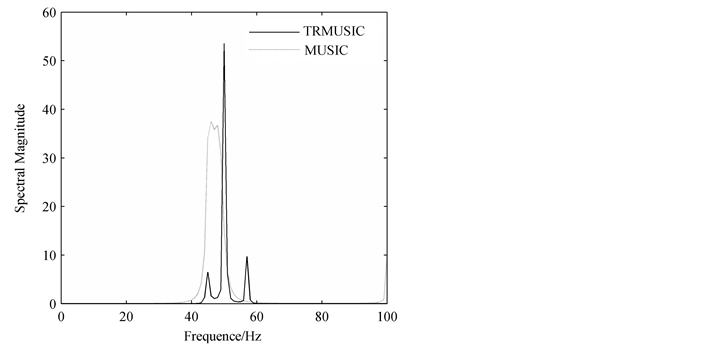
Figure 5. Comparison between the auto-spectral and cross-spectral estimation algorithm: (a) Simulation 1; (b) Simulation 2; (c) Simulation 3; (d) Simulation 4.
3.3. Case 3
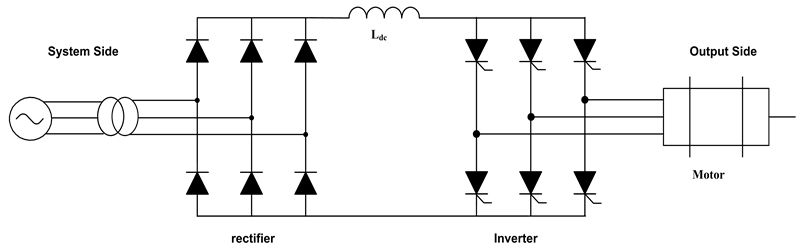
This simulation analyzes the harmonics in the AC/DC/AC converter system.
The AC/DC/AC converter system is a typical source of interharmonics [7] [15] . The inter-harmonic frequencies of the input current derive from the modulation of the converter harmonic components of operated by the rectifier harmonics (see Figure 6). The simulation model of the AC/DC/AC converter system is established in Matlab/Simulation. The parameters of the model are as follows. The parameters of the ac supply are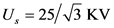

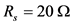
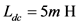
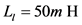
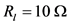
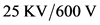
Figure 6. AC/DC/AC converter system.
Y-Y connection. The fundamental frequencies of system side and output side are 50 Hz and 60 Hz, respectively.
Figure 7 shows the interharmonics analysis results of current wave of phase B of the supply system side (5 cycles of samples). The components in the signal are measured by the TRMUSIC algorithm, which the tunable factor 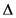
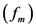
Then, the results of the TRMUSIC algorithm are compared with that of the MUSIC and DFT algorithm. For this simulation, we can see that the frequency analysis precision of the TRMUSIC algorithm is higher than that of the MUSIC and DFT algorithm, because the frequency resolution of the MUSIC and DFT algorithm is 10 Hz while that of TRMUSIC algorithm is 1 Hz, respectively. In Figure 7, when the frequencies don’t locate closest to the value of the integer frequency, the estimations with the TRMUSIC algorithm are quite accurate by predetermining the proper tunable factor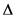
3.4. Comparison with MUSIC and DFT Algorithm
If fast Fourier transform (FFT) algorithm is used to compute its DFT, one such limitation is the power-of-two rule, requiring the number of input samples to be an integer power of two (i.e., 128, 256, 512). Therefore, choosing to lower sampling frequencies for better resolution is no longer a viable option. A clever engineer would simply increase the number of samples being taken. However, this solution quickly gets out of hand. In spite of this, the TRMUSIC algorithm may never be faster than the DFT algorithm.




Figure 7. Interharmonics analysis of 50 - 60 Hz AC/DC/AC converter system: (a) Current wave of phase B in system side; (b) DFT spectrum; (c) MUSIC spectrum; (d) TRMUSIC spectrum.
Compared to the traditional MUSIC algorithm, the TRMUSIC algorithm is much more flexible. Given the required frequency resolution of interharmonic analysis, you can choose the proper tunable factor
4. Conclusions
This paper proposes an effective method to estimate the parameters of interharmonics in power systems. With the increase of points in time domain, the frequency resolution is improved because the frequency resolution of MUSIC algorithm is 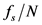
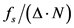
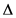
This research is very fundamental as an application to interharmonic analysis. Many tests were made in this work and the TRMUSIC algorithm is the most suitable to be used when estimating interharmonic spectrum. It gives us a handy solution for some drawbacks that can be found in methods like the DFT or traditional MUSIC algorithm.
The TRMUSIC algorithm really meets the need of offline applications. Furthermore, if this algorithm can be implemented in parallel computation, it should meet the need of online applications and be more practical.
Acknowledgements
This work is supported by National Natural Science Foundation of China (No. 51477124).
Cite this paper
Zhang, M., Zhang, X., Yao, H. and He, S.F. (2017) A Tunable Resolution MUSIC Algorithm for Interharmonics Analysis. Journal of Power and Energy Engineering, 5, 1-13. https://doi.org/10.4236/jpee.2017.59001
References
- 1. IEEE (1992) IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power Systems. IEEE, New York.
- 2. IEC (2002) General Guide on Harmonics and Interharmonics Measurements and Instrumentation for Power Supply Systems and Equipment Connected Thereto. IEC, Geneva.
- 3. Edison, B. and Alpine, M. (2016) An Evaluation of the Extent of Correlation between Inter-Harmonic and Voltage Fluctuation Measurements. IEEE Transactions on Power Delivery, 31, 753-760. https://doi.org/10.1109/TPWRD.2015.2480715
- 4. Lin, H.C. (2016) Identification of Interharmonics Using Disperse Energy Distribution Algorithm for Flicker Troubleshooting. IET Science, Measurement & Technology, 10, 786-794. https://doi.org/10.1049/iet-smt.2016.0110
- 5. Sun, Z., He, Z., Bang, T. and Li, Y. (2016) Multi-Interharmonic Spectrum Separation and Measurement under Asynchronous Sampling Condition. IEEE Transactions on Instrumentation and Measurement, 65, 1902-1912. https://doi.org/10.1109/TIM.2016.2562278
- 6. Chen, C. and Chen, Y. (2014) Comparative Study of Harmonic and Interharmonic Estimation Methods for Stationary and Time-Varying Signals. IEEE Transactions on Industrial Electronics, 61, 397-404. https://doi.org/10.1109/TIE.2013.2242419
- 7. Hui, J., Yang, H., Bu, W. and Li, Y. (2012) A Method to Improve the Interharmonic Grouping Scheme Adopted by IEC Standard 61000-4-7. IEEE Transactions on Power Delivery, 27, 971-979. https://doi.org/10.1109/TPWRD.2012.2183394
- 8. Schmidt, R.O. (1986) Multiple Emitter Location and Signal Parameter Estimation. IEEE Transactions on Antennas and Propagation, 34, 276-280. https://doi.org/10.1109/TAP.1986.1143830
- 9. Lobos, T., Napoleonic, Z., Reamer, J. and Schemer, P. (2000) High-Resolution Spectrum-Estimation Methods for Signal Analysis in Power Systems. IEEE Transactions on Instrumentation and Measurement, 55, 219-225. https://doi.org/10.1109/TIM.2005.862015
- 10. Leonowicz, Z., Lobos, T. and Rezmer, J. (2003) Advanced Spectrum Estimation Methods for Signal Analysis in Power Electronics. IEEE Transactions on Industrial Electronics, 50, 514-519. https://doi.org/10.1109/TIE.2003.812361
- 11. Kaveh, M. and Barabell, A.J. (1986) The Statistical Performance of the MUSIC and the Minimum-Norm Algorithms in Resolving Plane Waves in Noise. IEEE Transactions on Acoustics, Speech and Signal Processing, 34, 331-341. https://doi.org/10.1109/TASSP.1986.1164815
- 12. Pisarenko, V. (1973) The Retrieval of Harmonics from a Covariance Function. Geophysical Journal of the Royal Astronomical Society, 33, 347-366. https://doi.org/10.1111/j.1365-246X.1973.tb03424.x
- 13. Gu, J.F. and Wei, P. (2007) Joint SVD of Two Cross-Correlation Matrices to Achieve Automatic Pairing in 2-DAngle Estimation Problems. IEEE Antennas & Wireless Propagation Letters, 6, 553-556. https://doi.org/10.1109/LAWP.2007.907913
- 14. Hasan, M.K., Fattah, S.A. and Khan, M.R. (2003) Identification of Noisy AR Systems Using Damped Sinusoidal Model of Auto-Correlation Function. IEEE Signal Processing Letters, 10, 157-160. https://doi.org/10.1109/LSP.2003.811590
- 15. Li, C., Xu, W. and Tayjasanant, T. (2003) Interharmonics: Basic Concepts and Techniques for Their Detection and Measurement. Electric Power Systems Research, 66, 39-48. https://doi.org/10.1016/S0378-7796(03)00070-1