Received 7 October 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT

Modern electric power grids face a variety of new challenges and there is an urgent need to improve grid resilience more than ever before. The best approach would be to focus primarily on the grid intelligence rather than implementing redundant preventive measures. This paper presents the foundation for an intelligent operational strategy so as to enable the grid to assess its current dynamic state instantaneously. Traditional forms of real-time power system security assessment consist mainly of methods based on power flow analyses and hence, are static in nature. For dynamic security assessment, it is necessary to carry out time-domain simulations (TDS) that are computationally too involved to be performed in real-time. The paper employs machine learning (ML) techniques for real-time assessment of grid resiliency. ML techniques have the capability to organize large amounts of data gathered from such time-domain simulations and thereby extract useful information in order to better assess the system security instantaneously. Further, this paper develops an approach to show that a few operating points of the system called as landmark points contain enough information to capture the nonlinear dynamics present in the system. The proposed approach shows improvement in comparison to the case without landmark points.

Keywords:

Grid Resilience, Machine Learning, Smart Grids, Time-domain Analysis, Dynamic Security Assessment

1. Introduction

In the wake of new vulnerabilities such as those arising from severe weather events and cyber-attacks, current electric grids can no longer be allowed to operate as they did in the past. It is becoming increasingly difficult to analyze different combinations of contingencies under changing scenarios. Grid resilience and improved situational awareness will form the basis of future electric grids in order to tackle these new challenges. The most cost effective way to meet such stringent requirements is through intelligent operation of the grid by employing data driven models that are both informational and analytical in nature. The key attribute involved here is the ability to assess the current state of the power system in real-time in terms of its security. Power system security is defined as its ability to survive imminent disturbances (contingencies) without interruption of customer service. Historically, it has been recognized that for a power system to be secure, it must be stable against all types of disturbances [1] [2] . Hence, stability analysis is an important component that can facilitate the assessment of power system security and thus, its resiliency.

Security in terms of operational requirements implies that following a sudden disturbance, power system would be secure if and only if: 1) it could survive the transient swings and reach an acceptable steady state condition, and 2) there are no limit violations in the new steady state condition. The first requirement can be met by carrying out time-domain simulations in order to investigate the instability phenomena such as loss of synchronism or voltage collapse in the post-contingency transient phase. The second requirement is met by using power- flow based methods in order to assess the new steady state condition for voltage and current limit violations.

Time-domain simulations (TDS) are computationally involved and too complex to be performed in real-time. Therefore, for many years in the past, the electric utility industry’s framework for real-time security assessment mainly consisted of solution methods that would meet only the second requirement stated earlier. Such a type of real-time security analysis is prevalent even today and is commonly referred to as “Static Security Assessment (SSA)”. On the other hand, a “Dynamic Security Assessment (DSA)” procedure would strive to meet both the requirements (as stated earlier) in real-time in order to assess power system security.

Different forms of DSA practices have existed in North America since the late 1980s [3] . Modern DSA implementations are able to complete a computation cycle within 5 - 20 minutes after a real-time snapshot (base case) of the system is available [4] . Real-time snapshots are provided by existing SCADA-based state estimators every few seconds or minutes depending on the size of the system [5] -[9] . Thus, these modern DSA implementations can be termed as “near real-time” and not “real-time”. However, the latest PMU-based data collection technology can provide much better snapshots wherein the measurements are transmitted to the main control center at rates as fast as 60 samples/second [10] . Thus, DSA implementations of the future will be required to handle large amounts of data and complete the computation cycles much faster in order to assess the system security in true “real-time”. Mathematically, such an instantaneous assessment would be possible only if grid resilience against any contingency can be expressed as a function of the state estimator output. In other words, input to the data-driven models must consist of only steady-state (static) quantities namely bus voltages and bus angles derived from power-flow based methods.

Machine learning (ML) techniques have the ability to assimilate and reason with knowledge the way human brain does. Such techniques are primarily driven by data that could be in the form of various power system parameters such as [11] -[13] : voltage, current, power, frequency, power angles etc. ML techniques can capture the nonlinear dynamics of power systems by extracting useful information from such large amounts of data. DSA tools employing such ML techniques will have the ability to determine stability limits in real-time. Such sophisticated tools will be able to analyze the current and future dynamics of power systems without carrying out extensive time-domain simulations. Additionally, these tools would also benefit the system operators by providing them with real-time information on trends in system security, thereby facilitating faster decision-making during crucial times. Also, as the entry of renewable energy systems further increases grid complexity, it is possible to extend the proposed work in order to accommodate online training, thereby resulting in a smart tool that can very effectively assess the system security in real-time.

This paper presents a framework that would enable implementation of such powerful machine learning techniques for real-time assessment of grid resilience. A standard IEEE 14-bus system is used in this paper for simulation purposes [14] . Firstly, a set of multiple steady-state operating points is generated by performing a SSA on the base case. Secondly, a TDS is performed on each operating point to assess the grid resilience against a specific contingency, thus generating a dataset for this work. The paper highlights the importance of selecting a few cases as landmark points in the operational space under consideration. Further, it presents a procedure to select the best landmark points in order to improve the prediction accuracy on the original dataset, thereby enhancing the ability to assess grid resilience instantaneously.

2. Static Security Assessment (SSA)

Static security assessment (SSA) provides a mathematical framework to compute stability limits for individual buses and lines based on power flow based methods. This involves checking for steady state voltage violations at every bus in the system. Power-Voltage (PV) curves are plotted for each bus by systematically loading the base case of the power system under consideration. This is achieved by means of an algorithm called as “Continuation Power Flow (CPF)” [15] .

CPF is a “case worsening” procedure where the power system is loaded in steps as follows:

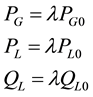(1)

where P_G0, P_L0, Q_L0 are the base case generator and load powers (in per-unit) and λ is the loading parameter (in per-unit). CPF facilitates plotting of voltage curves as a function of loading parameter λ, for each bus.

As stated earlier, such a framework can be used to generate a dataset consisting of multiple steady-state operating points. For an n-bus system, every such operating point can be represented by a feature vector x of dimension 2n consisting of n bus voltages and n bus angles as features. A set S containing such objects is given by,

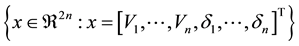(2)

where V_i’s are bus voltages (in per unit) and δ_i’s are bus angles (in degrees).

SSA is performed on the standard IEEE 14-bus system for the following voltage stability criteria at each bus: V_max = 1.2 pu and V_min = 0.8 pu. Generators are represented by machine models along with automatic voltage regulators and turbine governors. A CPF routine is performed for each line outage of this power system. Thus, a maximum loading parameter λ_maxi is calculated for each line outage i, taking voltage stability criteria into account. The set represented by Equation (2) is generated only for values of λ given by,

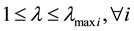(3)

It has to be noted that these λ_maxi values account for only steady-state voltage violations and hence, do not provide any information about dynamic system security. In order to account for dynamic stability, time-domain simulations are performed for each operating point, as described in the next section. All routines are carried out using the PSAT toolbox for Matlab [16] . Figure 1 shows V-λ curves for a particular line outage.

3. Dynamic Security Assessment (DSA)

The goal of a DSA is to classify different cases based on their dynamic security severity. Dynamic security depends on the time responses of various system variables for the contingency under consideration. As mentioned earlier, it is not possible to perform computationally intensive time-domain simulations in real-time. Nonetheless, machine learning techniques have the ability to extract information from offline time-domain simulations. Subsequently, such useful information can be used to predict dynamic system security for new configurations in order to avoid lengthy time-domain simulations. To implement such an application, detailed time-domain simulations are required to be conducted for different operating points. Thus, a database, on which ML techniques can operate, needs to be generated in offline mode.

The database is generated in the form of a feature matrix X and an output vector y. Each row of the feature matrix X represents a steady state operating point in the form of object 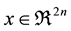from set S as defined in equation (2). Matrix X contains total number of ’m’ such objects and hence, its size is (m × 2n). A time-domain simulation for a specific contingency is performed on each of these m objects. These simulations are tagged as “stable” or “unstable” depending on the time responses of system variables. Output vector y is a binary column vector with m rows wherein each row represents whether the corresponding TDS is stable(1) or unstable(0). For the IEEE 14-bus test system considered in this paper, a load disturbance of 0.2 per-unit (increase) is applied to every steady state operating point generated in the previous section. Stability is decided based on the average values of voltage violations over the entire simulation period (V_max = 1.2 pu and V_min = 0.8 pu). Figure 2(a) and Figure 2(b) show voltage dynamics at all buses for a stable and unstable case respectively.

Essentially, DSA is a mapping between each object x and its resiliency against the contingency under consideration, expressed by function f such that,

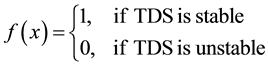(4)

The next section describes the application of machine learning techniques in order to arrive at this unknown function f.

4. Application of Machine Learning Techniques

Machine learning techniques can be applied to the database as generated in the previous section in the form of feature matrix X (size m × 2n) and output vector y (size m × 1). Each row i of matrix X is in the form of object 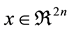from set S as defined in Equation (2) and is referred to as the i^th training example: x⁽ⁱ⁾. Similarly, the i^th

row from vector y represents the output of the i^th training example and is represented by a bit y⁽ⁱ⁾ (either 0 or 1). Therefore, we have,

x⁽ⁱ⁾ = i^th training example

y⁽ⁱ⁾ = output (stability) of the i^th training example

For “2n” features and “m” training examples, matrix X and vector y are given as follows,

(5)

Next, a prediction/hypothesis function h in terms of parameter vector q (column vector) of size 2n is proposed as follows,

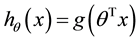(6)

where x is any training example vector and g depends on the machine learning algorithm being employed.

The cost function J for machine learning algorithms is generally of the form [17] ,

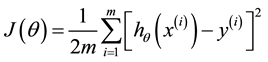(7)

The above cost function is the mean of the sum of squared errors in predicting the outputs of m training examples. Such a cost function can be minimized by using analytical method or batch gradient descent method. The optimal parameter vector q thus derived can be used for predicting the stability of future cases in real-time.

The problem presented in this paper is to classify a TDS as stable (1) or unstable (0). For such classification problems, logistic regression can be used, in which case functions g and J are given as follows [18] ,

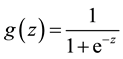(8)

and

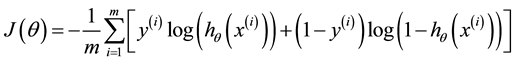(9)

The function g(z) given in equation (8) is a sigmoid function and its value lies between 0 and 1. For classification purposes, TDS cases for which g(z) is greater than 0.5 can be considered as stable and the rest as unstable. At this point, it should be noted that function h given in equation (6) approximates the unknown function f of the previous section, when the parameter q is optimal. The approximated function f_apprx can be given by,

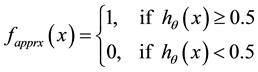(10)

In order to test the algorithm, the 14-bus dataset represented by matrix X and vector y (as generated in the previous section) can be divided into a training set (75%) and a test set (25%), which is a normal practice in ML domain. We may also delete the constant feature columns from X such as those containing PV bus voltages and reference angles, since such constant feature values do not add any valuable information. Therefore, an original matrix X with 22 columns (features) is used in this paper. Figure 3(a) and Figure 3(b) show the learning curves for the training and test sets respectively. Learning curves are plotted by varying the number of examples m in the training set. As highlighted in these figures, the average prediction errors on the training and test sets are calculated as 1.245% and 2.599% respectively. For m objects, prediction error is the percentage of examples that are classified incorrectly by the function f_apprx given in Equation (10) and it is calculated as follows,

(11)

The next section of this paper introduces the concept of “landmark points” and “linear kernel”. Further, this paper presents a strategy to select best landmark points in order to improve the prediction accuracy.

5. Landmark Points and Linear Kernel

The concept of selecting landmark points gains importance from the fact that a few training examples may contain the most relevant information about the inherent dynamics present in the dataset [19] . This section investigates the possibility of selecting such landmark points within the operational space under consideration in order to improve prediction accuracy without compromising computational efficiency. Essentially, these landmark points are 2n-dimensional objects belonging to the same set S given by Equation (2).

In order to demonstrate the effectiveness of this concept, L number of landmark points are drawn at random from the rows of matrix X and then, every (training example, landmark) pair is compared using a linear kernel [20] . A linear kernel measures the similarity between training example x⁽ⁱ⁾ and landmark l^(j)using the dot product and is given by,

(12)

Similarity is calculated between all training examples i: 1 < i < m and landmark points j: 1 < j < L. The original feature matrix X (size m × 2n) gets transformed into a new matrix (size m × L) which can be now used for training and testing purposes. Computational efficiency is maintained by enforcing the following constraint,

(13)

As shown in Figure 4(a) and Figure 4(b), prediction errors on the training and test sets decrease as the number of landmark points increase. However, it should be noted that such a random selection of landmark points does not guarantee better performance when compared with the average training and test set errors calculated in the previous section.

6. Strategy to Select Best Landmark Points

Choosing the most appropriate set of landmark points for a given dataset is not an easy task. In this section, the k-means algorithm is used to derive better landmark points as compared to the random ones selected in the previous section [21] . Using k-means algorithm, centroids can be calculated for any feature matrix X. A total number of L such centroids are generated from X for use as landmark points and then, using linear kernel a new matrix is formed like in the previous section.

In an attempt to find the best landmark points, the original matrix X is divided into 2 matrices X_stable and X_unstable consisting of only stable and unstable cases respectively. Using k-means, a total number of L centroids are generated for each of these matrices separately and again using linear kernel, two new matrices and are formed.

The strategy for selecting best landmark points can be stated as follows,

・ Select L random examples from original matrix X as landmarks and generate

・ Select L centroids from original matrix X as landmarks and generate

・ Select L centroids from X_stable as landmarks and generate

・ Select L centroids from X_unstable as landmarks and generate X’_unstable

・ Plot learning curves using, , ,

・ Compare the training and test set errors and select the best L landmarks

Figure 5(a) and Figure 5(b) show the learning curves for each of the above matrices with L = 22 landmarks for the IEEE 14 bus dataset generated earlier. From these figures we can conclude that centroids selected from the unstable cases are the best landmark points for this dataset. Moreover, it has to be noted that computational efficiency is not compromised since the total number of landmarks used here (L = 22) is not greater than the total number of columns in the original matrix X (=22). Figure 6(a) and Figure 6(b) again compare the learning with increasing number of land marks for the case of random landmarks against landmarks selected as centroids from only unstable cases. Figure 7(a) and Figure 7(b) plot the learning curves for the original matrix X (without any landmarks) and (best landmarks). These plots confirm that when best landmarks are employed, prediction accuracy improves on both, the training set and the test set.

7. Concluding Remarks

The ability to assess the current state of the power system instantaneously is the key attribute needed for enhanced grid resilience. Electric power entities carry out large number of offline studies on power system models of different sizes, thus generating tons of data. Machine learning techniques can be employed to use such huge databases in order to learn the inherent non-linear relationships that exist among different power system parameters. Such useful information can be later used online for real-time security analysis.

This paper presents a framework to apply machine learning techniques for real-time assessment of the grid resilience against any contingency with respect to its static and dynamic stability using offline databases. Further, this paper demonstrates a strategy to select best landmark points in order to improve prediction accuracy without compromising computational efficiency. Moreover, ML algorithms are easily scalable and hence, the proposed approach can be extended for analyzing grid resilience against multiple contingencies. Metrics for grid resilience can be developed based on such multi-contingency analyses. With large-scale penetration of renewable energy

in to the current grid and emergence of microgrids, future grid applications would require real-time training in order to extract useful information on a continuous basis. Machine learning techniques can accommodate such complex requirements posed by the continually changing electric grid and hence, would definitely play an important role in realizing next-gen real-time applications.

Acknowledgements

This work was supported by the OSU Engineering Energy Laboratory and the PSO/Albrecht Naeter Professorship in the School of Electrical and Computer Engineering.

Cite this paper

NavinShenoy,R.Ramakumar, (2015) An Approach to Assess the Resiliency of Electric Power Grids. Journal of Power and Energy Engineering,03,1-13. doi: 10.4236/jpee.2015.311001

References