Journal of Power and Energy Engineering
Vol.03 No.02(2015), Article ID:54338,6 pages
10.4236/jpee.2015.32001
Control of Instable Chaotic Small Power System
Samir M. Al Shariff1*, Ahmad M. Harb2
1Electrical Engineering Department, Taibah University, Madina, Saudi Arabia
2Energy Engineering Department, German Jordanian University, Amman, Jordan
Email: *samshariff@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2015; accepted 25 February 2015; published 28 February 2015
ABSTRACT
In this paper, we aim to control an instable chaotic oscillation in power system that is considered to be small system by using a linear state feedback controller. First we will analyze the stability of the mentioned power system by means of modern nonlinear theory (Bifurcation and Chaos). Our model is based on a three bus power system that consists of multi generators containing both dynamic and static loads. They are considered to be in the form of an induction motor in parallel with a capacitor, as well as a combination of constant power along with load impedance, PQ. We consider the load reactive power as the control parameter. At this stage, after changing the control parameter, the study showed that the system is experiencing a subcritical Hopf bifurcation point. This leads to a chaos within the system period doubling path. We then discuss the system controllability and present that the all chaotic oscillations fade away through the linear controller that we impose on the system.
Keywords:
Bifurcation, Instable Chaotic Oscillation, Linear Controller, Voltage Collapse, Chaotic Oscillation Fade Away, Small Power Systems

1. Introduction
In the past so many researchers have used the voltage collapse case study within a power system. Here, the power system performs as a significant part of the sequential event that is accompanied by an unstable voltage profile [1] . This voltage collapse will lead to load losses that will be yielded into a tripping on the load lines and subsequently, a total shutdown will affect the considered area. The Kingdom of Saudi Arabia, United States of America, United Kingdom, Japan, France and many other countries have had several incidents that are associated with the collapse of voltage leading into a total area shutdown. There are so many reasons that contribute to these incidents. Some of which are focused on the loads whether it is high or low on the tap changing transformers and the reactive power injected at the bus. All these will lead to a voltage level breakdown. In order to control the voltage collapse occurrence, several techniques may be applied such as Static Var Compensator (SVC), and Series Capacitor Bank (SCB).
Throughout the past most of the work that was conducted would have linked the voltage collapse to a static bifurcation done by Kwatny et al. [2] , Schlutere et al. [3] , and Thomas and Tiranunchit [4] . While, the dynamic bifurcation was linked by Abed and Varaiya [5] , Abed et al. [6] , Rajagopalan et al. [7] , Dobson et al. [8] , and Nayfeh et al. [9] .
Combining both control theories along with the applications of bifurcation theory is a challenge and great interest to many researchers in the design of controllers for nonlinear systems that exhibit bifurcations models. Both Abed and Fu [10] [11] have detailed combination of working on feedback stabilization and bifurcation control simultaneously. Abed et al. [6] and Chiang et al. [12] looked at the issue of utilizing the concept of nonlinear control in power system. Subsequently, Baillieu et al. [13] have studied nonlinear feedback system while at a chaotic motion. In addition, Chang & Chen [14] have investigated bifurcation characteristics under PID controller for nonlinear systems.
Recent studies are directed at combining control of bifurcation along with chaos in dynamical system simultaneously. Thus, the emphasis will be weighted on design techniques that will result into a prescribed nonlinear dynamic system for the controlled processes. Moreover, bifurcation control stimulates its usage by a control input modifying its bifurcation characteristics for the parameterized system. The control model will be considered for a static or a dynamic feedback and with an open loop system.
Our objective is to control, stabilize, and delay a given bifurcation. We also aim for reducing the bifurcation amplitude, getting a bifurcation solution, and finally optimizing the performance index located near the bifurcation.
In the end, we reshape the bifurcation diagram of the system [10] . Using the controlled laws derived and used in [10] , we transform an unstable subcritical bifurcation point into a point to be considered as supercritical stable bifurcationized. These control laws are called “static state feedback” and have the general form of u = u(x). These results have a wide span of applications. These applications are not limited to subsynchronous resonance in power system [15] , as well as the voltage collapse in electrical power system [16] .
2. Mathematical Model
The small power system model is known to be highly nonlinear dynamic system. It is represented by an algebraic along with a set of ordinary differential equations. In this paper, we followed the work done by Nayfeh et al. [9] considering a model that represent the load by an induction motor, a capacitor, constant power and constant impedance PQ load. The three bus power system consists of two generators feeding a load, which is represented by an induction motor in parallel with a capacitor and combined with a PQ load. One generator is considered as an infinite bus while the other generator has a constant voltage magnitude of Em. After Nayfeh et al. [9] , the following set equations governs the small power system and are written as:
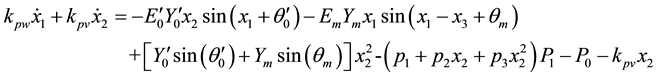 (1)
(1)
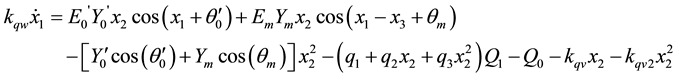 (2)
(2)
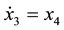 (3)
(3)
 (4)
(4)
Now, we add the linear control systems, thus the state-space equations are coupled to the previous four equations resulting into:
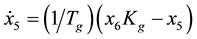 (5)
(5)
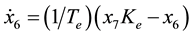 (6)
(6)
 (7)
(7)
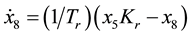 (8)
(8)
where x1 and x3 are the power angles of the machine and the load, respectively. Furthermore, x2 is the load voltage, and x4 is the radian frequency of the load, while x5, x6, x7, and x8 are the exciter, amplifier, proportional controller, and the sensor, respectively. The above eight equations provide an equilibrium solution along with a dynamic solution to our model. Table 1 shows the load and generator parameters that have been used. All the parameters are given in per unit except for the angles, which are measured in degrees.
3. Numerical Simulation
The equilibrium solutions are found by setting of the system of equations (1)-(8) to be equal to zeros. The stability of these solutions depends on the eigenvalues of the Jacobian matrix of set of equations (2)-(8) evaluated each at the equilibrium point.
Table 1. Parameters for the load and generator.
Nayfeh et al. [9] studied a small power system using theories of bifurcation theory that are shown in Figure 1. They have noticed that the small power system experiences a dynamical bifurcation (Hopf bifurcation). There are two Hopf bifurcation points H1 and H2 at the control parameters Q1 = 6.9929 and 7.2229, respectively, and a saddle-node bifurcation SN at Q1 = 7.2238. They have also found that the two Hopf bifurcation points H1 and H2 are subcritical and supercritical points respectively, as shown in the bifurcation diagram in Figure 2. They showed that the system experiences the limit cycle and then period-two, period-four, and so on till the behavior of the system became chaotic. Figure 3 shows the chaotic oscillation of the system. Hence, for values of 6.9105 ≤ Q1 ≤ 6.9449957, the system response may be constant or dynamic (limit-cycle or chaos), depending on the initial conditions. Because the chaos is very sensitive to initial condition.
In order to control and eliminate the chaotic oscillations, a linear control via proportional controller must be added to the system. This linear controller will fade away the eighth order system of equations (1)-(8). The subcritical Hopf bifurcation, H1 and hence control chaos and voltage collapse there, a nonlinear feedback controller is designed by Nayfeh et al. [9] . Their controller transforms the left Hopf bifurcation point, shown in Figure 3, from a subcritical into a supercritical one as indicated in Figure 3. They have also used a nonlinear controller that has the form of Kω3 and it is added to equation (2). They show that by increasing the value of K, we will reduce the amplitude of the limit-cycle born at H1. Furthermore, by choosing a gain K larger than a critical value of 58.56, one can suppress the period-doubling bifurcations and hence the chaos and its associated crisis bifurcation and voltage collapse as shown in Figure 3. In this paper the linear added controller, equations (6)-(8), were able to eliminate all chaotic oscillations and are shown in Figures 4-6.
Figure 1. Small power system dynamical bifurcation (Hopf bifurcation) circuit.
Figure 2. Bifurcation diagram showing two Hopf bifurcation points H1 and H2 that are subcritical and supercritical points.
Figure 3. The chaotic oscillation of the system.
Figure 4. Chaotic oscillations 1.
Figure 5. Chaotic oscillations 2.
Figure 6. Chaotic oscillations 3.
4. Conclusion
The modern nonlinear theories of bifurcation and chaos are applied to a small three bus power system. The results showed that the system, without any controller, has a dangerous subcritical Hopf bifurcation point. That means when 6.9105 ≤ Q1 ≤ 6.9449957, the system response may be constant or dynamic (limit-cycle or chaos), depending on the initial conditions. A comparison between the uncontrolled and controlled system was discussed and investigated. The study has revealed that the linear controller stabilizes the system by eliminating all chaotic oscillations. Hence, the system became completely stable over the whole range of the control parameter point Q1.
Acknowledgements
We would like to acknowledge the funding of this project (08-ENE416-5) by the Science and Technology Unit at Taibah University through the National Science, Technology, and Innovation Plan for Saudi Arabia.
References
- Kundur, P. (1994) Power System Stability and Control. Electric Power Research Institute, (McGraw-Hill, Inc.), New York.
- Kwatny, H.G., Pasrija, A.K. and Bahar, L.Y. (1986) Static Bifurcation in Electric Power Networks: Loss of Steady- State Stability and Voltage Collapse. IEEE Transactions on Circuit and Systems, 33, 981-991. http://dx.doi.org/10.1109/TCS.1986.1085856
- Schlueter, R.A., Costi, A.G., Sekerke, J.E. and Forgey, H.L. (1988) Voltage Stability and Security Assessment. EPRI Final Report El-5967 on Project RP 1999-8.
- Thomas, R.J. and Tiraunchit, A. (1987) Dynamic Voltage Instability. Proceedings of the 26th IEEE Conference on Control and Decision, Los Angeles, 9-11 December 1987, 53-58.
- Abed, E.H. and Varaiya, P.P. (1989) Nonlinear Oscillations in Power Systems. International Journal of Electrical Power & Energy Systems, 6, 37-43. http://dx.doi.org/10.1016/0142-0615(84)90034-6
- Abed, E.H., Alexander, J.C., Wang, H., Hamdan, A.H. and Lee, H.C. (1992) Dynamic Bifurcation in a Power System Model Exhibiting Voltage Collapse. Proceedings of the 1992 IEEE International Symposium on Circuit and Systems, San Diego, 10-13 May 1992, 2509-2512.
- Rajagopalan, C., Sauer, P.W. and Pai, M.A. (1989) Analysis of Voltage Control System Exhibiting Hopf Bifurcation. Proceedings of 28th IEEE Conference on Decision and Control, Tampa, 13-15 December 1989, 332-335.
- Dobson, I., Chiang, H.-D., Thorp, J.S. and Fekih-Ahmed, L. (1988) A Model of Voltage Collapse in Electric Power Systems. Proceedings of the 27th IEEE Conference on Decision and Control, Austin, 7-9 December 1988, 2104-2109.
- Nayfeh, A.H., Harb, A.M. and Chin, C. (1996) Bifurcation in a Power System Model. International Journal of Bifurcation and Chaos, 6, 497-512.
- Abed, E.H. and Fu, J.H. (1986) Local Feedback Stabilization and Bifurcation Control, I. Hopf Bifurcation. System and Control Letters, 7, 11-17. http://dx.doi.org/10.1016/0167-6911(86)90095-2
- Abed, E.H. and Fu, J.H. (1987) Local Feedback Stabilization and Bifurcation Control, II. Stationary Bifurcation. System and Control Letters, 8, 467-473. http://dx.doi.org/10.1016/0167-6911(87)90089-2
- Chiang, H.-D., Dobson, I., Thomas, R.J., Thorp, J.S. and Fekih-Ahmed, L. (1990) On Voltage Collapse in Electric Power Systems. IEEE Transactions on Power Systems, 5, 601-611. http://dx.doi.org/10.1109/59.54571
- Baillieul, J., Brockett, R. and Washburn, R.B. (1980) Chaotic Motion in Nonlinear Feedback Systems. IEEE Transactions on Circuits and Systems, 27, 990-997. http://dx.doi.org/10.1109/TCS.1980.1084739
- Chang, H.-C. and Chen, L.-H. (1984) Bifurcation Characteristics of Nonlinear Systems under Conventional PID Control. Chemical Engineering Science, 39, 1127-1142. http://dx.doi.org/10.1016/0009-2509(84)85075-7
- Harb, A.M., Nayfeh, A.H., Chin, C. and Mili, L. (1999) On the Effects of Machine Saturation on Subsynchronous Oscillations in Power Systems. Electric Machines and Power Systems Journal, 28, 1019-1035.
- Wang, H.O. and Abed, E.H. (1993) Control of Nonlinear Phenomena at the Inception of Voltage Collapse. Proceedings of the 1993 American Control Conference, San Francisco, 2-4 June 1993, 2071-2075.
NOTES
*Corresponding author.










