Journal of Power and Energy Engineering
Vol.03 No.01(2015), Article ID:53017,9 pages
10.4236/jpee.2015.31001
Numerical Investigation of Wind Flow around a Cylindrical Trough Solar Collector
Seyyed Mohammad Nima Shojaee1, Mohammad Adel Moradian2, Mashhood Mashhoodi3*
1Faculty of Mechanical and Aerospace Engineering, Science and Research Branch, Islamic Azad
University, Tehran, Iran
2School of Mechanical and Manufacturing Engineering, University of New South Wales, Sydney, Australia
3Young Researchers and Elites Club, Science and Research Branch, Islamic Azad University, Tehran, Iran
Email: m.moradian@unsw.edu.au, *mashhoodi@aut.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 November 2014; revised 14 December 2014; accepted 27 December 2014
ABSTRACT
The goal of this study is to model the effects of wind on Cylindrical Trough Collectors (CTCs). Two major areas are discussed in this paper: 1) heat losses due to wind flow over receiver pipe and 2) average forces applied on the collector’s body. To accomplish these goals a 2D modeling of CTC was carried out using commercial codes with various wind velocities and collector orientations. Ambient temperature was assumed to be constant at 300 K and for specific geometries different meshing methods and boundary conditions were used in various runs. Validation was done by comparing the simulation results for a horizontal collector with empirical data. It was observed that maximum force of 509.1 Newton per Meter occurs at +60 degrees. Nusselt number is almost the constant for positive angles while at negative angles it varies considerably with the collector’s orientation.
Keywords:
Component, Flow Analysis, Wind Forces, Solar Collectors, Cylindrical Trough Collector, Computational, Solar Energy

1. Introduction
Fossil fuels as a major source of energy have many advantageous such as low price, high availability and can produce a significant amount of energy per unit of weight. However, the environmental consequences of extensive use of fossil fuels, especially coal, are manifesting themselves through global warming and similar phenomena. According to [1] global greenhouse gas emissions from human sources have risen to 49 GtCO2-eq/yr which has caused an increase in atmospheric carbon concentration from a pre-anthropogenic level of 280 ppm to 379 ppm in 2005. These global changes are pushing industries and politicians to find sustainable solutions to humanity’s ever growing energy demands.
Solar energy as an alternative is a clean, renewable and inexhaustible source of energy. All other forms of energy that we use are solar in origin. Oil, coal, natural gas and woods were originally produced by photosyn- thetic processes, followed by complex chemical reactions in which decaying vegetation was subjected to very high temperatures and pressures over a long period of time [2] . The idea of using sun’s energy is not a new one as it can be predated to the ancient Greek civilization [3] . More recent and industrial use of solar energy can be seen in 18th century when concentrating solar were used as “solar furnaces” to melt iron, coper and other metals [4] . During the last 50 years many variations were designed and constructed using focusing collectors as a means of heating the transfer or working fluid which powered mechanical equipment [5] .
The two primary types of solar collectors that are using are distributed receivers and central receivers. This study is concerned with a specific type of distributed receivers called as trough collectors. Trough collectors are line-focus tracking reflectors that concentrate sunlight onto receiver tubes along their focal lines. Other types of distributed receivers include parabolic dishes, Fresnel lenses, and special bowls [6] . Industries choose the type of collector based on the temperature range that a certain type of collector can reach. This range is shown in Table 1 [3] .
Sadly after 70’s, due to poor policies, progress in solar thermal power slowed down. However, the last five years have seen a resurgence of interest in this area [7] .
According to Reference [8] up to 27% of industries require thermal energy up to 200◦C, this makes cylindrical trough collectors a feasible option for most of such industries.
CTC’s are made by bending a sheet of a reflective material into a cylindrical shape, then a tube which is covered with another glass tube (to reduce heat loss) is placed at the focal line. This called “receiver tube”. When the collector is facing the sun, some rays that hit the reflector surface are reflected on the receiver tube. It is these reflected rays that heat up the working fluid which is flowing in the receiver tube. For efficient performance, CTC’s have to face the sun at tall time hence they are usually equipped with a single axis tracking system. This means that at different times of day reflector surface will have different orientation. Reflectors orientation can have a significant impact on structure and thermal efficiency of the collector.
Several studies have been carried out on solar collectors such as, wind load on residential and large scale solar collector models [9] which were used as solar water heaters, heat transfer coefficient on flat plate solar collectors and solar cookers [10] , thermal modeling of an unglazed flat solar panel collector [11] , determining of heat transfer coefficient for forced convection on rectangular solar collectors [12] , heat transfer characteristics in the receiver tube of a parabolic trough collector [13] , wind flow around a PTC installed in Shiraz [14] and Nusselt number range for the mentioned PTC in Shiraz [15] . On the very track this research has two main purposes: 1) To determine the forces acting on the cylindrical trough collector due to wind and their relationship with reflector surface’s orientation; 2) To ascertain the amount of receiver pipe’s heat loss.
Table 1. Temperature range for different collectors.
2. Materials and Methods
Geometry of this study consists of a CTC with variable collector angles. Collector is a 60 degree section of a 140 cm diameter cylinder as illustrated in Figure 1. Receiver tube with diameter of 4.2 cm which is placed at reflector’s focal line (70 cm from the reflector surface) as can be seen in Figure 2. Seven control volumes and meshes were generated to solve the problem at all angles of the study (0, ±30, ±45, and ±60).
Grid structure is of critical importance in any CFD problem due to its contribution to accuracy and convergence efficiency. For this reason a structured c-h type grid is applied in the domain by Gambit. Boundary’s which were defined in the control volume are shown in Figure 2. The boundary conditions are as follow: wind enters at the velocity inlet with 4 different speeds and a constant temperature of 300 K. Ground, reflector surface and receiver pipe are all solid walls. Receiver pipe’s surface is assumed to have a constant temperature of 350 K (based on [15] ). Both pressure outlets are atmospheric pressures. Ground and reflector temperatures are assumed to be the same as the ambient temperature (300 K). Due to wind speed and dominance of forced convection, natural convection was neglected. Air was deemed to be incompressible due to assumed constant density.
As it can be seen from Figure 3(a) and Figure 3(b), a c-type grid is applied to the regions that are close to the wall to efficiently model the pipe wall curves and H-type grid which excels at predicting the vortices, is used downstream of the pipes. Figure 3(a) and Figure 3(b) show the geometry and mesh for 0 and 30 degrees that were made by Gambit.
Figure 1. Schematic of the system. Collector at 30 degrees and the receiver tube.
Figure 2. Boundary conditions.


Figure 3. Simulated software in the system. (a) Geometry and mesh at 0 degree; (b) Geometry and mesh at 30 degrees; (c) Flow over receiver tube at 0 degree; (d) Wind flow at 0 degree.
Simple pressure-velocity coupling, energy equation and RNG k-ɛ model (derived by renormalization group theory) was used in Fluent to solve the problem. This model is derived from the instantaneous Navier-Stokes equation using a mathematical technique known as Re-Normalization Group method hence the abbreviation RNG. RNG model which is similar in form to other k-ɛ models was proposed by [16] and has features that make it more accurate and reliable for wider class of flows than standard k-ɛ models. The RNG turbulence model is more responsive to the effects of rapid strain and streamlines curvature, flow separation, reattachment and re- circulation than the standard k-ɛ model and it has been used widely for wind flow studies [15] .
In order to validate the computational analysis, two different methods were used, one was to verify Nusselt number and the other was to verify drag coefficient.
At 0 degree, the flow over the receiver pipe is perpendicular to receiver pipe (as can be seen in Figure 3(c) and Figure 3(d)) therefore, to verify the results for heat transfer, Nusselt number from numerical analysis was compared to the Nusselt number from the Equation (1) which is given in (Çengel, 2002) [17] .
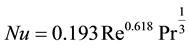 (1)
(1)
Figure 4 shows the Nusselt number from Equation (1) versus the computational method.
In order to verify drag coefficient, a 180 degree sector of an empty cylinder (10 cm diameter) was modeled in Gambit and analyzed in Fluent with similar methods. Afterwards, pressures on both sides of the half-cylinder were plotted against the vertical axis (y) and through curve fitting, the pressure was estimated as a function of height. By integrating the pressure function between y = −0.05 and y = 0.05 and using Equation (2), the drag coefficient was calculated.
Comparison between the results from the computational analysis and drag coefficient given in [18] shows an error of about 5% which is in part due errors in curve fitting and thus acceptable.
 (2)
(2)
3. Results and Discussion
Steady state flow in the control volume was analyzed using computational methods at 0, ±30, ±45 and ±60 collector angles and various wind velocities (2.5 m/s, 5 m/s, 10 m/s and 15 m/s) as inlet boundary condition. Con-
Figure 4. Nusslet number from Equation (1) versus Nusslet number from computational.
vergence of the numerical solution was obtained when the residual of each of the governing equations was less than 1e−5. Table 2 shows the mean forces acting on the collector’s body. Based on these results, Equation (3) was derived by numerical methods to calculate the forces acting on the collector for different angles and speeds.
Figure 5 shows the velocity contours for all seven collector angles at the inlet Velocity of 10 m/s.
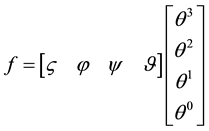 (3)
(3)
where θ is the collector angle in degrees. Values of ς, φ, ψ and ϑ which are required for calculating the net force are given in Equation (4).
 (4)
(4)
where V is wind velocity. Equation (5) calculates the values of ς, φ, ψ and ϑ that are required for calculating the drag force:
 (5)
(5)
In order to achieve acceptable precision, a higher degree polynomial equation (Equation (6)) is derived for calculating the lift force.
 (6)
(6)
In Equation (6), fl is the lift force and θ is the collector angle. All the other variables are defined in Equation (7) to Equation (13).



Figure 5. Velocity contour for different collector angles. (a) Velocity contour for 30 degrees; (b) Velocity contour for −30 degrees; (c) Velocity contour for 45 degrees; (d) Velocity contour for −45 degrees; (e) Velocity contour for 60 degrees; (f) Velocity contour for −60 degrees.


Table 2. Forces for different collector angles.





Figure 6 shows the forces acting on the collector versus the collector angle at different wind speeds. It can be concluded from Figure 6 that at −18 degrees, the net lift force is zero. This is due to the fact that at this angle the sum of vertical forces caused by change in momentum and pressure gradient are at opposing directions and


Figure 6. Wind forces acting on the collector. (a) Net forces acting on the collector; (b) Drag forces acting on the collector; (c) Lift forces acting on the collector.
have the same value. Another interesting fact about the lift force is that it reaches its peak at about +45 degrees. At 0 degree, as is obvious, the drag force is minimal for all speeds. Based on Table 2 the forces acting on the collector are smaller when the collector angle in negative. This is because of the semi-aerodynamic shape of the collector in negative angles. This semi-aerodynamic shape reduces the pressure gradient and therefore reduces the drag force. In case of positive angles (especially above 45 degrees), unlike negative angles, larger pressure gradient causes an increase in drag force. Figure 7 shows the pressure contours for ±30 degrees orientations at wind velocity of 10 m/s.
As can be seen in Figure 5, the alteration of the collector angle affects the flow over the receiver pipe which directly affects the forced convention and in turn, changes the Nusselt number. Figure 8 shows the Nusselt number versus wind speed at different collector angles.
Based on Figure 8, it can be interpreted that the Nusselt number variation versus wind speed follows a similar pattern regardless of collector orientation but at the same time, changes in collector angle can drastically change Nusselt number at a certain wind speed. As an example, while at −60 and −30 both curves have similar slope however, at a certain wind velocity of 4 m/s Nusselt number is almost three times more for −30 orientation com- pared to −60 orientation.
4. Conclusions
It is desirable to reduce the Nusselt number and consequently the heat losses caused by wind in solar collectors. At positive angles, the flow over the receiver pipe is almost cross flow therefore, regardless of collector angle the average Nusselt number almost remains constant for a fixed speed. But as for the negative angles, while collector is at smaller than 15 degrees angles, the flow over the receiver pipe is cross flow. At medium angles (15 to 45 degrees) the flow crosses the receiver pipe with a higher velocity which increases the heat loss. For large angles (larger than 45 degrees) the collector covers the receiver pipe therefore the Nusselt number is reduced.


Figure 7. Pressure contour at different reflector angles. (a) Pressure contour at −30 degrees; (b) Pressure contour at +30 degrees.
Figure 8. Nusselt number vs wind speed for different angles.
Based on the results of this study, it is suggested that industries should consider structural forces and heat losses caused by wind before considering the use of CTC technology.
References
- Mostofi, M., Nosrat, A.H. and Pearce, J.M. (2011) Institutional Scale Operational Symbiosis of Photovoltaic and Cogeneration Systems. International Journal of Environmental Science and Technology, 8, 31-44. http://dx.doi.org/10.1007/BF03326193
- Goswami, D.Y., Kreith, F. and Kreider, J.F. (1999) Principles of Solar Engineering. 2nd Edition, Taylors & Francis Co., Philadelphia.
- Delyannis, A. (1967) Solar Stills Provide Island Inhabitants with Water. Sun at Work, 10, 6-8.
- Meinel, A.B. and Meinel, M.P. (1976) Applied Solar Energy. An Introduction. Addison-Wesley Pub. Co., Michigan.
- Kalogirou, S. (2004) Solar Thermal Collectors and Applications. Progress in Energy and Combustion Science, 30, 231- 295. http://dx.doi.org/10.1016/j.pecs.2004.02.001
- Stine, W.B. (1987) Power from the Sun: Principles of High Temperature Solar Thermal Technology. Solar Energy Research Institute, Colorado.
- Mekhilef, S., Saidur, R. and Safari, A. (2011) A Review on Solar Energy Use in Industries. Renewable and Sustainable Energy Reviews, 15, 1777-1790. http://dx.doi.org/10.1016/j.rser.2010.12.018
- Kalogirou, S. (2009) Solar Energy Engineering: Processes and Systems. Elsevier Inc., London.
- Chung, K.M., Chang, K.C. and Chou, C.C. (2011) Wind Loads on Residential and Large-Scale Solar Collector Models. Journal of Wind Engineering and Industrial Aerodynamics, 99, 59-64. http://dx.doi.org/10.1016/j.jweia.2010.10.008
- Kumar, S. and Mullick, S.C. (2010) Wind Heat Transfer Coefficient in Solar Collectors in Outdoor Conditions. Solar Energy, 84, 956-963. http://dx.doi.org/10.1016/j.solener.2010.03.003
- Stojanovic, B., Hallberg, D. and Akander, J. (2010) A Steady State Thermal Duct Model Derived by Fin-Theory Approach and Applied on an Unglazed Solar Collector. Solar Energy, 84, 1838-1851. http://dx.doi.org/10.1016/j.solener.2010.06.016
- Turgut, O. and Onur, N. (2009) Three Dimensional Numerical and Experimental Study of Forced Convection Heat Trans- fer on Solar Collector Surface. International Communications in Heat and Mass Transfer, 36, 274-279. http://dx.doi.org/10.1016/j.icheatmasstransfer.2008.10.017
- Cheng, Z.D., He, Y.L., Xiao, J., Tao, Y.B. and Xu, R.J. (2010) Three-Dimensional Numerical Study of Heat Transfer Characteristics in the Receiver Tube of Parabolic Trough Solar Collector. International Communications in Heat and Mass Transfer, 37, 782-787. http://dx.doi.org/10.1016/j.icheatmasstransfer.2010.05.002
- Naeeni, N. and Yaghoubi, M. (2006) Analysis of Wind Flow around a Parabolic Collector (1) Fluid Flow. Renewable Energy, 32, 1898-1916. http://dx.doi.org/10.1016/j.renene.2006.10.004
- Naeeni, N. and Yaghoubi, M. (2006) Analysis of Wind Flow around a Parabolic Collector (2) Heat Transfer from Receiver Tube. Renewable Energy, 32, 1259-1272. http://dx.doi.org/10.1016/j.renene.2006.06.005
- Yakhot, V. and Orszag, S.A. (1986) Renormalized Group Analysis of Turbulence: I. Basic Theory. Journal of Scientific Computing, 1, 3-51. http://dx.doi.org/10.1007/BF01061452
- Çengel, Y.A. (2002) Heat Transfer: A Practical Approach. 2nd Edition, McGraw-Hill, New York.
- Scott, J. (2005) Drag of Cylinders & Cones. http://www.aerospaceweb.org/question/aerodynamics/q0231.shtml
NOTES
*Corresponding author.













