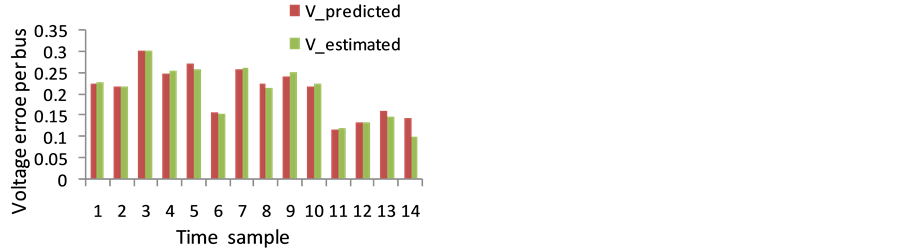Journal of Power and Energy Engineering
Vol.02 No.03(2014), Article ID:44281,10 pages
10.4236/jpee.2014.23001
Dynamic State Forecasting in Electric Power Networks
Sideig A. Dowi, Amar Ibrahim Hamza
School of Electrical and Electronics Engineering, North China Electric Power University, Beijing, China
Email: sideigdowi@yahoo.com, amarhamaza2010@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 February 2014; revised 3 March 2014; accepted 10 March 2014
ABSTRACT
The real time monitoring and control have become very important in electric power system in order to achieve a high reliability in the system. So, improvement in Energy Management System (EMS) leads to improvement in the monitoring and control functions in the control center. In this paper, DSE is proposed based on Weighted Least Squares (WLS) estimator and Holt’s exponential smoothing to state predicting and Extended Kalman Filter to state filtering. The results viewing the dynamic state the estimator performance under normal and abnormal operating conditions.
Keywords:
Dynamic State Estimation; Extended Kalman Filter; State Estimation; Electric Power Flow

1. Introduction
Recently, the power system has begun to grow very largely and more complex, so real time monitoring and control become very important in order to fulfill a reliable operation. Energy Management System (EMS) is responsible for this mission, and it forms the basis for efficient operating and control. State Estimation (SE) forms the spine of the EMS by providing the information of the real time state of the system which can be used in other EMS functions. Hence, an accurate and efficient state estimation is necessary for a reliable and efficient operation of the power system [1] [2] .
The state estimator computes the voltage magnitudes and voltage angles at the buses of the power system. We know that, power system is not a static system, but it changes very slowly with time and continuously. That means, when the load on the buses changes, the generations also have to change to overcome these changes in load. This in turn causes the change in power flows and injections at the buses, also leads to change in voltage angular at the buses and perhaps change in voltage magnitude at some buses depending on the size of this change; therefore, change the nature of the power system from static state to dynamic state nature. These dynamic behaviors of the power system are difficult to overcome by the conventional Static State Estimation (SSE). This led to the development of a new algorithm called Dynamic State Estimation (DSE) [1] -[5]. The DSE technique possesses a mathematical model for the time variation of the power system. The DSE uses this mathematical model depending on the previous state of the system at time (t), to predict the state vectors at the next state of the system (one step ahead) at time (t + 1). This capability of predicting the state one step ahead is a very important advantage in the control center, because the state forecasting gives a longer decision time to the system operator, and because the security assessment, economic dispatching and the other functions can be performed in advance. So, Dynamic State Estimation has the ability to represent an important role in the modern-day control center [1] .
In this paper, we will not only describe the dynamic model for the time behavior of the system state, but will show more details about the DSE, mainly the state predicting and state filtering. When the state variables are estimated at time k by state estimation technique, we will use these state variables to forecast the state vectors at time k + 1 using linear exponential smoothing. The state vectors are filtered based on Extended Kalman Filter and weighted least squares method. The proposal is tested using IEEE 14 bus test system. The test includes normal and abnormal operations.
2. Mathematical Models
The measurement vector consists of active power and reactive power flows and injection’s power as well as some voltage magnitudes, is denoted by an m-dimensional vector z. The power equation s is expressed by [6] [7] .
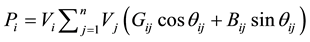 (1)
(1)
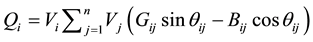 (2)
(2)
 (3)
(3)
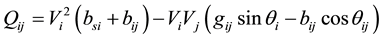 (4)
(4)
The measurement and state variable 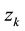 and
and 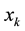 at time instant k are given by equation
at time instant k are given by equation
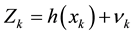 (5)
(5)
where  is measurement vector m-dimensional
is measurement vector m-dimensional ,
, 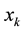 is state variables dimensioned
is state variables dimensioned ,
, 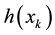 is nonlinear function relating measurement to the state vector .dimensioned
is nonlinear function relating measurement to the state vector .dimensioned  and
and 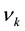 is the measurements error with zero mean and standard deviation of R.
is the measurements error with zero mean and standard deviation of R.
where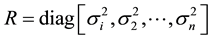 , σ is the standard deviation of error.
, σ is the standard deviation of error.
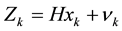 (6)
(6)
where 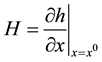
The general model for DSE is given by.

where xk and xk+1 are the state vector at instants k and k+1 respectively, Fk is nonzero diagonal matrix dimensioned (n ´ n), a function represent the state transition between two instant of time, Gk is nonzero vector associated with trend behavior of the state trajectory dimensional (n ´ 1) and wk is white Gaussian noise with zero mean and covariance matrix Q [1] -[4].
2.1. Parameters Identification
The parameters Fk and Gk are identified using Holt’s two-parameter linear exponential smoothing method [1] , [8] -[10]. This method is very simple, used when the data shows a trend. In this method, two components must be updated each period of time, level and trend.
・ The level is a smoothed estimate of the value of the data at the end of each period represented by ak. as shown in Equation (8).
・ The trend is a smoothed estimate of average growth at the end of each period. represented by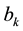
The specific model for simple exponential smoothing is written as:
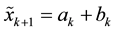
where 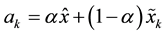
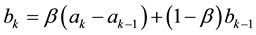

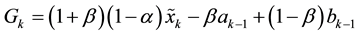
α and β represent the smoothing parameters [2] , [8] -[10].
2.2. State Predicting or State Forecasting
Let 
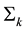
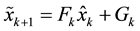
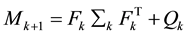
where 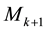
2.3. State Filtering
The forecasted state would use to forecast new measurements Zk+1 at the time k + 1 based on the data at instant k; the predicted state vector at k + 1 will be filtered to obtain new estimates (filtered states) 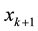
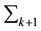

Note that, the time index (k + 1) has been omitted.
Extended Kalman Filter (EKF) used for minimizing the objective function and getting the final filtering state.
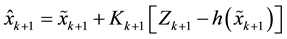
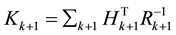
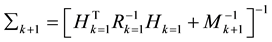
where K is called the gain matrix 
3. The Implementation
The steps of the dynamic state estimation algorithm are described above. The covariance matrix R of the measurement error is assumed to be calculated online.
where
where am & bm are the manufacture factors. st represents the real value of the measurement. sf is the maximum value of the measurement. As mentioned before, for predicting state we used Holt’s 2-exponential smoothing, the values of the smoothing parameters α and β, are fixed at 0.7 and 0.45, and for the filtering state we used Extended Kalman Filter. The elements of the covariance matrix Q of the system, is set at 10‒6. The load curve at each bus was composed of a linear trend and random fluctuation (jitter).
In this paper, the Dynamic State simulation is studied over a period of 20 time sample intervals. with increasing of constant value 5% of the load at all the buses at each period. Once the load is changed the load flow is ready to update all the real and reactive power and injection power on the lines, voltage magnitudes and angles on the system. In this paper, the actual values of the state vectors are obtained from the 14-bus IEEE standard data for the base case and load flow for rest of the time samples [11] . The test cases and their results are shown in tables and figures in the next sections.
3.1. Case Study
In this paper, we used standard IEEE 14-bus test system [11] . The measurement vector consists of 34 observations distributed as in Table 1.
The measurement value was simulated by adding random errors to the true values represented by normally distribution with zero mean and standard deviation.
3.2. Performance Indices
The performance of the algorithm in the simulation studies was obtained by comparing the forecasted and estimated values at time k + 1 with the actual values. The average performance indices for voltage magnitude and voltage angular forecasted and estimated are given as.
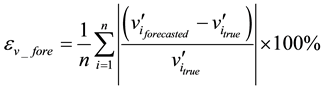
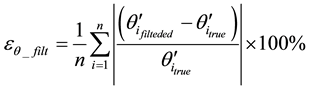
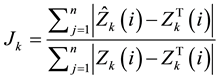
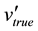


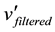
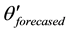

3.3. Results Discussion
In this paper, three test cases are performed, the normal operation, bad data and sudden load change.
Test 1: Normal operation case:
The normal operation case was illustrated by Table 2, Table 3, Figures 1 and 2. Table 2 shows the perfor-
Table 1. The Measurements prepared by the load flow.
Table 2. Performance indices under normal operation.
Table 3. The errors per bus under normal operation.
Figure 1. Performance index under normal operation.
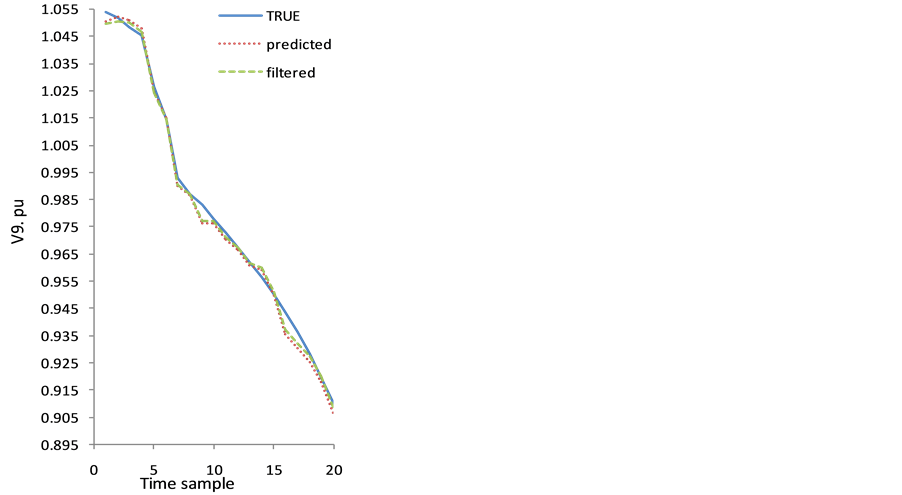
Figure 2. V9 under normal operation.
mance indices of the case. The maximum and average percentage error of voltage magnitudes and angles are made over 20 time sample. From this table, the algorithm has achieved very high performance.
Figure 1 describes the Performance index of the system dynamic nature under normal operation case corresponding to filtered indices calculated at each time sample.
Table 3 shows the percentage for estimated errors per bus for predicted and filtered state with regard to the voltage magnitudes and voltage angles.
In both states, the maximum error occurred in busbar 3 for voltage magnitudes and voltage angles. Furthermore the average errors are equal to the average error in Table 2. Bus 1 is the reference bus, so it is angle is outside of state variables. Figure 3 represents the time behavior for true, forecasted and filtered values of voltage magnitude at bus 9. Figures 3 and 4 show the graphs of the Table 3.
Test 2: Bad data case:
In this test, the simulation was carried out under bad data conditions with three different cases.
・ Single bad data was considered. Active power flow pf(4 - 9) was suspected in error of 10% at the 6th time sample.
・ Two measurements were suspected in error pf(9 - 10) of 20% at the 11th time sample. And also pf(13 - 14) of 50% decrement at the 11th time sample.
・ Single bad data was considered. Reactive power flow qf(4 - 5) was suspected in error of 20% at the 18th time sample.
Suppose that no work is taken to eliminate these errors.
The result of these tests is shown in Tables 4 and 5, Figures 5-7.
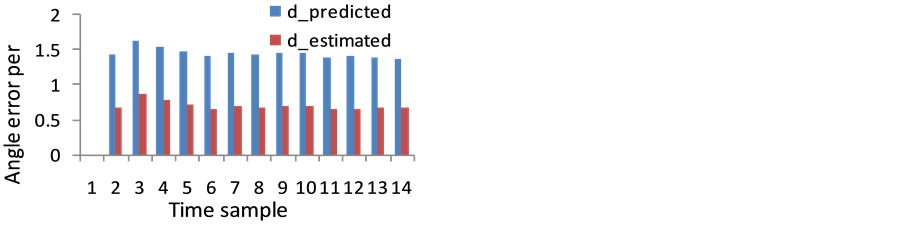
Figure 3. Average voltage error per bus *100%
Figure 4. Average voltage angle error per bur*100%
Table 4. Performance indices under bad data condition.
Table 5. The percentage error per bus under bad data conditions.
Figure 5. Performance index under bad data condition
Figure 6. Average voltage error per bus *100%
Table 4 shows the performance indices of these tests. From this results the average and maximum error becomes larger comparing with normal operation test due to these bad data in measurements.
Figure 5 describes the Performance index of the system dynamic nature under bad data condition’s corresponding to filtered indices calculated at each time sample.
Figures 6 and 7 show the percentage error per bus of the voltage magnitudes and voltage angle’s respectively based on Table 5.
Test 3: Sudden load change:
In the case, the injected load at busbar 3, busbar 9 and busbar 13 are assumed to be sudden changed.
Busbar 3 and busbar 13, 50% of their values are cut at the 6th time sample and 15th time sample respectively. For busbar 9, we assumed that the load is increased to 40% at the 10th time sample.
The result of this case is shown in Tables 6-8, and also shown in Figures 8-10. Table 6 shows the performance indices of the case of sudden load change. From this results the average and maximum error has become difference of normal operation and bad data test due to these changes in load.
Figure 7. Average voltage angle error per bus *100%
Table 6. Performance indices under sudden load change.
Table 7. The percentage error per bus under sudden load change.
Table 8. V13 under sudden load change.
Figure 8. Average voltage error per bus *100%.
Figure 9. Average voltage angle error per bus *100%
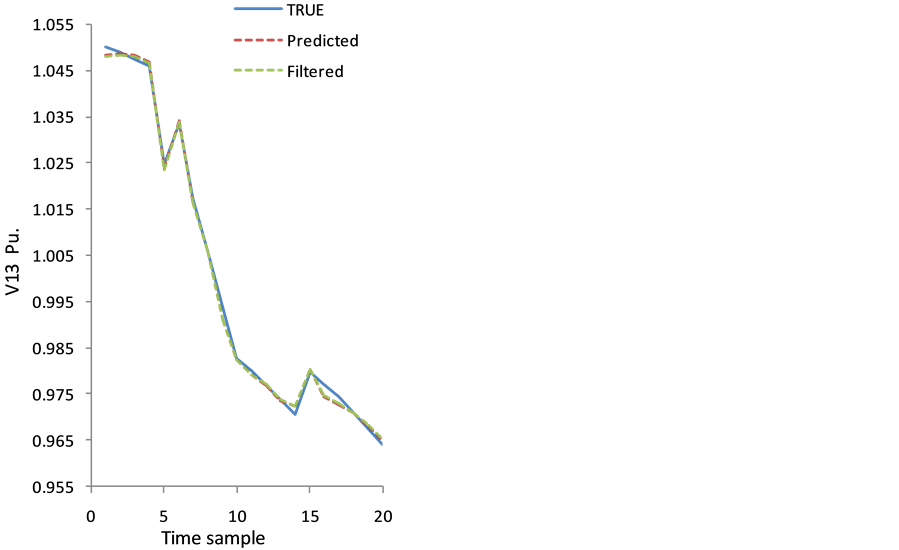
Figure 10. V13 under sudden load change condition.
Figure 10 represents the time behavior for true, forecasted and filtered values of voltage magnitude at busbar 13 based on Table 8. As they are shown in Figure 10, at time sample 6, 10 and 15 when sudden load change, the oscillation in the voltage is appeared very clear.
4. Conclusion
The dynamic state estimator technique has been made based on Holt’s exponential smoothing and Extended Kalman Filter for forecasting and filtering state respectively. The system dynamic was simulated over 20 time samples, with increasing the load at all busbars 5% during any time sample. The algorithm of DSE has been simulated through these 20 time intervals used standard IEEE 14_bus test system under normal and abnormal operation. In this paper, the algorithm gave very good performance results through the normal operation and abnormal operation (bad data and sudden load change) conditions. The error per bus for voltage magnitude and voltage angle has been calculated over these 20 time intervals in both predicted and filtered states.
References
- Shivakumar, N.R. and Jain, A.M. (2008) A Review of Power System Dynamic State Estimation Techniques. Joint In- ternational Conference on Power System Technology and IEEE Power India Conference, New Delhi, 15 October 2008, 1-6.
- Jegatheesa, R. and Leean, K. (1991) Dynamic State Estimation. TENCON’91.1991 IEEE Region 10 International Conference on EC3-Energy, Computer, Communication and Control Systems, New Delhi, 28-30 Aug 1991, 492-496.
- Debs, A.S. and Larson, R.E. (1970) A Dynamic Estimator for Tracking the State of a Power System. IEEE Transac- tions on Power Apparatus and Systems, PAS-89, 1670-1678.
- Jain, A.M. and Shivakumar, N.R. (2008) Phasor Measurement in Dynamic State Estimation of a Power System. TENCON 2008, 2008 IEEE Region 10 Conference, Hyderabad, 19-21 November 2008, 1-6.
- Huang, S.J. and Shih, K.S. (2002) Dynamic-State-Estimation Scheme including Nonlinear Measurement-Function Considerations. Generation, Transmission and Distribution, IEE Proceedings, 149, 673-678.
- Ali, A. and Antonio, G.E. (2004) Power System State Estimation Theory and Implementation. CRC Press, New York.
- Mukhtar, A. (2013) Power System State Estimation. Artech House, London.
- Leite da silva, A.M., Coutto Filho, M.B. and de Queiroz, J.F. (1976) State Forecasting in Electric Power Systems. Generation, Transmission and Distribution, IEE Proceedings C, 130, 79-87.
- Li, H. and Li, W.G. (2009) Estimation and Forecasting of Dynamic State Estimation in Power Systems. International Conference on Sustainable Power Generation and Supply, Nanjing, 6-7 April 2009, 1-6.
- Prajakta, S.K. (2004) Time Series Forecasting Using Holt-Winters Exponential Smoothing. Kanwal Rekhi School of Information Technology, 4329008, 1-13.
- University of Washington Electrical Engineering (1993) Power Systems Test Case Archive. http://www.ee.washington.edu/research/pstca/