Journal of Power and Energy Engineering
Vol.2 No.1(2014), Article ID:42146,8 pages DOI:10.4236/jpee.2014.21001
Dynamic Analysis of a Stand Alone Operation of PEM Fuel Cell System
1Department of Electrical Engineering, Mindanao University of Science and Technology, Cagayan de Oro, Philippines; 2Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, USA.
Email: acultura2003@yahoo.com, ziyad_salameh@uml.edu
Copyright © 2014 Ambrosio B. Cultura, Ziyad M. Salameh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Ambrosio B. Cultura, Ziyad M. Salameh. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received Oct. 4th, 2013; revised Nov. 16th, 2013; accepted Nov. 28th, 2013
Keywords:Dynamic Performance; PEM Fuel Cell
ABSTRACT
In this paper, the dynamic mathematical model of a proton exchange membrane (PEM) fuel cell is presented. Dynamic performance of a PEM fuel cell system by experimental and simulation using matlab/simulink is investigated. The V-I load characteristics of a 1.2 kW PEM fuel cell are presented. Result shows that the starting current of the PEM fuel cell operated at rated load reaches to approximately twice of its rated current in just less than 0.015 second before it reached to its steady state condition. Step change load responses of this PEM fuel cell were experimented and simulated. It was found out, from the results obtained, that PEM fuel cell had a very fast response to load changes. Moreover, results show that the experimental and the result computed by using the simulation of the model are very close to each other which validates the model. Hence, this model could be used to implement a controller design in order to come up with an optimal and efficient operation of PEM fuel cell. Based also on the results, a suitable power conditioning can be constructed and designed for safe and reliable operation of PEM fuel cell especially in integrating and connecting it to a hybrid wind/PV distributed generation system.
1. Introduction
The high price of fossil fuels and the environmental concerns prompted every nation to conduct research on alternative or renewable energy sources such as wind, photovoltaic, micro-hydro, wave, fuel cells, etc. Among these alternative energy sources, fuel cells have been showing up as a highly promising alternative for their high efficiency, ultra low emissions, noise free operation and superior reliability and durability in space, automotive and stand alone applications [1-5]. There are different types of fuel cells depending on the kind of materials used as the electrolyte. The PEM fuel cell with a polymer electrolyte in the form of a thin, permeable sheet has been considered as a promising kind of fuel cell during the last ten years because of its low working temperature, compactness, and easy and safe operational modes. The PEM fuel cell is very simple and uses a polymer as the solid electrolyte and a platinum catalyst [6]. The solid, flexible electrolyte will not leak or crack, and these cells operate at a low enough temperature to make them suitable for homes and cars.
The authors acquired 1.2 kW Ballard PEM fuel cell which was planned to be integrated to the existing distributed generation system that supplied some of the critical loads in the renewable energy laboratory. There is a need to design and develop fuel cell power converter for this specific application. But before doing that, a dynamic characteristic of the PEM fuel cell must be studied and evaluated first in order to safely operate the fuel cell and maximize its performance. To design and control a fuel cell system for the maximum power performance, a designer needs to acquire sufficient knowledge pertaining to the physical process, the internal structure of the process, as well as the dominant input/output variables of the system. In this paper, dynamic models are presented for PEM fuel cells. The real voltage output of a fuel cell is presented. Then, the double layer charging effect is considered and the thermodynamic characteristic inside the fuel cell is integrated into the model according to the energy conservation. A Matlab-Simulink was used to simulate the mathematical model that was presented. Simulation results are given and validated with experimental data both for transient and steady-state responses.
2. PEM Fuel Cell Operating PRINCIPLES
A fuel cell is a device that generates electricity by a chemical reaction. A simplified diagram of PEM fuel cell operating principles is illustrated in Figure 1 [7]. The fuel cell consists of a negative electrode (the anode), a positive electrode (the cathode), and an electrolyte. The hydrogen from a pressurized cylinder enters the anode of the fuel cell and oxygen enters the cathode. Protons and electrons are separated from hydrogen on the anode side. In a basic PEM fuel cell, the protons are transported to the cathode side through the polymer and the electrons are conducted through the load outside the electrode [6].
Hydrogen is the basic fuel, but fuel cells also require oxygen. PEM fuel cells combine hydrogen and oxygen over a platinum catalyst to produce electrochemical energy with water as byproduct. One great appeal of fuel cells is that they generate electricity with very little pollution. A single fuel cell generates a tiny amount of direct current (DC) electricity. In practice, many fuel cells are usually assembled into a stack. Cell or stack, the principles are the same. Fuel gas (in this case pure hydrogen) is transported through the anode towards the anode-electrolyte interface where the following (simplified) oxidation reaction occurs:

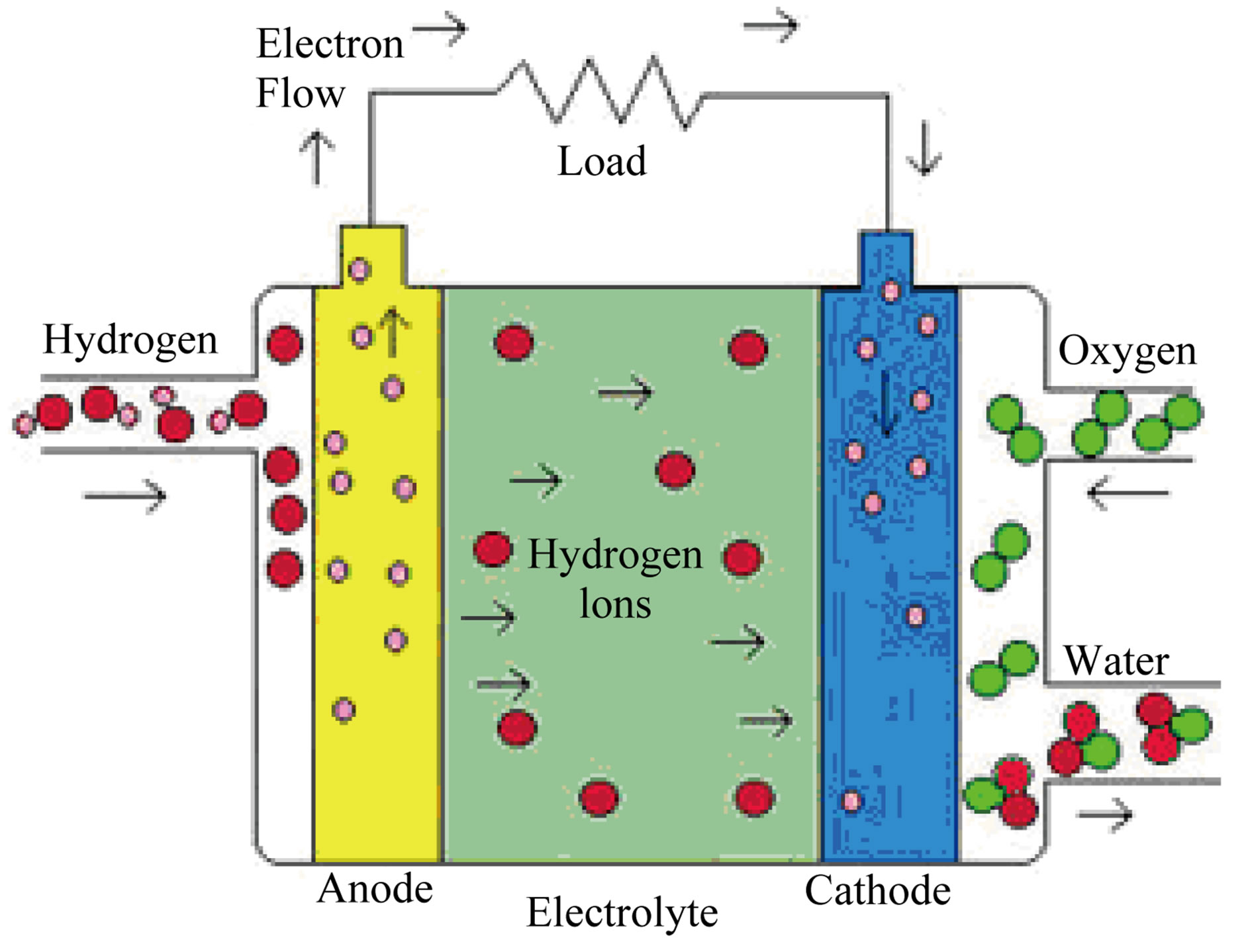
Figure 1. Simplified diagram of the PEM fuel cell operating principles.
The liberated electrons migrate out of the anode and through the external circuit where work is performed, then finally, into the cathode. On the other hand, the positive hydrogen ions (H+) migrate across the electrolyte, towards the cathode, where they ultimately react with oxygen gas and electrons to form water according to:

The overall fuel cell reaction then is simply:
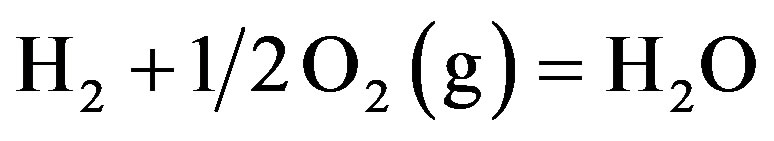
3. PEM Fuel Cell Modeling
In this section, a dynamic model of PEM fuel cell is presented. The real voltage output of a fuel cell is reduced by various over voltage losses namely, activation losses due to reaction kinetics (Vact), ohmic losses from ionic and electronic resistance (Vohm) and concentration losses due to mass transport (Vconc) [1,8]. The voltage of the cell is given in Equation (1).
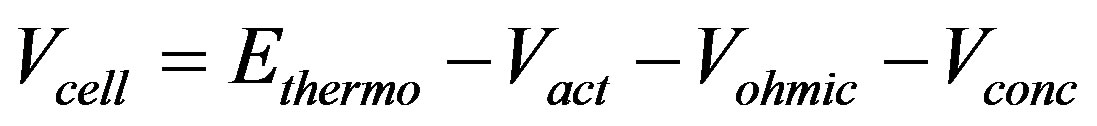 (1)
(1)
And the voltage of the stack is simply the product of the voltage of the cell and the number of cells. (Vstack = Vcell × n)
The (Ethermo) thermodynamically predicted voltage of fuel cell is the potential of the cell obtained in an open circuit thermodynamic balance. It is also called a reversible voltage of the cell (Enermst) whose equation is given by [1-3]
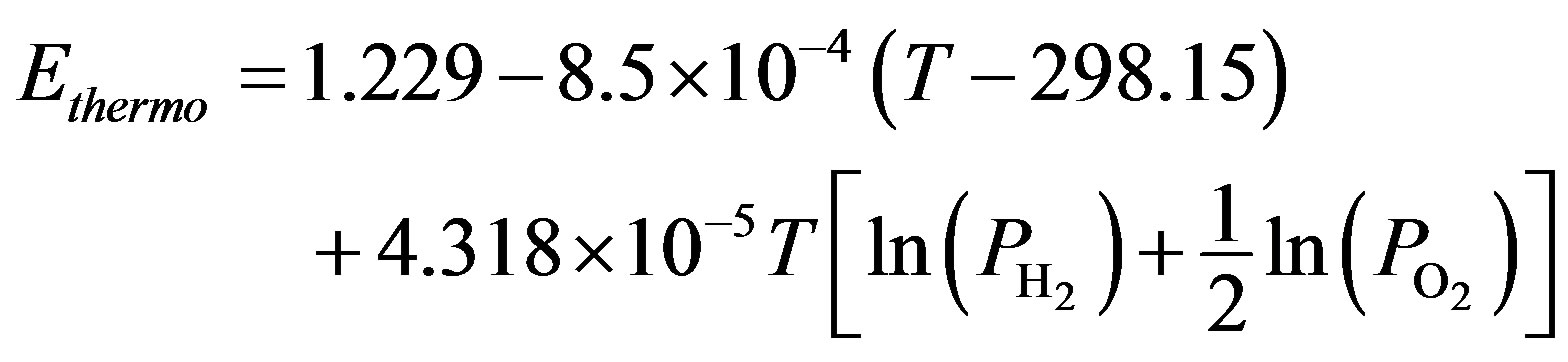 (2)
(2)
The over voltage losses mentioned above are described as polarization, irreversibility which originates primarily from three sources; activation, ohmic and concentration polarization. Figure 2 shows the different regions and the corresponding polarization effects that associated with a voltage drop in every region [1,4,5].
3.1. The Polarization Effects
The three polarization effects mentioned earlier are presented below:
1) Activation Polarization Voltage Drop The active polarization loss is present when the rate of the electrochemical reaction at an electrode surface is controlled by sluggish electrode kinetics [5]. This activation polarization occurs in order to overcome the activation barrier in the electrochemical reactions at the anode and cathode which can be obtained and analyzed by Tafel Equation, presented and used by [2-4,9]:
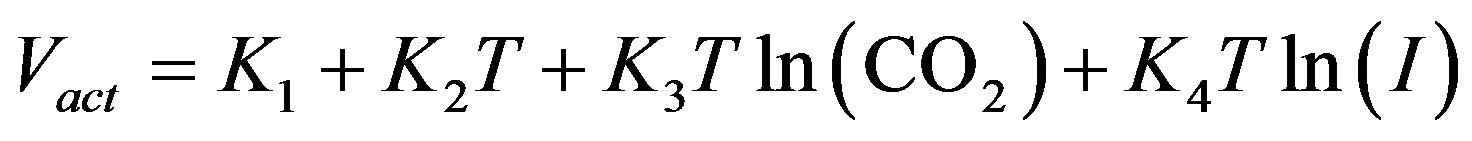 (3)
(3)
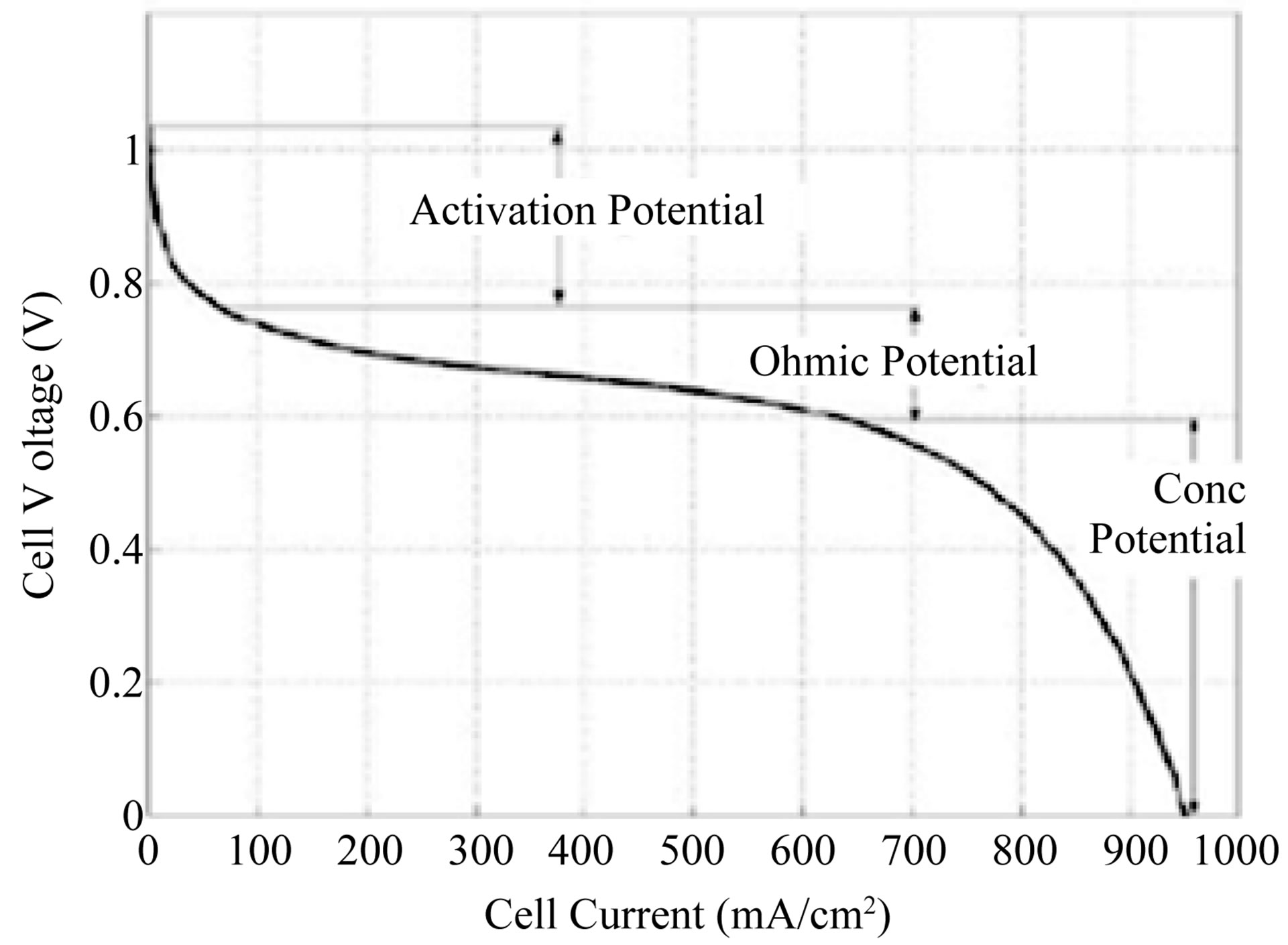
Figure 2. V-I characteristics of a PEM fuel cell.
where: T is the stack temperature (K), I is the operating current density (mA/cm2), CO2 is the concentration of oxygen at the catalyst interface (mol/cm3), and K1, K2, K3 & K4 represent the parametric coefficients based on the experimental data which was published [9,10] for the range of these values as follows: K1 = -0.948 ± 0.004, K2 = 0.00312, K3 = 6.8 ± 0.2 × 10-5, K4 = -1.97 ± 0.05 × 10-4. In the simulation, the following parametric coefficients are used; K1 = -0.9514, K2 = 0.00312, K3 = 7.4 × 10-5, K4 = -1.87 × 10-4.
The CO2 is the oxygen concentration which is a function of stack temperature, whose equation given by [4]
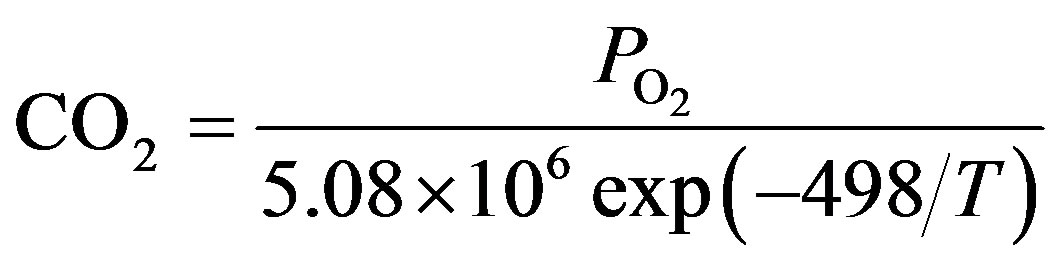 (4)
(4)
2) Ohmic Polarization Voltage Drop Ohmic polarization associated with the conduction of ions and electrons. The ohmic polarization varies directly with current, increasing over the entire range of current because cell resistance remains essentially constant. Ohmic losses occur because of the resistance due to the electrons transfer between electrodes and the ions travel through the solid polymer membrane. The ohmic losses presented with an equivalent resistance (Rohm) and this resistance causes the voltage loss that obeys Ohm’s Law. The ohmic polarization can be expressed in equation below [4]:
 (5)
(5)
where:
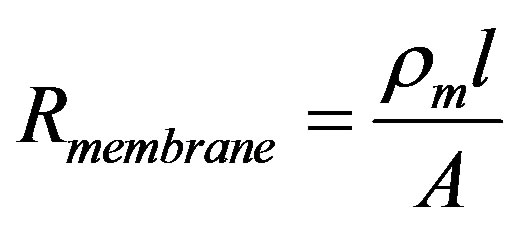
The following empirical expression for membrane resistivity was proposed by [7]
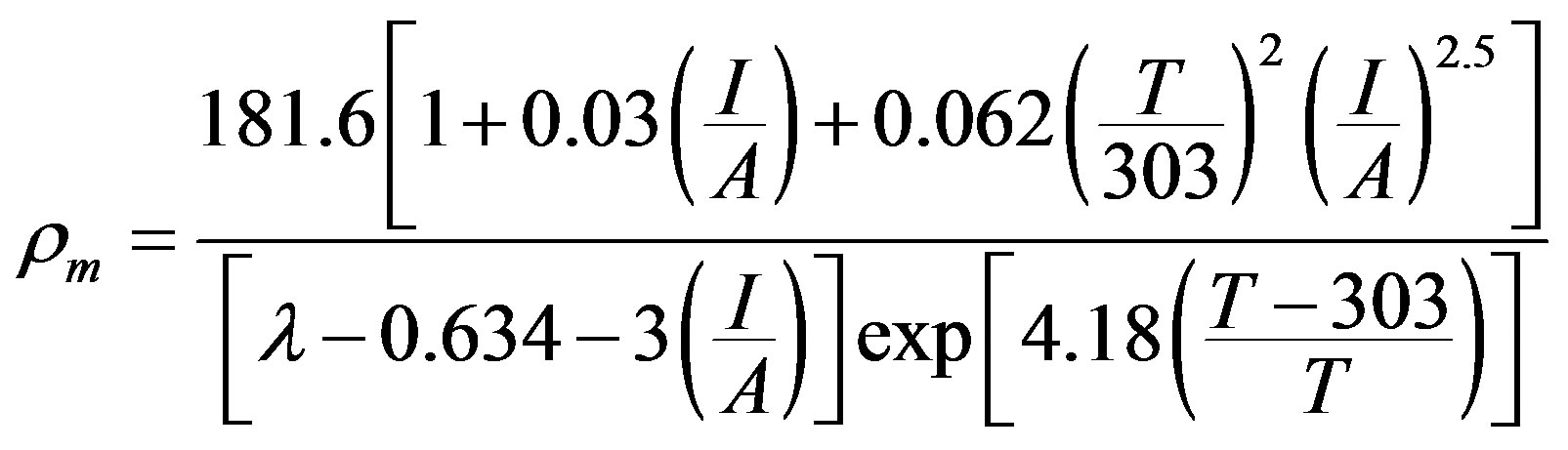 (6)
(6)
The parameter λ will be influenced by the membrane preparation procedure, a function of the relative humidity and stoichiometric ratio of the anode and cathode feed gases and a function of the age and thermal hydration history of the membrane [6,7,11]. In previous study [6,7] λ is being considered as an adjustable fitting parameter, commonly between 10 and 23 which is also being considered in this paper. A value of the order of 14 under ideal conditions of 100% of relative humidity and there are values reported in the order of 22 and 23 under over saturated conditions [1,3].
3) Concentration Polarization Voltage Drop The transport of gas and liquid is included in this loss. Within the electrolyte layer, the depletion of reactants and the accumulation of the product affect significantly the FC performance. Mass transport losses occur over the entire range of current density, but these losses become prominent at high limiting currents where it becomes difficult to provide enough reactant flow to the cell reaction site. Several processes contribute to concentration polarization but slow transport of reactants and products to and from the electromechanical reaction site is a major contributor to concentration polarization [Nam thesis]. The concentration polarization voltage drop is defined as [Nam thesis]:
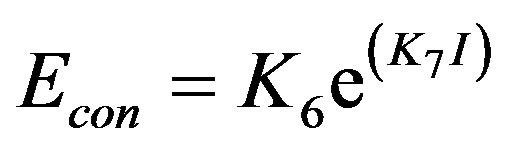 (7)
(7)
where: K6 and K7 are coefficients and are given as [12]:
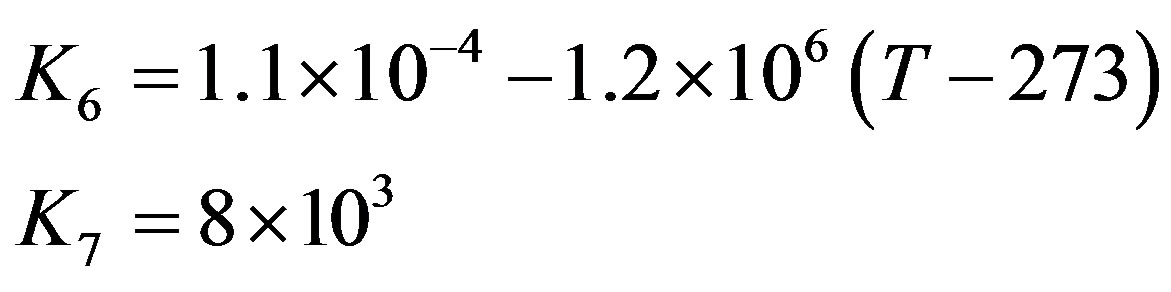
3.2. The Charge Double Layer Effect
The double layer charging effect occurs due to the diffusion and the reaction between the electrons and the ions, there is charge double-layer around the cathode in a fuel cell. The layer of charge on or near the electrode interface behaves much like an electrical capacitor [10]. The result is that if the current suddenly changes, the operating voltage takes some time to arrive its final equilibrium value. This effect of double layer capacitance charging can be expressed by Equation (7) [4]:
 (8)
(8)
3.3. The Conservation Equations
The instantaneous conditions inside the cell can be determined through the ideal gas equations using the following formulas given by [4,10,13];
Anode Mole Conservation:
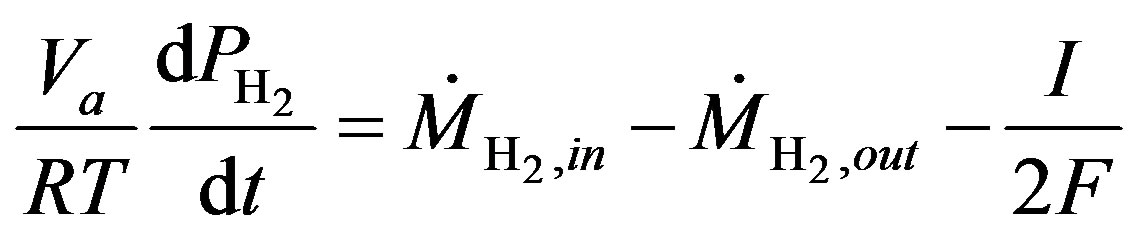 (9)
(9)
where:
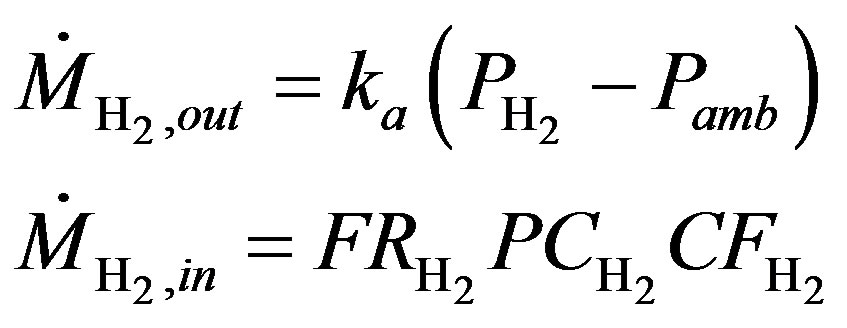
Cathode Mole Conservation:
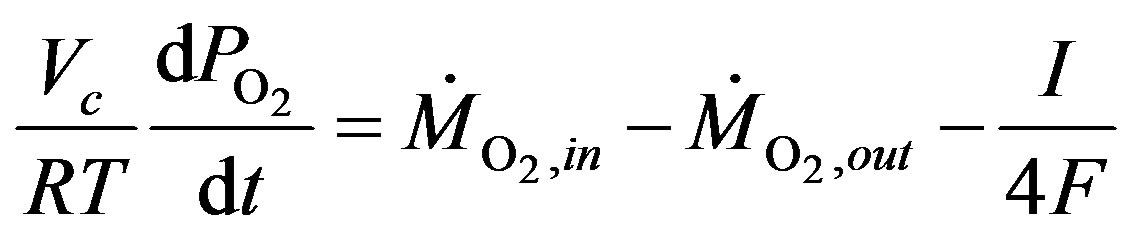 (10)
(10)
where:
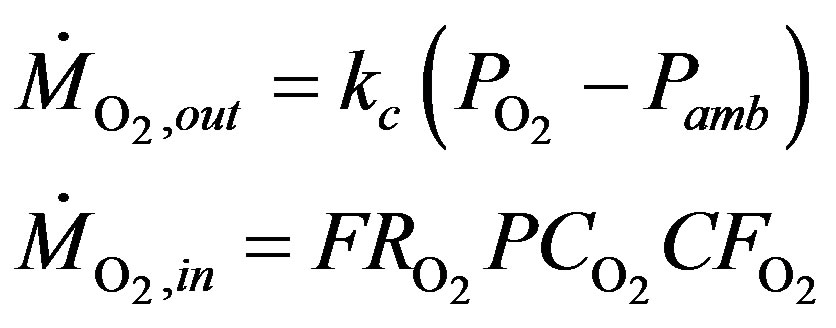
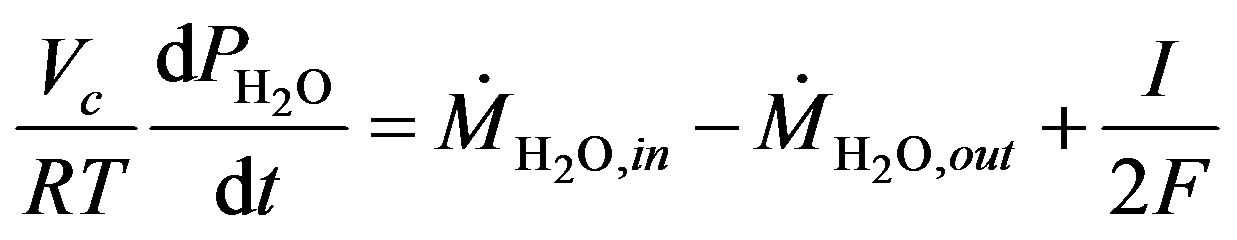 (11)
(11)
where:

4. Evaluation Station and Data Acquisition System
The authors designed and fabricated the evaluation station of a PEM Fuel Cell for stand alone applications illustrated in the block diagram as shown in Figure 3. This station is used to test, control and monitor the operation of a PEM fuel cell. Figure 4 below is the picture of the actual set up of the PEM fuel cell evaluation station installed at the renewable energy laboratory of Umass Lowell. The system consists of PEM fuel cell, load relay, circuit protection, diodes, dc load, sensors, data acquisition and personal computer. Fuel cell current flows through the 60 A circuit breaker and passing through 2 - 30 A diode before going to the load. The purpose of the diode is to prevent a surge current flowing from load or battery back to the fuel cell. The dc load (dynaload) is used to discharge energy from the fuel cell. Load current flows from fuel cell passing through a 60 A circuit protection and going to the dc load (dynaload). Sensors (for current, voltage and temperature) were installed and used to measure the output data which passed the signal input to conditioning circuit before sending it to the data acquisition.
The 1.2 kW Ballard PEM fuel cell has its own built-in data acquisition that logs internal parameters of PEM fuel cell. This is connected to the personal computer in order to save all the measured parameters (like stack voltage and current, temperature, etc.) of the fuel cell during operation. The author installed another data acquisition in order to monitor the load voltage & load current and save the data in the hard drive of the computer. During the evaluation, output data will be collected through the NI USB DAQ and will be automatically saved in the hard drive of the computer using a LabView software program. Figure 5 is the block diagram of the DAQ LabView program that automatically save the measured load output data to the hard disk.
5. Simulation and Experimental Results
In order to predict the performance of the PEM fuel cell, a computer simulation has been implemented using Matlab/Simulink. The values of the fuel cell model parameters used in the simulation are presented in Table 1. Based on the mathematical models of PEM fuel cell presented in Section 3, a Matlab/Simulink whole block diagram was built and presented in Figure 6. The system contains the following subsystems namely; fuel cell, hydrogen, oxygen and water flow, and load subsystems. The load considered in the simulation is a resistive load. The PEM fuel cell was simulated in order to examine the dynamic performance during starting and in load change condition. The differential equations have been solved using the ode23s solver method as provided in Matlab/Simulink software package. The scope blocks were

Figure 3. Fuel cell tester block diagram.

Figure 4. Fuel cell station at umass lowell.
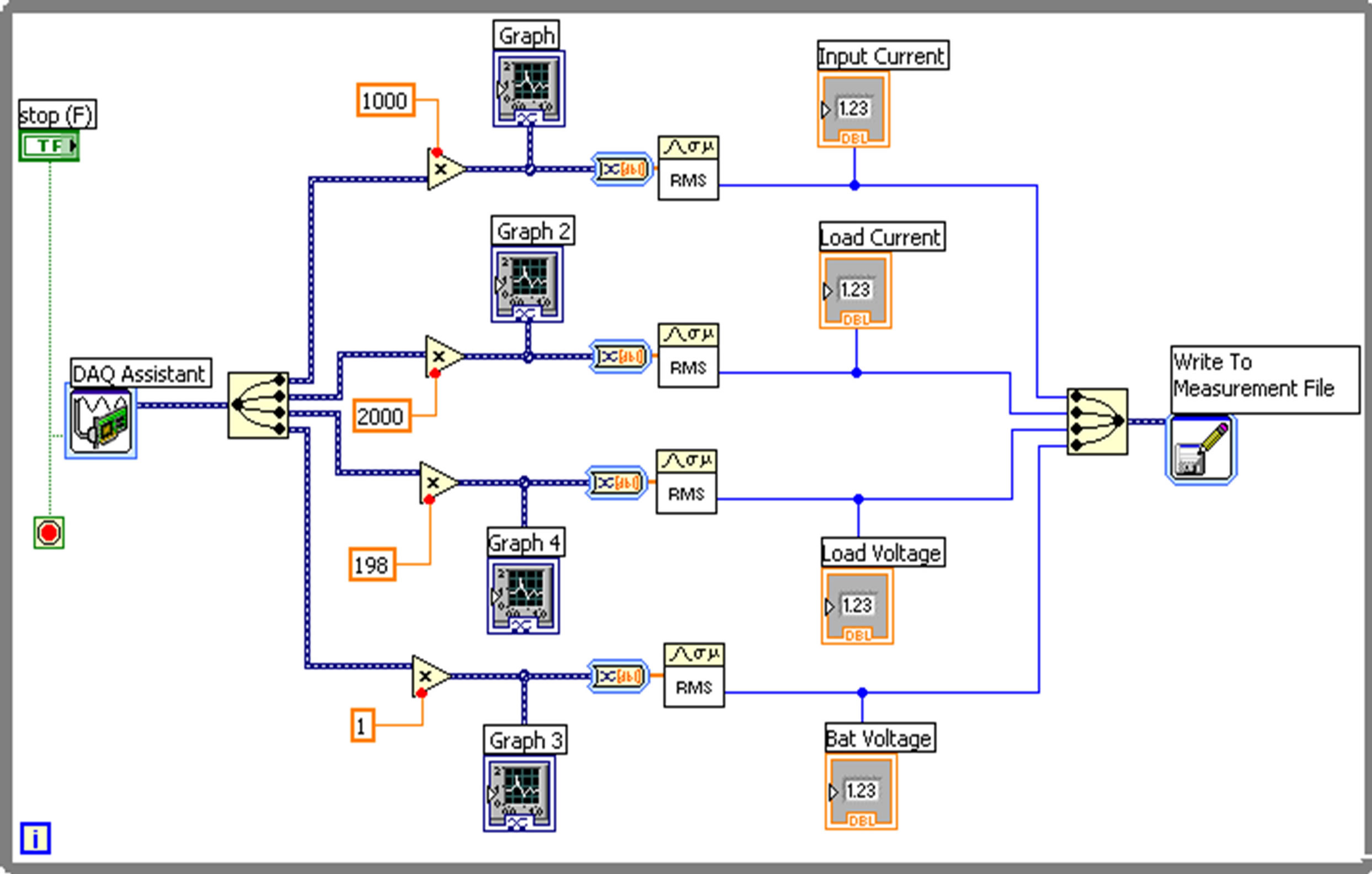
Figure 5. DAQ LabVIEW block diagram.
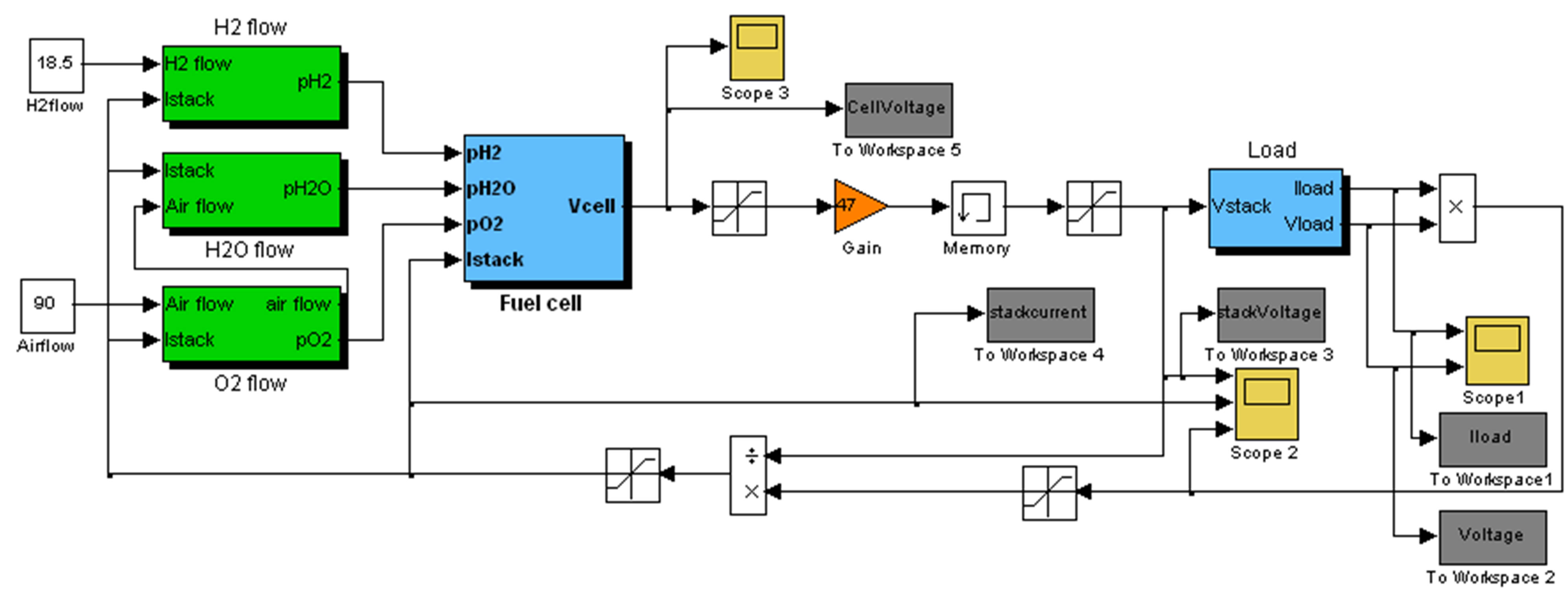
Figure 6. Simulink block diagram for load connected PEM fuel cell.

Table 1. Fuel cell model parameters used in the simulation.
installed in order to visualize the output graph of the simulation. The To Workspace block is connected in parallel to the scope in order to transport data to the mathlab.m files for easy plotting of the simulation and experimental results.
The starting transient response of the cell voltage of PEM fuel cell at different load current is presented in Figure 7. It was observed that the settling time decreases as the load current sets to a higher value. At rated load, the cell voltage goes to as high as 1.229 V and goes down to a steady state of 0.58 V very quickly in just 0.015 second while the stack current went up to as high as 95 A and settled down to a steady state of 46 A very quickly in less than 0.015 second.
The transient response of the load voltage, current and power of a 1.2 kW PEM fuel cell is presented in Figures 8 and 9. It was observed that at rated load the current reaches to 95 A and it stabilizes to 45.84 A while the voltage goes up to 55 V and stabilizes to 26.81 volts in just 0.015 second.
Figure 10 below is the graph of the load voltage versus load current output of the PEM fuel cell. Simulation and experimental results of the voltage-current characteristics show almost the same or very close to each other. A slight difference may cause in reading and logging the data. Hence, this shows that experimental result validates the model that was simulated.
The simulation and experimental responses of the commercial fuel cell module to step change in load are

Figure 7. Cell voltage transient behavior of PEM fuel cell.

Figure 8. Simulated load voltage and current transient behavior of a 1.2 kW PEM fuel cell.
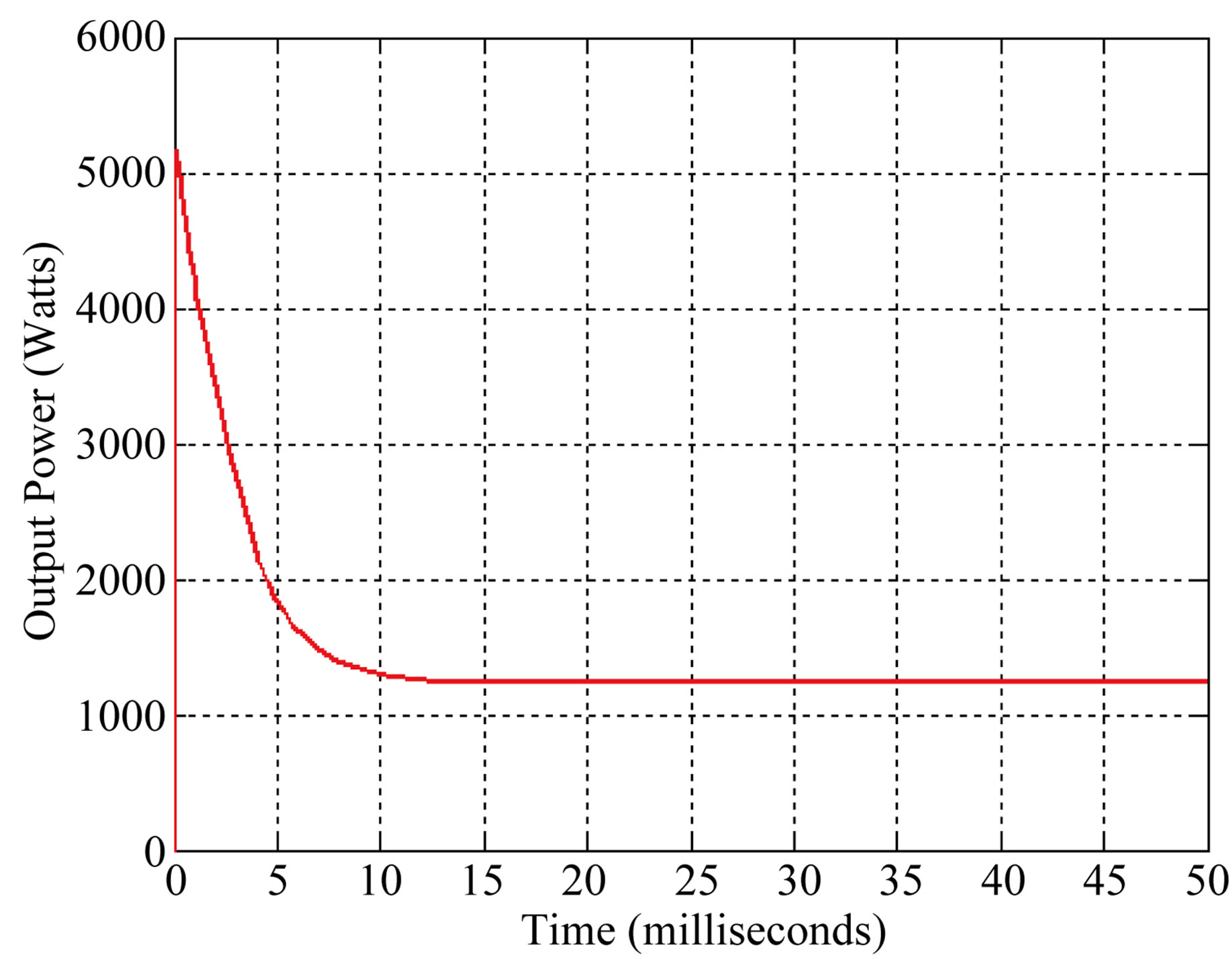
Figure 9. Simulated power output transient behavior of a 1.2 kW PEM fuel cell.
shown in Figures 11 and 12. Figure 11 shows the graphs of simulation and experimental results at step up change
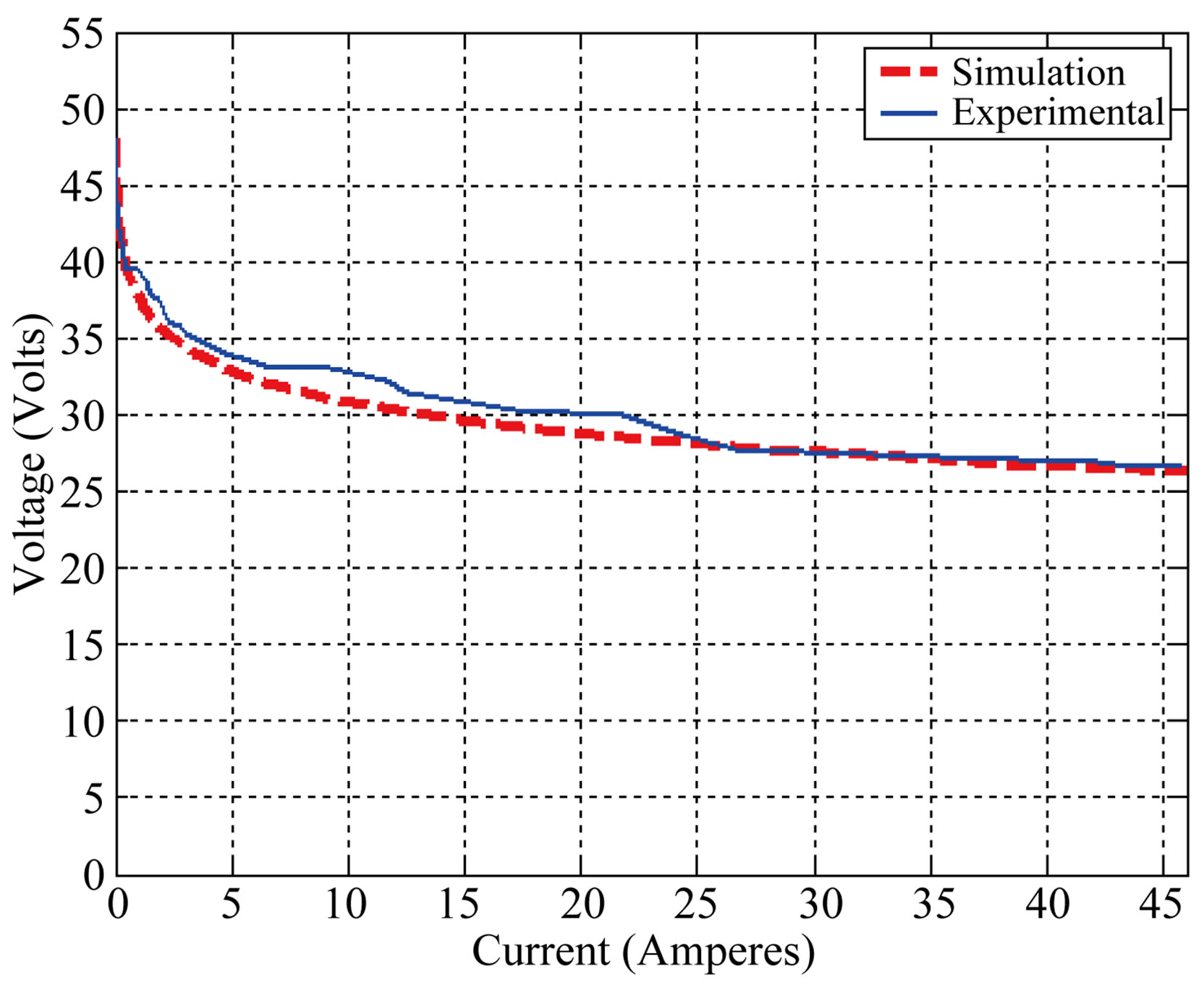
Figure 10. V-I load characteristics of a 1.2 KW PEM fuel cell.
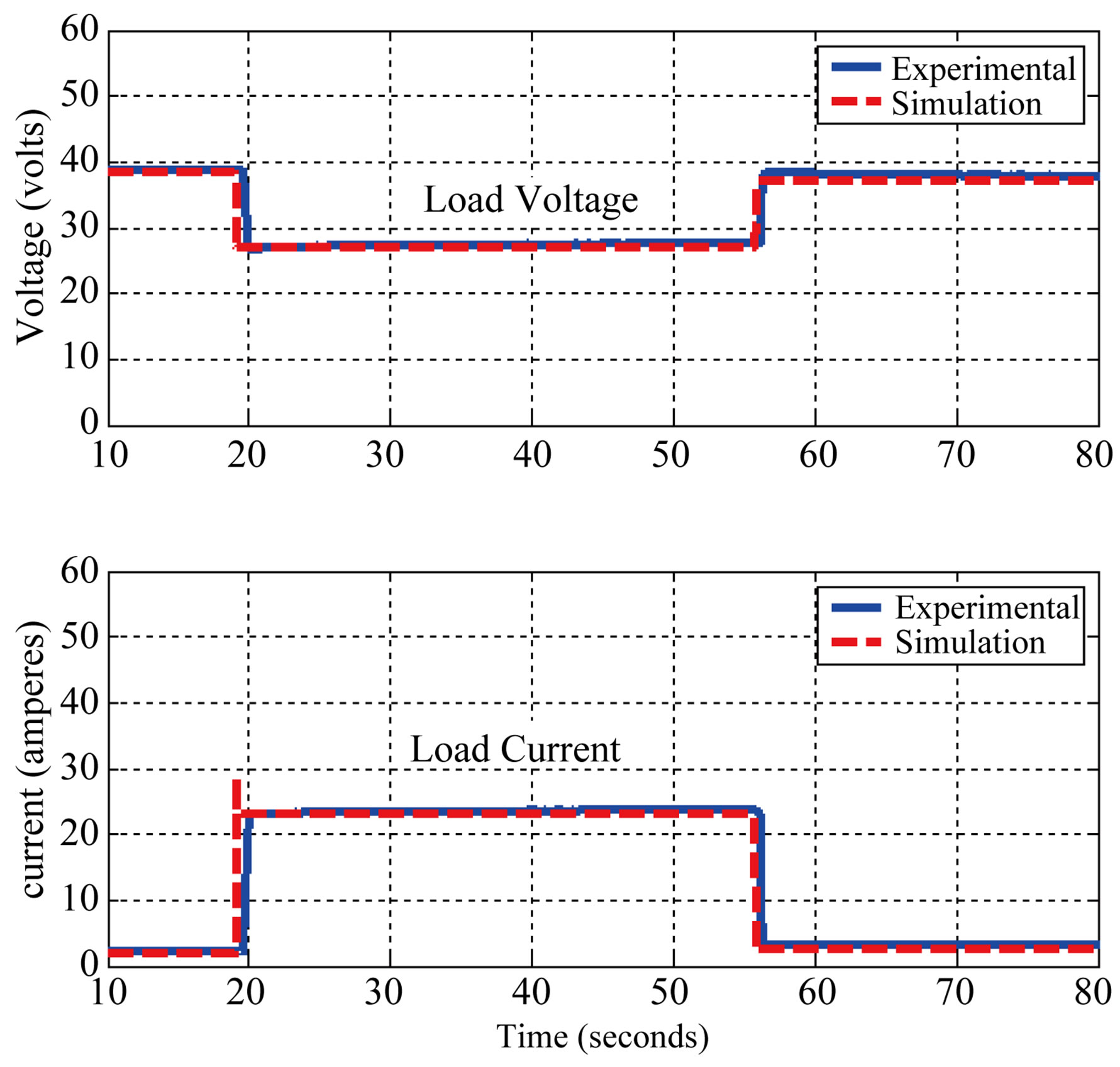
Figure 11. Step up load variation of PEM fuel cell.
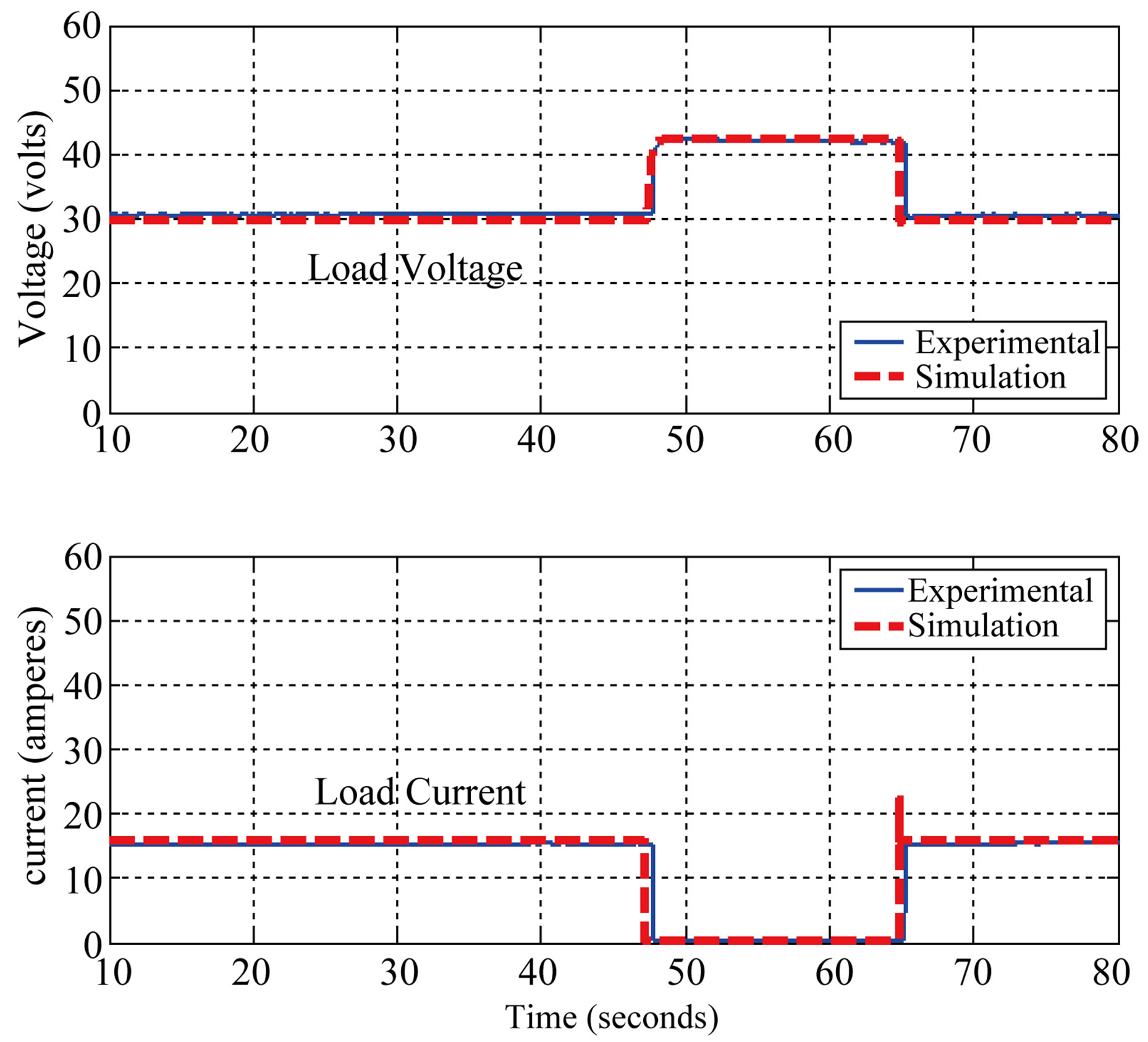
Figure 12. Step down load variation of PEM fuel cell.
of the load current from 1.67 A to 23.08 A, while load voltage drops correspondingly from 38.34 V to 26.74 V.
Figure 12 shows the graphs of simulation and experimental results when the step down change of the load current from 15.3 A to 0.08 A was implemented, the load voltage suddenly increase from 30.5 V to 42.25 V at the same time as load current drops. These curves show that the experimental result and the result computed using the simulation of the model are very close to each other which validates the model.
6. Conclusion
This paper has presented a dynamic mathematical model of PEM fuel cell. Simulation using Matlab/Simulink and experimental results were presented by comparing the outputs. The dynamic and step change load response of a PEM fuel cell was presented and analyzed. It was observed from the obtained results that PEM fuel cell had a very fast response to load changes. Moreover, the model has been validated on actual operation of PEM fuel cell, showing that the simulated results in Matlab/Simulink are consistent with the experimental results. Hence, this model can be used to implement a controller design in order to come up with an optimal and efficient operation of PEM fuel cell which is the next potential research to undertake. Based also on this model, a suitable power conditioning can be constructed and designed for efficient and reliable operation of PEM fuel cell which the authors plan in integrating to the existing PV/Wind hybrid distributed generation.
REFERENCES
- J. M. Correa, F. A. Farret and L. N. Canha, “An Analysis of the Dynamic Performance of Proton Exchange Membrane Fuel Cells,” Proceedings of 27th Annual Conference of the IEEE Industrial Electronics Society, Denver, 29 November-2 December 2001, pp. 141-146.
- K. Xin and A. M. Khambadkone, “Dynamic Modelling of Fuel Cell with Power Electronics Current and Performance Analysis,” IEEE International Conference on Power Electronics and Drive Systems, Vol. 1, 2003, pp. 607-612.
- Q. L. Yu, A. K. Srivastava, S.-Y. Choe and W. Z. Cao, “Improved Modeling and Control of a PEM Fuel Cell Power System for Vehicles,” Proceedings of the IEEE SoutheastCon, Memphis, 31 March-2 April 2006, pp. 331-366.
- M. J. Khan and M. T. Iqbal, “Dynamic Modelling and Simulation of a Fuel Cell Generator,” Faculty of Engineering and Applied Science, Memorial University of Newfoundland, St. John’s, 2005.
- D. C. Yu and S. Yuvarajan, “A Novel Circuit Model for PEM Fuel Cells,” Proceedings of IEEE APEC, Vol. 1, 2004, pp. 362-366.
- R. F. Mann, J. C. Amphlett, M. A. I. Hooper, H. M. Jensen, B. A. Peppley and P. R. Roberge, “Development and Application of a Generalized Steady-State Electrochemical Model for a PEM Fuel Cell,” Elsevier Science S.A., México City, 2000.
- http://americanhistory.si.edu/fuelcells/basics.htm#q1
- R. O’Hayre, S.-W. Cha, W. Collea and F. B. Prinz, “Fuel Cell Fundamentals,” John Wiley & Sons, Inc., Hoboken, 2006.
- M. W. Fowler, R. F. Mann, J. C. Amphlett, B. A. Peppley and P. R. Roberge, “Incorporation of Voltage Degradation into a Generalized Steady State Electrochemical Model for a PEM Fuel Cell,” Elsevier Science B.V., Holland, 2002.
- C. Wang, H. Nehrir and S. R. Shaw, “Dynamic Models and Model Validation for PEM Fuel Cells Using Electrical Circuits,” IEEE Transactions on Energy Conversion, Vol. 20, No. 2, 2005, pp. 442-451. http://dx.doi.org/10.1109/TEC.2004.842357
- P. Famouri and R. S. Gemmen, “Electrochemical Circuit Model of a PEM Fuel Cell,” IEEE Transactions, Vol. 3, 2003, pp. 1436-1439.
- L. J. M. J. Blomen and M. N. Mugerwa, “Fuel Cell Systems,” Plenum Press, New York, 1993.
- P. Buasri and Z. Salameh, “An Electrical Circuit Model for a Proton Exchange Membrane Fuel Cell (PEMFC),” Annual IEEE PES, Montreal, 2006, PP. NO. 06GM0394.
Nomenclature
Vcell: Operating voltage of fuel cell (V)
Ethermo: Thermodynamically predicted voltage of PEM fuel cell (V)
Vact: Activation voltage (V)
Vohm: Ohmic voltage (V)
Vconc: Concentration voltage (V)
I: Cell current density (mA/cm2)
Ract: Activation resistance (kΩ×cm2)
Rmembrane: Membrane resistance (kΩ×cm2)
Vstack: Stack voltage (V)
Istack: Stack current (Amp)
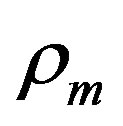 : Specific resistivity for the flow of hydrated protons (ohm-cm)
: Specific resistivity for the flow of hydrated protons (ohm-cm)
l: Thickness of the polymer membrane (cm)
A: Cell active area (cm2)
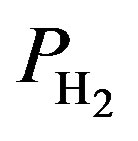 : Hydrogen pressure (atm)
: Hydrogen pressure (atm)
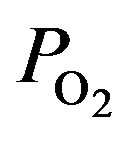 : Oxygen pressure (atm)
: Oxygen pressure (atm)
CO2: Oxygen concentration (mol/cm3)
R: Universal Gas Constant (J/molK)
F: Faraday Constant (C/mol)
T: Stack Temperature (K)
P: Cell Pressure (atm)
Cd: Double Layer Capacitance (F)
Pamb: Ambient Pressure (atm)
Va: Anode Volume (m3)
ka: Anode Flow Constant (mol/s-atm)
Vc: Cathode volume (m3)
kc: Cathode Flow Constant (mol/s-atm)
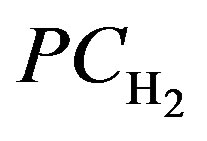 : Percentage of H2 purity
: Percentage of H2 purity
 : Hydrogen Flow Rate Conversion Factor
: Hydrogen Flow Rate Conversion Factor
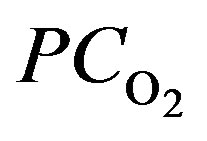 : Percentage of O2 purity
: Percentage of O2 purity
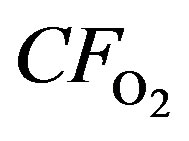 : Oxygen Flow Rate Conversion Factor
: Oxygen Flow Rate Conversion Factor
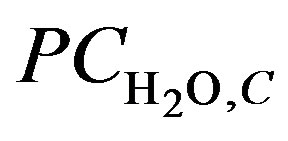 : Cathode Vapour Content n: Number of cells
: Cathode Vapour Content n: Number of cells
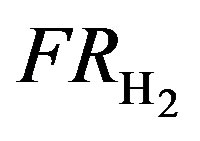 : Hydrogen flow rate (SLPM)
: Hydrogen flow rate (SLPM)
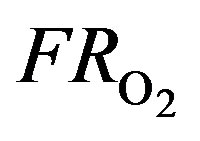 : Oxygen flow rate (SLPM)
: Oxygen flow rate (SLPM)
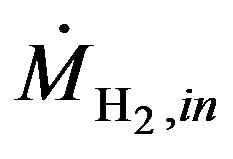 : Hydrogen inlet flow rate (mol/s)
: Hydrogen inlet flow rate (mol/s)
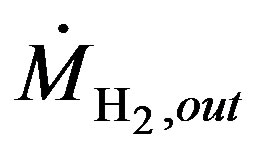 : Hydrogen outlet flow rate (mol/s)
: Hydrogen outlet flow rate (mol/s)
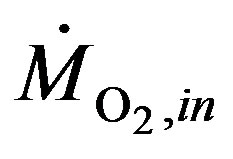 : Oxygen inlet flow rate (mol/s)
: Oxygen inlet flow rate (mol/s)
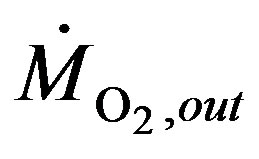 : Oxygen outlet flow rate (mol/s)
: Oxygen outlet flow rate (mol/s)
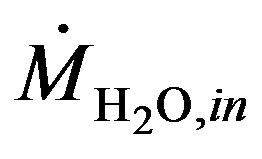 : Cathode vapour inlet flow rate (mol/s)
: Cathode vapour inlet flow rate (mol/s)
 : Cathode vapour outlet flow rate (mol/s)
: Cathode vapour outlet flow rate (mol/s)
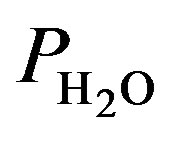 : Cathode vapour pressure (atm)
: Cathode vapour pressure (atm)

