Journal of Materials Science and Chemical Engineering
Vol.04 No.03(2016), Article ID:64344,9 pages
10.4236/msce.2016.43001
Study of Frequency Effects on Hardness Profile of Spline Shaft Heat-Treated by Induction
Habib Hammi, Abderazzak El Ouafi*, Noureddine Barka
Mathematics, Computer Science and Engineering Department, University of Quebec at Rimouski, Rimouski, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 January 2016; accepted 6 March 2016; published 9 March 2016
ABSTRACT
This paper is devoted to the study of frequency effects on hardness profile of AISI 4340 spline shaft heat-treated by induction through an extensive 3D finite element method simulation and structured experimental investigation. Based on coupled electromagnetic and thermal fields analysis, the 3D model is used to estimate the temperature distribution and the hardness profile. The proposed study examines the hardening process parameters, such as frequency, induced current density and heating time, known to have an influence on hardened surface and builds the simulation model step by step. The established model can provide not only an accurate prediction of temperature distribution and hardness profile but also a comprehensive analysis of machine parameters effects, especially the frequency. The numerical results achieved by this model are good and present a great agreement to the experimental data.
Keywords:
Induction Heating, Splines Shaft, Hardness Profile, Current Density, Heating Time, Frequency

1. Introduction
Surface transformation hardening processes are designed to improve wear and fatigue resistance by hardening the superficial critical areas using brief and localized heat gains. Among these processes, induction heating process is well-known by its capacity in terms of high power density which allows short interaction times to reach the required temperature, while limiting the risks of undesirable distortion and deformation effects [1] [2] . Induction heating consists of heating an electrically conducting part by applying an alternative current at a specific frequency into a copper coil to produce a variable electromagnetic field, which generates induced eddy currents in the region, close to the coil. The eddy currents flowing through the resistance of the part, placed within the coil, heat it by Joule effect. The induction heating process exhibits several industrial advantages: i) requires low energy levels; ii) minimizes distortion and deformation of the heated parts; iii) easily to integrate in automated production lines and iv) considered as a sustainable manufacturing process [1] [2] . The mechanical characteristics of the hardened surface obtained by this process depend on the physicochemical properties of the treated material and several induction heating parameters and conditions. To be able to appropriately use the resources offered by an induction heating system, it is necessary to develop a comprehensive strategies to control the heating process parameters in order to produce desired hardened surface characteristics for a specific application. Despite some attempts to develop models and approaches to study typical aspects of the induction heating, the developed simulation tools and strategies are not flexible enough to be applied to various materials and geometries [3] - [5] . Current practices in the industry are based on the control the induction heating process using handbook data and the traditional and fastidious trial and error procedures for every single specific mechanical component. There are no general studies that document and predict the performance of the process as function of heating system parameters.
The efficiency of an induction heating system for typical application depends on several factors such as characteristics of the mechanical part itself (material and geometry), inductor design and heating system parameters (power supply capacity, frequency, induced current density, heating time, etc.) [2] - [6] . It is very well known that the penetration depth is proportional to the inverse of the frequency, leading to a comprehensive study of the difference between using a high frequency (HF) and medium frequency (MF) current in the heating process. Furthermore, to obtain an adequate temperature distribution and uniform hardness profile, in the case of the spline shaft treatment, a specific frequency is required to qualify the induced current to reach the tooth and the root zones. Relationship between the resulting temperature and the frequency used has to be established.
In this work, a coupled electromagnetic fields and thermal analysis 3D numerical model for AISI 4340 steel spline shaft is designed using COMSOL multi-physics software. Various induction heating parameters such as frequency, induced current density and heating time are tested and their effects on temperature distribution and hardness profile are evaluated. The 3D model subsequently used specifically to establish and evaluate the contribution of the frequency variation on the heating process performance. The numerical results achieved by the 3D model are validated using relevant experimental data.
2. Problem Formulation and Simulation
The proposed simulation 3D model uses a 25 mm external diameter AISI 4340 steel spline with 21 mm internal diameter. The spline is wound with a 27 mm copper based coil (Figure 1). Because of the circular symmetry of the shaft, only one twelfth of the spline and the coil are considered in the simulation model (the spline is com- posed of twelve teeth). These parameters are chosen taking into account the constraints imposed by the experimental setup and conditions (heating system and geometry of the available mechanical parts). The AISI 4340 alloy steel used is a low alloy steel that contains iron (95.195% - 96.33%), nickel (1.65% - 2%), chromium (0.7% - 0.9%), manganese (0.6% - 0.8%), carbon (0.37% - 0.43%), molybdenum (0.2% - 0.3%), silicon (0.15% - 0.3%), sulfur (0.04%) and phosphorous (0.035%). This steel is heat treated at 830˚C followed by quenching in
Figure 1. Schematic representation of 3D model.
oil. The analysis assumes that the ambient temperature is set to 293 K and that the spline and the coil are surrounded by a local dielectric environment that is magnetically isolated with vacuum permittivity and permeability.
2.1. Problem Formulation
To calculate the electromagnetic field, it is imperative to solve Maxwell’s equations, for generally varying electromagnetic fields. Maxwell’s equations can be written as:
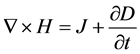 (1)
(1)
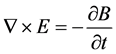 (2)
(2)
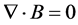 (3)
(3)
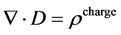 (4)
(4)
Here E is electric field intensity, D is electric flux density, H is magnetic field intensity, B is magnetic flux density, J is conduction current density, and 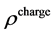 is electric charge density. Special symbols like
is electric charge density. Special symbols like  and
and  are popular in vector algebra and are useful to shorten an expression of particular differential operations
are popular in vector algebra and are useful to shorten an expression of particular differential operations
without having to carry out the details. 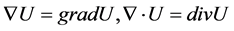 and
and . In this part, we used the Fourier equation as it is written in the following form.
. In this part, we used the Fourier equation as it is written in the following form.
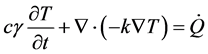 (5)
(5)
T is temperature, 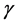 is the density of the metal, c is the specific heat, k is the thermal conductivity of the metal and Q is the heat source density induced by eddy currents per unit time in a unit volume. So the system to be solved is given by:
is the density of the metal, c is the specific heat, k is the thermal conductivity of the metal and Q is the heat source density induced by eddy currents per unit time in a unit volume. So the system to be solved is given by:
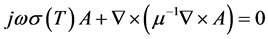 (6)
(6)
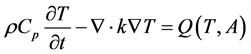 (7)
(7)
where 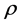 is the density,
is the density, 
Induction heating is a non-contact heating process. It uses high frequency electricity to heat materials that are electrically conductive [6] . Since it is non-contact, the heating process does not contaminate the material being heated. It is also very efficient since the heat is actually generated inside the work piece. This can be contrasted with other heating methods where heat is generated in a flame or heating element, which is then applied to the work piece.
A source of high frequency electricity is used to drive a large alternating current through a coil [7] . This coil is known as the work coil. The passage of current through this coil generates a very intense and rapidly changing magnetic field in the space within the work coil. The work piece to be heated is placed within this intense alternating magnetic field [6] , [8] . The alternating magnetic field induces a current in the conductive work piece. The arrangement of the work coil and the work piece can be thought of as an electrical transformer. The work coil is like the primary where electrical energy is fed in, and the work piece is like a single turn secondary that is short-circuited. This causes tremendous currents to flow through the work piece, known as eddy currents.
In addition to this, the high frequency used in induction heating applications gives rise to a phenomenon called skin effect [6] and [9] . This skin effect forces the alternating current to flow in a thin layer towards the surface of the work piece. The skin effect increases the effective resistance of the metal to the passage of the large current. Therefore it greatly increases the heating caused by the current induced in the work piece. The principle of induction heating is mainly based on two well-known physical phenomena.
The energy transfer to the object to be heated occurs by means of electromagnetic induction. It is known that in a loop of conductive material an alternating current is induced when this loop is placed in an alternating magnetic field. The following formula defines the induced voltage, E, as the change of flux magnetic (

When the loop is short-circuited, the induced voltage (E) will cause a current to flow that opposes its cause, the alternating magnetic field. This is Faraday-Lenz’s law.
If a “massive” conductor (e.g. a cylinder) is placed in the alternating magnetic field instead of the short circuited loop, eddy currents (Foucault currents) will be induced within it. The eddy currents heat up the conductor according to the Joule effect.
The second phenomena is the Joule effect, wherein a current, I(A) flows through a conductor with a resistance, 


A general characteristic of alternating currents is that they are concentrated on the outside of a conductor. This is called the skin effect. Eddy currents induced in the material are also the biggest on the outside and diminish towards the center [10] . Therefore most of the heat is generated on the outside. The skin effect is characterized by its so-called penetration depth (


The penetration depth depends on the characteristics of the material to be heated (

On the contrary, ferromagnetic materials (iron, many types of steel) have a relative magnetic permeability that is much higher. Therefore, these materials generally show a more explicit skin effect (smaller


where, 

2.2. Simulation
Simulations were conducted after establishing the most suitable mesh size to be used. The imposed current density (


3. Effect of Frequency and Heating Time on Temperature Distribution
Five frequencies are used in this work: 50 kHz, 100 kHz, 150 kHz, 200 kHz, and 500 kHz. As seen in Figure 3(a), when using a frequency of 50 kHz, the induced currents are concentrated at the root region with extremely little heat generated at the flank. Due to equation 10, as the frequency is minimized, the skin depth is maximized. Penetration is deepest in the direction of the heart of the spline. For a frequency of 100 kHz, the results are no different than for 50 kHz, with slight displacement of the induced currents toward the surface. See Figure 3(b). The temperature in the tip is a little higher than when f = 50 kHz. When using a frequency of 150 kHz, no additional heat is generated in the deeper root of the spline, and the induced currents migrated farther toward the tip
Figure 2. Temperature distributions (˚C) for different frequency. (a) 50 kHz; (b) 100 kHz; (c) 150 kHz; (d) 200 kHz; and (e) 500 kHz.
Figure 3. Evolution of temperature distribution (˚C) versus heating time for different frequency. (a) 50 kHz; (b) 100 kHz; (c) 150 kHz; (d) 200 kHz; and (e) 500 kHz.
of the spline. See Figure 3(c). For a frequency of 200 kHz, the induced currents are concentrated at the tooth tip and flank with some heat generated at the root. The skin depth is less than when MF is used. See Figure 3(d). When the frequency increases to 500 kHz (VHF), as shown in Figure 3(e), the skin depth becomes very small compared to that seen with HF and MF. The induced currents do not sufficiently penetrate the spline. The only region where the temperature reaches 1000˚C is the upper tip of the teeth. In conclusion, the frequency affects the temperature profile by changing the skin depth. When the frequency increases, the skin depth decreases. When the skin depth decreases, the temperature profile becomes narrower and is more restricted to the tooth tip.
High frequency induction heating has a shallow skin effect, which is more efficient for small parts, and low frequency induction heating has a deeper skin effect, which is more efficient for larger parts. As a rule, heating smaller parts requires higher operating frequencies (often greater than 50 kHz), and larger parts are more efficiently heated with lower operating frequencies. Temperatures at the tip and at the root are calculated for all frequencies and are shown in Table 1.
The effect of heating time over temperature distribution is the same at all five frequencies. The temperature increases when the heating time increases. At the beginning of the process, the heat is concentrated in a minor region and starts to spread as the time increases. In the case of MF, the heat started to spread outward from the root without touching the tip. In the case of HF, it started in the flank and spread without touching the root. Finally, in the case of VHF, it started from the tip and spread just through the tip of the tooth.
Predicted hardness depends of the frequency used in the simulation. As the hardness pattern is linearly linked to the temperature distribution, hardness can be analyzed in a fashion similar to the temperature profile in the previous part. For a frequency of 50 kHz, only the deep root is transformed to martensitic composition as illu-
strated in Figure 4(a). As the frequency increases, the hardened region migrates from the root toward the extreme tip of the spline tooth as demonstrated in Figures 4(b)-(e). This is due to the skin effect and equation 10.
It is important to analyze the effect of frequency on temperature at the end of the heating period (t = 1 s). After measuring the temperature at the tip and root for all frequencies (Table 1), it is seen that these two temperatures intersect at a frequency of 180 kHz as illustrated in Figure 5. This means that for a frequency of 180 kHz and for a specific







4. Prediction of the Hardened Profile and Validation
As seen in the previously, the frequency that gives the uniform temperature distribution is equal to 180 kHz. This frequency value is used to find the correct induced current density that meets the criteria leading to uniform temperature distribution. As illustrated clearly in Figure 6, when frequency is equal to 180 kHz, 

4.1. Prediction of the Hardened Profile
The AISI 4340 spline has a high core hardness, 





The four region limits are calculated in Figure 7(a) for the tip and Figure 7(b) for the root. In fact, it is sufficient to calculate the x-axis coordinates of the points at the intersections of the temperature versus depth curve and








Table 1. Temperature measurements in the tip and the root versus frequency.
Table 2.


Figure 4. Predicted hardened profile for different frequency. (a) 50 kHz; (b) 100 kHz; (c) 150 kHz; (d) 200 kHz; (e) 500 kHz.
Figure 5. Temperature versus frequency for the tip (blue) and the root (red).
Figure 6. Induced current density versus frequencies.

Figure 7. Temperature (˚C) versus depth for (a) the tip and (b) the root.
The horizontal hardness value of the first region demonstrates that it was transformed to a martensitic structure. The hardness drops dramatically in the second region. In this region, the material tries to affect a reaction opposing the action of heating, and the hardness reaches a minimal value. In the third region, the hardness value increases again to its initial value. This is normal, as it is closer to the core. The last region represents the material with unaffected microstructure. Both the tip and the root surfaces are hardened using a single frequency current. The spline is hardened in the surface and not in the core. The core hardness does not change. This is normal for surface treatment, which is meant to be the most concentrated on the surface as it is the region that is always in contact with other components. Since this is the region that will deteriorate the most quickly, hardness must be maximal on the surface and in the skin depth.
Data in Table 2 is used to representthe hardnessversus depth curve from the surface to the core. These curves are compared to the ones resulting from the micro measurements of the heated specimen. Graphs in Figure 8 show that the hardness is predicted with an excellent accuracy between d = 0 mm to d = ds. The measured hardness present uniform profiles along the maximum hardened region.
From 

The predicted model is very accurate in the tip of the spline tooth, as opposed to in the root where results are not very similar. In fact, the predicted hardness in the root is slightly delayed, in terms of depth, from the measured hardness. This is due to edge effects and experimental errors. In the simulation only one twelfth is studied due to symmetrical aspect of the model, but when the real spline was treated there were no edges because the spline was not divided.
4.2. Validation
Even with the small error in the root simulation due to edge effects, it is seen that the predicted and the measured hardened regions are quite similar. The machine parameters used in the simulation produced a good hardened pattern as compared to the real pattern achieved using the induction machine. The results obtained demonstrated that the hardened region depends directly on machine parameters. This region can be reduced by using high frequencies and decreasing heating time as depicted in Figure 9.
5. Conclusion
In this work, induction heating process is applied to a spline shaft in order to understand the effect of frequency and heating time on the final temperature distributions and hardness profile. The model used to evaluate the sur- face hardening attributes is based on coupled electromagnetic and thermal fields analysis. The achieved results

Figure 8. Predicted and measured hardness versus depth in (a) the teeth and (b) the root.

Figure 9. Predicted (a) and (b) measured hardness profiles.
establish that the proposed model can provide an accurate prediction of temperature distribution and precise
approximation of the hardness profile beside a comprehensive analysis of induction heating parameters effects, especially medium, high and very high frequency currents. The simulation results are validated by data from numerous and structured experiments. The results present a good agreement between simulation and experimental data. This work opens an interesting perspective to investigate the use of multi-frequency currents and various design involving multiple coils and scanning processes.
Cite this paper
Habib Hammi,Abderazzak El Ouafi,Noureddine Barka, (2016) Study of Frequency Effects on Hardness Profile of Spline Shaft Heat-Treated by Induction. Journal of Materials Science and Chemical Engineering,04,1-9. doi: 10.4236/msce.2016.43001
References
- 1. Semiatin, S.L. and Stutz, D.E. (1987) Induction Heat Treatment for Steel. 2nd Edition, American Society for Metal, Metals Park, Ohio.
- 2. Rudnev, V., Loveless, D., Cook, R. and Black, M. (2003) Handbook of Induction Heating. Marcell Dekker Inc., New York.
- 3. Hammi, H., Barka, N. and El Ouafi, A. (2015) Effects of Induction Heating Process Parameters on Hardness Profile of 4340 Steel Bearing Shoulder Using 2D Axisymmetric Model. International Journal of Engineering and Innovative Technology, 4, 41-48.
- 4. Barka, N., El Ouafi, A., Chebak, A., Bocher, P. and Brousseau, J. (2012) Sensitivity Study of Temperature Profile of 4340 Spur Gear Heated by Induction Process Using 3-D Simulation. Journal of Applied Mechanics and Materials, 232, 736-741.
http://dx.doi.org/10.4028/www.scientific.net/AMM.232.736 - 5. Chebak, A., Barka, N., Menou, A., Brousseau, J. and Ramdenee, D.S. (2011) Simulation and Validation of Spur Gear Heated by Induction Using 3D Multi-Physics Model. World Academy of Science, Engineering and Technology, 59, 893-897.
- 6. Zinn, S. and Semiatin, S.L. (1988) Elements of Induction Heating: Design, Control, and Applications. ASM International, Metals Park, Ohio.
- 7. Lin, C.Y., Wu, M., Bloom, J.A., Cox, I.J. and Miller, M. (2001) Rotation, Scale, and Translation Resilient Public Watermarking for Images. IEEE Transactions on Image Process, 10, 767-782.
http://dx.doi.org/10.1109/83.918569 - 8. Lienhard IV, J.H. and Lienhard V, J.H. (2008) A Heat Transfer Textbook. Phlogiston Press, Cambridge, Massachusetts.
- 9. Jungwirth, M. and Hofinger, D. (2007) Multiphysics Modelling of High-Frequency Inductive Device. The Proceeding of the COMSOL Users Conference, Grenoble, 2007.
- 10. Li, M.Y., Xu, H.B., Lee, S.-W.R., Jongmyung, K. and Daewon, K. (2008) Eddy Current Induced Heating for the Solder Reflow of Area Array Packages. IEEE Transactions on Advanced Packaging, 31, 399-403.
http://dx.doi.org/10.1109/TADVP.2008.923385 - 11. Barka, N., Chebak, A., El Ouafi, A., Bocher, P. and Brousseau, J. (2012) Study of Induction Heating Process Applied to Internal Gear Using 3D Simulation. Journal of Applied Mechanics and Materials, 232,736-741.
http://dx.doi.org/10.4028/www.scientific.net/AMM.232.736
NOTES
*Corresponding author.









