Journal of Materials Science and Chemical Engineering
Vol.03 No.11(2015), Article ID:61100,6 pages
10.4236/msce.2015.311001
Nano Structures and Its Thermodynamic Properties Using TIM
Ali Asghar Khakpoor1*, Bahare Agahi Keshe2, Ali Agahi Kesheh3
1Department of Physics, Islamic Azad University-Central Tehran Branch (IAUCTB), Tehran, Iran
2Departments of Mathematics, Islamic Azad University-Science and Research Branch (IAUSRB), Tehran, Iran
3Departments of Chemical Engineering, Islamic Azad University-North Tehran Branch (IAUNTB), Tehran, Iran

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2015; accepted 9 November 2015; published 13 November 2015
ABSTRACT
Manufacturing parts in nanoscale and investigating their properties has involved some limitations, and in some cases it is practically impossible; therefore, scholars have recently focused on micro-parts in natural scale, which has led to the advent of the field of nanostructures. Phenacenes with formula C4n+2H2n+4 are a family of organic molecules which have received a lot of attention in nanoscale. However, investigating the thermodynamic properties is highly expensive, especially when there are more than 6 loops. The present study was conducted in order to predict the thermodynamic properties of phenacenes family by using Topological Indices Method (TIM). Topological index is a numeral molecular graph which is referred to as molecular graph. This number indicates some molecular properties. One of the topological indices is RRR which is investigated and measured in phenacenes family. Afterwards, by calculating Heat of Formation and Gibbs Energy for some members of this family and comparing them with data provided by valid articles, we could propose an appropriate model to predict some thermodynamic properties of this family.
Keywords:
Nanostructures, Gibbs Energy, Heat of Formation, Acenes, Nanostructures, ISI Index

1. Introduction
Nowadays, scientists try to design and provide nanometer parts. Restricted parts manufacturing at the nanoscale made it practically impossible in many cases. Therefore, scientists’ interest to make smithereens in the natural scale, has led to creation of nanostructures field in recent years [1] [2] .
Aromatic loops are known as the family of organic compounds structure with double bond in the loop. Aromatics constitute a wide range of compounds including benzene and its derivatives. Aromatics participate in a substitution reaction that is one of the indicator traits of this category.
Aromatic hydrocarbons include an unsaturated benzene loop that is very stable, and often act like a saturated compound.
Acenes are a category of aromatics family which is highly regarded in recent years due to their nanostructures dimension [3] [4] . However, examination of physical, chemical, optical, electrical and thermodynamic properties of heavier Acenes is difficult in many cases and requires a high expenditure as well as it is impossible in some cases. Therefore, existence of an appropriate model for predicting the properties finds a special importance. One of the cheap and effective methods is Topological Indices Method (TIM) [5] - [10] .
Topological indices are real numbers introduced during the studies on molecular graphs in chemistry, and are constant about isomorphism of the graphs. These indices can suggest some molecular properties. They were introduced in 1947 by Professor Wiener for the first time, and were started with Wiener index introduction to predict the chemical properties of naphthalene [11] .
Topological indices are defined based on graphs parameters such as vertices degree, the distance between the vertices, etc. It can be described and predicted some chemical, physical, electronic properties of molecules by using these indices. Topological indices are divided into different categories according to their definition. In this study the ISI index (Inverse Sum Index) was used, which was introduced in 2010 by Damir Vukičević and Marija Gašperov. It is defined based on the vertices degree [12] .
Definitions
In mathematical, a non-empty set of objects identified as vertices (V) is called a graph. This vertices are connected by lines called edge (E), and are showed as G = G (V, E). A molecular graph is a simple graph whose vertices are composed from the atoms of a molecule, and bonds between atoms of the molecule make up edges of the graph. In chemical graphs hydrogen atoms are removed, and they are discarded. Dehydrogenized graph is said to these graphs in phrase. As well as all bonds between the atoms are considered as unique, and the degree of each vertex will be 4 maximally [13] [14] . One of the topological indices is ISI index which is defined as Equation 1 [12] :
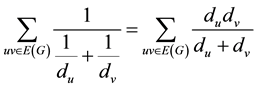 (1)
(1)
where du and dv are degrees of u and v vertices, respectively, and they have a common bond together.
2. Theory and Methods
In this paper by expression and proof of the theorem, we initially examined ISI (G) topological index given in Equation (1) in the family of linear Acenes, and we will try to prove an equation for each index based on the loops number (n). Then, we will obtain the amounts of this index in some family members of linear Acenes. We will also obtain amounts of Gibbs Energy and Heat of Formation (T = 298.15 K, p = 1 atm) for selected members of the family by applying Chemoffice 2015 software. Finally, we try to present an appropriate model for determining the amounts of Gibbs Energy and Heat information on this family, especially for the members with a large number of loops.
Consider simple molecular graph of linear Acenes family (C4n+2H2n+4) is shown in Figure 1.
Theorem:
Suppose n is the number of loops in the linear Acenes family, then the ISI (G) index is equal to:
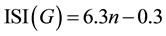 (2)
(2)
Proof:
Figure 1 shows the simple graph of Acenes family that can be divided into three areas:
1) All vertices and edges that are located on and top of L = 1 level, which is called G1 (Figure 2).
2) All vertices and edges that are located on and lower L = 2 level , which is called G2 (Figure 3).
3) All vertices and edges that are located between L = 1 and L = 2 levels, which is called G3 (Figure 4).
Figure 1. Figure shows the simple molecular graph of linear Acenes family.
Figure 2. G1 is all vertices and edges in the graph of Figure 1 that are located on and top of L = 1.
Figure 3. G2 is all vertices and edges in the graph of Figure 1 that are located on and lower the L = 2.
Figure 4. G3 is all vertices and edges in the graph of Figure 1 that are located between L = 1 and L = 2.
Regarding to Figure 1 and Equation (1), for G1 we have:
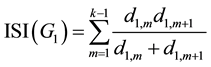 (3)
(3)
For the first and last two sentences in Equation (3) related to vertices X1,1 and X1,k, we have:
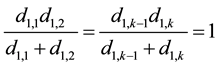 (4)
(4)
And for m ≠ 1 and m ≠ k − 1, we also have:
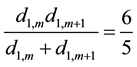 (5)
(5)
Thus, Equation (3) becomes as follows according to Equations (4) and (5):
 (6)
(6)
Given to k = 2n + 1, since we have:
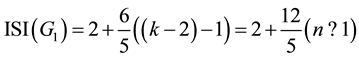 (7)
(7)
For the G2 area as shown in Figure 3 we also take a similar result:
 (8)
(8)
But for G3 area, since it only includes X1,m: with odd m, according to Figure 4 we have:
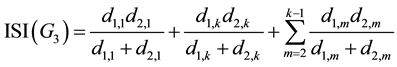 (9)
(9)
Here, we also separate the first and last sentence, and for these two sentences we have:
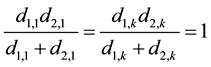 (10)
(10)
as well as other sentences collected in the Equation (9) are equal:
 (11)
(11)
According to Equations (11) and (10), Equation (9) comes as follows:

Since

and by applying Equations (7), (8) and (12) we reached Equation (2), and the Theorem is proven.
3. Results
By applying Equation (2), ISI index for the first eight elements of the family were calculated and presented in Table 1.
We calculated Gibbs Energy (T = 298.15 K, p = 1 atm) and Heat of Formation (T = 298.15 K, p = 1 atm) in the Acenes family (C4n+2H2n+4) using empirical data to investigate the thermodynamic properties, and we compared it with authoritative sources. The results are shown in Table 2.
In Figure 5 changes diagram of Gibbs Energy (G.E) in the linear Acenes family (C4n+2H2n+4) is drawn based on ISI index. This diagram shows the success of ISI index in prediction of Gibbs Energy is the linear Acenes family. This precision is accompanied with R2 = 1 and is shown in Equation (14).

Also, in Figure 6 Heat of Formation (H. o F.) in the Acenes family is plotted based on ISI index. Figure 6 shows high precision of ISI index in predicting Heat of Formation (H. o F.) of Acenes linear Family with R2 = 1.
Table 1. ISI index in the Acenes family.
Table 2. Gibbs Energy and Heat of Formation (at T = 298.15 K, p = 1 atm).
Figure 5. Gibbs Energy (G.E) in linear Acenes family based on ISI index.
Figure 6. Heat of Formation (H. o F.) in the linear Acenes family based on ISI index.
This situation is possible with Equation (15).

4. Conclusion
Prediction of some thermodynamic properties of nanostructure materials is possible by applying TIM. This issue is particularly important when using experimental methods leads to waste of time and financial expenditures in large amounts and theoretical methods have not been successful. We are facing with this situation in the linear Acenes family, and whatever number of loops increases, the situation will be more difficult, more complex and more expensive. Here, we can predict Gibbs Energy and Heat of formation in the Acenes family (at T = 298.15 K, p = 1 atm) by applying the TIM and Equations (14) and (15). We have done this prediction for eight heavier members of the linear Acenes family by applying TIM. The results are shown in Table 3.
Table 3. Prediction Gibbs Energy and Heat of Formation in the Acenes family (at T = 298.15 K, p = 1 atm).
Acknowledgements
We would like to thank Islamic Azad University-Central Tehran Branch (IAUCTB) for helpful protections. Also we acknowledge all those who have helped us with their support and cooperation in conducting this study.
Cite this paper
Ali Asghar Khakpoor,Bahare Agahi Keshe,Ali Agahi Kesheh, (2015) Nano Structures and Its Thermodynamic Properties Using TIM. Journal of Materials Science and Chemical Engineering,03,1-6. doi: 10.4236/msce.2015.311001
References
- 1. Wang, Z.L. (2004) Zinc Oxide Nanostructures: Growth, Properties and Applications. Journal of Physics: Condensed Matter, 16, R829-R858.
http://dx.doi.org/10.1088/0953-8984/16/25/R01 - 2. Baladié, I. and Buzdin, A. (2003) Thermodynamic Properties of Ferromagnet/Superconductor/Ferromagnet Nanostructures. Physical Review B, 67, Article ID: 014523.
http://dx.doi.org/10.1103/PhysRevB.67.014523 - 3. Waser, R. (2012) Nanoelectronics and Information Technology. 3rd Edition, WILEY-VCH.
- 4. Patolsky, F., Timko, B.P., Zheng, G. and Lieber, C.M. (2007) Nanowire-Based Nanoelectronic Devices in the Life Sciences. MRS Bulletin, Cambridge University Press, Cambridge.
- 5. Khakpoor, A.A. (2015) Prediction Electronic and Physical Properties of Nano Structures; Topological Index Method. International Journal of Advanced Research, 3, 1536-1540.
- 6. Khakpoor, A.A. and Agahi Keshe, B. (2015) Electronic and Optical Properties of Nanostructures and Its Relationship with Harari Index. Journal of Materials Science and Chemical Engineering, 3, 8.
http://dx.doi.org/10.4236/msce.2015.38001 - 7. Khakpoor, A.A. and Agahi Keshe, B. (2015) Some Electronic and Optical Properties of Nanostructures Using the First Zagreb Index. International Journal of Advanced Research, 3, 548-551.
- 8. Khakpoor, A.A. and Agahi Keshe, B. (2015) Determination of Physical-Chemical Properties of Titanium Organic Compounds Using Topological Indices; QSPR techniques. International Journal of Current Research, 7, 15686.
- 9. Khakpoor, A.A. and Agahi Keshe, B. (2015) The Relation between Total π Electron Energy of Linear Acenes as Nanostructures and Topological Indices. Journal of Computational and Theoretical Nanoscience, Accepted for Published.
- 10. Khakpoor, A.A. and Agahi Keshe, B. (2015) Physical and Electro-Optical Properties of Rylenes as Nanostructures Using Topological Indices Method. Journal of Nanoelectronics and Optoelectronics, Accepted for Published.
- 11. Wiener, H. (1947) Structural Determination of Paraffin Boiling Points. Journal of the American chemical Society, 69, 17-20.
http://dx.doi.org/10.1021/ja01193a005 - 12. Vukicevic, D. and Gasperov, M. (2010) Bond Additive Modeling 1. Adriatic Indices. Croat. Chem. Acta., 83, 3, 243- 260.
- 13. Trinajstic, N. (1992) Chemical Graph Theory. 2nd Edition, CRC Press, Boca Raton.
- 14. Ezra, G.S. (1982) Lecture Notes in Chemistry. Springer, Germany.
NOTES
*Corresponding author.









