Received 2 March 2015; accepted 25 March 2015; published 27 March 2015

ABSTRACT

In this work, the mechanism of interaction of pittings, occurring on the heterogeneous surface of the passivated metal at presence in an aqueous electrolyte solution the activating (halide) anions is developed. A mathematical scheme describing this mechanism is presented. The equations for the currents density of the anodic dissolution of pitting as a function of concentration of activating anions and free water are obtained. The closed system of the equations representing a basis theory of an interaction of pittings is obtained.

Keywords:

Pitting, Electrolyte, Depassivation, Metal, Dissolution

1. Introduction

Pittings are called, as is known, local, i.e., small on the area (with a radius of r ~ 10^-2 to 0.5 cm), but deeply penetrating, often through the destruction of the metal lattice in the electrolytes, occurring on the mechanism of its anodic dissolution.

Pittings spontaneously appear as a result of the interaction of the metal surface with an electrolyte with the values of the anode potential, which corresponds to the region of the passiveness of metal and the presence in electrolyte a sufficiently high concentration of activating anions. The most dangerous of them are 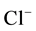ions.

The internal surface of a pitting is dissolved at a rate by (10² to 10⁴) times greater than the rate of dissolution of the surrounding metal surface.

Therefore at the small on mass loss of metal, pittings render inoperable large metal structures, limiting the periods of their exploitation service in different production technologies and other regions.

Consequently, there are many experimental studies concerning pittings but the pitting process theory is underdeveloped. It is necessary to highlight the problem of the localization mechanism of pitting, the mechanism of their interaction and the mechanism of their growth. These tasks can be considered independently.

In [1] [2] , the problem of the growth of a single pitting is examined. In fact, on the metal surface 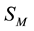there arise many [3] pittings, only a few of which survive and develop due to their interactions, for the first time considered in the article.

Relative to this interaction in [1] [2] is expressed only the idea about the fact that, for survival and increase of an emerged pitting ( the development of its nucleus, i.e. a locally depassivated section 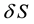of the surface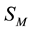) is necessary the particular volume 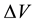of the electrolyte solution, from which the developing pitting is capable to obtain the necessary for its increase reagents, precisely, the water molecules and the activating anions, for example halide. For them, the boundary of the region 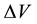may not coincide and in process of development of pitting to be displaced. Interaction considerably of pittings is reduced to competitive fight for volume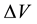. This idea is developed below, taking into account the results of [1] [2] , for example system Fe in the aqueous solution HCl used in [4] in the case of chrome.

2. Laws of Interaction of Two Pittings

According to [5] , the density 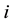current in the model of pitting reaches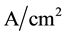. The related utilisation of the aqueous solvent for the hydration of metal ions 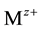leads to dehydration of the electrolyte near the bottom of pitting. In [1] [2] it is shown that in the layer with a thickness of 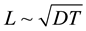equal to the depth of the diffusional penetration for a characteristic time 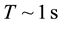[5] the development of the pitting of concentration 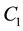of metal

ions 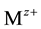reaches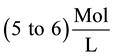. The solution of such a concentration simulating pitting is obtained, for ex-

ample in [6] [7] . Therefore, when the value of the hydration number is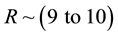, a significant portion of water molecules is included in the hydration shell and current of hydrated ions of metal are assigned to the periphery. Consequently, the aqueous solvent is not a fixed medium, in which the ionic impurities of smaller concentrations diffuse. It is divided into free and that connected with the oppositely directed flows. In this sense, an electrolyte is dehydrated, and the ratio between the actual rate of the electrochemical reaction and the supply of free water becomes relevant.

Under these conditions, it is known [8] [9] , the Fick’s law discontinues to work in the transfer equations commonly used in electrochemistry. The concentration and density of the flow of the free water is comparable in size with the concentrations, and the densities of the flows, of the hydrated metal ions and anions. Therefore, dehydration can only be described by Onsager equations [8] [9]

(1)

where―the electrochemical potential of i-th component,―the average velocity of the particles of i-th component,―convection velocity. In [8] , these equations are written in the other variables. If the concentrations of the ion components become smaller, then after the relevant series expansion in the linear approximation from (1) the usual Fick’s laws used in electrochemistry are prepared. The general solution of Equations (1) is obtained in [1] [2] and is not provided here.

The above assessment of the concentration of metal ions refers to a single pitting. But in reality they occur at many quite active (at a given concentration of the activating anions) sections of the metal surface, their density reaches the value of [3] . If for some value the potential of pitting creation corresponds to the section with the activity (characterising the current density of dissolution), then pittings that can be conceived in all sections with.

Therefore, the volume of electrolyte solution is divided into areas, each of which belongs to only one of the pittings obtaining from it reagents necessary for its development, i.e. a free solvent and activating anions. Their flows directed to the bottom in the case of each pitting are localised in the field belonging to it. By this are determined its boundaries, which can displace as long as pitting is developed and which do not cross the water flow lines.

In [1] [2] the areas are called the “living space” of pittings, and have not been studied so far. The strong (i.e. generating greater current) pittings require a higher number of reagents, which increases as long as they develop. At some stage, the growth rate determined by the current level begins to exceed the rate of supply of reagents and also at a high density of pittings there is a deficiency of the reagents. Accordingly, the interaction begins, i.e. competition for the living space, in which strong pittings suppress their competitors.

At first let us consider the mechanism of this process by the example of a model of two coupled pittings, Figure 1. it is simplified geometrical part of the problem while maintaining all physical factors and obtained is a closed self-consistent system of relations describing the mechanism of interaction.

In this model, two interacting pittings are modelled by the anodic dissolving surfaces and with an area of the required value, i.e. the frontal boundaries of the horizontal cylinder (or parallelepiped) with the length of the electrolyte filled with a solution. It consists of the adjacent areas and owned by pittings and (i.e. their “living spaces”). The potential of these surfaces corresponds to the pitting creation area. The cathode in this model in the form of a metal lattice (or ring) sufficiently transparent for the free water flows can be placed in a section normal to the cylindrical axis between the anodes, and position it at different distances between and. Such a structure generalises the model [5] of the artificial pitting in which the value of reaches. The current densities and of the surface dissolution and are not the same. The cathode reaction can be [4] :

As outlined above, by dissolving the water flows arise and, where R―the number of hydration of

ions which compound currents and. Due to the difference of the flows the volumes and change and the plane surface, which delimits them, shifts, i.e.

On it are continuous the values of free water concentrations in volumes and which should be maximum in the plane of the division. Due to the high pitting current dissolution density, the electrolyte mass density increases in its environment. Therefore there is a flow of convection. The conditions for conjugation of concentrations and flows at the boundaries between regions are obtained. The equations of the model with the flows (1) and the condition of electrical neutrality in the area of a strong (at) pitting taking into account the allocation at the cathode hydrogen of the following:

(2)

where―the molar mass of the ions, counter-ions (т.е), free water and hydrogen with the concentration. In the area of the weak pitting the right sides of Equation (2) (describing volume sources) are equal to zero. The boundary conditions on the surfaces and

(3)

Similar conditions for convection flows

(4)

According to the mathematical physics [10] in the Equation (2) the value of q on the right means the function of the hydrogen flow caused by its participation in the cathode reaction. According to its meaning q is equal to the amount of hydrogen utilised in on the unit cathode surface (i.e. number of moles/cm²・sec). For each mole of metal ions on the cathode utilised is moles of hydrogen. The value―the specific cathode surface with the dimension of the inverse length. The outflow intensity is determined by the condition of equality of currents and the cathode reaction currents corresponding to them. By using it and [10] we get

where x_k―cathode plane coordinate,―cutting δ-function [10] . The plane motion equation , dividing the areas and

(5)

If, then the right side (5) is positive, i.e. the interface is displaced toward the weak pitting, and its “living space” is reduced. The conjugation conditions on this plane of concentrations and convections have the form

(6)

where the upper signs (+) and (−) mean the opposite sides of the interface. The Equations (1)-(6) are integrated separately in the areas and, i.e. in limits

They are considered in the coordinate system, connected with metal electrodes. The initial conditions for them determine the composition of the electrolyte, that allows to study its influence on the pitting formation. In (1)-(6) current density of anodic dissolution of pitting can be related to the concentration and activating anions and free water. For that purpose, it is sufficient to use the results of the works [11] - [14] that are based on the extensive experimental data and having fundamental value. According to [11] - [14] , the activating anions and water molecules are directly involved in elementary acts of anodic dissolution by lowering the energy barrier of transition of metal ions in the electrolyte. Chemisorbed on the metal surface they form with its ions the intermediate short-lived complexes, weakly connected with the lattice. In the general case, the act of dissolution consists, therefore, of the stages of the chemical adsorption of the molecules of water and activating anions, their subsequent ionization with transition to electrolyte and dissociation, as a result by which anions regenerate. In [15] - [18] this approach is specified. Accordingly, in the case of pitting the kinetic scheme of dissolution of its bottom takes the form

(7)

where the stoichiometric number is less than the hydration number. This scheme is supported at least by the fact that in low concentration of chlorine ions pittings do not occur, and the deficit of free water according to [5] decreases the rate of dissolution and changes its kinetics. In [1] [2] the scheme (7) is detailed and the currents are determined in the form as follows

(8)

where the index means, as before, the value’s belonging to the surface of the bottom of a pitting. The formula (8) closes the system of Equations (1)-(6) providing the basis for the theory of interaction of pittings.

3. Conclusion

In conclusion, we should note that apparently only with the model on Figure 1, the dehydration effects, which stop weak pitting growing, can be identified and explicitly observed. In the case of the more complicated actual geometry, an arrangement of interacting pittings in the same anodic horizontal plane of the interface areas is no longer flat. Consequently, the Equation (5) will change, on the right side of which there should be only normal to the interface components of the vectors determining the ionic and convective flows. The accounting of the specified complication of geometry (and also the analysis of possibility of other mechanisms of interaction and their concrete calculations) is a subject of new works.

References