Journal of Materials Science and Chemical Engineering
Vol.2 No.9(2014), Article ID:49536,11 pages
DOI:10.4236/msce.2014.29001
Scale-Up of the Polyol Process for Nanomaterial Synthesis
Samir Farhat1*, Nassima Ouar1, Mongia Hosni1, Ivaylo Hinkov2, Silvana Mercone1, Frédéric Schoenstein1, Noureddine Jouini1
1Laboratoire des Sciences des Procédés et des Matériaux, CNRS, LSPM-UPR 3407, Université Paris 13, PRES Sorbonne-Paris-Cité, 99 Avenue J.-B. Clément, 93430 Villetaneuse, France
2Département de Génie Chimique Université de Technologie Chimique et de Métallurgique, 8 Boulevard St. Kliment Ohridski, 1756 Sofia, Bulgarie
Email: *samir.farhat@lspm.cnrs.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2014; revised 17 July 2014; accepted 13 August 2014
Abstract
Two classes of inorganic materials such as metallic nanowires and metal oxides nanorods were synthesized using the polyol process and scaled-up to produce macroscopic quantities. Scale-up strategy was successfully built by performing the synthesis in a 15 cm diameter, 4.5 liters volume cylindrical tank using a straight paddle impeller and a Rushton turbine. The actual yield of the synthesis is ~45 grams per batch for zinc oxide nanorods and ~20 grams per batch for cobalt nickel nanowires. Under the same rotation speed, the aspect ratio of the produced nanowires and nanorods using the Rushton turbine impeller with radial flow patterns has shown a lower aspect ratio, nanoparticle size and polydispersity. This is attributed to the increase of the local dissipated energy as spatially calculated by computational fluid dynamics (CFD) that is proposed to design, optimize and scale-up the polyol process.
Keywords: CFD Simulation, Polyol Process, Nanomaterial Synthesis

1. Introduction
For nanomaterial synthesis, polyol-mediated process is nowadays considered as a very interesting alternative to sol-gel route. While sol-gel route leads to oxides or hydroxides, the polyol-mediated synthesis enables to prepare more classes of inorganic materials (metal, hydroxides, oxides…). It has been established that two main reactions occurred in these media: reduction and hydrolysis, the first leading to metals [1] and the second to hydroxides or oxides [2] . Synthesis of such nanomaterials has gained increasing interest during these two last decades due to technological applications such as information storage [3] or photovoltaic devices [4] . While the majority of these applications rely on precise growth of uniformly sized and shaped nanoparticles, controlled and reproducible synthesis in large scale remains a major challenge which can be addressed through a deeper understanding of nucleation, growth and agglomeration/breakage kinetics connected with heat, mass and momentum transfers in the reaction vessel. As these rate processes are scale dependent, one important task is to find a reliable way to design or model larger scale processes using information obtained from a smaller one. Unfortunately, publications concerning the scale-up of nanomaterials are very sparse in the literature, although its importance has been emphasized by their potential use as advanced materials in the industry. In contrast, classical precipitation from liquid phase in agitated vessels is more used in the chemical industry. Nevertheless, successful scaleup remains difficult due to the absence of a validated methodology that bridges the gap between molecular and macroscopic length scales over a wide range of time scales. Indeed, total similarity on these different scales cannot be fulfilled, as it is difficult or even impossible to maintain constancy in all the dimensionless groups that characterize geometry, thermal and mass transfers, kinetics of the nanoparticle synthesis process. This implies in the particular nanoparticles synthesis conditions that none of the conventional scale-up criteria as equal power input per unit mass, equal tip speed or equal stirring rate is capable of predicting the experimentally observed effects of the mixing conditions on particles size and polydispersity. For simplicity, similarity on different scales could be obtained when the dimensionless groups as Reynolds, Nusselt or Damköhler numbers have the same value on different scales. However, this is difficult to achieve for all the dimensionless groups that characterize the process. In these cases, a trade-off between different dimensionless groups has to be found to maintain geometric, thermal or chemical similarities with scale-up through weighting parameters according to their expected influence on the process. Scale-up then loses its theoretical base and becomes empirical [5] . An alternative approach consists of the mathematical modeling of the underlying physical and chemical processes in the reaction vessel with clearly and quantitatively understood mechanisms, which is not always the case. For these reasons, we built our strategy for scale-up batch precipitation in two steps. In the first step, the synthesis conditions were extrapolated empirically from the laboratory to the pilot scale and validated through ex situ characterizations of the obtained nanomaterials using X-ray diffraction (XRD), high transmission electron microscopy (HTEM), field emission gun scanning electron microscope (FEGSEM), and VSM-SQUID for the magnetic properties. In the second step, and since solving combined computational fluid dynamics (CFD) and population balance (PB) equations still impracticable due to the excessive computational demand and simulation time required [6] [7] , we performed CFD calculations to characterize the turbulent flow patterns and energy dissipation under different axial and radial impellers geometries. The results obtained by these scale-up approaches will be illustrated in this paper on two opposite materials: zinc oxide nanoparticles which is a semi-conducting material used for solar energy conversion based on the photovoltaic effect and metallic cobalt-nickel binary alloy nanowires with potential application in the fields of ultra-high density magnetic storage.
2. Empirical Scale-Up Approach
Zinc oxide and Co80Ni20 nanoparticles were prepared by extrapolating the stoichiometric conditions from the laboratory to the pilot scale with the intention to maintain the same particle size and morphology. Either axial or radial mixing was tested by using straight paddle and Rushton turbine respectively under the same chemical stoichiometry and the stirring speed. After synthesis, the obtained colloidal suspension containing the residual polyol and the nanoparticles were centrifuged, filtered and cleaned several times and the solid powder dried and characterized by JEOL 2011 transmission electron microscope (TEM) operating at 200 kV. To further confirm phase and morphology, X-ray diffraction was taken in 2q angle between 30˚ and 80˚. The XRD analysis was performed using 2INELTM diffractometers with Cu-Kα1 radiation for ZnO and Co-Kα radiation for Cobaltnickel.
2.1. Reactor Description
We designed a new pilot scale reactor that consists of a jacketed glass vessel 4.5 L in volume and 150 mm in internal diameter with double jacket and paddle stirrer. The same reactor was used to produce either zinc oxide or magnetic metals by simply changing the operating conditions. During the synthesis, external reactor surface was insulated from the ambient making the reactor nearly adiabatic. Compared to small lab-scale system, this configuration was designed to improve heat exchange in the reactor, minimizing heat losses since the surface area to volume ratio decreases with volume. In addition, due to the magnetic activity of the cobalt/nickel powder, the steel stirrer was fully encapsulated in Teflon® PTFE. The stirrer paddle was powered by a 50 Watt motor Heidolph RZR 2021 with a digital display and a speed range of 40 to 2000 rpm. As shown in Figure 1, thermal oil circulated through the reactor jacket from a Julabo PrestoLH40 cryo thermostat unit. Internal rector temperature was measured using a Pt100 thermometer with an accuracy of 0.1˚C. This parameter was controlled using a self-optimizing controller (ICC—Intelligent Cascade Control) operating in a wide working range from −45˚C to 250˚C. This allows a rapid heating and cooling and permit temperature stability.
2.2. Zinc Oxide Synthesis
Zinc oxide was obtained by forced hydrolysis of zinc acetate salts in diethylene
glycol as solvent [8]
[9]
. The chemicals used were zinc acetate dihydrate [(Zn(OAc)2∙2H2O)], and diethylene glycol
DEG [O(CH2CH2OH)2]
from Sigma-Aldrich. Distilled water was added to adjust hydrolysis ratio and ethanol
and acetone were used for washing and cleaning nanoparticles. All chemical were
of analytical grade without any further purification. To control reaction stoichiometry,
we defined the metal concentration in the polyol solution as z = [Zn2+] mol∙L−1
and the hydrolysis ratio as
 where
where
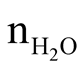 is the number of moles of water including those of zinc acetate dihydrate and
is the number of moles of water including those of zinc acetate dihydrate and
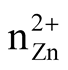 accounts for the number of moles of zinc precursor. The reaction was conducted with
h = 5, z = 0.5 at a controlled temperature of 170˚C during ~1 hour under continuous
stirring at 220 rpm. At these conditions, the solubility of the produced zinc oxide
in DEG is very low and high supersaturation is generated which leads to nucleation
and crystal growth visible when the solution color’s shift from transparent to the
white as shown on the photography of Figure 1(b).
After synthesis the white precipitate is washed and drayed.
accounts for the number of moles of zinc precursor. The reaction was conducted with
h = 5, z = 0.5 at a controlled temperature of 170˚C during ~1 hour under continuous
stirring at 220 rpm. At these conditions, the solubility of the produced zinc oxide
in DEG is very low and high supersaturation is generated which leads to nucleation
and crystal growth visible when the solution color’s shift from transparent to the
white as shown on the photography of Figure 1(b).
After synthesis the white precipitate is washed and drayed.
2.3. Cobalt-Nickel Synthesis
For cobalt/nickel nanowires, we used a metal reduction of cobalt and nickel salts introduced into the molar proportions of 80% cobalt and 20% of nickel as discussed in previous works [10] -[15] . Nanowires were obtained by reduction of Cobalt (II) Acetate Tetrahydrate 98% Co(C2H3O2)2∙4H2O and Nickel (II) Acetate Tetrahydrate 98%+ Co(C2H3O2)2∙4H2O in the presence of Ruthenium (III) Chloride hydrate 99.9% (PGM basis), Ru 38% min (RuCl3∙H2O) acting as nucleating agent. The polyol was the 1,2-butanediol (C4H10O2) and the base was sodium hydroxide (NaOH). All the chemicals were purchased from Sigma Aldrich. It was found that the basicity of the medium control the morphology of the nanowire [6] . The total concentration of cobalt-nickel in the polyol was 0.08 M, that of sodium hydroxide 0.15 M, and the relative concentration of the nucleating agent [Ru]/[CoNi] = 2.5 × 10−2. For such heterogeneous nucleation process, the number of the formed nuclei and their growth are controlled by [Ru]/[CoNi] ratio. As a consequence, this ratio governs the relative nucleation and growth rates thereby controlling the final nanowire size distribution.
 (a)
(a)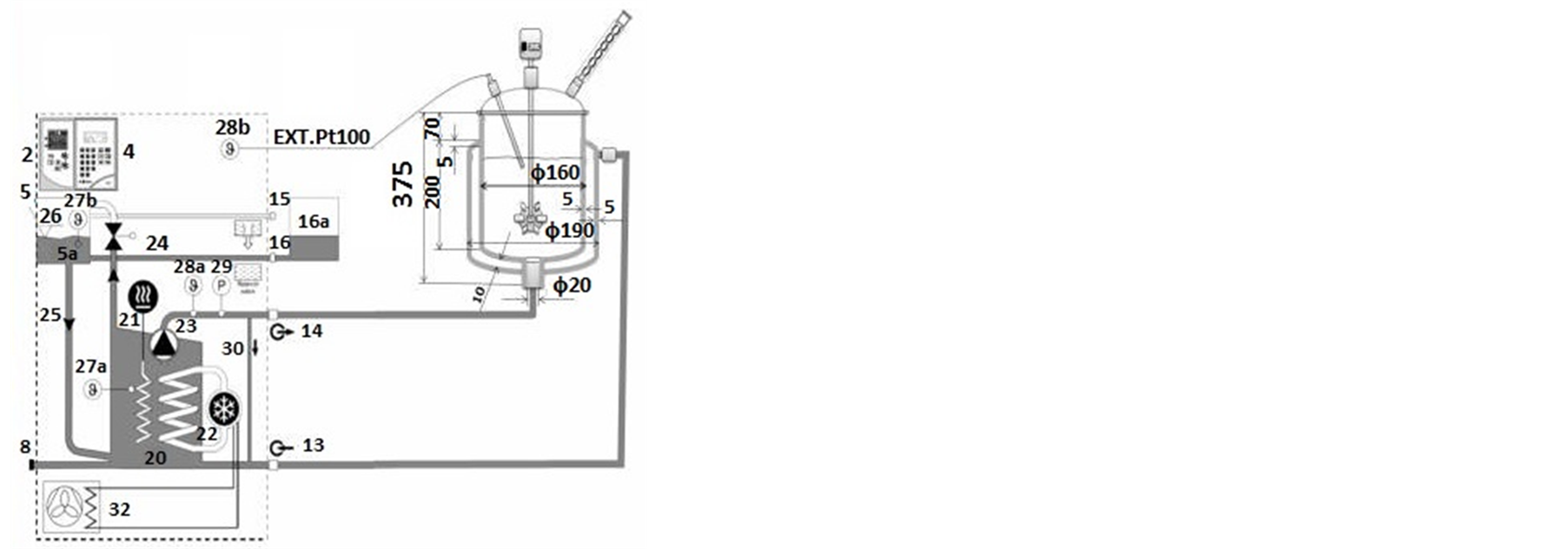 (b)
(b)
Figure 1. (a) Schematic of the pilot scale reactor with the overall recirculation heater circuit (grey) and photography of the pilot scale reactor under (b) ZnO and (c) Cobalt Nickel synthesis.
3. Results
In Figure 2, we report TEM pictures of the zinc oxide nanoparticles obtained under the same stoichiometry with straight paddle (S1) and Rushton turbine (S2) and their corresponding XRD measurements. The total yield of zinc oxide nanoparticles was not affected by the mixing configuration and is ~45 grams of dry material per batch. For small scale reactor the yield is ~1.5 g per batch. TEM pictures confirm the results obtained in small scale where similar ZnO rod-like morphology was obtained. A slight decrease in the nanorod aspect ratio between straight Paddle and Rushton turbine was observed as evidently depicted by the micrographs of Figure 2. The morphological parameters listed in Table 1 were determined from TEM pictures using the ImageJ software program and statistical analysis [16] . XRD patterns of samples S1 and S2 are also shown in Figure 2. They are in agreement with the standard X-ray diffraction peaks, which confirmed that the synthesized materials are wellcrystallized in both mixing situation. In addition, structural analysis confirms our previous results obtained in small scale reactor [16] [17] .
In Figure 3, are shown TEM pictures of the cobalt/nickel nanowires obtained with using straight paddle and Rushton turbine and their corresponding XRD measurements. The total yield of cobalt nickel nanowire was also not affected by the mixing configuration and is ~20 grams of dry material per batch. This yield is lower than zinc oxide synthesis due to different nucleation mechanism and supersaturation conditions. For comparison, the yield obtained at small scale synthesis was less than 1 g per batch. In contrast, a decrease in the nanowire aspect ratio between straight Paddle and Rushton turbine was observed from the statistical analysis of the micrographs of Figure 3. The morphological parameters are summarized in Table1 The X-ray diffraction patterns are showed in Figure 3 where the peaks appear particularly widened suggesting the formation of nano crystalline phases. More specifically, the peak (002) is a signature of a shape anisotropy objects with growth along the crystallographic c axis of the cobalt hcp phase. X-ray diffraction results obtained in pilot scales confirm the structure of the nanowires issued from small scale synthesis and already published [18] [19] .
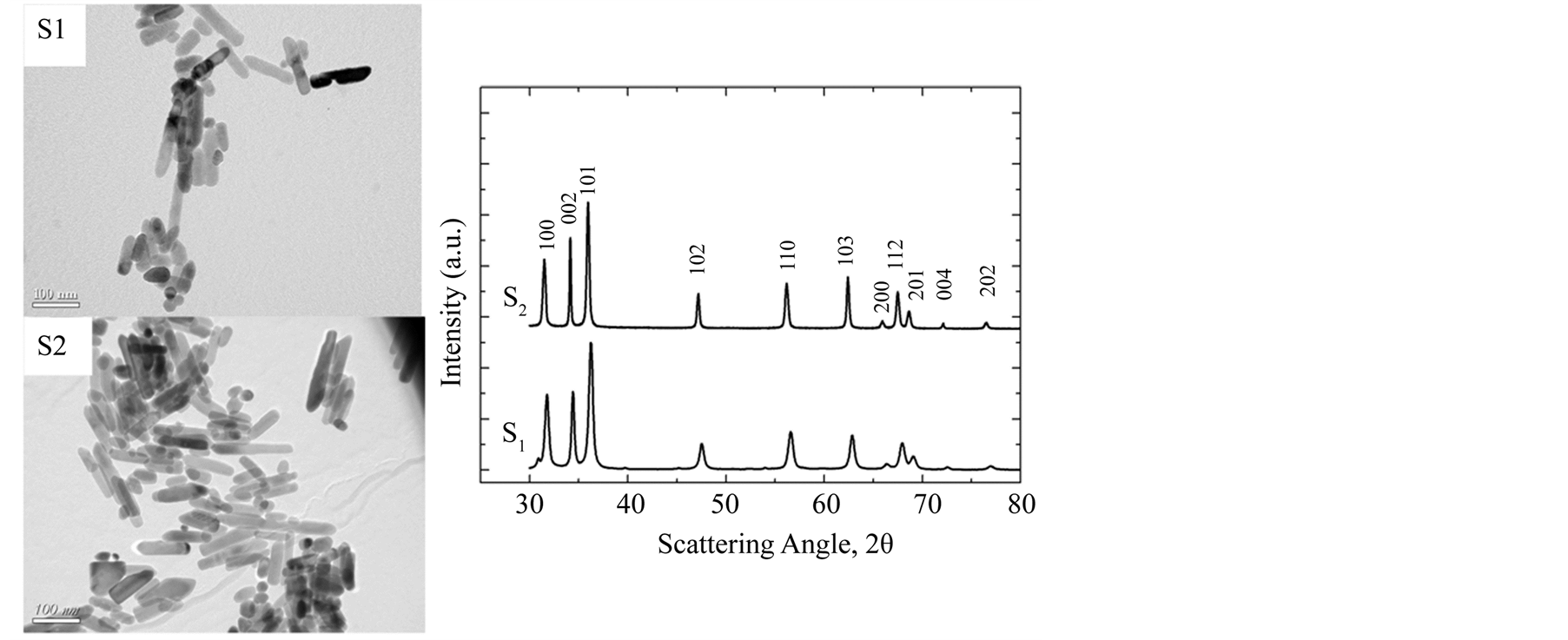
Figure 2. TEM pictures of ZnO nanoparticles obtained with straight paddle (S1) and Rushton turbine (S2) and their respective XRD patterns.
Table 1. Effect of mixing on nanoparticle size obtained in pilot scale. Here L is the nanowire or nanorod length (nm), d the diameter (nm) and L/d the aspect ratio.

Figure 3. TEM pictures of Co80Ni20 nanowires obtained with straight paddle (S3) and Rushton turbine (S4) and their respective XRD patterns.
Since the aspect ratio is crucial for magnetic properties, we compared the magnetic performances of the Co80Ni20 samples (S3) and (S4). Hysteresis loops were recorded by vibrating sample magnetometer VSM at room temperature and reported in Figure 4. From these results, we can conclude that the samples show a ferromagnetic behavior characterized by an open cycle, a saturation magnetization (Ms), a remanent magnetization (Mr) and a coercivity (Hc) suggesting that the scale-up is succeeded. Nevertheless, we can notice that the geometry of the paddle has also an effect on the coercive field Hc. When straight paddle was used, the measured coercive field was Hc = 2065 Oe (S3). In contrast, when Rushton turbine (E3) was used, the coercive field was significantly increased to Hc = 3922 Oe. Since the chemical stoichiometry of the reaction was the same, this abnormally elevated coercive field is attributed to the mixing efficiency.
Hence, in order to study the interaction between the bulk liquid phase flow and the tank and paddle geometries, we developed a CFD modeling for the four cases discussed above.
4. CFD Modelling
CFD calculations were performed in 3D turbulent fluid flow configuration for different type of agitators and solved using ANSYS FLUENT commercial software [20] . This allows the evaluation of an alternative design and the optimum mixing configuration choose. The fluid around the rotating impeller blades interacts with the stationary baffles and generates a complex, three-dimensional turbulent flow. Other parameters like impeller clearance from the tank bottom, proximity of the vessel walls, baffle length also affect the generated flow. The geometry of the laboratory and pilot scale reactors used in this simulation are depicted schematically in Figure 5 and the geometrical parameters summarized in Table2 For the reactor, a flat-bottom cylindrical tank with diameter DT = 150 mm and baffles was used. In all simulations, the working fluid was diethylene glycol for ZnO synthesis and 1, 2 butanediol for cobalt/nickel nanowires. Temperature dependant viscosity and mass density of these fluids was considered.
To simulate the exact synthesis conditions a volume of 2.65 liters was considered. This corresponds to a total liquid height of HL = DT = 150 mm. in order to avoid vortex formation and improve the mixing efficiency, four equally spaced baffles with width 16 mm and thickness 5.1 mm were placed on the tank wall.
The three dimensional geometry was created using ANSYS Design Modeler and the mesh was generated by ANSYS Meshing application. The impeller region was further refined in order to better capture the flow phenomena occurring there. The impeller rotation was modeled using the Multiple Reference Frame (MRF) approach, where the computational grid comprised two meshes: an inner cylindrical rotating volume enclosing the impeller and an outer stationary volume forming the rest of the reactor including the baffles and separated by an interface. The interface was defined as an imaginary section to provide the interaction between the rotating and
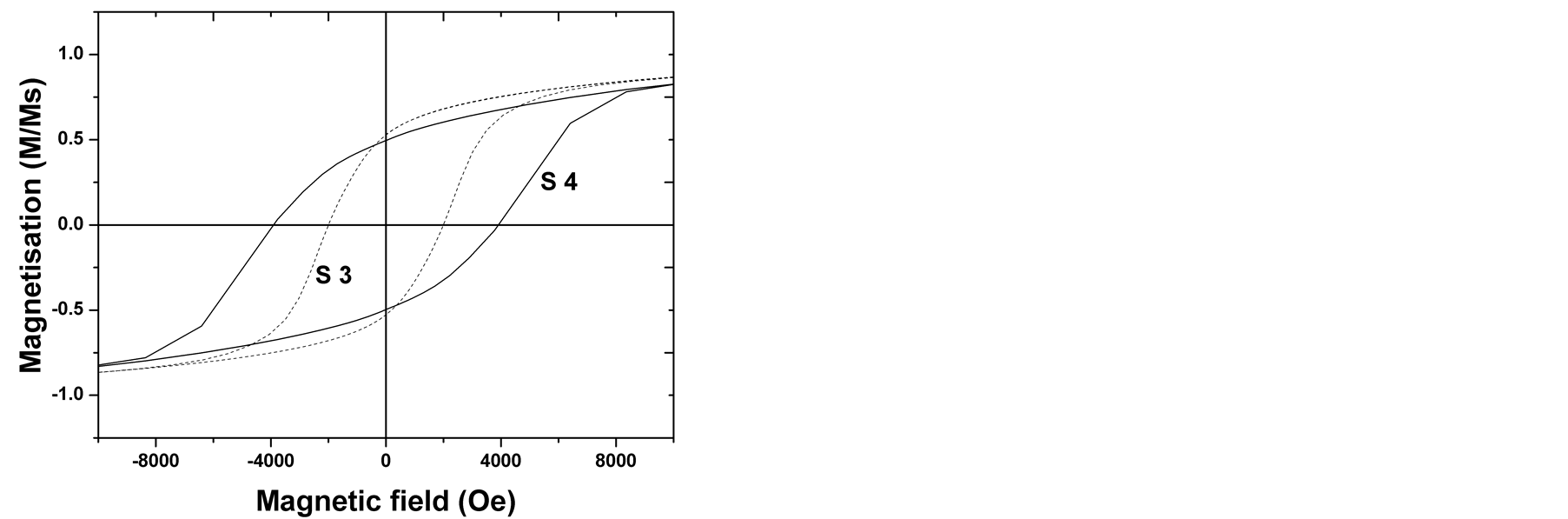
Figure 4. Hysteresis loops of the Co80Ni20 powder recorded at room temperature. (S3) Straight paddle. (S4) Rushton turbine.
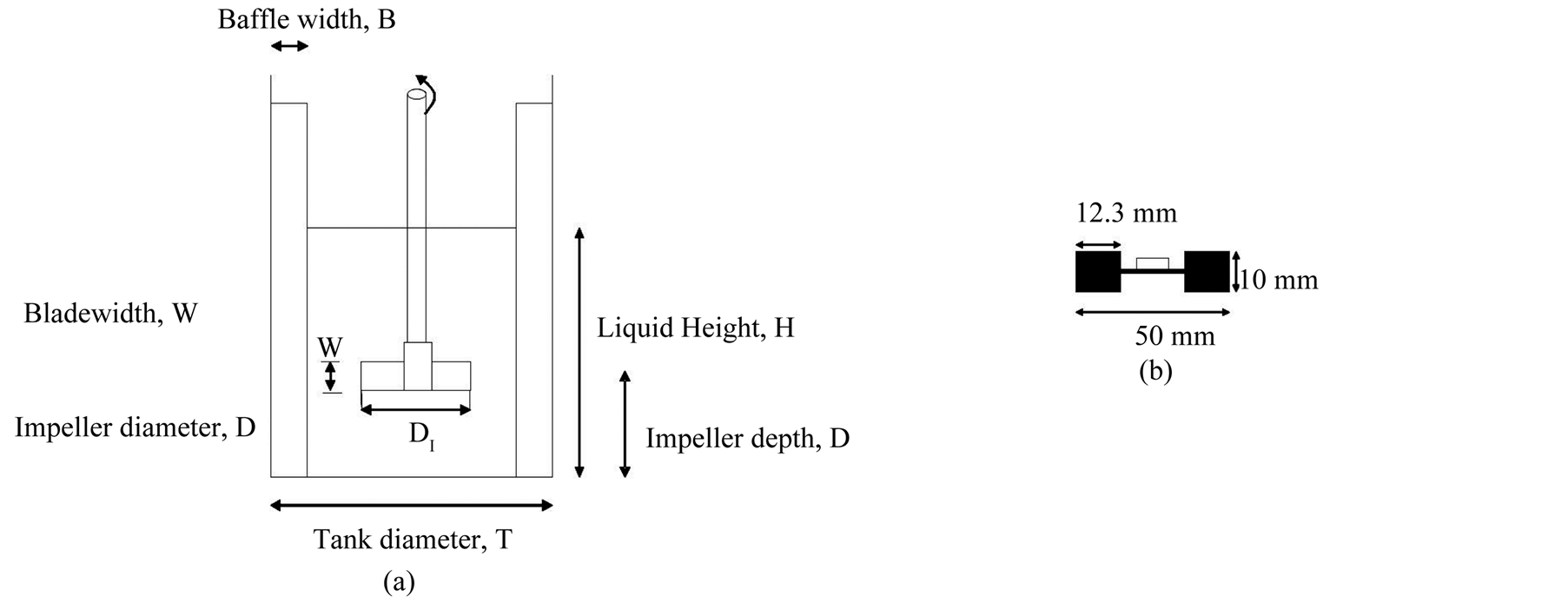
Figure 5. Geometry used in CFD simulation. (a) Straight paddle; (b) Rushton turbine.
stationary frame. Unstructured, non-uniform tetrahedral mesh was generated inside the computational domain. Grids were refined in the wall and impeller regions. After numerous checks for grid sensitivity and mesh constraints, the total number of elements was optimized to provide a computational grid sufficiently fine to resolve the problem within a reasonable CPU time.
The hydrodynamic structure of turbulent flow was then simulated using a three-dimensional
turbulent model. This model employs a fully conservative finite volume method for
the solution of the continuity and momentum equations including turbulence. The
governing equations are given in a Reynolds averaged form of the NavierStokes (RANS)
equations and summarized in Table3 In Equation
(1), Ui is the ith component of the fluid velocity and partial derivatives
with respect to xi that are assumed to one of the three coordinate directions. When
turbulence is included, the velocity is assumed to be the sum of equilibrium and
fluctuating components, Ui and
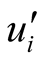 respectively. In Equation (2), the temporal and convection terms are on the left.
Whereas the terms on the right hand side are the pressure gradient; the divergence
of the stress tensor, which is responsible for the diffusion of momentum; the Reynolds
stresses, involving the terms (the over bar indicates that these terms are timeaveraged
values) and the gravitational force, respectively.
respectively. In Equation (2), the temporal and convection terms are on the left.
Whereas the terms on the right hand side are the pressure gradient; the divergence
of the stress tensor, which is responsible for the diffusion of momentum; the Reynolds
stresses, involving the terms (the over bar indicates that these terms are timeaveraged
values) and the gravitational force, respectively.
The governing equations in the flow region surrounding the impeller were modified for the rotating frame. In steady RANS, the time-averaged velocity is resolved and the velocity fluctuations are modeled through turbulence models. The selection of the turbulence approach is critical to fully resolving the fundamentals of the mixing behavior. For solving the Reynolds stresses, the standard k-ε model with enhanced wall treatment was used. This model assumes that the normal stresses are roughly equal and are adequately represented by the turbulent kinetic energy. Two transport equations are used to model the production, distribution, and dissipation of turbulent kinetic energy: the k-Equation (3), and the ε-Equation (4). In Equations (3) and (4), Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients given by Equation (5) where C1ε, C2ε, σk and σε are empirical constants. The turbulent or eddy viscosity, µt is computed by combining k and ε by Equation (6).
The model constants used in our simulations are: C1ε = 1.44; C2ε = 1.92; Cµ = 0.09; σk = 1.0 and σε = 1.3. For initial and boundary conditions, cylindrical wall, bottom wall, and baffles were modeled as stationary, impermeable walls. On these walls a no-slip condition was applied for the liquid. The impeller shaft and hub or discs, in the case of Rushton turbine, were specified as moving walls with angular velocity corresponding to the impeller rotational speed. A free surface boundary condition was defined at the liquid surface. The operating pressure of 1 atm was set at the liquid surface on the top of the tank. As a first approximation, only the pure solvent diethylene glycol or 1,2 Butanediol was considered with temperature dependent mass density µ and dynamic viscosity µ. The impeller shaft and the gravity acceleration were defined along the vertical axis. The impeller rotating speed is set to 220 rpm in all cases. The flow field was calculated using a steady state assumption. The velocity-pressure coupling was achieved using SIMPLE algorithm to iteratively solve the discretized equations. First order upwind discretization scheme was adopted for pressure interpolation and the convective term of momentum and turbulent kinetic energy. The solution residuals for all the conservation Equations (2)-(4) were set to a value of 5 × 10−5. Figure 6 gives the velocity magnitude obtained by the simulation during ZnO synthesis with straight paddle (S1) and Rushton turbine (S2). Similar behaviors were obtained with experiments (S3) and (S4) and are not reported here. For the straight paddle the flow is axial like and the maximum velocity is obtained very close to the impeller at a value of ~1.7 m/s. In contrast, with Rushton turbine, the flow patterns are radial like with a maximum velocity of ~0.8 m/s.
Figure 7 shows the typical contours of the Reynolds number and dissipation of kinetic energy visualized in the transversal plane containing the paddle. The flow field produced by the Rushton turbine is characterized by higher local power dissipation in the impeller zone with the discharge stream of the impeller being mainly radial. By contrast, the straight-type impeller produces a fairly uniform energy distribution throughout the vessel. From these results, two important parameters appear to affect particle size distribution: the flow rates of reagents or Reynolds number (Re) and the energy dissipation (e). Increasing both of them permits to reduce particle size and decreases the distribution width in agreement with several published works [21] -[23] .
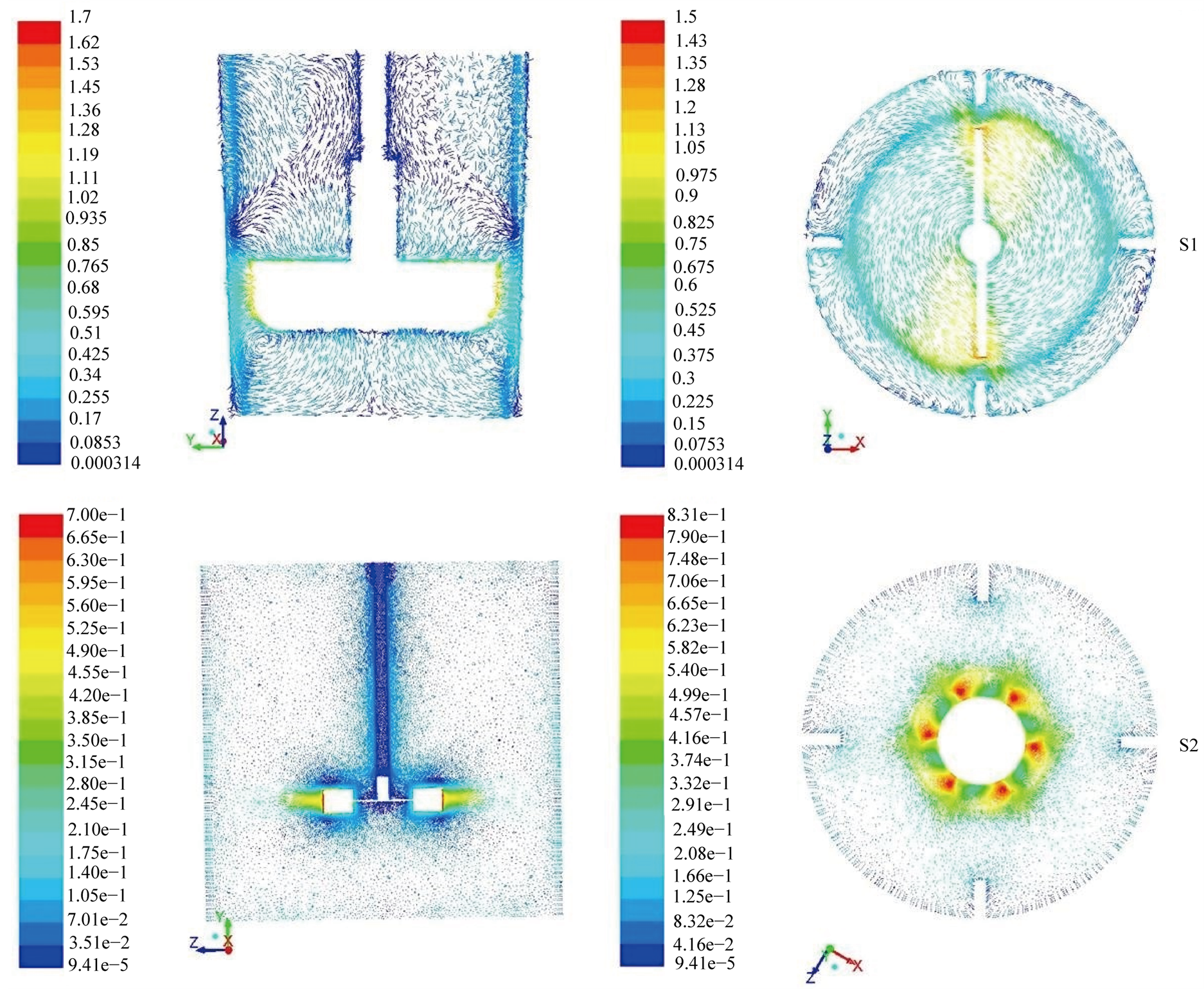
Figure 6. Velocity magnitude in m∙s−1 depicting the flow features in a vertical and horizontal planes in pilot scale with axial (S1) and radial (S2) mixing. Conditions are diethylene glycol as solvent, N = 220 RPM and T = 170˚C.
5. Conclusions
As a conclusion, this study permitted to demonstrate that it is possible to reproduce at larger scale reactors the auspicious conditions for both forced hydrolysis and reduction of metallic salts in polyol medium. We performed the scale-up of these two distinct classes of inorganic nanomaterials in forms of metals and oxides with sample aliquots actually in the tens gram scale. This is useful to elaborate fairly homogenous samples issued from the same batch as already demonstrated in our recent works for photovoltaic applications of zinc oxide [16] and spark plasma sintering (SPS) of cobalt nickel magnetic nanowires [18] [19] .
From fundamental point of view, successful scale-up is possible if shear rate distribution in the reactor is precisely controlled during the synthesis. Nevertheless, the high viscosity and low diffusion coefficients of metallic ions in polyols strongly affect mass transport and reaction kinetics. In order to avoid this negative effect, mixing systems must be optimized to facilitate the reactions by increasing the local dissipated energy. Consequently, it is possible to control local synthesis conditions by choosing the appropriate mixing system that produce nanoparticles with a narrow size distribution. As performed in this paper, CFD calculations could help to depict the turbulent flow patterns and energy dissipation under different impellers geometries giving a better picture of the mixing efficiency in the reaction vessel. Indeed, mixing, which results in bulk movement of the fluid, plays a significant role in maintaining the homogeneity of a given reactive system as well as heat and mass transfers. In the context of large-size reactors, good mixing is especially important since it is essential to maintain the same rate of the mass transfer in to the overall reaction medium thereby insuring uniformly sized and shaped nanopar-

Figure 7. Simulated contours of Reynolds number (Re) and turbulent dissipation of kinetic energy (ε) for ZnO (S1 and S2) and Co80Ni20 (S3 and S4) synthesis. Conditions are DEG at 170˚C for ZnO and 1,2 Butanediol at 165˚C for Co80Ni20. Rotation speed N = 220 RPM.
ticles. The richness of the polyol process associated with chemical engineering methodology could open interesting perspectives for the mass synthesis of several classes of nanomaterials [24] [25] as well as the design of their reactor synthesis from academic-level prototyping to industrial-level manufacturing.
Acknowledgements
IFR Paris Nord Plaine de France (PPF) as well as ANR (Agence Nationale de la Recherche) and CGI (Commissariat à l’Investissement d’Avenir) are gratefully acknowledged for their financial support of this work through Labex SEAM (Science and Engineering for Advanced Materials and Devices) ANR 11 LABX 086, ANR 11 IDEX 05 02.
References
- Figlarz, M., Fiévet, F. and Lagier, J.P. (1985) French Patent No. 8221483.
- Poul, L., Ammar, S., Jouini, N., Fievet, F. and Villain, F. (2003) Synthesis of Inorganic Compounds (Metal, Oxide and Hydroxide) in Polyol Medium: A Versatile Route Related to the Sol-Gel Process. Journal of Sol-Gel Science and Technology, 26, 261-265. http://dx.doi.org/10.1023/A:1020763402390
- Whitney, T.M., Searson, P.C., Jiang, J.S. and Chien, C.L. (1993) Fabrication and Magnetic Properties of Arrays of Metallic Nanowires. Science, 261, 1316-1319. http://dx.doi.org/10.1126/science.261.5126.1316
- Keis, K., Bauer, C., Boschloo, G., Hagfeldt, A., Westermark, K., Rensmo, H. and Siegbahn, H. (2002) Nanostructured ZnO Electrodes for Dye-Sensitized Solar Cell Applications. Journal of Photochemistry and Photobiology A: Chemistry, 148, 57-64. http://dx.doi.org/10.1016/S1010-6030(02)00039-4
- Zauner, R. (1994) Scale-Up of Precipitation Processes. Ph.D. Thesis, University of London, London.
- Gradl, J., Schwarzer, H.-C., Schwertfirm, F., Manhart, M. and Peukert, W. (2006) Precipitation of Nanoparticles in a T-Mixer: Coupling the Particle Population Dynamics with Hydrodynamics through Direct Numerical Simulation. Chemical Engineering and Processing: Process Intensification, 45, 908-916. http://dx.doi.org/10.1016/j.cep.2005.11.012
- Schwarzer, H.-C., Schwertfirm, F., Manhart, M., Schmid, H.-J. and Peukert, W. (2006) Predictive Simulation of Nanoparticle Precipitation Based on the Population Balance Equation. Chemical Engineering Science, 61, 167-181. http://dx.doi.org/10.1016/j.ces.2004.11.064
- Jézéquel, D., Guenot, J., Jouini, N. and Fiévet, F. (1995) Submicrometer Zinc Oxide Particles: Elaboration in Polyol Medium and Morphological Characteristics. Journal of Materials Research, 10, 77-83. http://dx.doi.org/10.1557/JMR.1995.0077
- Dakhlaoui, A., Jendoubi, M., Smiri, L.S., Kanaev, A. and Jouini, N. (2009) Synthesis, Characterization and Optical Properties of ZnO Nanoparticles with Controlled Size and Morphology. Journal of Crystal Growth, 311, 3989-3996. http://dx.doi.org/10.1016/j.jcrysgro.2009.06.028
- Ung, D., Soumare, Y., Chakroune, N., Viau, G., Vaulay, M.J., Richard, V. and Fiévet, F. (2007) Growth of Magnetic Nanowires and Nanodumbbells in Liquid Polyol. Chemistry of Materials, 19, 2084-2094. http://dx.doi.org/10.1021/cm0627387
- Soumare, Y., Piquemal, J.Y., Maurer, T., Ott, F., Chaboussant, G., Falqui, A. and Viau, G. (2008) Oriented Magnetic Nanowires with High Coercivity. Journal of Materials Chemistry, 18, 5696-5702. http://dx.doi.org/10.1039/b810943e
- Soumare, Y., Garcia, C., Maurer, T., Chaboussant, G., Ott, F., Fiévet, F., Piquemal, J.-Y. and Viau, G. (2009) Kinetically Controlled Synthesis of Hexagonally Close-Packed Cobalt Nanorods with High Magnetic Coercivity. Advanced Functional Materials, 19, 1971-1977. http://dx.doi.org/10.1002/adfm.200800822
- Viau, G., Garcia, C., Maurer, T., Chaboussant, G., Ott, F., Soumare, Y. and Piquemal, J.Y. (2009) Highly Crystalline Cobalt Nanowires with High Coercivity Prepared by Soft Chemistry. Physica Status Solidi A, 206, 663-666.
- Liu, Q., Guo, X., Wang, T., Li, Y. and Shen, W. (2010) Synthesis of CoNi Nanowires by Heterogeneous Nucleation in Polyol. Materials Letters, 64, 1271-1274. http://dx.doi.org/10.1016/j.matlet.2010.03.006
- Ait Atmane, K., Zighem, F., Soumare, Y., Ibrahim, M., Boubekri, R., Maurer, T., Margueritat, J., Piquemal, J.-Y., Ott, F., Chaboussant, G., Schoenstein, F., Jouini, N. and Viau, G. (2013) High Temperature Structural and Magnetic Properties of Cobalt Nanorods. Journal of Solid State Chemistry, 197, 297-303. http://dx.doi.org/10.1016/j.jssc.2012.08.009
- Hosni, M., Kusumawati, Y., Farhat, S., Jouini, N. and Pauporté, T. (2014) Effects of Oxide Nanoparticle Size and Shape on Electronic Structure, Charge Transport and Recombination in Dye-Sensitized Solar Cell Photoelectrodes. The Journal of Physical Chemistry C, 118, 16791-16798. http://dx.doi.org/10.1021/jp412772b
- Hosni, M., Farhat, S., Schoenstein, F., Karmous, F., Jouini, N., Viana, V. and Mgaidi, A. (2014) Ultrasound Assisted Synthesis of Nanocrystalline Zinc Oxide: Experiments and Modelling. Journal of Alloys and Compounds, in Press. http://dx.doi.org/10.1016/j.jallcom.2013.12.056.
- Ouar, N., Bousnina, M.A., Schoenstein, F., Mercone, S., Brinza, O., Farhat, S. and Jouini, N. (2014) Spark Plasma Sintering of Co80Ni20 Nanopowders Synthesized by Polyol Process and Their Magnetic and Mechanical Properties. Journal of Alloys and Compounds, in press. http://dx.doi.org/10.1016/j.jallcom.2014.01.058.
- Ouar, N., Schoenstein, F., Mercone, S., Farhat, S., Villeroy, B., Leridon, B. and Jouini, N. (2013) Spark-Plasma-Sintering Magnetic Field Assisted Compaction of Co80Ni20 Nanowires for Anisotropic Ferromagnetic Bulk Materials. Journal of Applied Physics, 114, Article ID: 163907. http://dx.doi.org/10.1063/1.4827199
- Fluent Commercial Software, ANSYS® Version 13.0.
- Bockhorn, H., Mewes, D., Peukert, W. and Warnecke, H.-J. (2010) Micro and Macro Mixing Analysis, Simulation and Numerical Calculation. Springer-Verlag Berlin Heidelberg. http://dx.doi.org/10.1007/978-3-642-04549-3
- Winkelmann, M., Schuler, T., Uzunogullari, P., Winkler, C.A., Gerlinger, W., Sachweh, B. and Schuchmann, H.P. (2012) Influence of Mixing on the Precipitation of Zinc Oxide Nanoparticles with the Miniemulsion Technique. Chemical Engineering Science, 81, 209-219. http://dx.doi.org/10.1016/j.ces.2012.06.036
- Bensaid, S., Deorsola, F.A., Marchisio, D.L., Russo, N. and Fino, D. (2014) Flow Field Simulation and Mixing Efficiency Assessment of the Multi-Inlet Vortex Mixer for Molybdenum Sulfide Nanoparticle Precipitation. Chemical Engineering Journal, 238, 66-77. http://dx.doi.org/10.1016/j.cej.2013.09.065
- He, B., Chen, Y., Liu, H. and Liu, Y. (2005) Synthesis of Solvent-Stabilized Colloidal Nanoparticles of Platinum, Rhodium and Rutheniumby Microwave-Polyol Process. Journal of Nanoscience and Nanotechnology, 5, 266-270. http://dx.doi.org/10.1166/jnn.2005.028
- Jo, Y.H., Park, J.C., Bang, J.U., Song, H. and Lee, H.M. (2011) New Synthesis Approach for Low Temperature Bimetallic Nanoparticles: Size and Composition Controlled Sn-Cu Nanoparticles. Journal of Nanoscience and Nanotechnology, 11, 1037-1041. http://dx.doi.org/10.1166/jnn.2011.3052
NOTES

*Corresponding author.


