Journal of Computer and Communications
Vol.03 No.12(2015), Article ID:61639,8 pages
10.4236/jcc.2015.312001
Identification of Textile Defects Based on GLCM and Neural Networks
Gamil Abdel Azim
College of Computers & Informatics Canal University, Ismailia, Egypt

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 7 October 2015; accepted 29 November 2015; published 2 December 2015

ABSTRACT
In modern textile industry, Tissue online Automatic Inspection (TAI) is becoming an attractive alternative to Human Vision Inspection (HVI). HVI needs a high level of attention nevertheless leading to low performance in terms of tissue inspection. Based on the co-occurrence matrix and its statistical features, as an approach for defects textile identification in the digital image, TAI can potentially provide an objective and reliable evaluation on the fabric production quality. The goal of most TAI systems is to detect the presence of faults in textiles and accurately locate the position of the defects. The motivation behind the fabric defects identification is to enable an on-line quality control of the weaving process. In this paper, we proposed a method based on texture analysis and neural networks to identify the textile defects. A feature extractor is designed based on Gray Level Co-occurrence Matrix (GLCM). A neural network is used as a classifier to identify the textile defects. The numerical simulation showed that the error recognition rates were 100% for the training and 100%, 91% for the best and worst testing respectively.
Keywords:
Image Processing, Neural Network, Gray-Level Co-Occurrence Matrices (GLCM)

1. Introduction
Texture analysis is necessary for many computer image analysis applications such as classification, detection, or segmentation of images. In the other hand, defect detection is an important problem in fabric quality control process. At present, the texture quality identification is manually performed. Therefore, Tissue online Automatic Inspection (TAI) increases the efficiency of production lines and improve the quality of the products as well. Many attempts have been made based on three different approaches: statistical, spectral, and model based [1] .
In this recherche paper, we investigate the potential of the Gray Level Co-occurrence Matrix (GLCM) and neural networks that used as a classifier to identify the textile defects. GLCM is a widely used texture descriptor [2] [3] . The statistical features of GLCM are based on gray level intensities of the image. Such features of the GLCM are useful in texture recognition [4] , image segmentation [5] [6] , image retrieval [7] , color image analysis [8] , image classification [9] [10] , object recognition [11] [12] and texture analysis methods [13] [14] etc. The statistical features are extracted from GLCM of the textile digital image. GLCM is used as a technique for extracting texture features. The neural networks are used as a classifier to detect the presence of defects in textiles fabric products.
The paper is organized as follows. In the next sections, we introduce a brief presentation of GLCM. In section 3, the concept of neural networks with Training Multilayer Perceptrons is described. Image Analysis (Feature Extraction & Preprocessing Data) is given in section 4. Numerical simulation and discussion are presented in section 5; in the end a conclusion is given.
2. Gray-Level Co-Occurrence Matrix (GLCM)
One of the simplest approaches for describing the texture is using a statistical moment of the histogram of the intensity of an image or region [15] . Using a statistical method such as co-occurrence matrix is important to get valuable information about the relative position of neighboring pixels of an image. Either the histogram calculation give only the measures of texture that carry only information about the intensity distribution, but not on the relative position of pixels with respect to each other in that the texture.
Given an image I, N × N, the co-occurrence, and the matrix P defined as:
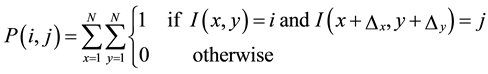 . (1)
. (1)
For more information see [16] .
In the following, we present and review some features of a digital image by using GLCM. Those are Energy, Contrast, Correlation, and Homogeneity (features vector). The energy known as uniformity of ASM (angular second moment) calculated as:
Energy: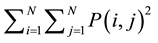 . (2)
. (2)
Contrast measurements of texture or gross variance, of the gray level. The difference is expected to be high in a coarse texture if the gray scale contrast is significant local variation of the gray level. Mathematically, this feature is calculated as:
Contrast: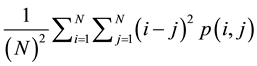 . (3)
. (3)
Texture correlation measures the linear dependence of gray levels on those of neighboring pixels (1). This feature computed as:
Correlation: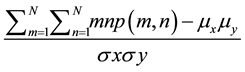 (4)
(4)
where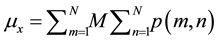 ,
, 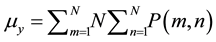
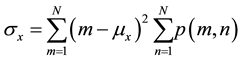
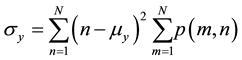 .
.
The homogeneity measures the local correlation a pair of pixels. The homogeneity should be high if the gray level of each pixel pair is similar. This calculated function as follows:
Homogeneity: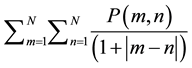 . (5)
. (5)
3. Neural Networks Construction
Artificial neural networks (ANN) are very massively parallel connected structures that composed of some simple processing units nonlinear. Because of their massively parallel structure, they can perform high-speed calculations if implemented on dedicated hardware. In addition to their adaptive nature, they can learn the characteristics of the input signals and to adapt the data changes. The nonlinear character of the ANN can help to perform the function approximation, and signal filtering operations that are beyond optimal linear techniques see [17] -[19] . The output layer used to provide an answer for a given set of input values (Figure 1). In this work the Multilayer Feed-Forward Artificial Neural Networks is used as classifier, where the objective of the back- propagation training is to change the weights connection of the neurons in a direction which minimizes the error E, Which defined as the squared difference between the desired and actual results output nodes. The variation of the connection weight at the kth iteration defined by the following equation:
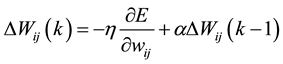 (6)
(6)
where (η) is the proportionality constant termed learning rate and (α) is a momentum term for more information (see [20] -[22] ).
Once the number of layers and the number of units in each layer selected the weights and network thresholds should set so as to minimize the prediction error made by the system. That is the goal of learning algorithms that used to adjust the weights and thresholds automatically to reduce this error (see [23] [24] ).
4. Image Analysis (Feature Extraction & Preprocessing Data)
The feature extraction defined as the transforming of the input data into a set of characteristics with dimensionality reduction. In the other words, the input data to an algorithm will be converted into a reduced representation set of features (features vector).
In this paper, we’re extracting some characteristics of a digital image by using GLCM. Those are Contrast, Correlation, Energy, and Homogeneity. The system was implemented by using MATLAB program. We put the Matlab functions that we utilized in this work between the two <<>>. The proposed system composed of mainly three modules: pre-processing, segmentation and Feature extraction. Pre-processing is done by median filtering <
In the following subsection 4.1, we present a descriptor based on GLCM computation.
4.1. GLCM Descriptorsteps
1) Preprocessing (color to gray, noise, resize (256 × 256));
Figure 1. Feed-forward neural with three layers.
Figure 2. Adjacency of pixel in four directions (horizontal, vertical, left and right diagonals).
2) Segmentation;
3) Feature extraction based on GLCM features using <
4) Concatenation the Contrast, Correlation, Energy and Homogeneity.
The proposed algorithm implemented in MATLAB program developed by the author. After the application of the GLCM descriptor steps (4.1) to the image, we obtained a feature vector of dimension equal to 16 as input for neural networks classifier (Figure 3). The data set divided into two sets, one for training, and one for testing. Preprocessing parameters determined by using a matrix containing all the functionality that used for training or testing; the same settings were used to pre-treat the test feature vectors before transmission to the trained neural network.
A fixed number (m) of examples from each class assigned to the training set and the remaining (m - n) of the testing set. The inputs and targets are normalized, they have means equal zero and standard deviation = 1. The Forward Feed Back-propagation network trained using normalized training sets. The number of inputs of ANN equal to the number of features (m = 16). Each hidden layer contains 2 m neurons and two outputs equal to the number of classes (without defects, with defects) Figure 4 and Figure 5 respectively.
4.2. Simulation and Discussion
We have been developing a real database made by 1500 Images of jeans tissue. Some Images contain defects. The momentum is 0.9 and learning rate is 0.01 ((h, a in the Equation (1)). The ANN output represented by a vector belongs to [0, 1]n. We describe all the features of the training set in a form matrix FM. Each column represents the pattern features. If the training set contains m instances for each model, which belongs to a class, the dimension of the matrix FM is equal to m x n. Where m is the number of features (feature vector size), and n is the number classes. The number of columns 1, 2, 3 … of the matrix FM represents the instance of the model characteristics (textile) that belongs to the class 1. The columns number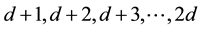 , represents the instance features of the pattern (textile) which belongs to the class 2, etc. (see Figure 6(a) with d = 6 and Figure 6(b) with d = 9).
, represents the instance features of the pattern (textile) which belongs to the class 2, etc. (see Figure 6(a) with d = 6 and Figure 6(b) with d = 9).
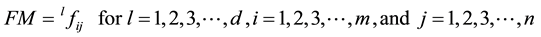 (7)
(7)
[25] and [26] exist more information about the formulation of input and outputs. The accuracy of the system is calculated by using the following equation:
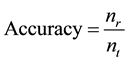 (8)
(8)
where 

Learning set contains six patterns for each category, and the testing set contains nine patterns for each type with accuracy 100%. The system learned with 7 images of each class and tested with 11, 13, 18, 21, 23, 28 images of each category. Figure 7 shows the system accuracy, the best 100% and the worst is 91%. The best 100% results identification obtained when the sizes of each class are 11, 13, and 18.
The system learned with ten images sample of each category and tested with 1, 2… 26 images of each type.
Figure 3. Flowchart of the proposed method.
Figure 4. Example of image without defect.
Figure 5. Example of image with defect.

Figure 6. (a) Neural output matrix with learning set, 6 patterns for class (100%); (b) Neural output matrix with Testing set, 9 patterns for class (100%).
Figure 8 shows the system accuracy, the best is 100% and the worst is 90.5%. We obtained the best results 100% identification when the sizes of class testing are 1, 2 … 15.
Figure 7 shows the correlation between the system accuracy and the size of testing data set. With a given data set of learning, the increasing numbers of patterns in the class for testing lead to decreasing the system efficiency. Increase the rate of the examples used in training to the examples used in the testing implies to increase the rate of recognition.
Figure 7. (a)-(f): Neural output matrix with testing data set are 11, 13, 18, 21, 23, 28 patterns for each class, where the learning data set is 7.
Figure 8. System efficiency with different size of testing data set (1, 2, … , 26), where size of learning data set = 10.
5. Conclusion
We studied and developed an efficient method of textile defects identification based on GLCM and Neural Networks. The descriptor of the textile image based on statistical features of GLCM is used as input to neural networks classifier for recognition and classification defects of raw textile. One hidden layer feed-forward neural networks is used. Experimental results showed that the proposed method is efficient, and the recognition rate is 100% for training and the 100%, 91% best and worst for testing respectively. This study can take part in developing a computer-aided decision (CAD) system for Tissue online Automatic Inspection (TAI). In future work, various effective features will be extracted from the textile image used with other classifiers such as support vector machine.
Cite this paper
Gamil AbdelAzim, (2015) Identification of Textile Defects Based on GLCM and Neural Networks. Journal of Computer and Communications,03,1-8. doi: 10.4236/jcc.2015.312001
References
- 1. Abdel Azim, G. and Nasir, S. (2013) Textile Defects Identification Based on Neural Networks and Mutual Information. International Conference on Computer Applications Technology (ICCAT), Sousse Tunisia, 20-22 January 2013, 98.
http://dx.doi.org/10.1109/ICCAT.2013.6522055 - 2. Davis, L.S. (1975) A Survey on Edge Detection Techniques. Computer Graphics and Image Processing, 4, 248-270.
http://dx.doi.org/10.1016/0146-664X(75)90012-X - 3. Huang, D.-S., Wunsch, D.C., Levine, D.S. and Jo, K.-H., Eds. (2008) Advanced Intelligent Computing Theories and Applications—With Aspects of Theoretical and Methodological Issues. Proceedings of the 4th International Conference on Intelligent Computing (ICIC), 15-18 China, September 2008, 701-708.
- 4. Walker, R.F., Jackway, P.T. and Longstaff, I.D. (1997) Recent Developments in the Use of Co-Occurrence Matrix for Texture Recognition. Proceedings of the 13th International Conference on Digital Signal Processing, Brisbane—Queensland University, 1997.
http://dx.doi.org/10.1109/ICDSP.1997.627968 - 5. Sahoo, M. (2011) Biomedical Image Fusion and Segmentation Using GLCM. International Journal of Computer Application Special Issue on “2nd National Conference—Computing, Communication and Sensor Network” CCSN, 34-39.
- 6. Gonzalez, R.C. and Woods, R.E. (2002) Digital Image Processing. 2nd Edition, Prentice Hall, India.
- 7. Kekre, H.B., Sudeep, D.T., Taneja, K.S. and Suryawanshi, S.V. (2010) Image Retrieval Using Texture Features Extracted from GLCM, LBG and KPE. International Journal of Computer Theory and Engineering, 2, 1793-8201.
http://dx.doi.org/10.7763/ijcte.2010.v2.227 - 8. Haddon, J.F. and Boyce, J.F. (1993) Co-Occurrence Matrices for Image Analysis. IEEE Electronics & Communication Engineering Journal, 5, 71-83.
http://dx.doi.org/10.1049/ecej:19930013 - 9. de Almeida, C.W.D., de Souza, R.M.C.R. and Candeias, A.L.B. (2010) Texture Classification Based on a Co-Occurrence Matrix and Self-Organizing Map. IEEE International Conference on Systems Man & Cybernetics, University of Pernambuco, Recife, 2010.
http://dx.doi.org/10.1109/icsmc.2010.5641934 - 10. Haralick, R.M., Shanmugam, S. and Dinstein, I. (1973) Textural Features for Image Classification. IEEE Transactions on Systems, Man, and Cybernetics, 3, 610-621.
- 11. Flusser, J. and Suk, T. (1993) Pattern Recognition by Affine Moment Invariants. Pattern Recognition, 26, 167-174.
http://dx.doi.org/10.1016/0031-3203(93)90098-H - 12. Lo, C.H. and Don, H.S. (1989) 3D Moment Forms: Their Construction and Application to Object Identification and Positioning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11, 1053-1064.
http://dx.doi.org/10.1109/34.42836 - 13. Srinivasan, G.N. and Shobha, G. (2008) Segmentation Techniques for ATDR. Proceedings of the World Academy of Science, Engineering, and Technology, 36, 2070-3740.
- 14. Tuceryan, M. (1994) Moment Based Texture Segmentation. Pattern Recognition Letters, 15, 659-667.
http://dx.doi.org/10.1016/0167-8655(94)90069-8 - 15. Gonzalez, R.C. and Woods, R.E. (2008) Digital Image Processing. 3rd Edition, Prentice Hall, India.
- 16. Eleyan, A. and Demirel, H. (2011) Co-Occurrence Matrix and Its Statistical Features as a New Approach for Face Recognition. Turkish Journal of Electrical Engineering and Computer Science, 19, No.1.
- 17. Krose, B. and Van Der Smagt, P. (1996) An Introduction to Neural Networks. 8th Edition.
http://www.fwi.uva.nl/research/neuro - 18. Bishop, C. (1995) Neural Networks for Pattern Recognition. Clarendon Press, Oxford, UK.
- 19. Freeman, J.A. and Skapura, D.M. (1991) Neural Networks: Algorithms, Applications and Programming Techniques. Addison-Wesley, Reading.
- 20. Rumelhart, D.E., Hinton, G.E. and Williams, R.J. (1986) Learning Internal Representations by Error Propagation. In: Rumelheart, D.E. and McClelland, J.L., Eds., Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations, MIT Press, Cambridge, 318-362.
- 21. Rumelhart, D.E., Durbin, R. Golden, R. and Chauvin, Y. (1995) Back Propagation: The Basic Theory. In: Chauvin, Y. and Rumelheart, D.E., Eds., Back Propagation: Theory, Architectures and Applications, Lawrence Erlbaum, Hillsdale, 1-34.
- 22. Rumelhart, D.E., Hinton, G.E. and Williams, R.J. (1986) Learning Representations by Back-Propagating Errors. Nature, 323, 533-536.
http://dx.doi.org/10.1038/323533a0 - 23. Patterson, D. (1996) Artificial Neural Networks. Prentice Hall, Singapore.
- 24. Haykin, S. (1994) Neural Networks: A Comprehensive Foundation. Macmillan Publishing, New York.
- 25. Azim, G.A. and Sousow, M.K. (2008) Multi-Layer Feed Forward Neural Networks for Olive Trees Identification. IASTED, Conference on Artificial Intelligence and Application, Austria, 11-13 February 2008, 420-426.
- 26. Kattmah, G. and Azim, G.A. (2013) Fig (Ficus Carica L.) Identification Based on Mutual Information and Neural Networks. International Journal of Image Graphics and Signal Processing (IJIGSP), 5, No. 9.









