Journal of Computer and Communications
Vol.03 No.07(2015), Article ID:57921,11 pages
10.4236/jcc.2015.37001
Elementary Siphons of Petri Nets and Deadlock Control in FMS
Mowafak Hassan Abdul-Hussin
Central Technical Information’s & Communications, University of Technology, Baghdad, Iraq
Email: mow_abdul2007@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 June 2015; accepted 11 July 2015; published 14 July 2015
ABSTRACT
For responsiveness, in the Petri nets theory framework deadlock prevention policies based elementary siphons control are often utilized to deal with deadlocks caused by the sharing of resources in flexible manufacturing system (FMS) which is developing the theory of efficient strict minimal siphons of an S3PR. Analyzer of Petri net models and their P-invariant analysis, and deadlock control are presented as tools for modelling, efficiency structure analysis, control, and investigation of the FMSs when different policies can be implemented for the deadlock prevention. We are to show an effective deadlock prevention policy of a special class of Petri nets namely elementary siphons. As well, both structural analysis and reachability graph analysis and simulation are used for analysis and control of Petri nets. This work is successfully applied Petri nets to deadlock analysis using the concept of elementary siphons, for design of supervisors of some supervisory control problems of FMS and simulation of Petri net tool with MATLAB.
Keywords:
Deadlock Prevention, Siphon, Petri Net, FMSs, PN-Toolbox V. 2.3, S3PR

1. Introduction
A flexible manufacturing system (FMS) is proposed to produce a set of different types of products of varying batch size. It contains a set of computer-controlled machines and transportation systems. Various types of raw components enter it and are processed concurrently. Hence, part resources among various competing jobs have to be carefully controlled and coordinated. For this purpose, a powerful tool for modelling which is called Petri net (PNs) can be used. Petri net is a modelling tool applicable to numerous of FMS.
Petri nets are a favorite tool for depicting and studying information processing systems that are concurrent, asynchronous, synchronous, distributed systems, and reconfiguration structure system. When Petri nets are use of modelling of a real system, a powerful feature of Petri nets is their ability to represent good behavior properties of the system, such as liveness, boundedness, deadlock-free-ness, and reversibility. In FMSs, liveness ensures that deadlocks do not occur. Boundedness guarantees that the number of raw components, buffer spaces and resources is bounded. Reversibility enables the system to return to its initial state, thereby guaranteeing repetitive production. The competition for resources in an FMS may cause it to be deadlocked. In general, a deadlock occurs when the raw components are blocked, while waiting for shared resources held by other production processes.
Abdul-Hussin (2015) [1] studies the synchronization competitive processes to deal with deadlocks caused by the sharing of resources in FMS which is developing the theory for efficient strict minimal siphons for S3PR. An FMS example is used to illustrate the application of the proposed method, and competitive processes are provided in an S3PR to show its superior efficiency. The monitors are used to prevent the presence of unmarked siphons that are the direct causes of deadlocks in such a Petri net. The mathematical computations siphon and trap of Petri net are leading to liveness-enforcing Petri net supervisors with behavior that is more permissive. Petri nets are a modelling and simulation formalism for describing concurrency and synchronization in distributed of FMS.
Abdul-Hussin (2015) [2] presents an approach toward constructing a class structural analysis of Petri nets, where elementary siphon is a main utility used in the development of a deadlock control policy of flexible manufacturing systems (FMSs) that have been exploited successfully for the design of supervisors of some supervisory control problems. Deadlock-free operation of FMSs is significant objectives of siphons in the Petri net. A monitor is added to the plant model such that the siphon is P-invariant-controlled for each elementary siphon, where an integer programming technique is used to guarantee that no emptiable control-induced siphon is generated. The modelling, control and simulation are important topics for both design and operation of FMS. The author [2] has experimental approach based-siphon which is able to resolve the problem of deadlock occurred to Petri nets that are representative of an FMS.
A system of simple sequential processes with resources (S3PR) by Ezpeleta et al. [3] is a powerful Petri net model to describe and analyze the behavior of FMS, and has been adopted widely by many researchers to handle deadlock problems with FMS [1] [3] [4] . Ezpeleta et al. [3] develop a design method of monitor-based liveness Petri net supervisors for FMS, which is usually considered to be a classical contribution that utilizes structural analysis techniques of Petri nets to prevent deadlocks in FMS. The deadlock prevention method can be achieved by adding a control place and related arcs to each strict minimal siphon (SMS), thus the SMS can never be emptied, which guarantees the liveness of the controlled system. There is proposed the relationship between strict minimal siphons and liveness of an S3PR is established. Elementary siphons are first proposed by Li et al. [5] - [7] which are a subclass of SMSs. Apparently, the number is smaller the set of all SMSs. They use the method to control only elementary siphons and prove what the controlled system is live under some conditions.
Huang et al. (2001) [8] propose a strict minimal siphon extraction algorithm such that the complete siphon enumeration is successfully avoided. A shortcoming of their method is that the maximal unmarked siphons need to be computed beforehand, thus the computational efficiency of their method still needs to be improved. Huang et al. (2006) [9] have proposed a deadlock prevention algorithm for S3PR modelled manufacturing systems. The algorithm is an iterative approach based on mixed integer programming (MIP) method [8] . At all iteration, the MIP technique is used to find an unmarked maximal siphon. Next, an unmarked minimal siphon is obtained from the maximal siphon.
Organization. Section 2 provides the preliminaries to be used in this paper. The deadlock control policy is proposed, where is introduced the class (S3PR) of Petri nets models, and the concept of elementary siphons in Section 3. Section 4 presents an FMS example to illustrate the applications of the proposed policy. Section 5 concludes papered.
2. Preliminaries [1] [3]
Definition 1. A Petri net is a 4-tuple Y = (P, T, E, W), where P, and T are finite nonempty, and disjoint sets. P is a set of places, and T is a set of transitions with P È T ≠ Æ, and P Ç T = Æ. E Í (P ´ T) È (T ´ P) is called a flow relation or the set of directed arcs. The net has represented by arcs with arrows from places to transitions or from transitions to places. W: E ® Z+ is a mapping that assigns a weight to any arc, where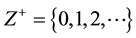 . Y = (P, T, E, W) is ordinary, denoted as Y = (P, T, E, W), (When Weights W, of the arcs (W) = l, the net Y is called ordinary Petri net). The Weights W: (P ´ T) È (T ´ P) ® Z+ is a mapping that assigns a weight to an arc: W(x, y) > 0 if (x, y) Î E, and W(x, y) = 0 otherwise, where x, y Î P È T and Z+ denote the set of non-negative integers.
. Y = (P, T, E, W) is ordinary, denoted as Y = (P, T, E, W), (When Weights W, of the arcs (W) = l, the net Y is called ordinary Petri net). The Weights W: (P ´ T) È (T ´ P) ® Z+ is a mapping that assigns a weight to an arc: W(x, y) > 0 if (x, y) Î E, and W(x, y) = 0 otherwise, where x, y Î P È T and Z+ denote the set of non-negative integers.
Definition 2. In the absence of self-loops, an equivalent information is given by the incidence matrix. The computation of the incidence matrix C is subtracting C− from C+ that is: C = (C+ − C−) or
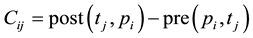 . A Petri net Y = (P, T, E, W) can be alternatively represented by its flow matrix or incidence C = (Cij) which is defined by:
. A Petri net Y = (P, T, E, W) can be alternatively represented by its flow matrix or incidence C = (Cij) which is defined by:
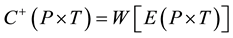 and
and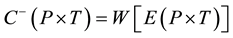 . In addition, we can write
. In addition, we can write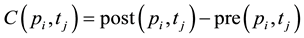 , is the change in matrix C, where incidence matrix [C] of net Y is a |P| × |T| integer matrix and
, is the change in matrix C, where incidence matrix [C] of net Y is a |P| × |T| integer matrix and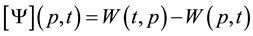 .
.
Definition 3. The preset of a node
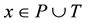 is defined as
is defined as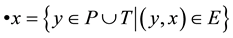 . While the post-set of a node
. While the post-set of a node
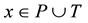 is defined as
is defined as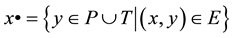 . This notation can be extended to a set of nodes as: given
. This notation can be extended to a set of nodes as: given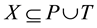 ,
,
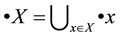 and
and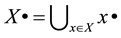 . A marking is a mapping M: P ® Z+, where Z+ È
. A marking is a mapping M: P ® Z+, where Z+ È
{0}. M(p) denotes the number of tokens in place p. The preset (postset) of a set is defined as the union of the presets (postsets) of its elements. The pre- and post-sets of a transition t Î T are defined respectively as:
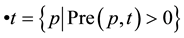 , and
, and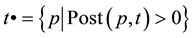 . The pre- and post-sets of a place p Î P are defined respectively as:
. The pre- and post-sets of a place p Î P are defined respectively as:
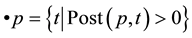 and
and
Definition 4. The pair (Y, M0) is called a marked Petri net or a net system. The set of markings reachable from M in Y is denoted as R(Y, M). A net (Y, M) is bounded if and only if (iff) $k Î Y, "M Î R(Y, M0), "p Î P, M(p) ≤ k holds. A transition t Î T is enabled under M, denoted by M[tñ, iff "p Î ∙t, M(p) ≥ 1. A transition t Î T is live under M0 iff "M Î R(Y, M0), $M Î R(Y, M0), M'[tñ holds. (Y, M0) is deadlock-free iff "M Î R(Y, M0), ∃t Î T, M[tñ holds. (Y, M0) is live iff "t Î T, t is live under M0.
Definition 5. A transition t is said to be live if for any M Î R(Y, M0), there exists a sequence of transitions that is fired to lead next marking M' that enables at transition t. A PN is said to be live if all the transitions are live. A PN contains a deadlock if there is a marking M Î R(Y, M0), at which no transition is enabled. Such a marking is called a dead marking. Deadlock situations are because of in appropriate resource allocation policies or exhaustive use of some or all resources. Liveness of a PN means that for each marking M Î R(Y, M0) reachable from the M0, it is finally possible to fire t, "t Î T through some firing sequence. A net (Y, M0) is said to be reversible, if "M Î R(Y, M0), M0 Î R(Y, M). Therefore, in a reversible net it is always possible to go back to initial marking M0. A marking M' is said to be a home state, if for each marking M Î R(Y, M0), M' is reachable from M. Reversibility is a special case of the home state property. If the home state M' = M0, then the net is reversible.
Definition 6. A sequence of transitions



Definition 7. A P-vector is a column vector I: P → Z indexed by P, where Z is the set of integers. I is a P-invariant (place invariant) if and only if I ≠ 0 and IT × [Y] = 0T holds. P-invariant I is said to be a P-semiflow
if every element of I is non-negative.

(Y, M0) then "M Î R(Y, M0): IT × M = IT× M0. In an ordinary net, siphon S is controlled by P-invariant I under
M0 if and only if (IT × M0 > 0) and
Definition 8. Let S A non-empty sub-set of places. S Í P is a siphon (trap) iff ∙S Í S∙ (resp. Q∙ Í ∙Q). A siphon is said to be minimal iff there is no siphon contained in S it as a proper subset. A minimal siphon that does not contain the support of any P-invariant is called a strict minimal siphon (SMS). A siphon S is controlled iff it can never be emptied. It is said to be invariant-controlled by P-invariant I if IT × M > 0 and ||I||+ Í S.
Definition 9. A PN is live under M0 iff "t Î T, t is live under M0. A transition t Î T is live under M0 iff "M Î R(Y, M0), $M' Î R(Y, M0), t is friable under M'. A transition t Î T is dead under M0 if

Definition 10.(Conservative). A Petri Net PN with initial marking M0 is strictly conservative, if for all markings M, elements of the Reachability set R(M0), the number of tokens remains constant, i.e. A marked Petri net
Y = (Y, M0), is said to be conservative iff :


A P-invariant characterizes a token conservation rule for a set of places, over which the weighted sum of tokens is constant independently from any firing, i.e., for a p-invariant x and any markings Mi, Mj Î Yn, which are reachable from M0 by the firing of transitions, it holds. XT × M = XT × M0.
Definition 11. The Pre- and Post-incidence matrix of net Y can be represented as (n ´ m) matrix, Pre-and Post with elements Pre(pi, tj), and Post(pi, tj), respectively. The linear algebraic analysis method uses the description of a Petri net by its so called incidence matrix C = (Cij) which is defined by:



matrix of a net is a matrix with |P| rows and |T| columns defined as pre (P × T) ® {−1, 0, 1} such that pre(p, t) is (+1) if (t, p) Î E, (−1) if (p, t) Î E, and 0 otherwise. The state changes of a PN occur when a transition t is fire. These changes can be representing in an algebraic form using the state equation given by: M1 = M0 + post(p, t) − pre(p, t).
Example 1. An example of a Petri net is shown in Figure 1. Places are circles and transitions by rectangles or bars. This is the convention, which has been adopted for ordinary Petri nets when the weight of arcs equals to one. To design a controller to avoid deadlock, it is necessary to find the strict minimal siphons as: S1 = {p1, p3, p4}, and S2 = {p1, p2, p4}. The strict minimal trap as Q1 = {p1, p4, p5}, and Q2 = {p1, p3, p4}. Siphons are very important in the analysis and control of deadlocks in a Petri net. Any Petri Net can be representation as an incidence matrix. The Petri net of Figure 1 has the following incidence matrices shown in Figure 2.

Figure 1. Shows a simple example of a Petri net.

Figure 2. Incidence matrix of Figure 1.
An important practical, applied definition (6) (linear state equation) is a Petri net a transition t of an ordinary. Petri net is enabled if and only if each of its input places contains at least one token. In this example represented in Figure 1, the initial marking M0 = [1, 0, 1, 0, 1]T and the following transitions can be fired starting from M0.
Applied definition (6), the state equation is: M¢ = M0 + C × sti , and taking the column vector of firing transition from the incidence matrix on Figure 2. The marking evolve M1 = [0, 1, 1, 1, 1]T, after the firing of t1. Such that M1 = M0 + C × st1 = M0 [1, 0, 1, 0, 1]T + column t1 from matrix Figure 2, [-1, 1, 0, 1, 0]T = M1 = [0, 1, 1, 1, 1]T = M1. For each of these new marking is representing a node of the reachability tree and used the next state at firing transition. In the sequel, the next marking can be found by adding last marking to the column of transition shown in Figure 2, where transition t1 is enabled. The new marking M2 = M1 + C × st2 = [0, 1, 1, 1, 1]T + [0, -1, -1, 1, 0]T = [0, 0, 0, 2, 1] = M2. The next firing transition is t3, M3 = M1 + C × st3 = [0, 1, 1, 1, 1]T + [1, 0, 0, -1, -1]T = [1, 1, 1, 0, 0] = M3. The deadlock is occurring at transition t4, the marking M9 = [0, 0, 2, 0, 3] as shown in Figure 3, in the red colored. The remainder of the mathematical computation of the net in Figure 1, can be analytically in the reachability tree of a Petri net is shown in Figure 3, where are used Petri net tool for MATLAB, (Toolbox PN-Tool 2.3) [10] .
Additional place V1, called control place in order to controlled siphon of the net. The simulation and structure analyses of this example are provided to illustrate the feasibility and effectiveness of siphon controlled by adding a monitor that can be enforced on the net dynamics by the addition of a “control” or “monitor” place to the original net structure.
We have predicted a deadlock with a look-ahead Petri net controller. The connections of control places V1is in the red colored in Figure 4. The resulting controlled Petri net is shown in Figure 5. It can be verified that deadlock does not occur in this Petri net. In the Figure 1, the minimal siphon whose emptiness leads to the deadlock of the net shown in Figure 3. To control the net prevented from being unmarked, a place V1 is added with ×V1 = {t3} and V1× = {t4}, as shown in Figure 4, in order to the control is a Petri net in Figure 1. The effecting controlled place in Petri net is shown in Figure 5. It can be verified that deadlock does not occur in this Petri net.
3. Deadlock Prevent Policy
Deadlock prevention policy is dealing with a special class of Petri nets, which is a subclass of ordinary and conservative Petri nets called S3PR. In this a section, we introduced some definitions have been needed for our application for a deadlock prevention policy that can keep the system in deadlock-free for a class of Petri nets, which is called S3PR nets.

Figure 3. Reachability tree is non-live in PN-Toolbox with MATLAB [10] of Figure 1.

Figure 4. Siphon control examples 1.

Figure 5. The coverability tree is live of Figure 4.
3.1. The Class of the S3PR Nets
The class of Petri nets investigated in this research is an S3PR that is first proposed in Ezpeleta et al. [3] . The presentation of its formal definitions is needed for our application. The following results are mainly from [3] [4] .
Definition 12. A simple sequential process (S2P) is a Petri net Y = (PA È {p0}, T, E), where the following statements are true:
1) PA ¹ Æ is called a set of operation places;
2) p0 Ï PA is called the process idle place;
3) A net Y is a strongly connected state machine; and
4) Every circuit of Y contains place p0.
Definition 13. Let Yi = (PA È P0 È PR, T, E) be an S3PR. An initial marking M0 is called an acceptable one if: 1) "p Î P0, M0(p) ≥ 1; 2) "p Î PA, M0(p) = 0; and 3) "p Î PR, M0(p) ≥ 1.
3.2. Elementary Siphon in Petri Nets
The concepts elementary and dependent siphons are original work by Li et al. [5] - [7] . They are developed the Petri nets theory of computation and powerful mathematics. We have introduced the concept of elementary and dependent siphons as well as used in this paper.
Definition 14. Let S Í p is a subset of places of Petri net Y = (P, T, E, W). P-vector lS is called the characteristic P-Vector of S if and only if "p Î S, lS(p) =1; otherwise lS(p) = 0.
Definition 15. Let hS is characteristic T-Vector of S if and only if hST = lST = [Y].
Definition 16. Let S Í P is a subset of places of Petri net Y. hS is characteristic T-Vector of S if and only if hS = lST∙[C], where C is incidence matrix of Y.
Definition 17. Let Y = (P, T, E, W) is a net with |P| = m, |T| = n, and K siphons S1 - Sk,
Definition 18. Let


Definition 19. Let S Ï PE be a siphon in net Y. Then S is called a strongly dependent siphon if


Theorem 1. Let YES be the number of elementary siphons in Y = (P, T, E, W). Then we have YES < min{|P|, |T|}. This result indicates that the smaller of a place and transition counts bound the number of elementary siphons in a net.
Theorem 2. Let S be a siphon if net Y = (P, T, E, W) and hS be its characteristic T-vector. We can conclude that {t Î T|hS(t) > 0}, {t Î T|hS(t) = 0}, and {t Î T|hS(t) < 0} are a sets of transitions that is firings will increase, maintain, and decrease the number of tokens marked in S respectively.
4. Application of Petri Net Modelling in FMSs
Let us assume the small FMS have shown in Figure 6. The system consists of two robots, R1 and R2, each of

Figure 6. Layout of a manufacturing cell of FMS.
which can hold one part at a time, and three machines, M1, M2, and M3. The machine M1 can process only one part at a time, while M2 and M3 can process two parts at a time. Parts enter into the FMS through input/output buffers I1/O1 and I2/O2. In the situation, we consider that there are two part types J1 - J2, can be produced in this system. The production routing of J1 is: I1 ® R1 ® M1 ® O1 or I1 ® R1 ® M2 ® R2 ® M3 ® O1. The production routing of J2 is I2 ® M3 ® R2 ® M2 ® O2.
The S3PR Petri net with 15 places and 11 transitions depicted in Figure 7, which has been considered in the literature (see [3] [6] [8] ). We are choice of different approach to structure and initial markings in order to find out different sets of siphons, and have experienced, and application to show the efficient methods the concept of, elementary and dependent siphons in an S3PR can be controlled net.
The Petri net model of the FMS is shown in Figure 7, in which places p3, p4, p9, p10, p11, denote R1, M1, M2, R2, and M3, respectively. Places p1 and p15 are idle places, and p2, p5, p6, p7, p8, are operation places for production Line_1. Places p12, p13, and p14 are operation places for production Line_2. The Petri net shown in Figure 7 is represented an S3PR by this place specification.
Figure 7 shows the Petri net model of FMS. Places p2 and p5 represent the operation of R1, and M1, respectively, for the production sequence of the part type_P1. Similarly, places p2, p6, p7 and p8 represent the operation of R1, M2, R2 and M3 respectively, for the production sequence of the part type P1. The production sequence of the part type_P2, places p12, p13 and p14 represent the operation of M3, R2 and M2 respectively. The number of tokens in Figure 7, M0 is an acceptable initial marking if M0(p1) = 3, M0(p15) = 5, M0(p9) = M0(p11) = 2, M0(p3) = M0(p4) = M0(p10) = 1, and others are zero.
For the Petri net of Figure 7 is an S3PR. The elements of this net are defined as: Figure 7.



We can be found out the strict minimal siphons. In the Petri net shown in Figure 7, has 10 minimal siphons:










The set of siphons from S4 - S10 is both a siphon and a trap. We have choice strict minimal siphons S1, S2, and

Figure 7. An S3PR (Y, M0) [3] .
S3 that do not contain any trap. The strict minimal siphons are as:



We have three the strict minimal:



The computation of S1 and S2 is leading to determinate the third control place S3 from the account accumulation of S1 and S2 is the linearly independent vectors can be constructed in [η] shown as follows.



The T-vector matrix can be strutted in [η] shown as follows:
Therefore, the siphons that correspond to the first and second rows are elementary siphons. Next, we can compute the dependent siphons as: hS3 = hS1+ hS2 . Thus, S1 = {p8, p10, p11, p13}, and S2 = {p7, p9, p10, p14}, are elementary siphons and S3 = {p8, p9, p10, p11, p14}, is a strict dependent siphon. The elementary siphons are ΠE = (S1, S2), and the dependent siphons ΠD = (S3), and S3 is a strongly dependent siphon.
We are representing here a structural analysis method including the following verification on the specification of the elementary siphon of the algorithm found in [6] - [8] , and S1 and S2 are elementary siphons in the net for the deadlock control purpose. Therefore, we are connected control place VS1 to the transition, where: ∙VS1 = {t6, t9}, VS1∙ = {t5, t8}, and ∙VS2 = {t4, t5, t10}, VS2∙ = {t1, t3, t8}. We can be adding two controls place in the original net. While the third control place is not necessary to add because the simulation of Petri net in Figure 8, do not affected results. The resulting control policy is overly restrictive only, and reachability graph has reduced to 15 states as show in Figure 9.

Figure 8. Control place VS1, and VS2, are control net Figure 7.

Figure 9. Represented coverability tree is liveness of Figure 8.
This is successfully resulted when comparison purposes with the other researcher such as: Ezpeleta et al. [3] computes three control places and has only 28 reachable marking. The method in [6] classifies S1 and S2 as elementary siphons and S3 as strictly dependent. Then, only two controls places are necessary, which actually coincide with the first two control places added by the previous method. In addition, this work has only 28 markings be reachable in the controlled net. The method of Huang et al. (2001) [8] proposed to require three control places, one of which connected with weighted arcs that the controlled net is not ordinary: The controlled net has only 44 reachable markings. In our experiment, we can add two-controlled net has only (15) reachable markings show in Figure 9, without needing third control places, because, the result is not affected to the net (i.e. some results).
The additional controlled places net of Figure 8, is live and obtain to marking M14, and has 15 reachable states marking, so that the Petri net is deadlock-free actually liveness. Siphons are generating even though the monitors are added. An experiment is carried on encouragement one to discover the technicality to make a siphon powerful to control by adding control places (monitor). The result of the efficient structural analysis of Petri nets, because the PN-Toolbox with MATLAB [10] can show the PN shape of the simulation is accurate and correct results.
Let us show the Petri net is modelled in Figure 8. According to definition 7, there are three minimal siphons, which can be emptied. There are S1 = {p8, p10, p11, p13}, S2 = {p7, p9, p10, p14}. For the purpose control place VS1 is added such that I1 = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1VS1) is a P−invariant of (Y1, M1). Therefore, I1 × M1 = 0 by definition 7, we can compute that [(Y1](VS1, t) = − t5 + t6 − t8 + t9. Similarly, I2 = (0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1VS2) is also a P−invariant of (Y1, M1). Hence (I2 × M1) = 0, and [Y1](VS2, t) = − t1 − t3 + t4 + t5 − t8 + t10, than reachability tree reachable to M14 as shown in Figure 9.
For elementary siphons S1 and S2, three monitor VS1 and VS2 are added respectively to the net. We can apply definition 7, to find a P-invariant controlled of the Petri net depending of the incidence matrix existing in Figure 10, implementation manuals.
Petri net incidence matrix and P-invariant
Figure 10. The incidence matrix of Figure 8, and P-invariant.
Figure 10. The incidence matrix of Figure 8, and P-invariant.
For instance, Figure 8 has shown an S3PR net. S1 = {p8, p10, p11, p13} is a siphon of the net. We can apply definition 7, to find a P-invariant of the net in Figure 10. This is: I1 = (0, −1, −1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, −1VS1)T = (−p2 − p3 + p8 + p10 + p11 + p13 − VS1) is a P-invariant of (Y1, M1). Where, IT × M0 = M(p8) + M(p10) + M(p11) + M(p13) − M(p2) − M(p3) − M(VS1) = 1 > 0. So that ||I1||+ = {p8, p10, p11, p13} Í S. Thus, S1 = {p8, p10, p11, p13} is an invariant-controlled siphon and it can never be emptiable. Similarly, for S2 = {p7, p9, p10, p14} is a siphon of the net. Also, I2 = (1, 0, 0, 0, 0, 1, 1, 0, 1, 1, −1, −1, 0, 1, 0, −1VS1 − 1VS2)T = {p1 + p6 + p7 + p9 + p10− p11 − p12 + p14 − VS1 − VS2} is a P−invariant of (Y1, M1). Where, IT × M0 = {M(p1) + M(p6) + M(p7) + M(p9) + M(p10) − M(p11) − M(p12) + M(p14)− M(VS1) − M(VS2)} = 1 > 0. So that: ||I2||+ = {p7, p9, p10, p14} Í S, is an invariant-controlled siphon and it can never be emptied.
In addition, there are five resources in this system of Figure 7, leading to five minimal P-invariants, we would like to mention as follow:










This has been done with a Laptop computer, Intel(R) Core(TM) i5-3337U CPU@ 1.80GHz, with 4Gb of RAM, with Windows 7 Ultimate.
5. Conclusion
Petri net is possible to represent of FMS that can be simulation and analysis is supported by different visualization and interaction techniques to capture the properties such as strict minimal siphons, and behaviour of Petri nets quickly (e.g. interactive behavior, interactive exploration of invariants and the reachability graph). We are developing a guarantees tool for Petri net based to siphon, simulation and structural analysis dealing with the (FMS). Some control places and related arcs are added to minimal siphons such that no siphon can be emptied. A Petri net is efficient techniques to enumerate and reduce the reachability graph by adding monitors to all basic siphons and only those compound siphons. The reachability graph is reduced to explain the necessary evolutionary behavior of the PN regarding liveness and deadlocks. Based on Petri nets, a deadlock prevention policy is proposed to a special class of Petri nets called (S3PR).
Cite this paper
Mowafak HassanAbdul-Hussin, (2015) Elementary Siphons of Petri Nets and Deadlock Control in FMS. Journal of Computer and Communications,03,1-12. doi: 10.4236/jcc.2015.37001
References
- 1. Abdul-Hussin, M. (2015) Synchronization Competitive Processes of Flexible Manufacturing Systems Using Siphons Petri Net. Proceedings of IEEE the 5th National Symposium on Information Technology: Towards New Smart World 2015, Human-Robot Interaction, Riyadh, 16 February 2015, 6 p.
- 2. Abdul-Hussin, M.H. (2015) A Structural Analysis of Petri Nets-Based Siphons Supervisors of Flexible Manufacturing Systems. Proceedings of IEEE-UKSim-AMSS, 17th International Conference on Computer Modelling and Simulation, Cambridge University, (Emmanuel College), Cambridge, March 2015, 235-241.http://uksim.info/uksim2015/data/8713a235.pdf
- 3. Ezpeleta. J., Colom, J.M. and Martinez, J. (1995) A Petri Net Based Deadlock Prevention Policy for Flexible Manufacturing Systems. IEEE Transactions on Robotics and Automation, 11, 173-184.
http://dx.doi.org/10.1109/70.370500 - 4. Wang, S.G., Zhou, M.C. and Wu, W.H. (2015) Design of a Maximally Permissive Liveness-Enforcing Supervisor with Reduced Complexity for Automated Manufacturing Systems. Asian Journal of Control, 17, 190-201. http://dx.doi.org/10.1002/asjc.837
- 5. Li, Z.W. and Zhou, M.C. (2004) Elementary Siphons of Petri Nets and Their Application to Deadlock Prevention in Flexible Manufacturing Systems. IEEE Transactions on System Man, and Cybernetic. Part A: System and Humans, 34, 38-51. http://dx.doi.org/10.1109/TSMCA.2003.820576
- 6. Li, Z.W. and Zhou, M.C. (2008) Control of Elementary and Dependent Siphons in Petri Nets and Their Application. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 38, 133-148. http://dx.doi.org/10.1109/TSMCA.2007.909548
- 7. Li, Z.W. and Zhou, M.C. (2009) Deadlock Resolution in Automated Manufacturing Systems: A Novel Petri Net Approach. Springer, London.
- 8. Huang, Y.S., Jeng, M., Xie, X. and Chung, S. (2001) Deadlock Prevention Policy Based on Petri Nets and Siphons. International Journal of Production Research, 39, 283-305.
http://dx.doi.org/10.1080/00207540010002405 - 9. Huang, Y.S., Jeng, M., Xie, X.L. and Chung, D.-H. (2006) Siphon-Based Deadlock Prevention Policy for Flexible Manufacturing Systems. IEEE Transactions on Systems, Man and Cybernetics, Part A, 36, 1248-1256. http://dx.doi.org/10.1109/TSMCA.2006.878953
- 10. Mahulea, C., Matcovschi, M.H. and Pastravanu, O. (2003) Home Page of the Petri Net. Petri Net Toolbox with MATLAB Version 2.3. http://www.ac.tuiasi.ro/pntool


