Journal of Applied Mathematics and Physics
Vol.04 No.11(2016), Article ID:71909,12 pages
10.4236/jamp.2016.411198
Observing the Jumping Laser Dogs
Alberto Tufaile1*, Timm A. Vanderelli2, Adriana Pedrosa Biscaia Tufaile1
1Soft Matter Laboratory, Escola de Artes, Ciências e Humanidades, Universidade de São Paulo, São Paulo, Brazil
2Ferrocell USA, 739 Route 259, Ligonier, PA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 27, 2016; Accepted: November 7, 2016; Published: November 10, 2016
ABSTRACT
Jumping sun dogs are rapid light flashes changing over clouds, with some of them located close to the places of halo formation in thunder storms clouds. This paper presents an outline of some aspects that are required for understanding the jumping sun dogs, using some experiments with light scattering in complex fluids. In our analogy, we have observed the jumping laser dogs, in which the ice crystals are replaced by needlelike structures of ferrofluid, the electric field in the atmosphere is represented by an external magnetic field, and the laser beam scattered by the ferrofluid structure has the same role of the sun as the source of light scattered by the ice crystals subjected to changing electric fields in thunderstorm clouds.
Keywords:
Diffracted Rays, Sun Dogs, Laser Dogs, Geometrical Theory of Diffraction

1. Introduction
In the past few years, some people have reported the occurrence of a bizarre phenomenon: the observation of rapid light flashes changing over clouds, with some of them located close to the places of halo formation in thunderstorms clouds, as it is shown in Figure 1, like the motion of a “giant light saber”. These phenomena were observed by accident in the sky, and because of these reports, some researchers have suggested the hypothesis that these phenomena could be related with jumping sun dogs [1] [2] .
It has been known for sometime that the light scattering in the ice crystals in a cloud is related to the optical effects like halos and sun pillars, and this hypothesis holds that a lightning discharge in a thundercloud can temporally change the electric field above the cloud where charged ice crystals are reflecting sunlight, and these changes in the electric fields reorient the ice crystals to a new position that scatters sun light differently [3] , creating a visual cloud streamer [4] . In this way, we consider that the system
Figure 1. The jumping sun dog phenomenon is shown in these pictures. At the top, in the general view perspective, we can see the thunderstorms clouds with the light flash at the left side of the picture. The luminous white column is swung back and forth at the frequency approximately of 1 Hz during 1 minute, combining fast and slow motions, presented in the pictures at bottom. Pictures obtained from Youtube user QUADME13 using the camera of a smartphone in 2015, Greenwood, Indiana, USA.
present in the atmosphere acts as a complex fluid interacting with sun light, in which a mixture of solid phase (ice crystals) and gas phase (air/water vapour) [5] shows the evidence of unusual responses to the applied electric field, creating jumping sun dogs or crown flashes. Based on our previous papers, we are suggesting that some these jumping sun dogs are related with the parhelic circle. Like the jumping sun dogs, the parhelic circle is mainly white, and the absence of separated colors could indicate a different kind of light scattering, not only light refraction.
The aim of this paper is thus to explore some patterns obtained by light scattering in a complex fluid and comparing them with the jumping sun dogs. In order to accomplish our goal, we have used a device known as Ferrocell, which consists in a Hele-Shaw cell containing a ferrofluid suspension of ferromagnetic nanoparticles that will be explained in Section 2. The scattering of light in the Ferrocell can create diffracted rays, and in a recent work, we have shown that the formation of sun dogs, sun pillars, and the parhelic circle could be related to these diffracted rays, using the Geometrical Theory of Diffraction (GTD) [6] [7] [8] . In Section 3, we present some properties of light polarization in the light scattering with the Ferrocell, which plays the role of the atmosphere in our analogy. We report the simulation of the jumping sun dogs using the Ferrocell in Section 4. Finally, we present our conclusions in Section 5.
2. Experimental Apparatus
This experiment is essentially the light scattering in ferrofluid, and our atmosphere is the colloidal suspension of nanoparticles inside the Ferrocell. The ferrofluid is a stable colloidal dispersion using light mineral oil.
In order to explore the effects of the light scattering in the Ferrocell subjected to an external magnetic field, we have used two different types of light source configurations, the setup 1, for the observation of polarized light effects, and the setup 2, for the case of laser beam scattering obtaining the jumping laser dogs, represented in Figure 2.
In the setup 1, a white light source was generated using a LED panel light (12 W), illuminating over the complete surface of a square Ferrocell (22 mm × 22 mm) homogeneously, with a methacrylate diffuser and backlighting technique. Just for this case, the Ferrocell was placed between two crossed polarizers, as it is shown in Figure 2(a). The glass plates used in the Ferrocell in this case are microscope slides. The image is obtained directly from the system polarizers/Ferrocell.
The setup 2 uses a circular Ferrocell made up of two 58.5 mm diameter glass plates, represented in Figure 2(b). For this case, the light source is a green diode laser (10 mW) with a wavelength of 532 nm. The beam width is around 2,00 mm. Once the beam reaches the Ferrocell, part is reflected, and part is transmitted, scattering the light. The image formed by reflection and transmission of light scattering is projected onto a screen, and a digital camera is used as a light detector of the patterns observed in the experiment.
Figure 2. In (a) the square Ferrocell1 used in setup 1 with backlighting technique between the polarizer 1 and the analyzer (polarizer 2). In (b), there is a picture of the circular Ferrocell used to simulate jumping sun dogs in setup 2.
We have used neodymium (Ne-Fe-B) magnets placed at some distance of the Ferrocell in order to change the light patterns. For example, the value magnetic field of a cylindrical magnet was obtained with a Lakeshore gaussmeter model 475 DSP at room temperature of 27˚C in the plots is shown in Figure 3. Changing the position of the magnets, we can modify the magnetic field in each Ferrocell, and consequently change the structure of the magnetic nanoparticles.
3. Polarized Light and Ferrocell
Before getting into the jumping sun dog simulation using laser dogs, let us explain some features of the optical properties of the Ferrocell in the presence of the magnetic field, in order to understand how to control the nanoparticles with an external magnetic
Figure 3. Using the gaussmeter, we have obtained the values of the magnetic field of a cylindrical magnet with the distance for two distinct configurations. In (a) the magnetic field of pole configuration with the distance r, and in (b) the dipole configuration with the distance l. Each dashed line is a curve fitting that has the best fit to the experimental data, and they are explained in Section 3.
field. Basically, the magnetic nanoparticles arrange themselves in complex geometries in ferrofluids, such as labyrinth or needles, due to the long range dipolar interactions. One way to observe these complex geometries is using polarized light.
Polarization measurements show that the static magnetic field can alter the structure of the nanoparticles inside the Ferrocell, changing the light polarization, as it is shown in Figure 4. We can see the main effect of a cylindrical magnet placed at the center of the Ferrocell, with the magnetic pole facing the Ferrocell in Figure 4(a).
There are black fringes and bright regions, creating a pattern resembling a cross. The outstanding feature of this pattern is its stability. For example, in Figure 4(e), Figure 4(f) we have used a cubic magnet in the pole configuration, and we have observed a similar pattern of light polarization, like the pattern observed for the cylindrical magnet of Figure 4(a). Changing the position of the magnet, the pattern remains as a dark cross with four bright lobes, centered at the magnet. These patterns are strong evidence that the Ferrocell acts as one diffraction grating in the presence of the magnetic field.
The basic explanation for this behavior is that the ferrofluid is a complex fluid, changing its structure for different values of applied magnetic field. Other structures were observed in ferrofluids, and these structures were reported in the literature more than a decade ago [9] .
In a more technical way, these patterns of light polarization represent the Faraday effect in light transmission geometry. For the same value of the magnetic field, there are different values of light intensity in different points of the Ferrocell, indicating some sort of interaction between the structures of the ferrofluid. For example, in Figure 4(b), we can observe the quantitative aspect of light amplitude of a circular stripe chosen around the magnet placed at the center of the Ferrocell1 using the pole configuration. The rotation polarization is periodic inside this circular stripe, and Figure 4(c) shows the diagram of light amplitude. The plot of Figure 4(d) represents the light amplitude for different angle values, ranging from −90˚ to 90˚, projected in y axis.
Using the information obtained from these patterns, we can explain the observed data with a phenomenological model. In order to obtain this model, we need to know the mathematical expression of the external magnetic field created by the magnet, and the equation representing needlelike structure. First, the calculation of the exact magnetic field of the magnet at any point in space has some mathematical complexities and involves the properties of the magnetic materials. Things are simpler using direct measures of the magnetic field discussed in the previous section, such as the equation obtained for the horizontal component of the magnetic field Bhor of a magnet in the pole configuration of Figure 3(a), which is given by:
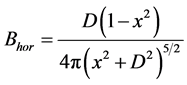 , (1)
, (1)
and for the case of dipole configuration of Figure 3(b):
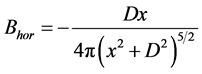 , (2)
, (2)
Figure 4. Optical properties of the Ferrocell subjected to a magnetic field, with a magnetic pole facing the Ferrocell. In (a), the image of the light pattern obtained from the Faraday effect in the transmission geometry of the Ferrocell with a cylindrical magnet placed in the middle of the Ferrocell. In (b), the plot of the light amplitude of the circular stripe in (a) was chosen in order to show the different values of the light intensity. The diagram of the light intensity of the circular stripe in (c). In (d), light amplitude from −90˚ to 90˚ showing the rotation polarization of the ferrocell, and it gives a hint of how the Ferrocell can interact with light for the same intensity of magnetic field for different positions. We have observed that this pattern is centered in the pole of the magnet (e), and the isoclines remain aligned with the axis of the cell, if the magnet is placed in a different position (f).
where D is a constant featured for this magnet and x is the distance from the center of the magnet to the tip of the magnetic field sensor, based on the diagrams in the plots of Figure 3.
Second, the formation of the needlelike structures of Figure 5 is directed related with the magnetic field B around 200 G, and for the case of the circular stripe of Figure 4(a), Figure 4(b) obtained from the experiment, the direction of the polarization of the needles inside the circular region, with radius R and width a, is given by the coordinates (xi, yi) and (xi+1, yi+1) for the angle θ:
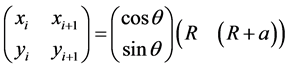 (3)
(3)
The neddles are oriented from R to R + a direction, and we have observed from the experiment that the light intensity has the maximum intensity for θ values equal 45˚, 135˚, 225˚, and 315˚. In addition to this, the pattern is black placing a cylindrical magnet in the pole configuration in the Ferrocell1 for θ values equal 0˚, 90˚, 180˚, and 270˚, because for these angle values the ferrofluid needles are aligned with one of the two polarizers.
With Equations (1)-(3), we can derive the equation for light intensity through the system formed by the first polarizer, Ferrocell, and the second polarizer. The first and last polarizers are oriented at 90˚ with respect to each other, the Ferrocell has its polarization
Figure 5. Comparisons between light patterns and simulations using polarized light with the Ferrocell. In (a) the cubic magnet placed at pole configuration in the middle of the Ferrocell, and the simulation is presented in (b). The experiment in (c), for the case of the magnet in the dipole configuration, and in (d) the simulation of the light intensity through the Ferrocell in the dipole configuration.
aligned with the angle θ, with the needles shaped by the magnetic field given by Equation (1). Therefore the second polarizer is rotated an angle (π/2 − θ) from the Ferrocell. Considering the intensity after passing the first polarizer is I1, the intensity after passing the Ferrocell is I2, is given by:
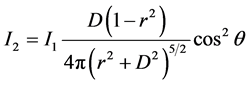 . (4)
. (4)
The intensity after the second polarizer for each point with coordinates (r, θ), I3, is given by:
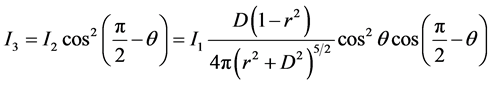 , (5)
, (5)
and rearranging the terms of Equation (5), the intensity after the second polarizer is:
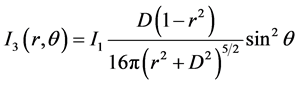
 . (6)
. (6)
where r ranges from 0 to infinity, and θ ranges from 0˚ to 360˚.
Based on this model, we can simulate the light intensity for different configurations of external magnetic fields, as it is shown in Figure 5. This analysis is a very good way to understand the role of ferrofluid needles interacting with light, and we can extrapolate that a system with ice crystals with same size, oriented by an external electric field could have similar effect in the light scattering. To sum up, we can see that a static magnetic field placed near the Ferrocell creates a structure inside the Ferrocell, which can be mapped with polarized map. In the next section we will explore some aspects of the light scattering in this structure.
4. The Jumping Laser Dogs
Performing some experiments [7] and obtaining similar light patterns to those observed in the atmospheric optics, we consider that it is important to note that the parhelic circle is an effect combining the properties of the geometric optics and wave optics at same time, involving the concept of diffracted ray [8] . In this way, the parhelic circle was explained in our previous papers [7] [8] as the manifestation of diffracted rays, as it is shown in Figure 6 and, according to GTD, when a light beam hits a needlelike structure of ice crystals obliquely, there is a cone of diffracted rays and the cross section of this cone is given by:
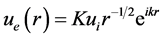 (7)
(7)
where K is the diffraction coefficient, ui is the incident field, and r is the distance between the ferrofluid and the screen, and k = 2π/λ is the wave number of the incident field with wavelength λ. This is similar to the case when the laser beam hits curved prisms and creates laser dogs [10] . Using the diagram of Figure 6(a), the z coordinate of the ferrofluid needle coordinate system (z, r, θ) coincides with the needle axis. The
Figure 6. The diagram of the laser scattering with the parlaseric circle with the laser dog pattern with nanoparticles forming a needle in (a). In (b), the laser spot and the laser dog with B = 0 gauss, and in (c) the parlaseric circle for B = 600 gauss.
plane θ = 0 contains the incident beam. The angle ϕ defines the tilt between the perpendicular to the direction of the propagation of the incident beam and the needle. The light scattered emerges along the surface of the cone with apical angle 180˚ - 2ϕ and is viewed on the circle ue, sighting towards the apex of the cone.
The same effect occurs when light hits the needlelike formation in ferrofluids [11] . We can observe this type of diffracted rays for a setup without any polarizer, as it is shown in Figure 6. Part of the green laser is passing through the Ferrocell forming a laser spot at right side of this picture, and part of light is reflected forming the laser dog at left side. Applying the magnetic field in the Ferrocell used in setup 2 induces the creation of diffracted rays, represented by the curved lines of Figure 6(c) for 600 gauss, because the colloidal system of ferrofluids undergoes structural changes under external field leading to linear chains [9] , as it was discussed in the previous section.
Our simulation of jumping sundogs is shown in Figure 7. Basically, the laser beam is scattered by the needlelike structure in the Ferrocell (setup 2), while the magnetic field is displaced. The optical patterns observed for micron sized needles are a simultaneous manifestation of both scattering and diffraction. In order to measure the displacement of the diffracted rays obtained with the Ferrocell, the same laser beam was diffracted by a vertical soap film, forming a light pattern of a horizontal well defined dashed line. In Figure 7(a), for the magnetic field of B = 900 gauss, we have obtained a vertical diffracted ray, forming the simulation of the sun dog. Changing the orientation of the magnetic field, we can observe the motion of the sun dog in comparison to the horizontal dashed line. The motion of these patterns represents the jumping laser dogs, which are controlled by the motion of the external magnetic field.
Figure 7. The jumping laser dog dynamics for different orientations of the needlelike particles, changing the external magnetic field. Using the fixed light diffraction of a soap film as the reference, we have measure the following angles between the laser dog and the reference: (a) 90˚, (b) 120˚, (c) 135˚, (d) 180˚, (e) 225˚, and in (f) the laser dog is rotated 245˚.
We can observe that the light streak related to the jumping laser dog is different from that produced by the soap film. First, the laser dog can be controlled by the magnetic field, and second the absence of well defined spacing between fringes from multiple microscope particles, such as ice crystals or nanoparticles. According some authors, the absence of fringe pattern in ferrofluid is an integral sum of diffraction events from individual chains, and the observed pattern can be interpreted as a result of the combination of multiple diffraction. Considering that the scale of the ice crystals present in clouds are around hundreds of micrometers, it is plausible to think that the same type of light scattering is present in the systems composed by ferrofluid or ice crystal, and some computational approaches [12] use a mix of geometric optics and Fraunhofer diffraction to calculate the scattering of light by ice crystals present in clouds.
5. Conclusions
Using some simple concepts described in the geometrical theory of diffraction, we have obtained the jumping laser dogs with the motion of an external magnetic field, observing the patterns created by diffracted rays in the Ferrocell system. In this way, we have tested the hypothesis that particles with the same size of ice crystals in a thundercloud could be reoriented by an external field, scattering the light differently. Like most disciplines involving natural phenomena, the study of atmospheric optics utilizes many branches of physics. The deeper one tries to understand them, the more soft matter physics, optics, ice crystals thermodynamics and other facets are required. In this paper, we have proposed an experiment in which a complex fluid subjected to external field scatters the light forming jumping laser dog, a phenomenon analogous to the jumping sun dogs. Using polarized light, we have observed how the magnetic nanoparticles arrange themselves in complex geometries in ferrofluids, such as needles, due to the long range dipolar interactions.
In our analogy, the ice crystals are represented by the needlelike structures of ferrofluid, and electric fields are represented by magnetic fields. For certain conditions of the wavelengths and sizes of these light scatterers, the angles of reflection and refraction are not defined by the angle of incidence, and part of the incoming light striking the scatterer will give rise to a conical shell of diffracted rays, forming halos or partial halos. Using this comparison, we have inferred that the atmosphere could be associated with a complex fluid, in which a mixture of solid (ice crystals) and gas (air) exhibits unusual responses to applied electric field, creating jumping sun dogs or crown flashes.
Acknowledgements
This work was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Instituto Nacional de Ciência e Tecnologia de Fluidos Complexos (INCT-FCx) and Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), FAPESP/CNPq #573560/2008-0.
Cite this paper
Tufaile, A., Vanderelli, T.A. and Tufaile, A.P.B. (2016) Observing the Jumping Laser Dogs. Journal of Applied Mathematics and Physics, 4, 1977-1988. http://dx.doi.org/10.4236/jamp.2016.411198
References
- 1. Plait, P. (2011) Discover Magazine Blog.
http://blogs.discovermagazine.com/badastronomy/2011/10/25/amazing-video-of-a-bizarre-twisting-dancing-cloud/#.V36ZzNIrJdh - 2. Tufaile, A.P.B., Vanderelli, T., Amorim, R. and Tufaile, A. (2016) Simulating the Jumping Sun Dogs. Proceedings of 12th Conference on Light and Color in Nature, Granada, 31 May-3 June 2016, 24-25.
https://drive.google.com/drive/folders/0BxhJRGXxaO-FUURIcnpIdEU4QjA - 3. Foster, T.C. and Hallett, J. (2008) Enhanced Alignment of Plate Ice Crystals in a Non-Uniform Electric Field. Atmospheric Research, 90, 41-53.
http://dx.doi.org/10.1016/j.atmosres.2008.02.017 - 4. Vonnegut, B. (1965) Orientation of Ice Crystals in the Electric Field of a Thunderstorm. Weather, 20, 310-312.
http://dx.doi.org/10.1002/j.1477-8696.1965.tb02740.x - 5. Koop, T. (2013) Rare but Active. Nature, 498, 302.
http://dx.doi.org/10.1038/nature12256 - 6. Keller, J.B. (1962) Geometrical Optics Theory of Diffraction. Journal of the Optical Society of America, 52, 116-130.
http://dx.doi.org/10.1364/JOSA.52.000116 - 7. Tufaile, A. and Tufaile, A.P.B. (2015) Parhelic-Like Circle from Light Scattering in Plateau Borders. Physics Letters A, 379, 529-534.
http://dx.doi.org/10.1016/j.physleta.2014.12.006 - 8. Tufaile, A. and Tufaile, A.P.B. (2015) The Dynamics of Diffracted Rays in Foams. Physics Letters A, 379, 3059-3068.
http://dx.doi.org/10.1016/j.physleta.2015.10.011 - 9. Islam, M.F., Lin, K.H., Lacoste, D., Lubensky, T.C. and Yodt, A.G. (2003) Field-Induced Structures in Miscible Ferrofluids Suspensions with and without Latex Spheres. Physical Review E, 67, 021402.
http://dx.doi.org/10.1103/PhysRevE.67.021402 - 10. Conover, E. (2015) Researchers Create “Laser Dogs” with Soap Bubbles. Science.
http://dx.doi.org/10.1126/science.aaa7816 - 11. Laskar, J.M., Brojabasi, S., Raj, B. and Philip, J. (2012) Comparison of Light Scattering from Self Assembled Array of Nanoparticle Chains Cylinders. Optics Communications, 285, 1242-1247.
http://dx.doi.org/10.1016/j.optcom.2011.11.103 - 12. Bi, L., Yang, P., Kattawar, G.W., Hu, Y. and Baum, B.A. (2011) Scattering and Absorption of Light by Ice Crystals: Solution by a New Physical-Geometric Optics Hybrid Method. Journal of Quantitative Spectroscopy & Radiative Transfer, 112, 1492-1508.
http://dx.doi.org/10.1016/j.jqsrt.2011.02.015








