Journal of Applied Mathematics and Physics
Vol.04 No.06(2016), Article ID:67145,9 pages
10.4236/jamp.2016.46105
On the Stringy Ghosts Which We Call the Missing Dark Energy of the Cosmos
Mohamed S. El Naschie
Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 May 2016; accepted 4 June 2016; published 7 June 2016
ABSTRACT
Dark energy is explained using familiar notions and concepts used in quantum field theory, string theory and the exact mathematical theory of spacetime. The main result of the present work is first a new mathematical definition of pre-quantum spacetime (QST) as a multiset made of infinitely many empty Cantor sets connected to pre-quantum wave empty set (QW) and the pre-quan- tum particle (QP) zero set via the cobordism equation ∂(QW) = (QP)U(QST). Second, and in turn, this new path of reasoning is used to validate the quantum splitting of Einstein’s E = mc2 into the sum of the ordinary energy E = mc2/22 of the quantum particle and the dark energy E = mc2(21/22) of the quantum wave, used predominantly to explain the observed accelerated expansion of the universe.
Keywords:
Quantum Spacetime, Quantum Ghost States, Dark Energy, Spacetime Cobordism, E-Infinity Theory, Fractal-Cantorian Spacetime, Noncommutative Geometry, ‘t Hooft-Susskind Holography

1. Introduction and Motivation
The theme of the present scientific essay is aptly captured by a remark ascribed to Wolfgang E. Pauli “God made the bulk but the surface was invented by the devil” [1] . It is evident that when the scale tends to an extremely small quantum and fractal scale [1] - [7] , then the surface to volume ratio grows extremely large and the boundary effect dominates over the volume effect and consequently almost all of latent “space” energy is found located at the boundary [1] [2] . In anticipation of the main result of the present work, we can say that what is called dark energy [8] - [29] is closely related to this boundary energy but with a twist. Suppose now the universe is a single random version of the classical triadic Cantor set [3] - [6] . Given this theoretical toy model then at the limit when we have only Cantor set points separated by “nothing” as their “boundary”, almost all the energy will be located in this “nothing” because this nothing is the surface of the vanishing Cantor “dust” [7] - [31] . What we just explained could be paraphrased in various equivalent languages and corresponding mental pictures. For instance we know that the unit interval is the simplest example of a cobordism [32] - [38] . Consequently by constructing a random triadic Cantor set on and in this interval we have de facto advanced a cobordism spacetime theory in one dimension harbouring two sets [8] - [17] . The first will be a substance like Cantor dust with a Hausdorff dimension equal to  and zero topological dimension [8] - [32] . This will be shown later to give rise to the pre-quantum particles and the associated ordinary energy. The second set is a spacetime-like non-substance fat Cantor set with a Hausdorff dimension
and zero topological dimension [8] - [32] . This will be shown later to give rise to the pre-quantum particles and the associated ordinary energy. The second set is a spacetime-like non-substance fat Cantor set with a Hausdorff dimension 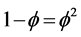 and a topological dimension minus one (−1) indicating that it is essentially an empty set [7] - [9] . This will be shown later to give rise to the quantum wave which harbours what has been dubbed the missing dark energy of the cosmos [9] - [29] . From the preceding description even a reader with no advanced mathematical knowledge in topology and cobordism theory has probably got the right mental picture already, namely that the quantum wave empty set is the “border” or surface of the quantum particle zero set [7] [8] . One step is still missing to come to the quantitative result that confirms what is transpiring from the preceding toy model of our universe, namely that the “boundary” energy is nothing but the energy of the quantum wave and that is in fact what we call dark energy. This step is the following realization gained from the cobordism theory of spacetime [33] which simply put, means that Einstein’s D = 4 spacetime is cobodent to Kaluza-Klein spacetime D = 5. Remembering that for a simple two-dimensional square area A is multiplicative A = a2 while the length of the four border lines L is additive L = 4a then generalizing to five dimensions we find that the quantum particle quasi volume must be f5 while the quantum wave quasi volume must be 5f2 [8] - [31] .
and a topological dimension minus one (−1) indicating that it is essentially an empty set [7] - [9] . This will be shown later to give rise to the quantum wave which harbours what has been dubbed the missing dark energy of the cosmos [9] - [29] . From the preceding description even a reader with no advanced mathematical knowledge in topology and cobordism theory has probably got the right mental picture already, namely that the quantum wave empty set is the “border” or surface of the quantum particle zero set [7] [8] . One step is still missing to come to the quantitative result that confirms what is transpiring from the preceding toy model of our universe, namely that the “boundary” energy is nothing but the energy of the quantum wave and that is in fact what we call dark energy. This step is the following realization gained from the cobordism theory of spacetime [33] which simply put, means that Einstein’s D = 4 spacetime is cobodent to Kaluza-Klein spacetime D = 5. Remembering that for a simple two-dimensional square area A is multiplicative A = a2 while the length of the four border lines L is additive L = 4a then generalizing to five dimensions we find that the quantum particle quasi volume must be f5 while the quantum wave quasi volume must be 5f2 [8] - [31] .
In the present work we will give the details leading to a conclusion based on the above that the ordinary energy density of the cosmos is given by 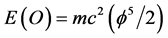 while the dark energy density is simply the compliment of E(O) and is given by
while the dark energy density is simply the compliment of E(O) and is given by 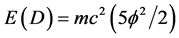 [8] - [31] . Furthermore we show that this is actually a consequence of the measure concentration theorem of Dvoretzky and may be explained within conventional quantum field theory via string theory as being a consequence of ad hoc states referred to as zero norms and ghost states without realizing the pure mathematical origins of these states as explained here [28] - [32] which leads to the dissection of Einstein’s E = mc2 to
[8] - [31] . Furthermore we show that this is actually a consequence of the measure concentration theorem of Dvoretzky and may be explained within conventional quantum field theory via string theory as being a consequence of ad hoc states referred to as zero norms and ghost states without realizing the pure mathematical origins of these states as explained here [28] - [32] which leads to the dissection of Einstein’s E = mc2 to 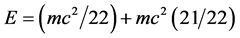 where
where 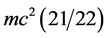 is the 95.5% dark energy density of the cosmos. We were faced in the present work with the usual problem of wanting to make the work self contained while keeping the length of the paper as short as possible. That dilemma was solved as usual by including a large number of references [1] - [99] .
is the 95.5% dark energy density of the cosmos. We were faced in the present work with the usual problem of wanting to make the work self contained while keeping the length of the paper as short as possible. That dilemma was solved as usual by including a large number of references [1] - [99] .
2. An Ionescoian Scene from the Absurd Scientific Theatre of Reality
Waiter! There is a ghost in my soup. You see 95.5 percent of all the spoons I take to my mouth from this circular soup bowl you brought me turns out to be empty as soon as it reaches my mouth. No matter how hard I try, there is simply no soup in my spoon. It is both ridiculous and incredible. I counted accurately and only 4.5 percent of the spoons had soup in them which I could see, feels its temperature and taste. Yes of course there is the possibility that the soup bowl is empty, I mean almost empty because the capillary forces of the boundary of the bowl are attracting the soup there, leaving only 4.5% of the soup in the middle and that what my spoon is taking into my mouth… however this seems also ridiculous because there is no space to harbour at the boundary 95.5 percent of the soup… oh yes and on reflection there is again the possibility of a hyperbolic soup bowl so that the boundary is really far away at infinity and we have infinite hidden space where the 95.5 percent soup could be comfortably hiding at the finite infinity…
There is no doubt this absurd dialogue or more accurately internal monologue reminiscent of the writings of Eugene Ionesco or Samuel Beckett could not have taken place in an Italian or any other restaurant but in all earnest something similar has taken place and is still vividly discussed in cutting edge scientific research in quantum cosmology in connection with the question of the missing dark energy density of the cosmos [10] - [21] .
The present short paper is intended to shed a relatively new light on the subject of the “mystery” of the “missing” dark energy. We will try to convey these advanced cutting edge scientific research results with a minimum of technical jargon and whenever this is unavoidable, we will attempt to explain these terms in a down to earth manner. Now that is nothing new and in fact it is the standard way when explaining a difficult subject to a wider scientifically educated but not specialized reader. However in the present context this issue of the language used is almost the crux of the matter. In a nutshell, the problem is that while Google translation with all its weaknesses has made a plethora of different languages accessible to almost all inhabitants of planet earth, something similar for science is still lacking. The scientific community is largely divided by private languages. To be more specific and to the point, the mystery of dark energy is in our opinion, no mystery if we accept as we do here that negative probabilities, phantoms, negative norms and ghosts as those familiar from quantum chromo dynamics as well as the empty set of the Menger-Urysohn dimensional theory means more or less the same thing and are what makes dark energy be called dark. This is our starting point and almost also our conclusion and end point. The rest of this article will be devoted to explaining in more detail what we have just said in considerable economy of thoughts.
3. The Fat Cantor Ghosts as Dark Energy
In describing a Cantor set, that is a zero length measure clopen interval, which is to say a simultaneously open and closed unit interval that possesses a positive value dimension (fractal-Hausdorff dimension), the word ghost crosses the mind and was in fact used by the author on numerous previous occasions [56] . How else could we describe something which has a length equal zero so that it is physically not in our “world” and yet has a substantial dimension, albeit Hausdorff dimension amounting to 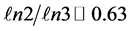 for a deterministic Cantor set and
for a deterministic Cantor set and 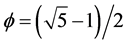 = 0.618033989 for a randomly constructed triadic Cantor set which means it is somehow connected to our world. At the time we encountered this mysterious and paradoxical nature of a Cantor set and utilized it for problems in quantum physics and relativity theory, we were not aware that this same term was in fact already in use for certain fundamental questions central to quantum field theory and in particular to string quantization and QCD [32] . The word ghost is used there to refer to norms which on its face value should not be part of “reality”, ergo it should not be part of the “physical” Hilbert space. However these norms are there and not there for logical-mathematical reasons. This paradoxical situation was then helped by developing mathematical manoeuvres to have one’s cake and get rid of it simultaneously [85] - [94] . In this respect the situation is rather reminiscent of our Cantor set and far more to the surface of a Cantor set which is a second even more puzzling Cantor set possessing a non-zero measure on the one side and a negative topological dimension, a so called Menger-Urysohn dimension on the other side. Such sets are well known in set theory and the theory of dimensions under the name of “empty” set. It took some time for the author to realize the obvious although, or maybe because it is very obvious to see at once. The language of the zero and empty set used by the author in his E-infinity theory is a pure mathematical tautology of the theory of zero and negative ghosts of Nambu-Gotto strings and its Gulpta-Bleuler quantization. By analogy to our previous result it becomes clear that ghosts are the origin of dark energy and that the rough density ratio rooted in the critical dimensions D1 = 26 and D2 = 25 may be found from the reduced dimensions [8] - [32]
= 0.618033989 for a randomly constructed triadic Cantor set which means it is somehow connected to our world. At the time we encountered this mysterious and paradoxical nature of a Cantor set and utilized it for problems in quantum physics and relativity theory, we were not aware that this same term was in fact already in use for certain fundamental questions central to quantum field theory and in particular to string quantization and QCD [32] . The word ghost is used there to refer to norms which on its face value should not be part of “reality”, ergo it should not be part of the “physical” Hilbert space. However these norms are there and not there for logical-mathematical reasons. This paradoxical situation was then helped by developing mathematical manoeuvres to have one’s cake and get rid of it simultaneously [85] - [94] . In this respect the situation is rather reminiscent of our Cantor set and far more to the surface of a Cantor set which is a second even more puzzling Cantor set possessing a non-zero measure on the one side and a negative topological dimension, a so called Menger-Urysohn dimension on the other side. Such sets are well known in set theory and the theory of dimensions under the name of “empty” set. It took some time for the author to realize the obvious although, or maybe because it is very obvious to see at once. The language of the zero and empty set used by the author in his E-infinity theory is a pure mathematical tautology of the theory of zero and negative ghosts of Nambu-Gotto strings and its Gulpta-Bleuler quantization. By analogy to our previous result it becomes clear that ghosts are the origin of dark energy and that the rough density ratio rooted in the critical dimensions D1 = 26 and D2 = 25 may be found from the reduced dimensions [8] - [32]
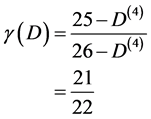 (1)
(1)
or alternatively
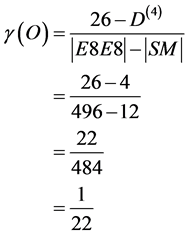 (2)
(2)
so that we have again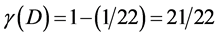 . Assuming E = mc2 to be not merely the maximal energy convergence possible but logically as well as intuitively the maximal average energy density of the universe we see that
. Assuming E = mc2 to be not merely the maximal energy convergence possible but logically as well as intuitively the maximal average energy density of the universe we see that 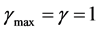 while
while 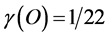 and
and 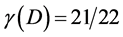 would imply that E(O) = mc2/22 and E(D) = mc2(21/22) which is in hard to believe accuracy agreement with the overwhelming actual cosmic measurements, particularly COBE, WMAP and Type 1a supernova as well as Hubble and Plank projects [8] - [22] .
would imply that E(O) = mc2/22 and E(D) = mc2(21/22) which is in hard to believe accuracy agreement with the overwhelming actual cosmic measurements, particularly COBE, WMAP and Type 1a supernova as well as Hubble and Plank projects [8] - [22] .
4. Phantom in Hyperspace
Phantoms are supposed to be much stronger driving forces for cosmic expansion than the quintessence generalization of Einstein’s cosmological constant. It is essentially negative energy and as such a radical proposal with no parallel in mainstream physics except other radical and related proposals such as negative gravity and the like. However if we pause for a second and ponder the quantum wave as viewed by E-infinity theory [8] - [29] , then we realize that it is modelled by the empty set which is phantom enough in addition to being physically there via the Hausdorff dimension of the empty set 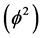 and moreover it has its ties with the negative domain because the empty set, ergo the wave has the remarkable topological dimension minus one so that the combined von
and moreover it has its ties with the negative domain because the empty set, ergo the wave has the remarkable topological dimension minus one so that the combined von
Neumann-Connes extended dimension reads 
tion or equivalently using the bijection formula 

5. Almost Pitfall Free Approach
Now that we are coming to the end of the present work, a few words on the pitfalls and possible confusion are in order at this point. There are many different notions of ghosts in physics. There are for instance good ghosts and consequently bad ghosts. The archetypical good ghost is the Faddeev-Popov ghost. By contrast negative norms are considered bad ghosts. In addition there are subtle exceptions such as the ghosts associated with the Feynman-‘t Hooft gauge theory and the mass of the Higgs. There are anti-commuting ghosts and ghost field Lagrangian [90] . All these more or less special cases and ad hoc techniques may easily be avoided by realizing the unifiying nature of the present proposal of defining the quantum wave as the empty set and that the corresponding energy is a negative one which was long dubbed dark energy while not knowing that it is the same thing as the energy of the quantum wave. In view of the above the reader can appreciate the benefit of the clarity of using the sharp terms of the language of pure mathematics [8] .
6. Renormalization, Fractal Spacetime and Dark Energy
Before ending our analysis, there is one more vital point left which is quite central to understanding the present approach. The essence of this point is the basic equivalence between the move from the energy level of electricity, magnetism and the weak force to that of the electroweak unification or more generally, all higher energy scales connected to electro chromodynamics and GUT and phase transition. Accepting this view we see that such energy scale transition corresponds to phase space transition expressed in a transition from smooth D = 4 classical and special relativistic spacetime to a first stage Cantorian-fractal spacetime dimensionality. This important dimensional transmutation is deeply linked to ‘t Hooft’s dimensional regularization in its various forms used by G. ‘t Hooft [91] [98] , M. Veltman and K. Wilson and characterized by 




in full agreement with cosmic measurements of COBE, WMAP and Type 1a supernova [7] - [12] .
7. Discussion
Set theory in general and notions like the zero and empty set in particular [8] - [31] [39] - [55] is not part of the traditional mathematical training of physics. For such and other historical reasons when facing deep and foundational problems in quantum physics and quantum cosmology, research in these fields had naturally the needed ingenuity to reinvent the mathematical theory needed but this happened of course using different names and jargon [85] - [91] . As harmless as this may be, it did cause some confusion as documented in the present work where it became evident that dark energy did not come out of the blue. That way we discovered that we do not need to add any new notion to understand dark energy and instead we found that we are basically talking about the same things using different names and sometimes different languages ranging from that of pure mathematics and set theory to that of modern quantum field theory and the negative norms and ghosts of superstrings. The author is reminded in this context of what Ludwig Wittgenstein wrote in his Tractatus Logico-Philosphicus under paragraph No. 4.0031 “All philosophy is a ‘critique of language’.” We just need here to change the words philosophy to natural philosophy and language to mathematics in the proposition of Wittgenstein to make it of universal validity in theoretical and mathematical physics [95] .
8. Conclusions
In the present work we made some important insights into the nature of space, time and energy:
1) The zero set may be regarded as the quintessence of the quantum particle.
2) The empty set is the quintessence of the quantum wave.
3) Spacetime is a multi-set (multi-fractal) made of infinitely many empty sets with increasing degrees of emptiness.
4) The zero set quantum particle and the multi-set spacetime are cobordant via the empty set quantum wave. These pure mathematical objects correspond to negative norms and ghosts of string theory.
5) The relation between the quantum wave, the quantum particle and the spacetime manifolds could be roughly expressed symbolically in the following notation of the theory of cobordism [33] - [38]
where QW is the quantum wave, QP is the quantum particle and ST is spacetime [8] [32] .
6) Einstein’s 



Cite this paper
Mohamed S. El Naschie, (2016) On the Stringy Ghosts Which We Call the Missing Dark Energy of the Cosmos. Journal of Applied Mathematics and Physics,04,979-987. doi: 10.4236/jamp.2016.46105
References
- 1. Zangwill, A. (1988) Physics at Surfaces. Cambridge University Press, Cambridge, UK.
http://dx.doi.org/10.1017/CBO9780511622564 - 2. Pheifer, P. and Avnir, D. (1983) Chemistry in Noninteger Dimensions between Two and Three. I. Fractal Theory of Heterogeneous Surfaces. The Journal of Chemical Physics, 79, 3558.
http://dx.doi.org/10.1063/1.446210 - 3. Addison, P.S. (1997) Fractals and Chaos: An Illustrated Course. IOP, Bristol.
- 4. Avef, H. and El Naschie, M.S. (1995) Chaos Applied to Fluid Mixing. Pergamon-Elsevier, Oxford, UK.
- 5. Kapitaniak, T., Ed. (1992) Chaotic Oscillators (Theory and Applications). World Scientific, Singapore.
http://dx.doi.org/10.1142/9789814360258 - 6. Moon, F. (1992) Chaotic and Fractal Dynamics. John Wiley, New York, USA.
http://dx.doi.org/10.1002/9783527617500 - 7. El Naschie, M.S. (2016) Einstein’s Dark Energy via Similarity Equivalence, ‘t Hooft Dimensional Regularization and Lie Symmetry Groups. International Journal of Astronomy & Astrophysics, 6, 56-81.
http://dx.doi.org/10.4236/ijaa.2016.61005 - 8. El Naschie, M.S. (2015) An Exact Mathematical Picture of Quantum Spacetime. Advances in Pure Mathematics, 5, 560-570.
http://dx.doi.org/10.4236/apm.2015.59052 - 9. El Naschie, M.S. (2015) If Quantum “Wave” of the Universe Then Quantum “Particle” of the Universe: A Resolution of the Dark Energy Question and the Black Hole Information Paradox. International Journal of Astronomy & Astrophysics, 5, 243-247.
http://dx.doi.org/10.4236/ijaa.2015.54027 - 10. El Naschie, M.S. (2015) On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Science, 5, 313-324.
http://dx.doi.org/10.4236/ojapps.2015.57032 - 11. El Naschie, M.S. (2015) From Fusion Algebra to Cold Fusion or from Pure Reason to Pragmatism. Open Journal of Philosophy, 5, 319-326.
http://dx.doi.org/10.4236/ojpp.2015.56040 - 12. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 13. El Naschie, M.S. (2016) From Witten’s 462 Supercharges of 5-D Branes in Eleven Dimensions to the 95.5 Percent Cosmic Dark Energy Density Behind the Accelerated Expansion of the Universe. Journal of Quantum Information Science, 6, 57-61.
http://dx.doi.org/10.4236/jqis.2016.62007 - 14. El Naschie, M.S. (2016) Negative Norms in Quantized Strings as Dark Energy Density of the Cosmos. World Journal of Condensed Matter Physics, 6, 63-67.
http://dx.doi.org/10.4236/wjcmp.2016.62009 - 15. El Naschie, M.S. (2016) On a Quantum Gravity Fractal Spacetime Equation: QRG HD + FG and Its Application to Dark Energy—Accelerated Cosmic Expansion. Journal of Modern Physics, 7, 729-736.
http://dx.doi.org/10.4236/jmp.2016.78069 - 16. El Naschie, M.S. (2016) Einstein-Rosen Bridge (ER), Einstein-Podolski-Rosen Experiment (EPR) and Zero Measure Rindler KAM Cantorian Spacetime Geometry (ZMG) Are Conceptually Equivalent. Journal of Quantum Information Science, 6, 1-9.
http://dx.doi.org/10.4236/jqis.2016.61001 - 17. El Naschie, M.S. (2015) Dark Energy and Its Cosmic Density from Einstein’s Relativity and Gauge Fields Renormalization Leading to the Possibility of a New ‘t Hooft Quasi Particle. The Open Journal of Astronomy, 8, 1-17.
http://dx.doi.org/10.2174/1874381101508010001 - 18. El Naschie, M.S. (2016) Quantum Dark Energy from the Hyperbolic Transfinite Cantorian Geometry of the Cosmos. Natural Science, 8, 152-159.
http://dx.doi.org/10.4236/ns.2016.83018 - 19. El Naschie, M.S. (2015) Hubble Scale Dark Energy Meets Nano Scale Casimir Energy and the Rational of Their T-Duality and Mirror Symmetry Equivalence. World Journal of Nano Science and Engineering, 5, 57-67.
http://dx.doi.org/10.4236/wjnse.2015.53008 - 20. El Naschie, M.S. (2014) Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91.
http://dx.doi.org/10.4236/jqis.2014.42008 - 21. El Naschie, M.S. (2015) Application of Dvoretzky’s Theorem of Measure Concentration in Physics and Cosmology. Open Journal of Microphysics, 5, 11-15.
http://dx.doi.org/10.4236/ojm.2015.52002 - 22. El Naschie, M.S. (2015) A Resolution of the Black Hole Information Paradox via Transfinite Set Theory. World Journal of Condensed Matter Physics, 5, 249-260.
http://dx.doi.org/10.4236/wjcmp.2015.54026 - 23. El Naschie, M.S. (2015) The Counterintuitive Increase of Information Due to Extra Spacetime Dimensions of a Black Hole and Dvoretzky’s Theorem. Natural Science, 7, 483-487.
http://dx.doi.org/10.4236/ns.2015.710049 - 24. El Naschie, M.S. (2014) Entanglement of E8E8 Exceptional Lie Symmetry Group Dark Energy, Einstein’s Maximal Total Energy and the Hartle-Hawking No Boundary Proposal as the Explanation for Dark Energy World. Journal of Condensed Matter Physics, 4, 74-77.
- 25. Marek-Crnjac, L. (2015) On El Naschie’s Fractal-Cantorian Space-Time and Dark Energy—A Tutorial Review. Natural Science, 7, 581-598.
http://dx.doi.org/10.4236/ns.2015.713058 - 26. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.
http://dx.doi.org/10.1134/S0202289313030031 - 27. El Naschie, M.S. (2016) Cosserat-Cartan and de Sitter-Witten Spacetime Setting for Dark Energy. Quantum Matter, 5, 1-4.
http://dx.doi.org/10.1166/qm.2016.1247 - 28. El Naschie, M.S. (2015) The Self Referential Pointless Universe Geometry as the Key to the Resolution of the Black Hole Information Paradox. International Journal of Innovation in Science and Mathematics, 3, 254-265.
- 29. El Naschie, M.S. (2016) On a Fractal Version of Witten’s M-Theory. Journal of Astronomy & Astrophysics, 6, 135-144.
http://dx.doi.org/10.4236/ijaa.2016.62011 - 30. Connes, A. (1994) Noncommutatie Geometry. Academic Press, San Diego, USA. (See in particular pages 85-93)
- 31. Marek-Crnjac, L. (2011) The Hausdorff Dimension of the Penrose Universe. Physics Research International, 2011, Article ID: 874302.
http://dx.doi.org/10.1155/2011/874302 - 32. El Naschie, M.S. (2016) The Emergence of Spacetime from the Quantum in Three Steps. Advances in Pure Mathematics, 6, 446-454.
http://dx.doi.org/10.4236/apm.2016.66032 - 33. Whiston, G.S. (1974) “Hyperspace” (The Cobordism Theory of Spacetime). International Journal of Theoretical Physics, 11, 285-288.
http://dx.doi.org/10.1007/BF01808083 - 34. Yodziz, P. (1973) Lorentz Cobordism. II. General Relativity and Gravitation, 4, 299-307.
http://dx.doi.org/10.1007/BF00759849 - 35. Atiyah, M.F. (1961) Bordism and Cobordism. Mathematical Proceedings of the Cambridge Philosophical Society, 57, 200-208.
http://dx.doi.org/10.1017/S0305004100035064 - 36. Milnor, J. (1962) A Survey of Cobordism Theory. L’Enseignement Mathematique Revue International. IIeSerie, 8, 16-23.
- 37. Pontryagin, L. (1959) Smooth Manifold and Their Application in Homotopy Theory. In: American Mathematical Society Translations, Series 2, Vol. II, American Mathematical Society, Providence, 1-114.
- 38. Thom, R. (1954) Quelques propriétés globales des variétés différentiables. Commentarii Mathematici Helvetici, 28, 17-86.
http://dx.doi.org/10.1007/BF02566923 - 39. Connes, A., Lichnerowicz, A. and Schützenberger, M.P. (2001) Triangle of Thought. American Mathematical Society, Providence, Rhode Island, USA.
- 40. Changeux, J.P. and Connes, A. (1995) Conversations on Mind, Matter and Mathematics. Princeton University Press, Princeton, New Jersey, USA.
- 41. Marcolli, M. (2010) Feynman Motives. World Scientific, Singapore.
- 42. Connes, A. and Marcolli, M. (2008) Noncommutative Geometry, Quantum Fields and Motives. American Mathematical Society, Rhode Island, USA.
- 43. Scheck, F., Upmeier, H. and Werner, W., Eds. (2002) Noncommutative Geometry and the Standard Model of Elementary Particle Physics. Springer, Berlin, Germany.
http://dx.doi.org/10.1007/3-540-46082-9 - 44. El Naschie, M.S. (1996) Kolmogorov Turbulence, Apollonian fractals and the Cantorian Model of Quantum Spacetime. Chaos, Solitons & Fractals, 7, 147-149.
http://dx.doi.org/10.1016/0960-0779(95)00123-9 - 45. Landi, G. (1997) An Introduction to Noncommutative Spaces and Their Geometrics. Springer, Berlin. (See in particular pp. 73-77)
- 46. El Naschie, M.S. (1998) Penrose Universe and Cantorian Spacetime as a Model for Noncommutative Quantum Geometry. Chaos, Solitons & Fractals, 9, 931-933.
http://dx.doi.org/10.1016/S0960-0779(98)00077-0 - 47. El Naschie, M.S. (1998) von Neumann Geometry and E-Infinity Quantum Spacetime. Chaos, Solitons & Fractals, 9, 2023-2030.
- 48. Goldfain, E. (2004) On a Possible Evidence for Cantorian Space-Time in Cosmic Ray Astrophysics. Chaos, Solitons & Fractals, 20, 427-435.
http://dx.doi.org/10.1016/j.chaos.2003.10.012 - 49. He, J.-H., Zhong, T., et al. (2011) The Important of the Empty Set and Noncommutative Geometry in Underpinning the Foundations of Quantum Physics. Nonlinear Science Letters B, 1, 14-23.
- 50. Marek-Crnjac, L. (2011) The Physics of Empty Sets and the Quantum. Nonlinear Science Letters B, 1, 8-9.
- 51. Mandelbrot, B. (1990) Negative Fractal Dimensions and Multifractals. Physica A: Statistical Mechanics and its Applications, 163, 306-315.
http://dx.doi.org/10.1016/0378-4371(90)90339-T - 52. El Naschie, M.S. (1996) On Numbers, Probability and Dimensions. Chaos, Solitons & Fractals, 7, 955-959.
http://dx.doi.org/10.1016/0960-0779(96)00036-7 - 53. El Naschie, M.S. (1994) On Certain “Empty” Cantor Sets and Their Dimensions. Chaos, Solitons & Fractals, 4, 293-296.
http://dx.doi.org/10.1016/0960-0779(94)90152-X - 54. El Naschie, M.S. (1993) Statistical Mechanics of Multi-Dimensional Cantor Sets, Gödel Theorem and Quantum Spacetime. Journal of Franklin Institute, 330, 199-211.
http://dx.doi.org/10.1016/0016-0032(93)90030-X - 55. El Naschie, M.S. (2006) New Hot Paper Comments. ESI Special Topics, Thomson Essential Science Indicators, September 2006.
- 56. El Naschie, M.S. (2004) A Review of E-Infinity Theory and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 57. El Naschie, M.S. (1998) On the Uncertainty of Cantorian Geometry and the Two-Slit Experiment. Chaos, Solitons & Fractals, 9, 517-529.
http://dx.doi.org/10.1016/S0960-0779(97)00150-1 - 58. El Naschie, M.S. (2005) On a Fuzzy Kähler-Like Mani-fold Which Is Consistent with the Two Slit Experiment. International Journal of Nonlinear Sciences and Numerical Simulation, 6, 95-98.
http://dx.doi.org/10.1515/ijnsns.2005.6.2.95 - 59. El Naschie, M.S. (2000) On the Unification of Heterotic Strings, M Theory and E(∞) Theory. Chaos, Solitons & Fractals, 11, 2397-2408.
http://dx.doi.org/10.1016/S0960-0779(00)00108-9 - 60. El Naschie, M.S. (2006) Elementary Prerequisites for E-Infinity (Recommended Background Readings in Nonlinear Dynamics, Geometry and Topology). Chaos, Solitons & Fractals, 30, 579-605.
http://dx.doi.org/10.1016/j.chaos.2006.03.030 - 61. El Naschie, M.S. (2004) The Concepts of E-Infinity: An Elementary Introduction to the Cantorian-Fractal Theory of Quantum Physics. Chaos, Solitons & Fractals, 22, 495-511.
http://dx.doi.org/10.1016/j.chaos.2004.02.028 - 62. El Naschie, M.S. (2009) Wild Topology, Hyperbolic Geometry and Fusion Algebra of High Energy Particle Physics. Chaos, Solitons & Fractals, 13, 1935-1945.
http://dx.doi.org/10.1016/S0960-0779(01)00242-9 - 63. El Naschie, M.S. (2004) Quantum Gravity from Descriptive Set Theory. Chaos, Solitons & Fractals, 19, 1339-1344.
http://dx.doi.org/10.1016/j.chaos.2003.08.009 - 64. El Naschie, M.S. (1995) A Note on Quantum Mechanics, Diffusional Interference and Information. Chaos, Solitons & Fractals, 5, 881-884.
http://dx.doi.org/10.1016/0960-0779(95)00040-B - 65. El Naschie, M.S. (1993) On Dimensions of Cantor Set Related Systems. Chaos, Solitons & Fractals, 3, 675-685.
http://dx.doi.org/10.1016/0960-0779(93)90053-4 - 66. El Naschie, M.S. (1997) Fractal Gravity and Symmetry Breaking in a Hierarchical Cantorian Space. Chaos, Solitons & Fractals, 8, 1865-1872.
http://dx.doi.org/10.1016/S0960-0779(97)00039-8 - 67. El Naschie, M.S. (1997) Remarks on Super Strings, Fractal Gravity, Nagasawa’s Diffusion and Cantorian Spacetime. Chaos, Solitons & Fractals, 8, 1873-1886.
http://dx.doi.org/10.1016/S0960-0779(97)00124-0 - 68. El Naschie, M.S. (2003) Modular Groups in Cantorian E(∞) High Energy Physics. Chaos, Solitons & Fractals, 16, 353-366.
http://dx.doi.org/10.1016/S0960-0779(02)00440-X - 69. El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508.
http://dx.doi.org/10.1016/0960-0779(95)00052-6 - 70. El Naschie, M.S. (2006) Hilbert Space, the Number of Higgs Particles and the Quantum Two-Slip Experiment. Chaos, Solitons & Fractals, 27, 9-13.
http://dx.doi.org/10.1016/j.chaos.2005.05.010 - 71. El Naschie, M.S. (2006) The Idealized Quantum Two-Slit Gedanken Experiment Revisited—Criticism and Reinterpretation. Chaos, Solitons & Fractals, 27, 843-849.
http://dx.doi.org/10.1016/j.chaos.2005.06.002 - 72. El Naschie, M.S. (2003) The VAK of Vacuum Fluctuation: Spontaneous Self-Organization and Complexity Theory Interpretation of High Energy Particle Physics and the Mass Spectrum. Chaos, Solitons & Fractals, 18, 401-420.
http://dx.doi.org/10.1016/S0960-0779(03)00098-5 - 73. El Naschie, M.S. (2005) Non-Euclidean Spacetime Structure and the Two-Slit Experiment. Chaos, Solitons & Fractals, 26, 1-6.
http://dx.doi.org/10.1016/j.chaos.2005.02.031 - 74. El Naschie, M.S. (2006) Hilbert, Fock and Cantorian Spaces in the Quantum Two-Slit Gedanken Experiment. Chaos, Solitons & Fractals, 27, 39-42.
http://dx.doi.org/10.1016/j.chaos.2005.04.094 - 75. El Naschie, M.S. (2006) On an Eleven Dimensional E-Infinity Fractal Spacetime Theory. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 407-409.
- 76. El Naschie, M.S. (2006) Fuzzy Dodecahedron Topology and E-Infinity Spacetime as a Model for Quantum Physics. Chaos, Solitons & Fractals, 30, 1025-1033.
http://dx.doi.org/10.1016/j.chaos.2006.05.088 - 77. El Naschie, M.S. (2006) On Two New Fuzzy Kähler Manifolds, Klein Modular Space and ’t Hooft Holographic Principles. Chaos, Solitons & Fractals, 29, 876-881.
http://dx.doi.org/10.1016/j.chaos.2005.12.027 - 78. El Naschie, M.S. (2003) Complex Vacuum Fluctuation as a Chaotic “Limit” Set of Any Kleinian Group Transformation and the Mass Spectrum of High Energy Particle Physics via Spontaneous Self Organization. Chaos, Solitons & Fractals, 17, 631-638.
http://dx.doi.org/10.1016/S0960-0779(02)00630-6 - 79. El Naschie, M.S. (2006) Superstrings, Entropy and the Elementary Particles Content of the Standard Model. Chaos, Solitons & Fractals, 29, 48-54.
http://dx.doi.org/10.1016/j.chaos.2005.11.032 - 80. El Naschie, M.S. (1999) Nuclear Spacetime Theories, Super-strings, Monster Group and Applications. Chaos, Solitons & Fractals, 10, 567-580.
http://dx.doi.org/10.1016/S0960-0779(98)00313-0 - 81. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
http://dx.doi.org/10.4236/jqis.2011.12007 - 82. El Naschie, M.S. (2004) The Symplictic Vacuum, Exotic Quasi Particles and Gravitational Instanton. Chaos, Solitons & Fractals, 22, 1-11.
http://dx.doi.org/10.1016/j.chaos.2004.01.015 - 83. El Naschie, M.S. (1998) COBE Satellite Measurement, Hyper Spheres, Superstrings and the Dimension of Spacetime. Chaos, Solitons & Fractals, 9, 1445-1471.
http://dx.doi.org/10.1016/S0960-0779(98)00120-9 - 84. El Naschie, M.S. (2006) Advanced Prerequisites for E-Infinity Theory. Chaos, Solitons & Fractals, 30, 636-641.
http://dx.doi.org/10.1016/j.chaos.2006.04.044 - 85. Birrell, N. and Davies, P. (1984) Quantum Fields in Curved Space. Cambridge University Press, Cambridge, UK. (See in particular pages 20 and 34)
- 86. Johnson, C.V. (2003) D-Branes. Cambridge University Press, Cambridge, UK. (See in particular pages 85-87 for conformal ghosts and page 43 for negative norm states)
- 87. He, J.-H., et al. (2005) Transfinite Physics: A Collection of Publications on E-Infinity Cantorian Spacetime Theory. China Science & Culture Publishing.
- 88. Kaku, M. (1993) Quantum Field Theory. Oxford University Press, Oxford.
- 89. Polchinski, J. (1999) String Theory. Vol. I. Cambridge University Press, Cambridge.
- 90. Das, A. (2008) Lectures on Quantum Field Theory. World Scientific, Singapore (See in particular pages 522-550 where one finds excellent information about ghost action, ghost fields, ghost number, ghost scaling and the connected symmetry)
- 91. ‘t Hoof, G. (1994) Under the Spell of the Gauge Principle. World Scientific, Singapore.
- 92. Weinberg, S. (1995) The Quantum Theory of Fields: Vol. I. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139644167 - 93. Weinberg, S. (1996) The Quantum Theory of Fields: Vol. II. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139644174 - 94. Weinberg, S. (2000) The Quantum Theory of Fields: Vol. III. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139644198 - 95. Penrose, R. (2004) The Road to Reality. J. Cape, London, UK.
- 96. Susskind, L. and Lindesay, J. (2005) The Holographic Universe. World Scientific, Singapore.
- 97. El Naschie, M.S. (1993) Gödel, Cantor and Modern Nonlinear Dynamics. In: Wolkowski, Z.W., Ed., 1st International Symposium on Gödel’s Theorems, World Scientific, Singapore, 95-106.
- 98. ‘t Hoof, G. (2005) 50 Years of Yang-Mills Theory. World Scientific, Singapore.
- 99. Wittgenstein, L. (1961) Tractatus Logico-Philosphicus. Routledge and Kegan Paul, London.



