Received 28 May 2016; accepted 27 June 2016; published 30 June 2016

ABSTRACT

In this paper, we are concerned with a class of second-order nonlinear differential equations with damping term. By using the generalized Riccati technique and the integral averaging technique of Philos-type, two new oscillation criteria are obtained for every solution of the equations to be oscillatory, which extend and improve some known results in the literature recently.

Keywords:

Oscillation Criterion, Differential Equations with Damping, Integral Averaging Method

1. Introduction

Zhang and Yan discussed respectively the solutions’ oscillation of the second order nonlinear differential equation with damping in [1] - [3]

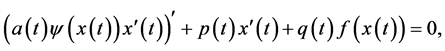(1)

and obtained some useful results. On this basis, the paper continues this discussion of Equation (1). For Equation (1), assume that

(A₁) 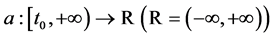is continuously differentiable;

(A₂) are continuous functions, and for arbitrarily large t, , 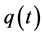can change sign;

(A₃) 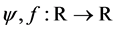is continuously differentiable and when, , ,.

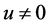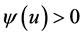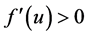In this paper, we assume that each solution 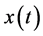of Equation (1) can be extended to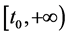. A solution is said to be regular if there exists t on arbitrary interval, such that. A regular solution is said to be oscillatory, if it has arbitrarily large zeros; otherwise it is said to be nonoscillatory. Equation (1) is called oscillatory if all its regular solutions are oscillatory.

Many exceptions of Equation (1) have emerged in the literature, for example, the paper [4] discussed the oscillation of the second order linear differential equation with damping

(2)

and the associated equations have been studied by many authors with a number of important results of oscillation. We recommend References [5] - [7] and their introductions. The purpose of this paper is to establish the Philos-type oscillation criteria of Equation (1) in general conditions. By using the generalized Riccati transformation and integral averaging technique of Philos-type [8] , we obtain three new oscillatory criteria for Equation (1). Our results generalize, improve and unify the above results in above references and the method of proof is also relatively simpler than their’s. The functions inequalities in this article are established for all sufficiently large t if there is no particular explanation.

2. Main Results

Using Philos-type integral average conditions, the new oscillatory results of Equation (1) is given as below. Function classes P is introduced, we define that

(3)

is called function belong to the class P, if there is satisfying

1);;

2) H exists non-positive and continuously partial derivatives for the second variable in, and satisfies the equation

(4)

Theorem 1. Assume that (A₁) - (A₃) hold, and,. The function belongs to the class of functions P and (4) holds. If there is an continuously differentiable function

making

(5)

then Equation (1) is oscillatory.

Proof. Suppose that is a nonoscillatory solution of Equation (1). We may assume without loss of gene- rality that with. we consider the function

(6)

From Equation (1), we get

So when we have

(7)

By the division integral formula and applying Equation (4), we have

(8)

So when, it follows

(9)

By (9), when, we get

(10)

The two sides of (10) are divided by, and we calculate the limit of the two sides of (10) when. So we have a contradiction to the condition (5). This completes the proof.

Corollary 1. In Theorem 1, if the condition (5) is replaced by the following conditions:

1)

2)

(11)

then Equation (1) is oscillatory.

Remark 1. In Theorem 1, if we select different functions and the different oscillation criteria

of Equation (1) can be obtained. For example, you can select or.

If the condition (5) is not satisfied, we can apply the following guidelines for determining oscillation of Equation (1).

Theorem 2. Assume that (A₁) - (A₃) hold, and. belongs to the class of functions P and (4) holds. Besides,

(12)

If there is a continuously differentiable function to make

(13)

and continuously function to make

(14)

hold when. Besides,

(15)

where. Then Equation (1) is oscillatory.

Proof. Suppose that is a nonoscillatory solutions of (1). And when, Define

(16)

We can get (10) as the proof of Theorem 1, i.e.

(17)

The two sides of the above result are divided by, then we calculate the limit of the two sides when. By (14), we get So

(18)

Define

(19)

By (9), we have

(20)

and by (14), we get

(21)

and

(22)

By (13) and (22) there is a sequence

(23)

such that

(24)

When we calculate the supper limit of (20) and apply (21), it follows

(25)

So for sufficiently large n, there is

(26)

Because

(27)

is increasing, we get Where or is a positive constant. Assume that, then

and by (26), we have

(28)

From (26) and (28), where is a constant.That is for sufficiently large

(29)

On the other hand, by the Schwarz inequality, we get

(30)

So

(31)

From (24), we have

(32)

There is an contradiction with (28) and (29). If with (18) we get

(33)

we obtain a contradiction to (15). This completes the proof. □

Remark 2. The theorems of this paper improve or extend the results in [1] - [12] . For Equation (1), Theorem 1 and 2 are new.

Finally, we give two examples.

Example 1. Consider the second-order differential equation with damping

(34)

where.

Now let, , , It is easy to verify that Equation (34) satisfies all the conditions of Theorem 1, so by Theorem 1, Equation (34) is oscillatory.

Example 2. Consider the second-order differential equation with damping

(35)

Here.

Now let, , , , so all the conditions of Theorem 2 are satis-

fied. By Theorem 2, Equation (35) is oscillatory on. But the other known results cannot be applied in Equation (35).

3. Conclusions and Outlook

In this paper, the two well-known results of Philos on the second order linear differential equation are extended to the second order nonlinear differential equations with damping term. As we all know, the motions under ideal conditions and vacuum are rare, but the motions with damping and disturbances are widespread. The discussion on the oscillation of the differential equation with damping term in our paper is of more practical significance. Moreover, the previous study on oscillation of the equation always assumed that, but the sign of and in our paper may change. Therefore, in this paper we extend and improve some of the results that are known in the previous study.

It is a deficiency of this paper that there is no discussion on delay. So in the follow-up study we will discuss the oscillation of the second order delay differential equations with damping, second order neutral delay differential equations and higher order delay differential equations with damping.

Acknowledgements

We thank the Editor and the referee for their comments. Research of Q. Zhang is funded by the Natural Science Foundation of Shandong Province of China grant ZR2013AM003. This support is greatly appreciated.

Cite this paper

Quanxin Zhang,Xia Song,Shouhua Liu, (2016) New Oscillation Criteria for the Second Order Nonlinear Differential Equations with Damping. Journal of Applied Mathematics and Physics,04,1179-1185. doi: 10.4236/jamp.2016.47122

References