Journal of Applied Mathematics and Physics
Vol.04 No.10(2016), Article ID:71195,10 pages
10.4236/jamp.2016.410187
Chaos in Time Series of Sakarya River Daily Flow Rate
Haci Ahmet Yildirim1, Avadis Simon Hacinliyan2,3, Ergun Eray Akkaya2*, Cercis Ikiel4
1Department of Physics, Sakarya University, Adapazari, Turkey
2Department of Physics, Yeditepe University, Istanbul, Turkey
3Department of Information Systems and Technologies, Yeditepe University, Istanbul, Turkey
4Department of Geography, Sakarya University, Adapazari, Turkey

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 9, 2016; Accepted: October 10, 2016; Published: October 13, 2016
ABSTRACT
In this study, possible low dimensional chaotic behavior of Sakarya river flow rates is investigated via nonlinear time series techniques. To reveal the chaotic dynamics, the maximal positive Lyapunov exponent is calculated from the reconstructed phase space, which is obtained using the phase space reconstruction method. The method reconstructs a phase space from the scalar time series, which depicts the real system’s invariants Positive values, because the Lyapunov exponent values calculated using the appropriate software program indicate possibility of chaotic behavior. Analyzed data involve the monthly average flow rates of eleven main branches of Sakarya River through the years 1960-2000.
Keywords:
Chaos Theory, Time Series Analysis, Lyapunov Exponent, Mutual Information, False Nearest Neighbors

1. Introduction: Sakarya River Flow Using Low Dimensional Deterministic Techniques
Sakarya River is one of the longest rivers in western region of Turkey. It originates in the western part of Central Anatolia, but predominantly traverses the Marmara region and flows to the Black Sea. Its basin is 58,160 km2; its length is approximately 810 km and width is about 60 - 150 m [1] . Figure 1 shows its flow map. It has lots of tributaries, for example, Porsuk, Ankara, Goynuk and Kirmir rivulets.
A natural phenomenon like river flow is a highly complicated one and usually treated as nondeterministic. Understanding the behavior of its underlying dynamics will lead to a more reliable base for choosing an appropriate modeling and prediction method.
Figure 1. Location map of Sakarya River.
Some recent studies [2] have shown that low-dimensional deterministic techniques can be applied as an alternative method for modeling and the results are encouraging. A complicated behavior in nature can be identified as deterministic and chaotic or nondeterministic and random, subject to its underlying dynamics. The use of low dimensional deterministic and chaotic time series techniques in studying, modeling and possibly predicting river flow dynamics is increasing; encouraging results are being obtained. As long as a sufficient amount of care is exercised in applying low-dimensional deterministic techniques and in interpreting the findings, such techniques can be useful in studying dynamics of river flow [2] . In addition, recent articles [3] [4] on flow prediction using chaos theory can reveal the number of variables that influence the river flow dynamics. This shows nonlinear analysis is gaining importance and usefulness for river flow analysis.
Observational data obtained from the natural phenomena add another complication by way of measurement errors and scalar values which purely represent the underlying dynamical system. A well-known and widely used approach to overcome these difficulties is the phase space reconstruction method. Based on the theorem of Takens, one can construct a phase space which successively resembles the global behavior of the original dynamical system from scalar measurements. A brief outline of the technique is given in Figure 2. When one observes complicated behavior in nature, one seeks a simple underlying cause. If we have only experimental or observational data at our disposal and in most cases, the data are one dimensional, involving a single sequence of measurements at equal time intervals (a time series), and one would try to extract information from it to ascertain whether the dynamics is deterministic and chaotic or nondeterministic and random. In this study, the flow discharge data obtained from monthly averages of Sakarya River and its eleven tributaries are analyzed to reveal the characteristics of its flow dynamics which will be a guideline for modeling the flow discharge. The experimental data involve the average monthly discharge rate of Sakarya River. The data have only scalar values and are taken from the [5] EIE (General Directorate of Electrical Power Resources Survey and Development Administration). Fifty-four stream flow observation stations have been set on the Sakarya River by the EIE and the observation period spans the period 1960 to 2000.
In Figure 2, from 1960 to 2000 every months’ average flow rate in m3/s unit are collected from EIE. The flow rates for each tributary show similar patterns in spite of the fact that Sakarya River covers a relatively large and varied region involving two different climatic regions. Hence, the Dogancay tributary has characteristics similar to the Sakarya River. In Figure 3, similar data for the Aktas River which is another tributary of Sakarya River are shown. The similarity is apparent.
The time series analysis method applied in this work can be divided into the following steps; observing a one dimensional signal in uniform time interval x(0), x(T), …, x(n, T), phase space reconstruction, and calculation of invariants of the reconstructed dynamics.
Figure 2. Flow rate data on given months of Dogancay tributary.
Figure 3. Flow rate data on given months of Aktas tributary.
2. Phase Space Reconstruction
As the scalar measurements are taken at arbitrary time intervals, a suitable delay time is the key point to preserve the global behavior of the dynamics.
In order to start the phase space reconstruction from the scalar flow rate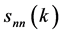 , where k is the time step, we need to construct the delay vector
, where k is the time step, we need to construct the delay vector 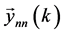 given by;
given by;
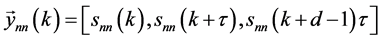 (1)
(1)
τ is the delay time and d means the embedding dimension. The time delay can be found from the first zero of the correlation function (linear criterion) or first minimum of the average mutual information [6] .
A small delay time can lead to a strongly correlated phase space vectors; on the other hand, information loss is inevitable if a large delay time value; the delay time can be estimated from either the mutual information or the autocorrelation.
One can see both periodic and irregular behavior in Figure 4. A study of the correlation function confirms this conjecture. For example, the correlation function for the Aktas tributary, shows a decrease up to about 7 - 8 months. But the correlation function never reaches zero. It then reveals a periodic behavior involving approximately 40 months. If multiple time scales are involved, a choice must be made between the zero of the correlation function and the first minimum of the mutual information. Although there is no clear indication of consistent success, the latter is usually preferred.
2.1. Mutual Information Is Basically the Information Carried from One Random Variable to Another One
Mutual information is information between two random variables. We can only see the information sent to a given channel by receiving the corresponding information from the same channel.
In Figure 5 a brief outline of the technique is given. One can see demonstrating steps
Figure 4. Correlation for the Aktas subriver.
Figure 5. Figure demonstrating steps of data analysis in time series.
of data analysis in time series.
Let X and Y be a random variables having a joint probability distribution given by p(X, Y). If X and Y, have individual probability distributions given by p(X) and p(Y) respectively, the entropy is calculated as the distance between the mutual information assuming equal distribution and the actual multiple distributions, given by the equations below:
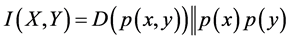 (2)
(2)
Mutual information is usually calculated using time delayed vectors reconstructed from the scalar time series as suggested by Fraser and Swinney [6] as a tool to determine a conceivable delay. Besides, the mutual information considers nonlinear correlations. For doing this one has to compute;
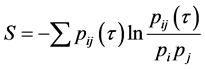 (3)
(3)
Here, 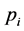 and
and 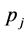 are the probabilities to find a given value in the i-th and j-th intervals of the time series and
are the probabilities to find a given value in the i-th and j-th intervals of the time series and  is joint probability that a given observation falls into the i-th interval at a given time and in the j-th one after a delay time τ. Theoretically there should be no relevance on the amount of separation if there is no correlation. This value can easily be calculated. There are acceptable arguments that a marked minimum at a certain value of j, in the time delayed mutual information gives a good estimate for a reasonable time delay. However, if we use a too long time delay, the correlations between the components of reconstructed vectors will be lost and signals will be mistakenly recognized as if it were a random signal, rather than coming from a possibly finite prediction horizon related to the maximal Lyapunov exponent. Mutual information is important for our determining maximal Lyapunov exponent as mentioned in [7] .
is joint probability that a given observation falls into the i-th interval at a given time and in the j-th one after a delay time τ. Theoretically there should be no relevance on the amount of separation if there is no correlation. This value can easily be calculated. There are acceptable arguments that a marked minimum at a certain value of j, in the time delayed mutual information gives a good estimate for a reasonable time delay. However, if we use a too long time delay, the correlations between the components of reconstructed vectors will be lost and signals will be mistakenly recognized as if it were a random signal, rather than coming from a possibly finite prediction horizon related to the maximal Lyapunov exponent. Mutual information is important for our determining maximal Lyapunov exponent as mentioned in [7] .
2.2. False Nearest Neighbors
One of the main problems of reconstructing a phase space from a scalar time series is choosing a suitable embedding dimension, which will at least topologically preserve the global properties of the dynamical system. Embedding dimension directly affects the attractor trajectory in the phase space, which alters the neighborhood of the points. If the embedding dimension is chosen to be smaller than the actual attractor dimension, projection of the trajectory will map false values into other neighborhoods of values; these are called the false neighbors. The calculation goes as follows: Choose a vector  constructed using the delay time suggested by mutual information and calculate the distance between its nearest neighbors
constructed using the delay time suggested by mutual information and calculate the distance between its nearest neighbors 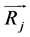 in an arbitrary dimension. Iterate this procedure for all the successive vectors and calculate Ri using the following equation.
in an arbitrary dimension. Iterate this procedure for all the successive vectors and calculate Ri using the following equation.
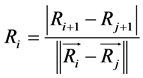 (4)
(4)
A point of data is selected as a false neighbor if the distance, Ri exceeds a given threshold. A typical false neighbor’s calculation is shown in Figure 6.
3. Calculation of the Maximal Lyapunov Exponent
Lyapunov exponent is a measure of divergence or convergence of orbits in a phase space, which can also be calculated for a time series. As the reconstructed phase space preserves the topology of the underlying dynamics, Lyapunov exponents calculated for the embedded phase space will show chaotic nature of the original attractor. The rate of exponential growth between the nearby trajectories is called as the maximal Lyapunov exponent and a positive rate indicates chaotic behavior. The following equation is used to calculate the stretching of the trajectories;
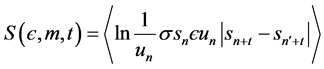 (5)
(5)
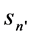 is a neighboring point to sn in the phase space in the course of the attractor; є is the box size. At a future time t the distance between these points will be
is a neighboring point to sn in the phase space in the course of the attractor; є is the box size. At a future time t the distance between these points will be

4. Results
Table 1 shows us mutual information values, embedding dimension values and Lyapr values which are the largest Lyapunov exponent of a given scalar data set using the
Figure 6. Graph of False-Nearest neighbors for botbasi tributary of Sakarya river.
Table 1. Nonlinear time series analysis results of Sakarya river’s tributaries.
algorithm of Rosenstein et al. [8] (this is claimed to be a better estimate for smaller data sets as explained below). Lyapk values are largest Lyapunov exponent of a given scalar data set using the algorithm of Kantz [9] , with further explanation in [9] . In order to find Lyapunov exponent, we use the mutual information values calculated by the mutual package in TISEAN by observing its first minimum. We get the embedding dimension by the false-nearest technique. In order to calculate the Lyapunov exponent, we calculate the distance between two neighboring points as a function of the separation t on a semilogarithmic plot is used. The Lyapunov exponent is estimated from the slope and their values have a standard deviation of ±0.01.
The algorithm proposed by Kantz establishes that the rate of divergence of nearby trajectories can fluctuate along the trajectory and the amount of fluctuation depends on the stretching and folding of the phase space as given by the spectrum of effective Lyapunov exponents. Rosenstein et al. [8] proposed a systematic algorithm where the distance between the trajectories is calculated by the Euclidian norm in the reconstructed phase space. They use only one neighbor trajectory which makes the method more suitable for shorter time series. Thus, the algorithm suggested by Rosenstein is more effective when the number of data is relatively small. In our study, the results obtained from each algorithm are in parallel with each other. A typical Lyapunov Exponent by stretching exponent calculation using the Rosenstein approach is illustrated in Figure 7, while the calculation using the standard Kantz approach is illustrated in Figure 8. The Kanz algorithm [9] makes use of the statistical properties of the local divergence rates of nearby trajectories. It does not need correct embedding dimension. These figures demonstrate a positive slope and as mentioned above, show positive maximal Lyapunov exponents which in turn indicates chaotic behavior. We also use Kanz algorithm to ensure positive maximal Lyapunov exponent. The statistical issues involved in the selection of the approach are discussed extensively in [10] and [11] .
Figure 7. Stretching factor vs. iteration graph using the Rosenstein algorithm.
Figure 8. Stretching factor vs. iteration graph using the Kantz algorithm.
Table 1 shows mutual information, embedding dimension value and Lyapr value (the largest Lyapunov exponent of a given scalar data set using the algorithm of Rosenstein et al. [8] ); for each tributary of Sakarya river (this is claimed to be a better estimate for smaller data sets as explained below). Lyapk values are largest Lyapunov exponent of a given scalar data set using the algorithm of Kantz [9] .
5. Conclusions
Understanding the dynamics of river flow is crucial to select a feasible modeling method to forecast river discharge. In this study, phase space reconstruction method is used to obtain a depiction of the underlying dynamics, which will preserve the global invariants of the system. Maximal Lyapunov exponents which constitute a very strong evidence for chaotic behavior for eleven tributaries of the Sakarya River have been calculated. These results are encouraging for applying chaotic modeling routines instead of probabilistic methods.
As a result, monthly mean flow values of Sakarya River show chaotic behavior as quantified by the maximal Lyapunov Exponent. That may imply that the river has no long time trend, which is observed by [1] . One can say climate changes and huge amount of usage of the river’s water and dam constructions may cause to decrease trend. According to article [12] , Benue River in Nigeria has a comparable trend but no low dimensional phase space chaotic dynamics has been observed there. Therefore, we can say Sakarya River has limited future for electricity from dams and other human exploitation because of its chaotic dynamics. We have studied the article by S. Isik et al. [13] that reaches the same conclusions using quasi-linear time series analysis methods from regular statistical analysis. This work corroborates the findings and finally demonstrates that the phenomenon may be better understood by nonlinear time series analysis than stochastic techniques. This work is also relevant for identifying the river’s complex behavior since it tries to use nonlinear techniques in river systems which come from the theory of complex systems [14] .
Cite this paper
Yildirim, H.A., Hacinliyan, A.S., Akkaya, E.E. and Ikiel, C. (2016) Chaos in Time Series of Sakarya River Daily Flow Rate. Journal of Applied Mathematics and Physics, 4, 1849-1858. http://dx.doi.org/10.4236/jamp.2016.410187
References
- 1. Atalay, A. and Ikiel, C. (2007) Trend Analysis of Monthly and Annual Flow Values of Sakarya River. GEOMED 2007 International Symposium, Turkey, 5-8 June 2007.
- 2. Sivakumar, B. (2003) Evidence of Low-Dimensional Determinism in River Flow Dynamics: Examples from Predictions.
- 3. Adenan, N.H. and Noorani, M.S. (2014) Nonlinear Prediction of River Flow in Different Watershed Acreage. Journal of Korean Society of Civil Engineering, 18, 2268-2274.
http://dx.doi.org/10.1007/s12205-014-0646-4 - 4. Khatibi, R., Sivakumar, B., Ghorbari, M.A., Kisi, O., Kocak, K. and Zadeh, D.F. (2012) Investigating Chaos in River Stage and Discharge Time Series. Journal of Hydrology, 414-415, 108-117.
http://dx.doi.org/10.1016/j.jhydrol.2011.10.026 - 5. EIE (2003) Monthly Mean Flows of Turkey Rivers (1935-2000).
- 6. Fraser, A.M. and Swinney, H.L. (1986) Independent Coordinates for Strange Attractors from Mutual Information. Physical Review A, 33, 1134.
http://dx.doi.org/10.1103/PhysRevA.33.1134 - 7. Hegger, R., Kantz, H. and Schreiber, T. (1999) Practical Implementation of Nonlinear Time Series Methods: The TISEAN Package. Chaos, 9, 413.
http://dx.doi.org/10.1063/1.166424 - 8. Rosenstein, M.T., Collins, J.J. and De Luca, C.J. (1993) A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets. Physics D, 65, 117.
- 9. Kantz, H. (1994) A Robust Method to Estimate the Maximal Lyapunov Exponent of a Time Series. Physics Letters A, 185, 77.
http://dx.doi.org/10.1016/0375-9601(94)90991-1 - 10. Pompe, B. (1993) Measuring Statistical Dependences in a Time Series. Journal of Statistical Physics, 73, 587.
http://dx.doi.org/10.1007/BF01054341 - 11. Palus, M. (1995) Testing for Nonlinearity Using Redundancies: Quantitative and Qualitative Aspects. Physica D, 80, 186.
http://dx.doi.org/10.1016/0167-2789(95)90079-9 - 12. Martins, O., Sadeeq, M.A. and Ahaneku, I.E. (2011) Nonlinear Deterministic Chaos in Benue River Flow Daily Time Sequence. Journal of Water Resource and Protection, 3, 747-757.
- 13. Isik, S., Dogan, E., Kalin, L., Sasal, M. and Agiralioglu, N. (2008) Effects of Anthropogenic Activities on the Lower Sakarya River. Elsevier Catena, 75, 172-181.
- 14. Schleiss, A.J., de Cesare, G., Franca, M.J. and Pfister, M. (2014) River Flow 2014. CRC Press, Abington, 424 p.










