Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:65855,9 pages
10.4236/jamp.2016.44078
Measuring the Evolution and Influence in Society’s Information Networks
Xiaocun Mao, Tingting Dong, Meng Li, Zhenping Li
School of Information, Beijing Wuzi University, Beijing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 March 2016; accepted 23 April 2016; published 26 April 2016
ABSTRACT
We develop a series of mathematical models to describe flow of information in different periods of time and the relationship between flow of information and inherent value. We optimize the diffusion mechanism of information based on model SEIR and improve the diffusion mechanism. In order to explore how inherent value of the information affects the flow of information, we simulate the model by using Matalab. We also use the data that the number of people is connected to Internet in Canada from the year 2009 to 2014 to analysis the model’s reliability. Then we use the model to predict the communication networks’ relationships and capacities around the year 2050. Last we do sensitivity analysis by making small changes in parameters of simulation experiment. The result of the experiment is helpful to model how public interest and opinion can be changed in complex network.
Keywords:
Flow of Information, SEIR Model, Dynamic Equations, Complex Network

1. Introduction
Information sharing is the basis of human society. A history of communications advances a new theory of media that explains the origins and impact of different forms of communication on human history [1] . A disease transmission model of SEIRS type with distributed delays in latent and temporary immune periods is discussed. F. Capone (2014) studied a reaction-diffusion system in SEIR model for infections under homogeneous Neumann boundary conditions [2] . Zhang Wei (2014) used SEIR model to explore the mode of message spreading throughout the micro-blog network [3] . Xia Lingling (2015) proposed a modified SEIR model with hesitating mechanism to investigate the spreading threshold and the final rumor size [4] . Therefore, the flow of information spreading issues based on the complex social networks can be looked as a disease transmission model of SEIR. The basic form of information diffusion is in accord with that of epidemic spreading. In this paper, we assume that the basic form of information diffusion conforms to SEIR model. Thus the study of the problem of information spreading on the complex social networks has an important scientific significance for the authoritative organizations to make effective control strategies in case of emergency. Generally, physicists have divided the real world network into four categories: biological networks, network technology, information network, social network. In fact, information network and social network have been merged together. On the basis of assuming that the basic form of information diffusion conforms to SEIR model, studying the problem of information spreading on the complex social networks has an important scientific significance for the authoritative organizations to make effective control strategies in case of emergency.
With the development of human society, information transmitting media is evolved continually. Meanwhile, morphology, structure and characteristics of the human society network are also in constant change. The flow of information is influenced by many factors such as inherent value of information, degree distribution of nodes and so on. So we are required to explore the evolution of the methodology, purpose, and functionality of society’s networks by analyzing the relationship between flow of information and inherent value of information and analyzing how public interest and opinion can be changed through information networks.
2. Mathematical Model-Information Diffusion Model Based on Inherent Value of Information and Degree of Nodes
2.1. Assumptions
1) Given the complexity of calculation, we assume that information spreads on the small-world network. The small world network model is an actual complex network model which is located between the rules and random. Interpersonal relationship network as an example, most relationships may “short-range”, similar to the adjacent edges of the rules of the network model; many also have the distance relationships, similar to the remote jump edge [5] .
2) The basic form of information diffusion is in accord with that of epidemic spreading. In this paper, we assume that the basic form of information diffusion conforms to SEIR model.
2.2. Introduction of the Model
In SEIR model, people are divided into four classes [6] [7] :
・ The susceptible (S), who are susceptible to infection;
・ The exposed (E), who are affected but in the incubation;
・ The infectious (I), who are infected and have the symptom;
・ The recovered (R), who recover or survive.
The total population of the area is N, and
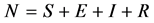 (1)
(1)
In this paper, first we optimize the diffusion mechanism of information based on model SEIR. We think that the exposed can be changed to the recovered with a probability. Second, another two factors are involved in our model: the effect of information value and the degree of nodes. We think information value has influence on the exposed and the degree of nodes has influence on information diffusion. So the effect of information value represents the probability with which the susceptible could be changed to the exposed. In the other hand, the degree distribution of nodes can be added to dynamic equations of information diffusion. Meanwhile, the degree distribution of nodes can reflect how network changes over time.
2.3. Model Construction
2.3.1. Step 1: The Diffusion Mechanism of the Improved SEIR Model
We optimize the diffusion mechanism of information based on SEIR model and the improved diffusion mechanism is shown as follows:
・ After the initial node releases the information, the susceptible has three transition states. First the susceptible could be changed to the exposed with the possibility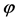 . Second, the susceptible could be changed to the recovered with the possibility
. Second, the susceptible could be changed to the recovered with the possibility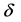 . Third, the susceptible could be changed to the infectious with the possibility
. Third, the susceptible could be changed to the infectious with the possibility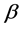 ;
;
・ The exposed could be changed to the infectious with the possibility 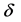 and it could also be changed to the recovered with the possibility
and it could also be changed to the recovered with the possibility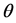 , and
, and
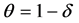 (2)
(2)
・ The infectious can be changed to the recovered with the probability of recovery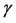 ;
;
・ The recovered can be changed to the infectious with the probability of recovery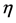 .
.
The flow chart of information diffusion is shown as follows (Figure 1):
2.3.2. Step 2: Quantification for the Effect of Information Value [8]
The effect of information value reflects in two aspects: the importance of the information for people and time effect of information. The effect of information value can represents the probability with which the susceptible could be changed to the exposed:
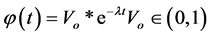 (3)
(3)
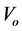 is the importance of the information for people and the value of
is the importance of the information for people and the value of 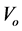 ranges from 0 to 1. 0 means information is not important for someone at all while 1 means information is the most important for someone;
ranges from 0 to 1. 0 means information is not important for someone at all while 1 means information is the most important for someone; 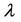 is the time effect of information. In other words, because there are a large quantity of information, people’s attention to information has time-effect and information value is inversely proportional to time.
is the time effect of information. In other words, because there are a large quantity of information, people’s attention to information has time-effect and information value is inversely proportional to time.
2.3.3. Step 3: The Establishment of Dynamic Equations
When we do not take the degree distribution of nodes into account,the dynamic equations of the improved SEIR model are displayed below:
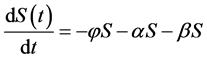
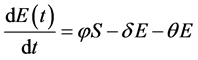 (4)
(4)
where 



However, in fact information spreads on the complex network. According to assumptions, we regard the complex network as a homogeneous network. In addition, the degree distribution of the homogeneous complex network and mean-field theory is [9] :

where 


Figure 1. Structure of SEIR information spreading process.
As a result, we establish final dynamic equations about density fluctuation based on Equations (4) and (5):

constraint condition:

where 




3. Analysis for What Qualifies as News
In order to explore how inherent value of the information affects flow of information, we simulate the model by using Matalab. The values of parameters are as follows:
By changing the value of
From the results, we can get some conclusions:
・ With the increase of
・ With the increase of
Figure 2.
Figure 3.
Figure 4.
Figure 5.
4. Model’s Reliability Analysis
In this paper, we define that the value added of people connected to Internet is the same as peak value of E. Because according to the two conclusions above, peak value of E means the number of people who are willing to connect to Internet to obtain the information whose 
The data is about the number of people connected to Internet in Canada from the year 2009 to 2014 [10] - [12] . The results are shown in Table 1 as follows:
According to the results, the value of 
5. Model’s Prediction Capacity
According to model’s reliability analysis, in order to predict the communication networks’ relationships and capacities around the year 2050, we have to predict every year from 2014. The results are shown in Table 2 as follows.
Table 1. Prediction results for today’s network.
Table 2. Prediction results for future.
Figure 6.
Figure 7.
Figure 8.
So we can know the number of nodes will reach 62,905,700 and the capacity of flow of information is doubled.
6. The Sensitivity Analysis
We make small changes in parameters by simulation experiment and find that 
・ We can learn that when 






7. Conclusions
In this paper, we propose a novel approach to organic SEIR model based on complex network topologies. By analyzing and simulating the different factors that affect the flow of information spread, we can get the relationship between flow of information and inherent value of the information.
1) Based on the experiments, the dynamic evolution of density fluctuation is simulated. The four dynamic equations reflect how the density of nodes in four different states varies over time. In the spread process, we conclude the main parameters by simulation experiment and find that 
2) Furthermore, we need to determine how information value, people’s initial opinion and bias, form of the message or its source, and the topology or strength of the information network in a region, country, or worldwide could be used to spread information and influence public opinion.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (71540028, F012408), and Major Research Project of Beijing Wuzi University. Funding Project for Technology Key Project of Municipal Education Commission of Beijing (ID: TSJHG201310037036); Funding Project for Beijing key laboratory of intelligent logistics system (No: BZ0211); Funding Project of Construction of Innovative Teams and Teacher Career Development for Universities and Colleges Under Beijing Municipality (ID: IDHT20130517); Funding Project for Beijing philosophy and social science research base specially commissioned project planning (ID: 13JDJGD013); Beijing Intelligent Logistics System Collaborative Innovation Center.
Cite this paper
Xiaocun Mao,Tingting Dong,Meng Li,Zhenping Li, (2016) Measuring the Evolution and Influence in Society’s Information Networks. Journal of Applied Mathematics and Physics,04,677-685. doi: 10.4236/jamp.2016.44078
References
- 1. Marshall, T.P. (2011) A History of Communications: Media and Society from the Evolution of Speech to the Internet (New York: Cam-bridge).
http://longfiles.com/3gaf63075hya/A_History_of_Communications_Media_and_Society_from_the_Evolution_of_Speech_to_the_Internet.pdf.html - 2. Capone, F., De Cataldis, V. and De Luca, R. (2014) On the Stability of a SEIR Reaction Diffusion Model for Infections under Neumann Boundary Conditions. Acta Applicandae Mathematicae, 132, 165-176.
http://dx.doi.org/10.1007/s10440-014-9899-7
http://www.medsci.cn/sci/show_paper.asp?id=7c9b9669200 - 3. Zhang, W., Bai, S. and Jin, R. (2014) The Model of Microblog Message Diffusion Based on Complex Social Network. International Journal of Modern Physics B, 28, Article ID: 1450136.
http://dx.doi.org/10.1142/s0217979214501367 - 4. Xia, L., Jiang, G., Song, B. and Song, Y. (2016) Rumor Spreading Model Considering Hesitating Mechanism in Complex Social Networks. Physica A, 437, 295-303.
http://web.b.ebscohost.com/ehost/detail/detail?sid=69e62809-5fd9-402b-89f8-99f46c6df59a%40sessionmgr112&vid=0&hid=101&bdata=Jmxhbmc9emgtY24mc2l0ZT1laG9zdC1saXZl#AN=108506016&db=aph - 5. Watts, D.J. and Strogatz, S.H. (1998) Collective Dynamics of “Small-World” Networks. Nature, 393, 440-442.
http://www.nature.com/nature/journal/v393/n6684/full/393440a0.html - 6. Gabowski, A. and Kosinski, R.A. (2004) Epidemic Spreading in a Hierarchical Social Network. Physical Review E, 70, Article ID: 031908.
http://dx.doi.org/10.1103/PhysRevE.70.031908 - 7. Colizza, V., Barrat, A., Barthelemy, M. and Vespignani, A. (2007) Epidemic Predictability in Meta-Population Models with Heterogeneous Couplings: The Impact of Disease Parameter Values. International Journal of Bifurcation and Chaos, 17, 2491-2500.
http://dx.doi.org/10.1142/S0218127407018567 - 8. Li, H.L. (2013) Research on Multilayer Online Social Network Information Transmission Model. Shandong University of Finance and Economics, Jinan.
- 9. Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Dynamics and Endemic States in Complex Networks. Physical Review E, 63, Article ID: 066117.
http://dx.doi.org/10.1103/PhysRevE.63.066117 - 10. (2011) Sixty Years of Daily Newspaper Circulation Trends.
http://media-cmi.com/downloads/Sixty_Years_Daily_Newspaper_Circulation_Trends_050611.pdf - 11. (2016) Section 1: Watching, Reading and Listening to the News.
http://www.people-press.org/ - 12. (2015) Canada’s Population Estimates. Third Quarter 2015.
http://www.statcan.gc.ca/start-debut-eng.html
















