Journal of Applied Mathematics and Physics
Vol.03 No.12(2015), Article ID:61692,8 pages
10.4236/jamp.2015.312180
Thermal Properties and Phonon Dispersion of Bi2Te3 and CsBi4Te6 from First-Principles Calculations
Shen Li1, Clas Persson1,2
1Department of Materials Science and Engineering, Royal Institute of Technology, Stockholm, Sweden
2Department of Physics, University of Oslo, Oslo, Norway

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 29 October 2015; accepted 1 December 2015; published 4 December 2015

ABSTRACT
The narrow-gap semiconductor CsBi4Te6 is a promising material for low temperature thermoelectric applications. Its thermoelectric property is significantly better than the well-explored, high- performance thermoelectric material Bi2Te3 and related alloys. In this work, the thermal expansion and the heat capacity at constant pressure of CsBi4Te6 are determined within the quasiharmonic approximation within the density functional theory. Comparisons are made with available experimental data, as well as with calculated and measured data for Bi2Te3. The phonon band structures and the partial density of states are also investigated, and we find that both CsBi4Te6 and Bi2Te3 exhibit localized phonon states at low frequencies. At high temperatures, the decrease of the volume expansion with temperature indicates the potential of a good thermal conductivity in this temperature region.
Keywords:
Quasi Harmonic Approximation, Thermal Expansion, Heat Capacity, Phonon Dispersion

1. Introduction
In the recent years, thermoelectric (TE) materials have been studied extensively due to the advances in the material synthesis and an improved device performance [1] [2] . Special attention has been paid on searching for new compounds, alloys, and/or nanostructures with higher thermoelectric performance. The efficiency of the thermoelectric materials can be evaluated from the figure of merit ZT = (S2/rk)∙T where T is the absolute temperature; S is the Seebeck coefficient; r is the electrical resistivity; and k is the thermal conductivity. k has contribution from the electronic ke and the lattice thermal kL conductivities [3] . The power factor S2/r defines the characterized electrical properties. A good thermoelectric material shall typically exhibit low thermal conductivity and a large power factor. In the past years, many research groups have reported enhanced ZT in superlattices such as the Bi2Te3/Sb2Te3 systems, where the superlattice structures reduce the lattice thermal conductivity. Also, novel bulk and alloy compounds, such as antimony slivery telluride and its alloys with skutterudites, have shown improved ZT value which indicates that the materials can be suitable for thermoelectric applications. Bi2Te3 is already a well-established thermoelectric material at room temperature. Incorporating Cs in Bi2Te3 yields a somewhat more complex electronic structure, and this CsBi4Te6 compound is a potentially thermoelectric material with ZTmax = 0.8 at T = −23˚C, which thus is suitable for low temperatures.
All factors related to an optimized ZT are strongly influenced by the crystal structure, the electronic band structure, and the actual carrier concentration of the material. For the considered compounds (i.e., Bi2Te3 and CsBi4Te6) several investigations of the electronic structure and the electronic conductivity have been reported; see for instance Refs. [4] -[8] . The electronic part ke of the thermal conductivity can be calculated from the electronic structure through the Wiedemann-Franz relation ke = L0T/r (where L0 is the Lorenz number) but the corresponding lattice part kL cannot be calculated that easily. Analyzing the thermal properties makes it possible to at least better understand and describe the lattice part kL of thermal conductivity. In this study, we have therefore theoretically studied the thermal properties of Bi2Te3 and CsBi4Te6. We have computed the thermal expansions, the heat capacities at constant pressure, and the isothermal bulk moduli at finite temperatures; this can serve as a help to understand the underlying mechanism for the low kL for these two compounds. The computational study is based on the density functional theory (DFT) within the quasi harmonic approximation (QHA), which is known to provide reasonable good description of the thermal properties below the melting point of bulk materials [9] -[11] . The phonon frequencies in the first Brillouin zone are calculated by means of the density functional perturbation theory (DFPT). Recently, QHA based on DFPT has successfully been employed for several related materials, such as Ti3SiC2, Al3Mg, Al3Sc, and GaN [12] -[14] .
2. Computational Method
2.1. Theoretical Background
The most fundamental thermal properties of solids can be determined from the phonon dispersion ωq,v (for wave vector q of the vth mode) and the corresponding phonon density of states (DOS) as a function of frequency. The Helmholtz free energy at the temperature T and for a constant volume V is given by
 , where E0(V) is the ground state total energy at T = 0 K, Fph(V,T) is the vibration free energy from the phonon contribution, and Fel(V,T) is the free energy from the electronic excitations. From the phonon frequencies, the temperature dependent vibrational heat capacity CV at constant volume is determined through
, where E0(V) is the ground state total energy at T = 0 K, Fph(V,T) is the vibration free energy from the phonon contribution, and Fel(V,T) is the free energy from the electronic excitations. From the phonon frequencies, the temperature dependent vibrational heat capacity CV at constant volume is determined through
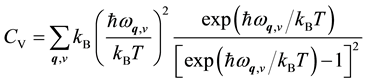 , (1)
, (1)
where kB is the Boltzmann’s constant. The thermal properties at constant pressure are analyzed from the free energy F(V,T). For a given temperature T, the equilibrium volume V0 is determined by minimizing the Gibbs free energy G(T,p) with respect to volume. This is utilized to further analyze the thermal properties, such as the thermal expansion ΔV/V0. The heat capacity at constant pressure is obtained from the derivative of G(T,p) as
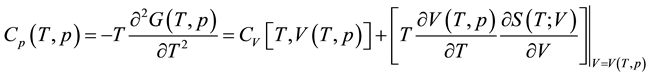 . (2)
. (2)
Here, S(T,p) is the entropy of the system and V(T,p) is the equilibrium volume at a specific pressure p and
temperature T. Moreover, the thermal expansion coefficient is given by , and the bulk modulus at zero pressure is given by
, and the bulk modulus at zero pressure is given by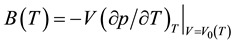 .
.
2.2. Computational Details
The computational study is based on the first-principles DFT approach as implement in the VASP program package [15] [16] , employing the projector augmented wave method (PAW) and using the Perdew-Burke-Ern- zerhof (PBE) exchange-correlation functional [17] . We fully relax the structure parameter and volume V0 of the primitive unit cell with a convergence of 10−5 eV/cell for the total energy, and 10−4 eV/Å for the forces on each atom. The energy cutoff was 500 eV. The k-space integration was performed with the tetrahedron method, involving a Γ-centered 10 × 10 × 10 k-mesh for Bi2Te3 and corresponding 4 × 4 × 4 k-mesh for the larger CsBi4Te6 compound. QHA was employed to compute the thermal properties at constant pressure. The thermodynamic functions were fitted to the integral form of Vinet’s equation of state (EOS) at zero pressure [18] . The Helmholtz free energy and the Gibbs free energy were obtained from the minimum values of the thermodynamic functions at finite temperatures, whereupon the equilibrium volume and the bulk moduli were obtained through the EOS. The heat capacity Cp (see, Equation (2)) was determined by a numerical differentiation ∂V/∂T and by polynomial fitting for both CV and S.
When calculating the phonon dispersion, we have employed the supercell approach and the force-constant method. The real space force constants of the supercells were calculated by the DFPT, whereupon the phonon modes were calculated from the force constants using the PHONOPY package [19] . Here, the phonon dispersions and the phonon DOS were calculated with a 2 × 2 × 2 supercell for Bi2Te3 and a 1 × 1 × 2 supercell for CsBi4Te6, which implies 40 atoms and 88 atoms, respectively. In those calculations, 41 × 41 × 41 Monkhorst- Pack grids were used which is expected to be sufficient to avoid the mean relative error of the DOS.
3. Results
3.1. Crystal Structure
Bi2Te3 is a semiconductor with a narrow band gap. Although its primitive unit cell has rhombohedral symmetry with the space group , the crystal structure is usually described by hexagonal coordinates. With a hexagonal unit cell [see Figure 1(a)], there are five layers consisting of Te(1)-Bi-Te(2)-Bi-Te(1) chains along the hexagonal axis. From our relaxation, we find that the calculated average bond length of Te-Te, Bi-Te(1), and Bi-Te(2) are 3.60, 3.06, and 3.22 Å, respectively. The crystalline structure of CsBi4Te6 is related to that of Bi4Te6, however it crystallizes with the space group C2/m; see Figure 1(b). The layered structure of CsBi4Te6 is composed by infinitely long anionic [Bi4Te6]− blocks with the Cs+ ions reside between the anionic layers. The [Bi4Te6]− blocks can be seen as fragments of NaCl-like lattices, and each block is a two-Bi octahedral thick and four-Bi octahedral wide in the ac-plane while infinitely along the b-axis. The compound can be considered as a one-dimensional like
, the crystal structure is usually described by hexagonal coordinates. With a hexagonal unit cell [see Figure 1(a)], there are five layers consisting of Te(1)-Bi-Te(2)-Bi-Te(1) chains along the hexagonal axis. From our relaxation, we find that the calculated average bond length of Te-Te, Bi-Te(1), and Bi-Te(2) are 3.60, 3.06, and 3.22 Å, respectively. The crystalline structure of CsBi4Te6 is related to that of Bi4Te6, however it crystallizes with the space group C2/m; see Figure 1(b). The layered structure of CsBi4Te6 is composed by infinitely long anionic [Bi4Te6]− blocks with the Cs+ ions reside between the anionic layers. The [Bi4Te6]− blocks can be seen as fragments of NaCl-like lattices, and each block is a two-Bi octahedral thick and four-Bi octahedral wide in the ac-plane while infinitely along the b-axis. The compound can be considered as a one-dimensional like


Figure 1. Crystal structure of (a) hexagonal layered Bi2Te3 and (b) CsBi4Te6. The layered structure of CsBi4Te6 is composed of anionic, infinitely long [Bi4Te6]− blocks where the Cs+ ions are located between two anionic blocks. The main Bi-Bi bond in CsBi4Te6 is indicated by the arrow.
crystal structure, and therefore the structure is strongly anisotropic. CsBi4Te6 can be regarded as a reduced structure of Bi2Te3. From comparing the crystal structure of CsBi4Te6 and Bi4Te6 = 2(Bi2Te3) one finds that the additional electron per two formula units of Bi2Te3 implies a complete reorganization of the Bi2Te3 framework. Thereby, the extra valence electrons in CsBi4Te6 localize on the Bi atoms which leads to a new formation along the a-axis with Bi-Bi bonds. Our calculated length of this Bi-Bi bond in CsBi4Te6 is 3.23 Å, which is thus close to the bond length of Bi-Te(2) in Bi2Te3.
3.2. Thermal Expansion, Bulk Modulus, and Heat Capacities
Table 1 summarizes the volume expansion ΔV/V0, thermal expansion coefficient a, as well as the heat capacities Cp and CV of Bi2Te3 and CsBi4Te6; we present the results for the temperatures T = 300 and 600 K. The temperature dependence of the volume expansion for T = 0 - 900 K are shown in Figure 2. The volume expansion is defined as ΔV/V0, with ΔV = V − V0 and where V0 is the corresponding volume at T = 300 K, and by definition ΔV/V0 is negative below this 300 K. The volume expansions of the two considered compounds have almost the same linear increase at low temperature (in the region 50 - 300 K), but this consistency disappeared for higher temperatures. This is obvious for temperatures above 400 K where Bi2Te3 has somewhat larger volume expansion than CsBi4Te6.
Figure 3 displays the thermal expansion coefficient
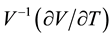 of Bi2Te3 and CsBi4Te6. The results reveal that the thermal expansion increases considerably with increasing temperatures in the low temperature region below 170 K. In this region the two compounds have almost equivalent thermal expansion, which is in agreement with similar volume expansions for low temperatures. Moreover, the expansion coefficient reaches a maximum value of roughly 55 × 10−5 K−1 for both Bi2Te3 (maximum at T ~ 300 K) and CsBi4Te6 (at T ~ 150 K). For higher
of Bi2Te3 and CsBi4Te6. The results reveal that the thermal expansion increases considerably with increasing temperatures in the low temperature region below 170 K. In this region the two compounds have almost equivalent thermal expansion, which is in agreement with similar volume expansions for low temperatures. Moreover, the expansion coefficient reaches a maximum value of roughly 55 × 10−5 K−1 for both Bi2Te3 (maximum at T ~ 300 K) and CsBi4Te6 (at T ~ 150 K). For higher
Table 1. The volume expansion ΔV/V0, the thermal expansion coefficient a, and the heat capacities Cp and CV of Bi2Te3 and CsBi4Te6 at the temperatures T = 300 and 600 K. The unit J∙mol−1∙K−1 for the heat capacities refers to formula unit cell: 40 atoms for Bi2Te3 and 88 atoms for CsBi4Te6.
Figure 2. Relative volume expansion ΔV/V0 as a function of temperature T, where V0 is the corresponding volume at T = 300 K (figure caption).
Figure 3. Thermal expansion coefficient α of Bi2Te3 and CsBi4Te6 as function of temperature. The dashed line indicates the temperature T = 230 K where the expansion coefficients are equal for the two compounds.
temperatures, the thermal expansion of Bi2Te3 is significantly larger than that of CsBi4Te6. Moreover, whereas the expansion coefficient of Bi2Te3 tends to be rather stable at ~(50 - 55) × 10−5 K−1 for high temperatures, the corresponding coefficient of CsBi4Te6 drops almost linearly to about half its maximum value, that is, from ~57 × 10−5 K−1 to ~28 × 10−5 K−1 at T = 900 K.
It is noticeable that for many similar compounds the thermal expansion coefficient is increasing with increasing temperature. However, for Bi2Te3 we thus find a rather constant (and slightly decreasing) expansion coefficient, and for CsBi4Te6, we observe a strong decrease of the expansion coefficient in the high temperature region. This is a direct consequence of the decrease of the volume expansion slope for large T for CsBi4Te6; see Figure 2.
The bulk modulus is determined from the EOS calculation, and the resulting values for T = 0 K are B0 = 47.8 GPa for Bi2Te3 and 37.8 GPa for CsBi4Te6. Thus, we find that the bulk modulus of Bi2Te3 is about 25% larger than that of CsBi4Te6.
The heat capacities CV and Cp are investigated directly from the phonon frequency dispersion using the QHA approach, and the resulting CV and Cp for Bi2Te3 and CsBi4Te6 are presented in Figure 4. We find that the two compounds have very similar heat capacities. Cp is roughly 3% - 4% larger than CV at T = 300 K and 4% - 7% larger at T = 600 K (Table 1). Moreover, Cp and CV for both Bi2Te3 and CsBi4Te6 obey the law of T3 behavior at low temperatures. At high temperatures however, CV reaches a constant value which is approximately given by the classic equipartition law
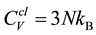 where N is the number of atoms of the considered system. Here, N = 5 for Bi2Te3 and 11 for CsBi4Te6, yielding
where N is the number of atoms of the considered system. Here, N = 5 for Bi2Te3 and 11 for CsBi4Te6, yielding
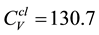 and 281.2 J∙mol−1∙K−1, respectively, in the classical limit. At ambient pressure and at room temperature T = 300 K, the calculated value of Cp for Bi2Te3 is 126 J∙mol−1∙K−1 (Table 1) which agree with the experimental data 126 J∙mol−1∙K−1 [20] [21] . We find also that the calculated results fit very well with the experimental data [20] [21] in the whole low temperature region apart from the measure data point for the lowest temperature; see Figure 4. The corresponding calculated Cp value at T = 300 K for CsBi4Te6 is 280 J∙mol−1∙K−1. This is roughly twice as large value compared with Bi2Te3, and the reason is that the unit cell of CsBi4Te6 contains roughly twice as many atoms (88 atoms) as in the unit cell of Bi2Te3 (40 atoms) and the mol−1 describes formula unit cell. In the units of J∙kg−1∙K−1, the corresponding value is Cp = 391 J∙kg−1∙K−1 for Bi2Te3 and 400 J∙kg−1∙K−1 for CsBi4Te6.
and 281.2 J∙mol−1∙K−1, respectively, in the classical limit. At ambient pressure and at room temperature T = 300 K, the calculated value of Cp for Bi2Te3 is 126 J∙mol−1∙K−1 (Table 1) which agree with the experimental data 126 J∙mol−1∙K−1 [20] [21] . We find also that the calculated results fit very well with the experimental data [20] [21] in the whole low temperature region apart from the measure data point for the lowest temperature; see Figure 4. The corresponding calculated Cp value at T = 300 K for CsBi4Te6 is 280 J∙mol−1∙K−1. This is roughly twice as large value compared with Bi2Te3, and the reason is that the unit cell of CsBi4Te6 contains roughly twice as many atoms (88 atoms) as in the unit cell of Bi2Te3 (40 atoms) and the mol−1 describes formula unit cell. In the units of J∙kg−1∙K−1, the corresponding value is Cp = 391 J∙kg−1∙K−1 for Bi2Te3 and 400 J∙kg−1∙K−1 for CsBi4Te6.
3.3. Phonon Dispersion and Phonon Density of States
The dispersion curves for Bi2Te3 and CsBi4Te6 are shown along the high symmetry directions in their respective Brillouin zones (Figure 5). For Bi2Te3, the atom-resolved DOS reveals that the phonon states in the lower energy
Figure 4. The heat capacity at constant pressure Cp and the heat capacity at constant volume CV as functions of temperature. The curves of CV follow roughly the T3-law at low temperature and tend to be fairly constant at higher temperatures. Here, the unit J∙mol−1∙K−1 refers to formula unit cell, and due to a larger unit cell the values of the heat capacity of CsBi4Te6 is about 2.2 times larger than of Bi2Te3.

Figure 5. Phonon band structure and its corresponding total and atomic-resolved DOS of (a) Bi2Te3 and (b) CsBi4Te6. The difference in the frequency at the Brillouin zone edge (1.12 THz for Bi2Te3 whereas 0.76 THz for CsBi4Te6) is due to the Cs atoms in CsBi4Te6 which have atomic mass between that of Bi and Te. The CsBi4Te6 structure implies also the presence of Bi-Bi bond (see Figure 1).
region compose mainly of Bi-like states, while Te-like states contribute more in the higher energy region since the atomic mass of Te is significantly lighter than that of Bi.
When comparing the phonon dispersions of atomic-resolved DOS of Bi2Te3 [Figure 5(a)] with CsBi4Te6 [Figure 5(b)], it is clear the shapes of the dispersions and DOS of Bi2Te3 and CsBi4Te6 shows both similarities and differences. The flat regions of phonon dispersion curves in Bi2Te3 lead to two main peaks in the atom-re- solved DOS indicating localizations of states that behave as the “atomic states” for Bi and Te atoms, respectively. Similar atom-like characters were also found in the atom-resolved DOS of CsBi4Te6 for the Cs and Te atoms, whereas the Bi atoms show more delocalization in CsBi4Te6 because the Bi-Bi bonds are influenced by the Cs+.
The acoustic modes in Bi2Te3 are rather disperse up to 1.12 THz and they depend primarily the Bi atoms, while the acoustic modes in CsBi4Te6 are disperse up to 0.76 THz and involve mainly contribution from the Cs atoms. It has been discussed that the low frequency phonons as a function of temperature play an important role in the thermal expansion [22] .
In Bi2Te3, the phonon dispersion with frequencies lower than 1.7 THz is a mixture between acoustic and optical modes, and these phonons contribute significantly to the thermal expansion below 300 K. CsBi4Te6 on the other hand, shows relatively delocalized states in the whole phonon dispersion curve because the Cs atom is rather different from Bi. The differences in the phonon vibration modes are mainly due to the different crystal symmetry and the distribution of atom mass in Bi2Te3 and CsBi4Te6, which also lead to the different in the thermal expansions as shown in Figure 3.
4. Conclusion
In this work, the thermal properties and the phonon dispersions of Bi2Te3 and CsBi4Te6 have been calculated, employing the DFT and the DFPT within the quasi-harmonic approximation. The volume expansions of these two compounds have similar linear increase for temperatures below 300 K, and Bi2Te3 has slightly larger volume expansion than CsBi4Te6 for temperatures above 300 K. However, both compounds show a decrease of the volume expansion in the high temperature region. For Bi2Te3 the calculated value of Cp is 126 J∙mol−1∙K−1 at ambient pressure and room temperature which supports the experimental data. From the calculated phonon dispersion and phonon DOS, we conclude that CsBi4Te6 has relatively delocalized states in the phonon dispersion curve due to the Cs atomic mass which is between those of Bi and Te.
Acknowledgements
This work is supported by the European EM-ECW scholarship program Tandem, the Swedish Energy Agency, and the Swedish Research Council. C.P. acknowledges support from the Research Council of Norway (contracts No. 228854 and 221469). We acknowledge access to the high-performance computing resources at the NSC and HPC2N centers through SNIC and Matter network.
Cite this paper
ShenLi,ClasPersson, (2015) Thermal Properties and Phonon Dispersion of Bi2Te3 and CsBi4Te6 from First-Principles Calculations. Journal of Applied Mathematics and Physics,03,1563-1570. doi: 10.4236/jamp.2015.312180
References
- 1. Chung, D.Y., Hogan, T., Brazis, P., Rocci-Lane, M., Kannewurf, C., Bastea, M., Uher, C. and Kanatzidis, M.G. (2000) CsBi4Te6: A High-Performance Thermoelectric Material for Low-Temperature Applications. Science, 287, 1024.
http://dx.doi.org/10.1126/science.287.5455.1024 - 2. Youn, S.J. and Freeman, A.J. (2001) First-Principles Electronic Structure and Its Relation to Thermoelectric Properties of Bi2Te3. Physical Review B, 63, Article ID: 085112.
http://dx.doi.org/10.1103/PhysRevB.63.085112 - 3. Tritt, T.M. (1999) Holey and Unholey Semiconductors. Science, 283, 804.
http://dx.doi.org/10.1126/science.283.5403.804 - 4. Sofo, J.O. and Mahan, G.D. (1998) Electronic Structure of CoSb3: A Narrow-Band-Gap Semiconductor. Physical Review B, 58, 15620.
http://dx.doi.org/10.1103/PhysRevB.58.15620 - 5. Bell, L.E. (2008) Cooling, Heating, Generating Power, and Recovering Waste Heat with Thermoelectric Systems. Science, 321, 1457.
http://dx.doi.org/10.1126/science.1158899 - 6. Katsuki, S. (1969) The Band Structure of Bismuth Telluride. Journal of the Physical Society of Japan, 26, 58.
http://dx.doi.org/10.1143/JPSJ.26.58 - 7. Larson, P., Mahanti, S.D., Chung, D.-Y. and Kanatzidis, M.G. (2002) Electronic Structure of CsBi4Te6: A High-Performance Thermoelectric at Low Temperatures. Physical Review B, 65, 45205.
http://dx.doi.org/10.1103/PhysRevB.65.045205 - 8. Lykke, L., Iversen, B.B. and Madesen, G.K.H. (2006) Electronic Structure and Transport in the Low-Temperature Thermoelectric CsBi4Te6: Semiclassical Transport Equations. Physical Review B, 73, Article ID: 195121.
http://dx.doi.org/10.1103/PhysRevB.73.195121 - 9. Biernacki, S. and Scheffler, M. (1989) Negative Thermal Expansion of Diamond and Zinc-Blende Semiconductors. Physical Review Letters, 63, 290.
http://dx.doi.org/10.1103/PhysRevLett.63.290 - 10. Pavone, P., Karch, K., Schutt, O., Strauch, D., Windl, W., Giannozzi, P. and Baroni S. (1993) Ab Initio Lattice Dynamics of Diamond. Physical Review B, 48, 3156.
http://dx.doi.org/10.1103/PhysRevB.48.3156 - 11. Nie, Y.Z. and Xie, Y.Q. (2007) Ab Initio Thermodynamics of the HCP Metals Mg, Ti, and Zr. Physical Review B, 75, Article ID: 174117.
http://dx.doi.org/10.1103/PhysRevB.75.174117 - 12. Togo, A., Chaput, L., Tanaka, I. and Hug, G. (2010) First-Principles Phonon Calculations of Thermal Expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2. Physical Review B, 81, Article ID: 174301.
http://dx.doi.org/10.1103/PhysRevB.81.174301 - 13. Li, D.-L., Chen, P., Yi, J.-X., Tang, B.-Y., Peng, L.-M. and Ding, W.-J. (2009) Ab Initio Study on the Thermal Properties of the FCC Al3Mg and Al3Sc Alloys. Journal of Physics D: Applied Physics, 42, Article ID: 225407.
http://dx.doi.org/10.1088/0022-3727/42/22/225407 - 14. Xu, L.-C., Wang, R.-Z., Yang, X.-D. and Yan, H. (2011) Thermal Expansions in Wurtzite AlN, GaN, and InN: First-Principle Phonon Calculations. Journal of Applied Physics, 110, Article ID: 043528.
http://dx.doi.org/10.1063/1.3627237 - 15. Kresse, G. and Hafner, J. (1993) Ab Initio Molecular Dynamics for Liquid Metals. Physical Review B, 47, 558-561.
http://dx.doi.org/10.1103/PhysRevB.47.558 - 16. Kresse, G. and Furthmüller, J. (1996) Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Physical Review B, 54, 11169-11186.
http://dx.doi.org/10.1103/PhysRevB.54.11169 - 17. Perdew, J.P., Burke, K. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 77, 3865-3868.
http://dx.doi.org/10.1103/PhysRevLett.77.3865 - 18. Vinet, P., Rose, J.H., Ferrante, J. and Smith, J.R. (1989) Universal Features of the Equation of State of Solids. Journal of Physics: Condensed Matter, 1, 1941-1963.
http://dx.doi.org/10.1088/0953-8984/1/11/002 - 19. Togo, A., Oba, F. and Tanaka, I. (2008) First-Principles Calculations of the Ferroelastic Transition between Rutile-Type and CaCl2-Type SiO2 at High Pressures. Physical Review B, 78, Article ID: 134106.
http://dx.doi.org/10.1103/PhysRevB.78.134106 - 20. Pavlova, L.M., Shtern, Y.I. and Mironov, R.E. (2011) Thermal Expansion of Bismuth Telluride. High Temperature, 49, 369-379.
http://dx.doi.org/10.1134/S0018151X1103014X - 21. Gorbachuk, N.P., Bolgar, A.S., Sidorko, V.R. and Goncharuk, L.V. (2004) Heat Capacity and Enthalpy of Bi2Si3 and Bi2Te3 in the Temperature Range 58-1012 K. Powder Metallurgy and Metal Ceramics, 43, 284-290.
http://dx.doi.org/10.1023/B:PMMC.0000042464.28118.a3 - 22. Zwanziger, J.W. (2007) Phonon Dispersion and Grüneisen Parameters of Zinc Dicyanide and Cadmium Dicyanide from First Principles: Origin of Negative Thermal Expansion. Physical Review B, 76, Article ID: 052102.
http://dx.doi.org/10.1103/physrevb.76.052102






