Received 24 June 2015; accepted 1 September 2015; published 4 September 2015

ABSTRACT

Topological methods are rapidly developing and are becoming more used in physics, biology and chemistry. One area of topology has showed its immense potential in explaining potential financial contagion and financial crisis in financial markets. The aforementioned method is knot theory. The movement of stock price has been marked and braids and knots have been noted. By analysing the knots and braids using Jones polynomial, it is tried to find if there exists an untrivial knot equal to unknot? After thorough analysis, possible financial contagion and financial crisis prediction are analysed by using instruments of knot theory pertaining in that sense to Jones, Laurent and Alexander polynomial. It is proved that it is possible to predict financial disruptions by observing possible knots in the graphs and finding appropriate polynomials. In order to analyse knot formation, the following approach is used: “Knot formation in three-dimensional space is considered and the equations about knot forming and its disentangling are considered”. After having defined the equations in three-dimensional space, the definition of Brownian bridge concerning formation of knots in three-dimensional space is defined. Using analogy method, the notion of Brownian bridge is translated into 2-dimensional space and the foundations for the application of knot theory in 2-dimensional space have been set up. At the same time, the aforementioned approach is innovative and it could be used in accordance with stochastic analysis and quantum finance.

Keywords:

Topology, Knot Theory, Financial Markets, Stochastic Analysis, Financial Disruption, Financial Crisis, Topology, Knots, Braids

1. Introduction

In this paper, random dynamical systems are considered. It is assumed that financial time series exhibit fractional Brownian motion and knot theory is used in order to analyse the formation of knots in financial time series. The foundations are set up to further the analysis of the financial time series using quantum physics, knot theory and topology. Firstly, we will define mathematically random system, afterwards Wiener process via stochastic differential equation is defined and ordinary Brownian motion is at the same time defined. As ordinary Brownian motion is a subclass of fractional Brownian motion, fractional Brownian motion is explained. In the theory section, one question was posed and it stated: “What would happen if the time series pertaining in that sense to major financial indices follow fractional Brownian motion and are forming knots? Can the financial crisis be predicted by observing knot formation?” Afterwards, we proceed to analysis and formation of knots in three- dimensional space, we present the equations that represent the formation of 3 dimensional knots by using for- mulas from quantum physics and afterwards and we make the Brownian bridge hypothesis in three-dimensional space and translate it to two-dimensional space. With the aforementioned, thesis for analysis of two-dimensional knot set-up is defined and hopeful. The following papers of the author will approach the further analysis and development of equations in the formation of knots in two-dimensional space.

2. Theoretical Background

Random dynamical system [1] is a dynamical system in which the equations of motion have an element of randomness to them. State space 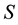and a set of maps from 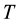to 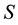can be considered as the set of all possible equations of motion and a probability distribution 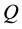on the set 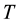that represents the random choice of map should is also considered. Motion in a random dynamical system can be informally thought of as a state 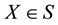evolving according to a succession of maps randomly chosen according to distribution Q.

If we want to implement a solution to stochastic differential equation, firstly some definitions should be set-up:

Let 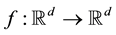be a d-dimension vector field and let. Suppose that the solution to the stochastic differential equation

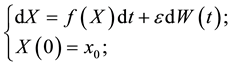(1)

exists for all positive time and some (small) interval of negative time dependent upon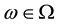, where denotes a d-dimensional Wiener process. Implicitly, this statement uses the classical Wiener probability space:

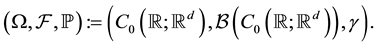(2)

In this context, the Wiener process is the coordinate process.

Now define a flow map or (solution operator) [2] 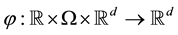by

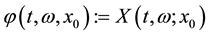(3)

Then, (or, more precisely, the pair) is a (local, left-sided) random dynamical system. The process of generating a “flow” from the solution to a stochastic differential equation leads us to study suitably defined “flows” on their own. These “flows” are random dynamical systems.

Components of a random dynamical system [3] are comprised of a base flow, the noise and a cocycle dynamical system on the physical space.

Let be a probability space, the noise space. If the base flow is defined as follows: for each ‘time’ and a measure-preserving function be defined.

Assume the following:

1) , the identity function on;

2) For all,.

That is forms a group of measure-preserving transformation of the noise. For one- sided random dynamical systems, only positive indices are considered.

Now let be a complete separable metric space, the phase space. Let be a -measurable function:

For all, the identity function on;

For all is a continuous in both and;

satisfies the cocycle property, for almost all

(4)

In case, we are considering a random dynamical system driven by Wiener process, the base flow would be given by:

(5)

This says that starts the noise at time instead of time 0. Thus the cocycle property can be read as saying that evolving the initial condition with some noise for seconds and then through seconds with same noise gives the same result as evolving through with that same noise.

Fractional Brownian Motion

The fBm is an extension of the classical Brownian motion that allows its disjoint increments to be correlated. Fractional Brownian motion is not Markovian and this becomes a strong difficulty to study and put the model into practice.

A centered Gaussian process is called a fractional Brownian motion (fBm) with Hurst parameter if it has the covariance function:

(6)

Usually it is assumed that. If, is not a semimartingale.

(7)

If, disjoint increments are positively correlated.

(8)

If, disjoint increments are negatively correlated:

(9)

-is Holder continuous, for every

The main question that is posed what would happen if the time series pertaining in that sense to major financial indices follow fractional Brownian motion and are forming knots? Can the financial crisis be predicted by observing knot formation?

3. Theoretical Conclusions and Results

Conjecture 1: (Frisch-Wasserman Delbruck (FWD) Conjecture) [4] The probability that a randomly embedded circle of length in is knotted tends to one as tends to infinity.

The probability to find a closed N-step random walk in in some prescribed topological state can be presented in the following way [4] :

(10)

where is the probability to find th step of the trajectory in the point if jth step is in and

is the functional representation of the knot invariant corresponding to the trajectory with bond coordinates.

In three-dimensional space, the following expression is found for [1] :

(11)

Introducing the time, , along the trajectory we rewrite the distribution function in the path integral form with the Wiener measure density [2] :

(12)

If phase trajectories can be mutually transformed by means of continuous deformations, then the summation should be extended to all available paths in the system but if the phase space consists of different topological domains, then the summation in the above equation refers to the paths from the exclusively defined class and knot entropy problem arises [5] .

The 2D version of the Edward’s model is formulated as follows. Take a plane with an excluded origin, producing the topological constraint for the random walk of length L with the initial and final points and respectively. The trajectory makes n turns around the origin, but as we want to use so how to calculate the distribution function

In the said model, the state C is fully characterised by number of turns of the path around the origin. The corresponding abelian topological invariant is known as Gauss linking number and when represented in the contour integral form, reads [6] :

(13)

where

(14)

And is angle distance between the ends of random walk.

Using the Fourier transform of the -function we arrive at by substituting Equation (23) into Equation (20)

(15)

We introduce the entropic force:

(16)

Which acts on the closed chain when the distance between the obstacle and a certain point of the trajectory changes. Apparently the topological constraint leads to the strong attraction of the path to the obstacle for any and to the weak repulsion for.

Distribution function for the random walk with the fixed ends and specific algebraic area S.

Therefore according to D. S. Khandekar and F. W. Wiegel again represented the distribution function in terms of the path integral (Equation (20) with the replacement:

(17)

where the is written in the Landau gauge [7] [8] ):

(18)

The final distribution function reads to [1] :

(19)

where

(20)

And (21)

There is no principal difference between the problems of random walk statistics in the presence of a single topological obstacle or with a fixed algebraic area-both of them have the “abelian” nature.

The principal difficulty connected with application of the Gauss invariant is due to its incompleteness.

Any closed path on can be represented by the “word” consisting of set of letters. Taking

into account the word can be reduced to the minimal irreducible representation. It is easy to understand that the word represents only the irreducible representation. The non-abelian character of the topological constraints is reflected in the fact that different entanglements do not commute:.

Application of Gauss invariant is due to its incompleteness. It has been recognized that the Alexander polynomials [9] being much stronger invariants than the Gauss linking number, is a good for calculation of entangled random walks.

The probability to find a randomly generated knot in a specific topological state. Take an arbitrary graph and assume the following theorem: Two knots embedded in can be deformed continuously one into the other if and only if the diagram of one knot can be transformed into the diagram corresponding to another knot via the sequence of simple local moves of type I, II and shown in figure below.

Two knots are called regular isotopic if they are isotopic with respect to two last Reidemeister moves(II and III); meanwhile, if they are isotopic with respect to all moves, they are called ambient isotopic. As it can be seen from Figure 1, the Reidemeister move of type I leads to the cusp creation on the projection. At the same time it should be noted that all real 3D-knots (links) are of ambient isotopy.

Now, after the Reidemeister theorem has been formulated, it is possible to describe the construction of polynomial “bracket” invariant in the way proposed by L. H. Kauffman [10] .

For the knot diagram with N vertices there are different microstates, each of them representing the set of splittings of all N vertices. The entire microstate, , corresponds to the knot (link) disintegration to the system of disjoint and non-selfintersecting circles. The number of such circles for the given microstate we denote as.

Completed by intial condition:

, K is not empty

where O denotes the separation of trivial loop.

Actually, the knot structure is formed during the random closure of the path and cannot be changed without the path rupture.

Figure 2 presents the probability of knot formation. It presents that the highest probability of knot formation is for specific value of which minimizes the free energy of associated Potts system. As we become more specific, probability of knot formation decreases.

Knot complexity, the power of some algebraic invariant [11] :

(22)

One and the same value of characterizes a narrow class of “topologically similar” knots which is, however, much broader than the class represented by the polynomial invariant. This makes it possible to introduce the smoothed measures and distribution functions for.

Take a set of knots obtained by closure of -braids of length with the uniform distribution over the generators. The conditional probability distribution for the normalized complexity of Al- exander polynomial invariant has the Gaussian behavior and is given by [12] :

(23)

Actually, the conditional probability distribution that the random walk on the backbone graph,

, starting in the origin, visits after first () steps some graph vertex situated at the distance

and after step returns to the origin, is determined as follows:

(24)

Recall that the distribution function for the free random walk in D-dimensional Euclidean space obeys the standard heat equation [1] :

(25)

With the diffusion coefficient and appropriate initial and normalization conditions:

(26)

(27)

The diffusion equation for the scalar density of the free random walk on a Riemann manifold reads

(28)

where

(29)

(30)

And where is the metric tensor of the manifold.

3D space:

The Brownian brigde condition for random walks in space of constant negative curvature makes the space “effectively flat” turning the corresponding limit probability distribution for random walks to the ordinary central limit distribution.

This question is valid in Euclidean space. If we translate it into two-dimensional space, the following result is obtained:

The Brownian bridge condition for random walks in 2-dimensional space makes the corresponding limit probability distribution for random walks to the ordinary central limit distribution.

4. Conclusion

The above mentioned equations have set up the foundations of applying knot theory to financial time series analysis. Firstly, the set-up for forming knots in three-dimensional space was performed using quantum physics tools and afterwards the set-up was translated into the 2-dimensional space. Brownian bridge was defined in and. The equations given have made it possible how the knots are formed in two-dimensional space as well as in three-dimensional space. At the same time, the hypothesis for Brownian bridge in 2-dimensional space is the basics for knot theory analysis in 2-dimensional space.

Acknowledgements

I would like to thank my family for the support, especially my father, mother, sister and aunt.

Cite this paper

OgnjenVukovic, (2015) Predicting Financial Contagion and Crisis by Using Jones, Alexander Polynomial and Knot Theory. Journal of Applied Mathematics and Physics,03,1073-1079. doi: 10.4236/jamp.2015.39133

References