Journal of Applied Mathematics and Physics
Vol.03 No.03(2015), Article ID:54903,5 pages
10.4236/jamp.2015.33041
Classifying Exact Traveling Wave Solutions to the Coupled-Higgs Equation
Jiying Liu
School of Mathematics and Statistics, Northeast Petroleum University, Daqing, China
Email: liujiying216@126.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2015; accepted 18 March 2015; published 23 March 2015
ABSTRACT
By the complete discrimination system for polynomials, we classify exact traveling wave solutions to the Coupled-Higgs Equation.
Keywords:
Traveling Wave Solution, Complete Discrimination System for Polynomials, The Coupled-Higgs Equation

1. Introduction
There are many methods to study the exact traveling wave solutions of the nonlinear differential Equations, such as the inverse scattering method [1] , Jacobi elliptic function expansion method [2] , homogeneous balance method [3] , 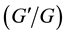 -expansion method [4] , and so on. At the same time, Liu [5] introduced the complete discrimination system method to give the classification of exact traveling wave solutions to some nonlinear equations, the method is simple and efficient. Using this method, some new traveling wave solutions were obtained to the Zhiber-Shabat Equation [6] .
-expansion method [4] , and so on. At the same time, Liu [5] introduced the complete discrimination system method to give the classification of exact traveling wave solutions to some nonlinear equations, the method is simple and efficient. Using this method, some new traveling wave solutions were obtained to the Zhiber-Shabat Equation [6] .
In this paper, we focus on the Coupled-Higgs Equation to classify its traveling wave solutions. A. Jabbari et al. [4] have got some traveling wave solutions to the Coupled-Higgs Equation. By Liu’s method, we’ll classify exact traveling wave solutions to the Coupled-Higgs Equation.
2. The Traveling Wave Solutions to the Coupled-Higgs Equation
The Coupled-Higgs Equation reads as
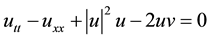 , (1)
, (1)
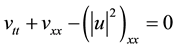 . (2)
. (2)
We introduce transformation as follows
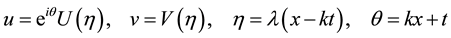 . (3)
. (3)
Substituting Equation (3) into Equation (1) and Equation (2) yields nonlinear ordinary differential equation as follows
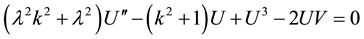 , (4)
, (4)
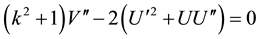 . (5)
. (5)
Integrating Equation (5) twice with respect to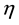 , and setting the integration constant to zero yields
, and setting the integration constant to zero yields
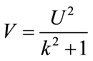 . (6)
. (6)
Substituting Equation (6) into Equation (4) yields the following nonlinear ordinary difference equation
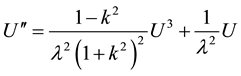 . (7)
. (7)
Integrating Equation (7) once with respect to 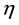 yields
yields
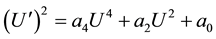 , (8)
, (8)
where
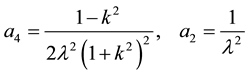 , (9)
, (9)
and  is an arbitrary constant.
is an arbitrary constant.
In order to find the traveling wave solutions to Equation (1) and Equation (2), let us solve Equation (8). In this article, there are two cases to discuss the exact solutions of Equation (8) according to the coefficient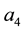 .
.
Case 2.1. When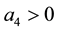 , we take the transformation as follows
, we take the transformation as follows
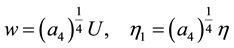 . (10)
. (10)
Substituting (10) into (8) yields

where

In order to obtain the solutions to Equation (11), we let

Substituting (13) into (11) yields

Furthermore, integrating Equation (14), we have

where

and 



Case 2.1.1.



If

Case 2.1.2.




Case 2.1.3.








When

where
Case 2.1.4.


where
Case 2.2. When

Substituting (23) into (8) yields

where

In order to obtain the solutions to Equation (24), we let

Substituting (26) into (24) yields

Furthermore, integrating Equation (27), we have

where

And 



Case 2.2.1.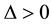

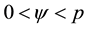

Case 2.2.2.

From the above we know that Equations (17)-(22) and (30) are all possible solutions of Equations (15) and (28). According to Equations (13), (10), (6), (3) and (26), (23), (6), (3), we can give the classification of all single traveling wave solutions to the Coupled-Higgs Equation with respective parameter conditions as follows:














3. Conclusion
By the complete discrimination system for polynomial method, we have obtained the classification of traveling wave solutions to the Coupled-Higgs Equation. These solutions include triangle periodic solutions, rational func- tion solution, Jacobi elliptic function periodic solutions, and so on. This method is simple and efficient.
References
- Ablowitz, M.J. and Clarkson, P.A. (1991) Solitons, Non-Linear Evolution Equations and Inverse Scattering Transform. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511623998
- Xiang, C.H. (2011) Jacobi Elliptic Function Solutions for (2 + 1) Dimensional Boussinesq and Kadomtsev-Petviashvili Equation. Applied Mathematics, 2, 1313-1316. http://dx.doi.org/10.4236/am.2011.211183
- Khalfallah, M. (2008) Exact Traveling Wave Solutions of the Boussinesq-Burgers Equation. Mathematical and Computer Modelling, 49, 666-671. http://dx.doi.org/10.1016/j.mcm.2008.08.004
- Jabbari, A., Kheiri, H. and Bekir, A. (2011) Exact Solutions of the Coupled Higgs Equation and the Maccari System Using He’s Semi-Inverse Method and (G’/G)-Expansion Method. Computers and Mathematics with Applications, 62, 2177-2186. http://dx.doi.org/10.1016/j.camwa.2011.07.003
- Liu, C.S. (2010) Applications of Complete Discrimination System for Polynomial for Classifications of Traveling Wave Solutions to Nonlinear Differential Equations. Computer Physics Communications, 181, 317-324. http://dx.doi.org/10.1016/j.cpc.2009.10.006
- Wang, C.Y. and Du, X.H. (2013) Classifying Traveling Wave Solutions to the Zhiber-Shabat Equation. Journal of Applied Mathematics and Physics, 1, 1-3. http://dx.doi.org/10.4236/jamp.2013.12001

