Journal of Applied Mathematics and Physics Vol.02 No.13(2014),
Article ID:52433,9 pages
10.4236/jamp.2014.213133
Multifractal Analysis of the Asympyotically Additive Potentials
Lan Xu1, Long Yang2
1Department of Mathematics and Physics, Suzhou Vocational University, Suzhou, China
2Department of Mathematics, Soochow University, Suzhou, China
Email: jssvcxulan@gmail.com, soochowyl@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 September 2014; revised 15 October 2014; accepted 21 October 2014
ABSTRACT
Multifractal analysis studies level sets of asymptotically defined quantities in
dynamical systems. In this paper, we consider the
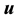 -dimension spectra on such
level sets and establish a conditional variational principle for general asymptotically
additive potentials by requiring only existence and uniqueness of equilibrium states
for a dense subspace of potential functions.
-dimension spectra on such
level sets and establish a conditional variational principle for general asymptotically
additive potentials by requiring only existence and uniqueness of equilibrium states
for a dense subspace of potential functions.
Keywords:
Multifractal Analysis,
 -Dimension Spectra, Asymptotically
Additive
-Dimension Spectra, Asymptotically
Additive

1. Introduction
The theory of multifractal analysis is a subfield of the dimension theory in dynamical
systems. A general framework for multifractal analysis of dynamical systems was
laid out in [1] [2] . It studies a global dimensional quantity that assigns to each
level set a “size” or “complexity”, such as its topological entropy or Hausdorff
dimension. Broadly speaking, let
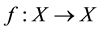 be a continuous transformation of a compact metric space; let
be a continuous transformation of a compact metric space; let ,
,
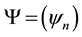 be potential
functions defined on
be potential
functions defined on
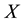 with value in
with value in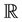 .
Given
.
Given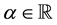 , we consider
the level set:
, we consider
the level set:
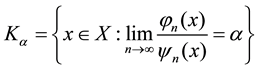
The dimension spectrum
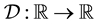 (of potential
(of potential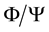 )
is defined by
)
is defined by
 which has been extensively studied for Hólder continuous potentials for
which has been extensively studied for Hólder continuous potentials for
 conformal repellers in [3] - [5] .
conformal repellers in [3] - [5] .
In [6] , Barreira, Saussol, and Schmeling extended their work to higher-dimensional
multifractal spectra, moreover, for which they consider the more general
 -dimension
in place of the topological entropy. Precisely, they consider functions
-dimension
in place of the topological entropy. Precisely, they consider functions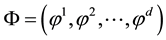 ,
,
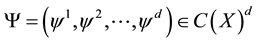 with
with

for




Given a positive function





Theorem 1. Assume that the metric entropy of


If



(I)

(II)

(III) There exists ergodic measure



In [7] , Barreira and Doutor study the spectrum of the





In [8] Climenhaga proved a generalisation of Theorem 1 provided that there is a
dense subspace of

This paper is devoted to the study of higher-dimensional multifractal analysis for
the class of asymptotically additive potentials. We consider the multifractal behavior
of

Section 2 gives definitions and notions, and Section 3 gives precise formulations of the result and proofs.
2. Preliminaries
We recall in this section some notions and results from the thermodynamic formalism.
2.1. Nonadditive Topological Pressure
We first introduce the notion of nonadditive topological pressure. We also refer the reader to [2] and [7] for further references.
Let












Now let



We always assume that

For each


Given a set


where the infimum is taken over all finite or countable collections

It was shown in [9] that the limit
exists. The number







The following proposition was established in [2] .
Proposition 1. For any
2.2.

We recall here a notion introduced by Barreira and Schmeling in [10] . Let

where



Theorem 2. ( [10] ) The following limits exist:
We call







Proposition 2. The number





Furthermore, given a probability measure


We can show that the limit





2.3. Asymptotically Additive Sequences
This kind of potential was introduced by Feng and Huang ( [11] ).
Definition 1. A sequence




We denote by

Proposition 3. If



(I) The limit


(II) The limit

(III) If




(IV) The function


Proposition 4. If



We call


Note that if the function


3. Main Result
Let






We assume that
(1) There exists constant




(2) For every



Given
and function


We also consider the function

Given vectors


and
We also consider the positive sequence of functions


Our main result is the following theorem.
Theorem 3. Let





If



(I)

(II)

(III) There exists ergodic measure



which is arbitrarily close to
Proof. We first establish several auxiliary results.
Lemma 1. For




where

Proof. For any


Therefore, there exists


and thus

Lemma 2. If

Proof. Using (5), a slight modification of the proof of Lemma 2 in [7] yields this statement, and thus we omit it. □
Lemma 3. If



Proof. Take













Now proceed with the proof of (1) in theorem 3. We use analogous arguments to those in the proof of lemma 3 in [7] . First show that
Let




Given



and hence

where

Since
we obtain:
Since
It implies that









Note that







(1)




(2)
(3)
Therefore,
and thus
Denote




For each vector




If
Now assume that



This shows that

satisfying
Similarly, one can consider



For each

is continuous. Moreover,













We claim that there exists an equilibrium measure



Let us assume that such a measure does not exist. We denote by


is a compact convex subset of




For every
which contradicts (7). This completes the proof of claim. Observe that this claim
implies
By lemma 2, for the measure

and hence
We now to prove the reverse inequality. We need the following lemma.
Lemma 4. ([8] ) Under the assumptions of theorem 3, for


In fact, this is a particular case of Theorem C in [8] .
For any



and hence by proposition 2 we have

and thus

Furthermore, since the map


This completes (I) of theorem 3.
We now proceed with the proof of (II) and (III). By lemma 2 we have
for every
On the other hand, for any

and hence
By ergodic decomposition we obtain
For any


Note that
It follows that statement (III) in theorem 3 holds. □
Acknowledgements
The author wishes to thank Professor Cao Yongluo for his invaluable suggestions and encouragement.
References
- Barreira, L., Pesin, Y. and Schmeling, J. (1997) On a General Concept of Multifractality: Multifractal Spectra for Dimensions, Entropies, and Lyapunov Exponents. Multifractal Rigidity. Chaos, 7, 27-38. http://dx.doi.org/10.1063/1.166232
- Pesin, Y. (1997) Dimension Theory in Dynamical Systems: Contemporary Views and Applications. Chicago Lectures in Mathematics, Chicago University Press, Chicago. http://dx.doi.org/10.7208/chicago/9780226662237.001.0001
- Barreira, L. and Saussol, B. (2001) Variational Principles and Mixed Multifractal Spectra. Transactions of the American Mathematical Societyy, 353, 3919-3944. http://dx.doi.org/10.1090/S0002-9947-01-02844-6
- Pesin, Y. and Weiss, H. (1997) A Multifractal Analysis of Equilibrium Measures for Confromal Expanding Maps and Moran-Like Geometric Constructions. Journal of Statistical Physics, 86, 233-275. http://dx.doi.org/10.1007/BF02180206
- Weiss, H. (1999) The Lyapunov Spectrum of Equilibrium Measures for Conformal Expanding Maps and Axiom-A Surface Diffeomorphisms. Journal of Statistical Physics, 95, 615-632. http://dx.doi.org/10.1023/A:1004591209134
- Barreira, L., Saussol, B. and Schmeling, J. (2002) Higher-Dimensional Multifractal Analysis. Journal de Mathémati- ques Pures et Appliquées, 81, 67-91. http://dx.doi.org/10.1016/S0021-7824(01)01228-4
- Barreira, L. and Doutor, P. (2009) Almost Additive Multifractal Analysis. Journal de Mathématiques Pures et Appliquées, 92, 1-17. http://dx.doi.org/10.1016/j.matpur.2009.04.006
- Climenhaga, V. (2013) Topological Pressure of Simultaneous Level. Nonlinearity, 26, 241-268. http://dx.doi.org/10.1088/0951-7715/26/1/241
- Barreira, L. (1996) A Nonadditive Thermodynamic Formalism and Applications to Dimension Theory of Hyperbolic Dynamical Systems. Ergodic Theory and Dynamical Systems, 16, 871-927. http://dx.doi.org/10.1017/S0143385700010117
- Barreira, L. and Schmeling, J. (2000) Sets of “Non-Typical” Points Have Full Topological Entropy and Full Hausdorff Dimension. Israel Journal of Mathematics, 116, 29-70. http://dx.doi.org/10.1007/BF02773211
- Feng, D. and Huang, W. (2010) Lyapunov Spectrum of Asymptotically Sub-Additive Potential. Communications in Mathematical Physics, 297, 1-43.






























































