Received 18 April 2014; revised 20 May 2014; accepted 5 June 2014

ABSTRACT

I utilize a differentiable dynamical system á la Lotka-Voletrra and explain monetary and fiscal interaction in a supranational monetary union. The paper demonstrates an applied mathematical approach that provides useful insights about the interaction mechanisms in theoretical economics in general and a monetary union in particular. I find that a common central bank is necessary but not sufficient to tackle the new interaction problems in a supranational monetary union, such as the free-riding behaviour of fiscal policies. Moreover, I show that supranational institutions, rules or laws are essential to mitigate violations of decentralized fiscal policies.

Keywords:

Differential Equations, Monetary-Fiscal Interaction, Monetary Union Theory

1. Introduction

This paper studies the theoretical implications of monetary and fiscal interaction in a monetary union. This is an urgent and interesting topic, especially since the European sovereign debt crisis in 2010. I utilize an approach from applied mathematics in order to model the economic interactions in a supranational monetary union. A dif- ferentiable dynamical system, similar to a Lotka-Volterra model, turns out to be well suited for studying this pro- blem. Overall, my mathematical model is literally interdisciplinary and links two, up to now, hardly unconnect- ed areas: the theory of differential equations and monetary economics.

It is not surprising that there are relatively few economic models that capture the sophisticated subspace of monetary-fiscal interaction. This has to do with the complexity and dynamics in this field of economics. So far, it is common practice in the economics literature to apply a game theoretic approach to study this question [1] - [4] . However, these models lack of dynamics and fail to incorporate the complexity of monetary-fiscal interac- tion. Consequently, a new applied mathematical model in theoretical economics needs to be both tractable and comprehensible for mathematical economists. I build such a model based on differential equations.

The remainder of the paper is structured as follows: Section 2 explains the model and discusses some propo- sitions. I show the existence, stability and solution of the model as well as the economic implications in general. Finally, Section 3 concludes the paper.

2. The Model

2.1. Economic Model

The model’s framework consists of three interacting institutions. The first institution is the European Central Bank (ECB) that is centralized in a monetary union. The primary objective of monetary policy is to maintain price-stability according to Article 105 in the Treaty on the Functioning of the European Union (TFEU). The ECB, however, interacts with the decentralized fiscal policies, the second institution in the model. Both insti- tutions, in particular the central bank, determine the common interest rate. At the moment, there are 18 member countries and thus fiscal policies in the euro area. The main difference between monetary and fiscal policy is that the fiscal authorities retain full sovereignty at the national level. The third institution is supranational law or governance, such as the Stability and Growth Pact (SGP), the European Stability Mechanism (ESM) and other legal constraints [5] . The supranational rules and laws mainly limit the decentralized fiscal policies and support the goals of the centralized monetary policy. The major problem in a monetary union is known as fiscal policy free-riding and moral hazard [6] - [8] . Consequently, the model consists of three interaction channels:

a) Monetary policy interacts with fiscal policy. The decision about the level of public deficits and debts have an impact on the common central bank.

b) Fiscal policy in one member country interacts with the other fiscal policies in the monetary union. There is competition about the public good “price-stability” provided by ECB. One fiscal policy can undermine the supranational objective and transfer the cost to all countries; i.e. through free-riding.

c) Supranational law defines the level playing field for all institutions. These rules interact with both fiscal policies and the central bank. The main objective is the mitigation of fiscal heterogeneity as well as free-riding and moral hazard.

The paper analyzes these interaction channels in a monetary union in general. I utilize a mathematical model that consists of differential equations. Until now, economic literature has studied these interactions mainly in game theoretic models [2] . The first model in this field of literature was developed by Beetsma and Uhlig [5] . All economic models lack of a rigorous modeling of the full interactions and the simultaneous linkages. More- over, the economic literature focuses on the level of nominal and real variables and it does not study the dy- namic processes [9] . To my knowledge, there is no paper that utilizes a mathematical model based on diffe- rential equations to capture these interactions in a monetary union. Given the current policy challenges in Eu- rope, my model offers important policy lessons.

2.2. Applied Mathematical Model

First of all, I model the interaction of fiscal policies and the supranational law respectively. Suppose, is the number of fiscal policies with excessive national public deficit and debt levels. Hence, 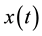measures the number of countries in violation of supranational law, i.e. the Stability and Growth Pact (SGP) which is a simple deficit and debt rule¹. The dynamic yields

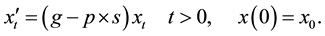(1)

The represents the benefits fiscal policies obtain through debt accumulation and free-riding. Deficit spending induces a short-run growth stimulus and thus higher domestic GDP. But the costs of higher deficits in one country, i.e. higher interest rates, have to be paid by all euro area member countries. The product 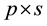re- presents the punishment in case of violation with the supranational debt rule. According to the rule, the punish- ment is a fixed amount, 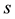, of the GDP (cf. SGP). The parameter, 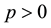, represents the probability of detection of a fiscal policy failure. Hence, the first-order differential Equation (1) has an intuitive economic interpretation. The higher domestic benefits from deficit spending than punishment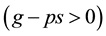, the greater the number of fiscal policies violating the supranational debt rule. However, if countries do not consolidate the public budget according to the supranational rule, they have to pay a sanction if it is detected. Hence, the rule should mitigate the number of violating countries.

The solution of the model is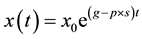. This solution reveals, again, as long as debt accumulation (free-riding incentive) is greater than the sanction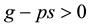, countries prefer free-riding. Only sufficiently high sanctions, , or a high detection probability, , mitigate the problem. Unfortunately, the enforcement of European law is rather weak and thus, 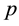, is low in reality [10] [11] . Moreover, the sanction scheme, 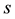, is ra- ther limited today as well². A more comprehensive modeling of the sanction scheme is

(2)

The sanction payment 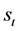depends on a fixed rate and variable rate. The parameter depends on the number of breaching fiscal policies, , and is economically a marginal propensity of sanctions. After subs- titution of Equation (2) in Equation (1), I obtain

(3)

where is a constant. The differential Equation (3) is a so-called logistic-differential equation or Verhulst-Model. I obtain the solution of that differential equation through integration

(4)

Finally, I solve the equation for,

(5)

This solution has the following boundaries for:

(6)

If supranational law is fully effective, i.e. the detection probability and the fixed sanction are high, then the number of breaching countries converge to zero. However, if, i.e., the number of breaching countries convergence to. Obviously, only fully effective supranational law mi- nimizes the number of breaching countries. In other words, the smaller and the larger, the smaller the number of countries violating the rules. The term could be interpreted as a natural intake capacity of breaching countries in a monetary union.

²The sanction is a linear function of GDP with a minimum payment and a maximum of 0.25 percent of GDP according to EU-Regula- tion No. 1467/97.

Next, I study monetary policy. The main instrument of a common central bank is the interest rate level. Importantly, in a monetary union the key interest rate is an average rate that should be appropriate for almost all member countries. But high domestic public deficits and debts indirectly affect (increase) the common interest rate. Thus, there exists a fiscal policy spill-over to monetary policy through the interest rate channel. For sim- plicity, let me first abstract from the spill-over mechanism. I model the interest rate dynamics, again, through a differential equation

(7)

where is the first derivative and economically the rate of change. In addition, measures the target commitment of the central bank, i.e. low inflation. The greater, the higher the interest rates and the lower inflation. If the common central bank fully commits to the primary objective of price stability³. Hence, in this case the parameter is dominating Equation (7). In the following, I define. Finally, represents a fixed punishment of the common central bank for the free-riding incentives of fiscal policies in a monetary union. Obviously, as already explained, a comprehensive model considers the fiscal spill-over me- chanism, too. Thus, depends on the number of breaching fiscal policies, such as

(8)

where represents the central bank reaction to publicly sound fiscal policies. This group of countries lower the common interest rate. And depicts the effect of breaching (unsound) fiscal policies. These countries endanger inflation in the whole monetary union. Thus, the common central bank has to increase the common rate for all member countries. Consequently, the benefits of domestic deficit spending pass through a higher interest rate to all member countries. Furthermore, I generalize. The incentive of free-riding is dependent on the interest rate level:

(9)

where represents the free-rider incentives in a monetary union [4] and measures the disciplining effect of higher interest rates on the free-riding behaviour. In the next section, I study the complete fiscal-mo- netary interaction.

2.3. General Mathematical Model

Analyzing the complete dynamics of the fiscal-monetary-law interaction reveals new insights about the ne- cessary and sufficient conditions for a long-run stable and sustainable monetary union. Using Equations (3) and (7) together with conditions (8) and (9), yields the following system:

(10)

Interestingly, this system of two differential equations is similar to a so-called “Lotka-Volterra” model, de- veloped by Alfred James Lotka (1880-1949) and Vito Volterra (1860-1949), and is an useful concept in appli- ed mathematics [12] . To understand how the fiscal-monetary-law model evolves over the time, I first simplify the equations and assume. This system has two possible solutions and:

The asymptotic stability or instability of the model can be studied. I define the function and cal- culate the eigenvalues. The function is,

(11)

The first derivative for the two solutions yields

Consequently, the eigenvalues of are computed by.

This implies and. From an economic point of view , and thus and. The system is instable, if and. Hence, is an instable equilibrium. The

instability can also be seen from. To determine the eigenvalue for, I

solve the following problem

(12)

The second solution of the model is instable again, due to and

or vice versa. But if, I obtain. Hence, there is the possibility of complex eigenvalues.

This implies no real solution. Finally, I describe the solution behaviour of the model near a point, if the eigenvalues are complex. First, I rewrite the system as

(13)

Next, I integrate and obtain,

(14)

where is an integration constant. Consequently, all solutions satisfy the implicit solution:

(15)

The integration constant can be calculated from the initial condition:

I suggest that satisfy a closed-form

solution in the environment around the point,

(16)

where, and. For and trivial aggregation it results:

(17)

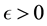
The second-order Taylor approximation of the solution in the environment of and yields, which is equivalent to:

(18)

This shows that that the specific solution solves the model for until an error term of order. Moreover, the ‘trajectories’ are approximative ellipses around the point. The model reveals an interesting economic interpretation for: the model has an equilibrium with a certain number of fiscal policies breaching the supranational deficit and debt rule as long as the supranational law and central bank are ineffective and do not intervene in case of fiscal policy violations.

Finally, I study the full model of Equation (10) with. Again, I calculate the solutions and prove the stability of the associated equilibria. I obtain

(19)

The general model has four solutions:

and is the solution of the following linear system

Applying Cramer’s rule, I obtain

For later computation purposes, I define and. The stability of the solutions are computed via the function. The derivative yields

(20)

The point is non-stationary because. The second solution is non- stationary because. The point is unstable, if or asymptotically stable,

if. The point has positive values, i.e., for. The

eigenvalues of Equation (20) for are:

where and they are defined as above. As long as, the point is asymptotically stable. That means for. Economically, it implies a certain number of fiscal policies violating the supranational deficit and debt rule. The following expressions summarize the results, for:

(21)

The first constellation becomes a reality if free-rider incentives are small and the number of dis- ciplined fiscal policies are great. The next proposition reveals an answer to the following question: Is a supranational central bank sufficient to constrain the number of fiscal policies violating the supranational debt rule in a monetary union?

Proposition 1 The number of fiscal policies in violation with a debt rule is always positive in a mo- netary union, as long as, , and are non-zero.

The proof of this proposition follows from Equation (21). First, the constellation is eco-

nomically not realistic because the common interest rate converges for to infinity, to zero. Any- way, even in this case the number of breaching fiscal policies converge to a positive fixed ratio. For the second constellation and is always positive, too. This is surprising because it demonstrates that the common cental bank is ineffective in mitigating the free-riding incentives through higher interest rates. Consequently, effective supranational governance, that prevents debt accumulation of fiscal policies, is essential in a monetary union. Proposition 1 reveals that supranational governance is only effective if both the detection probability and the marginal sanction fee is high. In this case and declines because the free-riding incentives are less attractive. Unfortunately, the existing European fiscal and economic governance scheme is neither effective nor rigorously enforced. Consequently, the current sanction procedure in the Euro- pean Monetary Union (EMU) has a low detection probability and a weak enforcement. Moreover, there are too many exceptions as well as loopholes, and the whole governance is under flawed partisan influence. Overall, this explains the importance of sustainable public finances and an efficient fiscal and economic governance scheme in a monetary union. Otherwise, a monetary union is doomed to fail. The final proposition discusses the sensitivity of the general model.

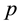
Proposition 2 For, the number of fiscal policies violating supranational law and the common interest rate, except for (iii), is low, if

a) the detection probability, , is high;

b) the marginal sanction fee, , is high;

c) central bank commitment, d, is high (i.e. c is low).

Proof: The proof follows by direct differentiation of and:

Part (ii), follows by differentiation in respect to,

Part (iii) is shown by

3. Conclusion

This paper explains the unique fiscal-monetary-law interaction in a supranational monetary union. I conclude the paper by discussing some generalizations and by touching on some issues that the model did not address. First, the argument is much more general than initially considered. The results reveal new insights about the interac- tion of the key institutions in a monetary union. The model demonstrates that without effective laws and fiscal and economic governance, a monetary union is doomed to fail. Consequently, the fiscal and economic govern- ance scheme, together with the common cental bank, plays an important role in a monetary union. Second, the model is well designed to analyze the institutional drawbacks and interaction relationships in the EMU. The re- sult suggests a tough sanction scheme for unsound fiscal policies. Only this can mitigate the potential benefits of free-riding. The major omission of the model is an endogenous economic-political element that considers for in- stance strategic policy decisions or veto power. Furthermore, an empirical investigation of the proposition is also an important study object in future research. Moreover, I do not consider the fact that small and weak agents ty- pically pay more attention to supranational law than powerful agents do.

Acknowledgements

I would like to thank for comments Mr. Gassmann and the two anonymous referees. I gratefully acknowledge financial support from the RRI-Reutlingen Research Institute.

References

NOTES

¹The Stability and Growth (SGP) limits public deficits to 3% of GDP and debt to 60% of GDP.

³According to article 105 TFEU “... the primary objective of the... [European Central Bank]... is price stability.” The US-Federal Reserve Bank, however, has a dual mandate which means a lower d.