Journal of Applied Mathematics and Physics
Vol.02 No.04(2014), Article ID:43435,9 pages
10.4236/jamp.2014.24001
Couette Flow Problem for an Unsteady MHD Fourth-Grade Fluid with Hall Currents
Haider Zaman*, Tarique Abbas, Arif Sohail, Azhar Ali
Faculty of Numerical Sciences, Islamia College University, Peshawar, Pakistan
Email: *haiderzaman67@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 January 2014; revised 12 February 2014; accepted 20 February 2014
ABSTRACT
In this work, we analyze Couette flow problem for an unsteady magnetohydrodynamic (MHD) fourth-grade fluid in presence of pressure gradient and Hall currents. The existing literature on the topic shows that the effect of Hall current on Couette flow of an unsteady MHD fourth-grade fluid with pressure gradient has not been investigated so far. The arising non-linear problem is solved by the homotopy analysis method (HAM) and the convergence of the obtained complex series solution is carefully analyzed. The influence of pressure number, Hartmann number, Hall parameter and fourth-grade material parameters on the unsteady velocity is discussed through plots and on local skin-friction coefficient discussed through numerical values presented in tabular form.
Keywords:
Couette Flow; Hall Currents; Unsteady; Fourth-Grade Fluid; HAM

1. Introduction
In fluid mechanics, everyone is familiar with Couette flow problem, the flow between two parallel plates in which bottom plate is fixed and upper plate is initially at rest and is suddenly set into motion in its own plane with a constant velocity, is termed as Couette flow [1] [2] . Bhaskara and Bathaiah [3] have analyzed Couette flow problem with Hall effects for flow through a porous straight channel. Ganapathy [4] wrote a note on the oscillatory Couette flow in a rotating system. Erdogan [5] solved unsteady Couette flow for viscous fluid by Laplace transform method. Stokes and Couette flows due to an oscillating wall are discussed by Khaled and Vafai [6] . Hayat et al. [7] used Laplace transform method to determine the analytic solutions of Couette flows of a second grade fluid. Oscillatory Couette flow is studied by Singh [8] . Guria [9] discussed Couette flow problem for rotating and oscillatory flow. Couette flow of an unsteady third-grade fluid with variable magnetic field is
investigated by Hayat and Kara [10] , here fluid is in an annular region between two coaxial cylinders. The axial Couette flow problem of an electrically conducting fluid in an annulus is examined by Hayat et al. [11] . Das et al. [12] studied unsteady Couette flow problem in a rotating system. Recently, Zaman et al. [13] presented solution for unsteady Couette flow problem for the Eyring-Powell model. When a strong magnetic field is applied in an ionized gas of low density, the conductivity normal to the magnetic field is decreased by free spiraling of electrons and ions about the magnetic lines of force before suffering collisions. This phenomenon is known as Hall effect and a current induced in a direction normal to the electric and magnetic fields is called Hall current [15] . The study of the Effects of Hall current on flow of non-Newtonian fluids [15] -[23] is important because of its applications in power generators and pumps, Hall accelerators, refrigeration coils, electric transformers, in flight MHD, electronic system cooling, cool combustors, fiber and granular insulation, oil extraction, thermal energy storage and flow through filtering devices.
In order to understand the interaction of electric, magnetic, and hydrodynamic forces in the unsteady fourth-grade fluid, we considered a simple flow problem, known as the Couette flow. The effects of pressure gradient and Hall current on the flow are also taken into account. The complex analytic solution for non-linear problem is found by using the homotopy analysis method (HAM) [24] -[31] . This solution is valid for all values of the time in the whole spatial domain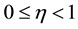 . The convergence of the analytic solution is ensured with the help of
. The convergence of the analytic solution is ensured with the help of . The effects of pressure number, Hartmann number, Hall parameter, second-grade parameter, third-grade and fourth grade parameters on the unsteady velocity are illustrated through plots. Also the effects of the pertinent parameters on the local skin friction coefficient at the surface of the wall are presented numerically in tabular form.
. The effects of pressure number, Hartmann number, Hall parameter, second-grade parameter, third-grade and fourth grade parameters on the unsteady velocity are illustrated through plots. Also the effects of the pertinent parameters on the local skin friction coefficient at the surface of the wall are presented numerically in tabular form.
2. Formulation of the Problem and Its Analytic Solution
Consider the unsteady flow of an electrically conducting incompressible fourth-grade fluid between two parallel flat plates, subjected to a uniform transverse magnetic field. We assume that the bottom plate is fixed and the top plate is stationary when 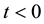 and at
and at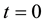 , the top plate starts moving impulsively in its own plane with a constant velocity
, the top plate starts moving impulsively in its own plane with a constant velocity 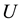 and a pressure gradient is also applied. The flow here is maintained by the motion of the top plate. The Cauchy stress tensor
and a pressure gradient is also applied. The flow here is maintained by the motion of the top plate. The Cauchy stress tensor 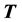 for a fourth-grade fluid is given as [32]
for a fourth-grade fluid is given as [32]
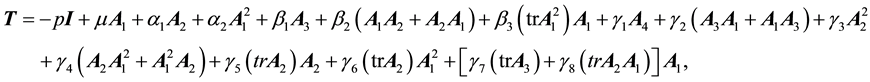 (1)
(1)
where 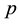 is the scalar pressure,
is the scalar pressure, 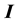 is the identity tensor,
is the identity tensor, 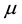 is the coefficient of viscosity,
is the coefficient of viscosity, 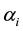 ,
, 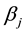 ,
, 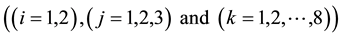
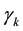 are the material parameters of fourth-grade fluid, and
are the material parameters of fourth-grade fluid, and 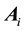
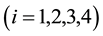 are the first four Rivlin-Ericksen tensors defined by [32]
are the first four Rivlin-Ericksen tensors defined by [32]

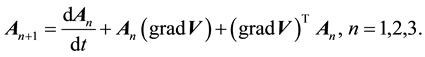
The equations governing the magnetohydrodynamic flow with Hall effect are:


The boundary and initial conditions are

where 






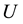
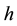
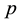
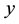

where 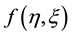



where prime denotes differentiation with respect to







modified Hartmann number [33] . The local skin friction coefficient or fractional drag coefficient on the surface of the moving wall is

Now using Equations (1)-(3) and (7) the Equation (10) can be written in dimensionless variables as
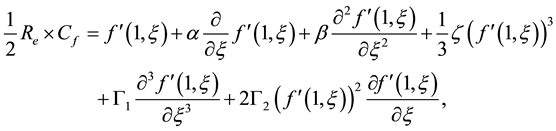
where 
The boundary conditions (9) lead us to take base functions for the velocity 
The velocity 

To start with the homotopy analysis method, due to the boundary conditions (9) it is reasonable to choose the initial guess approximation

and the auxiliary linear operator
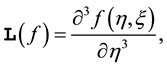
with the property:

where



At







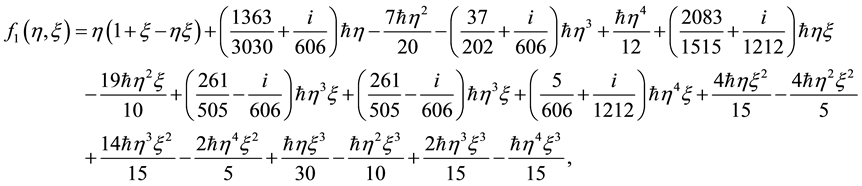
similarly



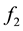

The total complex analytic solution in compact form is

where from initial guess in Equation (14) we obtain

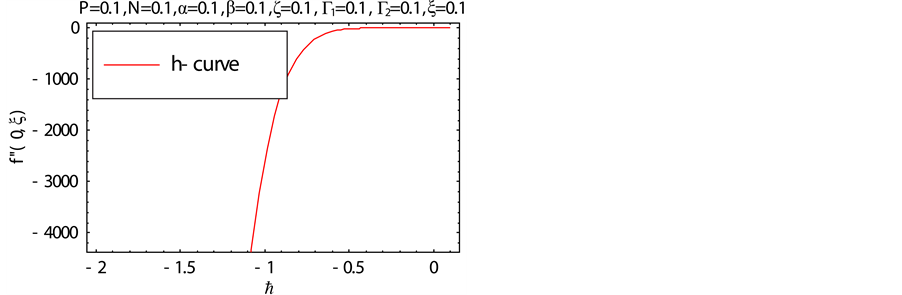
all other unknown constants can be determined by utilizing first nine given in Equation (21) by using the recurrence relations, which we calculated but it is not possible to write here due to their length. We know that the auxiliary parameter 


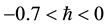


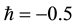
3. Graphs, Tables and Discussion
The discussion of emerging parameters on the dimensionless velocity 
Figures 2 to 10 are plotted in absence of Hall currents and in Figure 11 Hall current is taken into account. Figure 2 displays the velocity 

Figure 1. 
Figure 2. Influence of η on f(η, ξ).
Figure 3. Influence of ξ on f(η, ξ).
Figure 4. Influence of N on f(η, ξ).
bottom plate to towards the moving top plate the velocity increases for all values of the time, even the fluid close to the upper plate moves with the same velocity as of the upper plate and the fluid close to the bottom plate has nearly zero velocity. Figure 3 presents the velocity profile 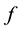
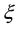
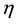


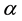
Figure 5. Influence of α on f(η, ξ).
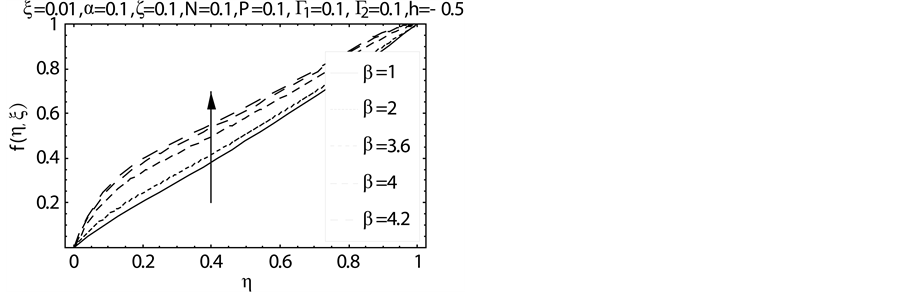
Figure 6. Influence of β on f(η, ξ).
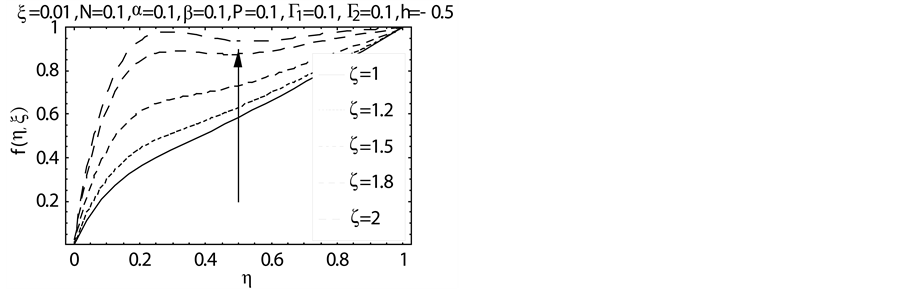
Figure 7. Influence of ζ on f(η, ξ).
distribution is presented for the various values of third-grade parameters 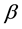

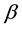
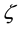
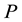
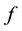





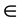
It is observed from Table 1 that with increase in Hartmann number 
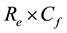
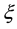


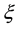
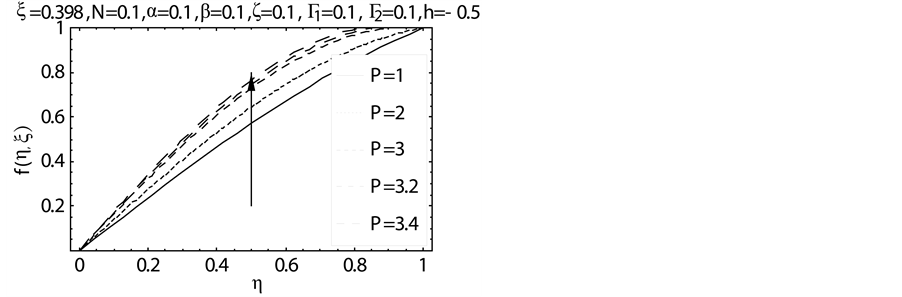
Figure 8. Influence of P on f(η, ξ).
Figure 9. Influence of Γ1 on f(η, ξ).
Figure 10. Influence of Γ2 on f(η, ξ).
in the absolute value of the skin friction coefficient. Increase in pressure number
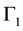

4. Conclusion
The Couette flow between two parallel plates filled with MHD unsteady fourth-grade fluid is studied analytically. The effects of the pressure and Hall current are also incorporated. A non-linear fourth-grade model for the fluid is used. The model is invoked into the governing equations and the resulting one dimensional equation for unsteady MHD flow is derived. This equation is solved by HAM in general to study the sensitivity of the flow to
Figure 11. Influence of 
Table 1. Absolute values of the skin friction coefficient Re × Cf with α = 0.1, β = 0.1, ζ = 0.1, Γ1 = 0.1, Γ2 = 0.1,
Table 2. Absolute values of the skin friction coefficient Re × Cf with α = 0.1, β = 0.1, ζ = 0.1, ξ = 0.1, P = 0.1,
the parameters that are used in the fourth-grade model. The various dimensionless parameters seem to affect the velocity a lot. The velocity profile and local skin friction coefficient are greatly influenced by the Hall parameter, fourth-grade fluid parameters, pressure and Hartmann numbers.
References
- Schlichting, H. (1968) Boundary Layer Theory. 6th Edition, McGraw-Hill, New York.
- White, F.M. (1991) Viscous Fluid Flow. McGraw-Hill, New York.
- Bhaskara, R. and Bathaiah, N.D. (1982) Halll Effects on MHD Couette Flow through a Porous Straight Channel. Defense Science Journal, 32, 313-326.
- Ganapathy, R. (1994) A Note on Oscillatory Couette Flow in a Rotating System. Journal of Applied Mechanics, 61, 208. http://dx.doi.org/10.1115/1.2901403
- Erdogan, M.E. (2002) On the Unsteady Unidirectional Flows Generated by Impulsive Motion of a Boundary or Sudden Application of a Pressure Gradient. International Journal of Non-Linear Mechanics, 37, 1091-1106. http://dx.doi.org/10.1016/S0020-7462(01)00035-X
- Khaled, A.R.A. and Vafai, K. (2004) The Effect of the Slip Condition on Stokes and Couette Flows Due to an Oscillating Wall: Exact Solutions. International Journal of Non-Linear Mechanics, 39, 795-809. http://dx.doi.org/10.1016/S0020-7462(03)00043-X
- Hayat, T., Khan, M., Ayub, M. and Siddiqui, A.M. (2005) The Unsteady Couette Flow of a Second Grade Fluid in a Layer of Porous Medium. Archives of Mechanics, 57, 405-416.
- Singh, K.D., Gorla, M.G. and Raj, H. (2005) A Periodic Solution of Oscillatory Couette Flow through Porous Medium in Rotating System. Indian Journal of Pure and Applied Mathematics, 36, 151-159.
- Guria, M., Jana, R.N. and Ghosh, S.K. (2006) Unsteady Couette Flow in a Rotating System. International Journal of Non-Linear Mechanics, 41, 838-843. http://dx.doi.org/10.1016/j.ijnonlinmec.2006.04.010
- Hayat, T. and Kara, A.H. (2006) Couette Flow of a Third-Grade Fluid with Variable Magnetic Field. Mathematical and Computer Modelling, 43, 132-137. http://dx.doi.org/10.1016/j.mcm.2004.12.009
- Hayat, T., Momoniat, E. and Mahomed, F.M. (2008) Axial Couette Flow of an Electrically Conducting Fluid in an Annulus. International Journal of Modern Physics B, 22, 2489-2500. http://dx.doi.org/10.1142/S0217979208039587
- Das, S., Maji, S.L., Guria, M. and Jana, R.N. (2009) Unsteady MHD Couette Flow in a Rotating System. Mathematical and Computer Modelling, 50, 1211-1217. http://dx.doi.org/10.1016/j.mcm.2009.05.036
- Zaman, H., Shah, M.A. and Ibrahim, M. (2013) Unsteady Incompressible Couette Flow Problem for the Eyring-Powell Model with Porous Walls. American Journal of Computational Mathematics, 3, 313-325. http://dx.doi.org/10.4236/ajcm.2013.34041
- Sato, H. (1961) The Hall Effects in the Viscous Flow of Ionized Gas between Parallel Plates under Transverse Magnetic Field. Journal of the Physical Society of Japan, 16, 1427-1433. http://dx.doi.org/10.1143/JPSJ.16.1427
- Katagiri, M. (1969) The Effect of Hall Currents on the Magnetohydrodynamic Boundary Layer Flow Past a Semi-Infinite Flate Plate. Journal of the Physical Society of Japan, 27, 1051-1059. http://dx.doi.org/10.1143/JPSJ.27.1051
- Pop, I. and Soundalgekar, V.M. (1974) Effects of Hall Current on Hydromagnetic Flow near a Porous Plate. Acta Mechanica, 20, 315-318. http://dx.doi.org/10.1007/BF01175933
- Gupta, A.S. (1975) Hydromagnetic Flow past a Porous Flate Plate with Hall Effects. Acta Mechanica, 22, 281-287. http://dx.doi.org/10.1007/BF01170681
- Debnath, L., Ray, S.C. and Chatterjee, A.K. (1979) Effects of Hall Current on Unsteady Hydromagnetic Flow past a Porous Plate in a Rotating Fluid System. Zeitschrift für Angewandte Mathematik und Mechanik, 59, 469-471. http://dx.doi.org/10.1002/zamm.19790590910
- Khan, M., Asghar, S. and Hayat, T. (2009) Hall Effect on the Pipe Flow of a Burgers’ Fluid: An Exact Solution. Nonlinear Analysis: Real World Applications, 10, 974-979. http://dx.doi.org/10.1016/j.nonrwa.2007.11.016
- Hayat, T., Zaman, H. and Ayub, M. (2010) Analytic Solution of Hydromagnetic Flow with Hall Effect over a Surface Stretching with a Power Law Velocity. Numerical Methods for Partial Differential Equations, 27, 937-959. http://dx.doi.org/10.1002/num.20562
- Ahmad, M., Zaman, H. and Rehman, N. (2010) Effects of Hall Current on Unsteady MHD Flows of a Second Grade Fluid. Central European Journal of Physics, 8, 422-431. http://dx.doi.org/10.2478/s11534-009-0083-z
- Ayub, M., Zaman, H. and Ahmad, M. (2010) Series Solution of Hydromagnetic Flow and Heat Transfer with Hall Effect in a Second Grade Fluid over a Stretching Sheet. Central European Journal of Physics, 8, 135-149. http://dx.doi.org/10.2478/s11534-009-0110-0
- Zaman, H. (2013) Hall Effects on the Unsteady Incompressible MHD Fluid Flow with Slip Conditions and Porous Walls. Applied Mathematics and Physics, 1, 31-38.
- Liao, S.J. (2003) Beyond Perturbation: Introduction to Homotopy Analysis Method. Chapman and Hall, CRC Press. http://dx.doi.org/10.1201/9780203491164
- Liao, S.J. (1992) The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problem. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai.
- Liao, S.J. (2012) Homotopy Analysis Method in Nonlinear Differential Equations. Higher Education Press, Beijing. http://dx.doi.org/10.1007/978-3-642-25132-0
- Liao, S.J. (2013) Advances in the Homotopy Analysis Method. World Scientific Publishing Company.
- Liao, S.J. (2009) Notes on the Homotopy Analysis Method: Some Definitions and Theorems. Communications in Nonlinear Science and Numerical Simulation, 14, 983-997. http://dx.doi.org/10.1016/j.cnsns.2008.04.013
- Ayub, M., Zaman, H., Sajid, M. and Hayat, T. (2008) Analytical Solution of Stagnation-Point Flow of a Viscoelastic Fluid towards a Stretching Surface. Communications in Nonlinear Science and Numerical Simulation, 13, 1822-1835. http://dx.doi.org/10.1016/j.cnsns.2007.04.021
- Zaman, H. and Ayub, M. (2010) Series Solution of Unsteady Free Convection Flow with Mass Transfer along an Accelerated Vertical Porous Plate with Suction. Central European Journal of Physics, 8, 931-939. http://dx.doi.org/10.2478/s11534-010-0007-y
- Zaman, H., Hayat, T., Ayub, M. and Gorla, R.S.R. (2011) Series Solution for Heat Transfer from a Continuous Surface in a Parallel Free Stream of Viscoelastic Fluid. Numerical Methods for Partial Differential Equations, 27, 1511-1524. http://dx.doi.org/10.1002/num.20593
- Rivlin, R.S. and Ericksen, J.L. (1955) Stress Deformation Relations for Isotropic Materials. Journal of Rational Mechanics and Analysis, 4, 323-425.
- Sutton, G.W. and Sherman, A. (1965) Engineering Magnetohydrodynamics. McGraw-Hill, New York.
NOTES
*Corresponding author.