Journal of Applied Mathematics and Physics
Vol.2 No.2(2014), Article ID:42094,9 pages DOI:10.4236/jamp.2014.22001
Schrödinger Operators on Graphs and Branched Manifolds
Department of Differential Equations and Mathematical Physics, Peoples’ Friendship University of Russia, Moscow, Russia
Email: mohnuman@hotmail.com
Received December 3, 2013; revised January 3, 2014; accepted January 9, 2014
ABSTRACT
We consider the Schrödinger operators on graphs with a finite or countable number of edges and Schrödinger operators on branched manifolds of variable dimension. In particular, a description of self-adjoint extensions of symmetric Schrödinger operator, initially defined on a smooth function, whose support does not contain the branch points of the graph and branch points of the manifold. These results are obtained for graphs with a single vertex, graphs with multiple vertices and graphs with a single vertex and countable set of rays.
Keywords:The Schrödinger Equation; Schrödinger Operators on Graphs and Branched Manifolds; Self-Adjoint Extensions
1. Introduction
Differential operators on graphs and other branched manifolds have applications to the description of a number of processes in quantum mechanics and biology. Fundamentals of the theory of differential equations on graphs presented in the monograph [1], in which a number of examples of physical problems leading to the study of differential operators on graphs. In the articles [2-4] spectral properties of such operators are investigated by the dynamic properties of the evolution determined by the Schrödinger equation on the graph. In the articles [5-8] we study the set of self-adjoint extensions Schrödinger operator defined initially in the space of compactly supported smooth functions, whose support do not contain the branch points of the graph ([6-8]) or points of changing the operator type [5]. Feynman approximation formulas for the unitary semigroups defined by some of the self-adjoint extensions are founded in the article [7]. This article contains the consideration of the Laplace operators on graphs with a finite or countable number of edges. This article is a continuation of studies [7] in which we studied the graph with a finite set of edges are considered.
The relevant problem under consideration consists of recently considerable interest in the description of particle dynamics on graphs, branched dendrites and other manifolds from mathematical physics and quantum mechanics. Mathematically, the operation of differentiation function is uniquely defined for functions on region or on a smooth manifold, which needs to be clarified for the functions defined on manifolds, containing the branch point. The purpose of this study is to determine the action of the Schrödinger operator on functions defined on a manifold with a finite set of branch points. For this purpose, we define the Schrödinger operator 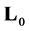 in the space
in the space 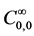 finite and infinitely differentiable functions whose support does not contain the branching points. Schrödinger operator 𝐋 on a graph is called a self-adjoint extension of the operator
finite and infinitely differentiable functions whose support does not contain the branching points. Schrödinger operator 𝐋 on a graph is called a self-adjoint extension of the operator . In this article we describe the set of all operators of Schrödinger operators on a graph in terms of conditions on the set of limit values at the branch point functions in the domain of 𝐋 and its derivative. In this article we obtained the results with a single vertex (they represent a union n of semidirect with a common vertex), graphs with multiple vertices and graphs with a single vertex and a countable set of rays and the set of all operators of Schrödinger on branched manifold in terms of conditions on the set of limit values on a manifold of branching functions in the domain of the operator 𝐋.
. In this article we describe the set of all operators of Schrödinger operators on a graph in terms of conditions on the set of limit values at the branch point functions in the domain of 𝐋 and its derivative. In this article we obtained the results with a single vertex (they represent a union n of semidirect with a common vertex), graphs with multiple vertices and graphs with a single vertex and a countable set of rays and the set of all operators of Schrödinger on branched manifold in terms of conditions on the set of limit values on a manifold of branching functions in the domain of the operator 𝐋.
In this article we found general description of a set of self-adjoint extensions, of the operator , as on graphs and branched manifolds.
, as on graphs and branched manifolds.
2. Formulation of Problem and Notation
We study the Schrödinger operator on the graph Γ, defining the processes of diffusion and quantum dynamics on a graph both on branched manifold. Following [1] terminology graph Γ is called finite or countable collection of smooth one-dimensional manifolds 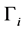 (called edges of the graph), each of which is diffeomorphic to the ray
(called edges of the graph), each of which is diffeomorphic to the ray 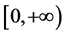 or interval [0,1]. The boundary points of the edges will be called vertices of the graph. Each vertex of a graph is a boundary point of a non-empty set of edges of a graph.
or interval [0,1]. The boundary points of the edges will be called vertices of the graph. Each vertex of a graph is a boundary point of a non-empty set of edges of a graph.
Assumed that on Γ given Borel measure, we determine the requirement that its restriction to each edge 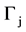 coincides with the standard Lebesgue measure, then
coincides with the standard Lebesgue measure, then .
.
Let 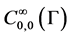 -vector space of infinitely differentiable complex-valued functions on Γ with compact support not containing the vertices, and operator
-vector space of infinitely differentiable complex-valued functions on Γ with compact support not containing the vertices, and operator 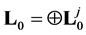 is linear operator defined on a linear space
is linear operator defined on a linear space 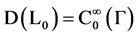 by the equation
by the equation
 (2.1)
(2.1)
in which the functions![]() ,
, ![]() ,
, ![]() -real-valued, bounded and continuous everywhere except at the vertex function on Γ, function
-real-valued, bounded and continuous everywhere except at the vertex function on Γ, function ![]() takes on each edge
takes on each edge 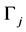 a constant value
a constant value 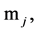 and
and 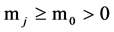 for all
for all 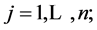
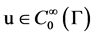 .
.
We say that Γ is branched manifolds, if Γ defined as the union of ![]() instances of regions
instances of regions 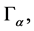
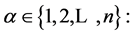
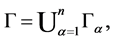 we assume that for each 𝛼 region
we assume that for each 𝛼 region 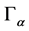 is
is 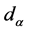 -dimensional bounded domain in the space
-dimensional bounded domain in the space 
with 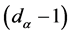 dimensional smooth boundary
dimensional smooth boundary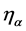 . The boundary of the manifold Γ is defined as the union of
. The boundary of the manifold Γ is defined as the union of ![]() instances of boundaries regions
instances of boundaries regions 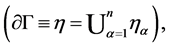 where
where 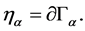
Point 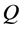 is called a branch point of the manifold Γ, if it is a boundary point of at least two different regions
is called a branch point of the manifold Γ, if it is a boundary point of at least two different regions  where
where 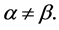
Assumed that on Γ given Borel measure, we determine the requirement that its restriction to each regions 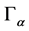 coincides with the standard Lebesgue measure space
coincides with the standard Lebesgue measure space 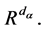 Then the space of square-integrable in the Lebesgue measure on the set of complex-valued functions Γ admits the representation
Then the space of square-integrable in the Lebesgue measure on the set of complex-valued functions Γ admits the representation 
Let  -vector space of infinitely differentiable complex-valued functions on Γ with compact support not containing branch points of the manifold, and
-vector space of infinitely differentiable complex-valued functions on Γ with compact support not containing branch points of the manifold, and  -linear operator defined on
-linear operator defined on  by relation
by relation 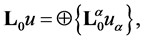 where
where
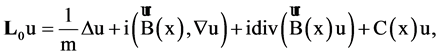 (2.2)
(2.2)
in which the functions![]() ,
, ![]() ,
, ![]() -real-valued, bounded and continuous everywhere except at the branching points of Γ, function
-real-valued, bounded and continuous everywhere except at the branching points of Γ, function ![]() takes on each region
takes on each region 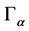 a constant value
a constant value 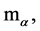 and
and 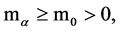 for all
for all 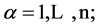
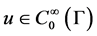 . Here
. Here 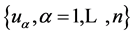 -restricting a function
-restricting a function ![]() on the region
on the region 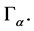
Definition: The linear self-adjoint operator 𝐋 in the space 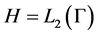 is called Hamiltonian of quantum system with mass
is called Hamiltonian of quantum system with mass ![]() in the electromagnetic filed
in the electromagnetic filed 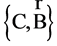 if 𝐋 is self-adjoint extension of the operator
if 𝐋 is self-adjoint extension of the operator 
We investigate the properties of the Cauchy problem for the Schrödinger equation
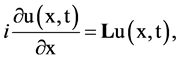 (2.3)
(2.3)
with the initial condition
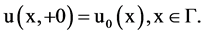 (2.4)
(2.4)
Here 𝐋-symmetric operator in a Hilbert space 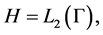 is an extension operator of
is an extension operator of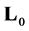 , given on linear manifold
, given on linear manifold  by the equation (2.1) or (2.2). The purpose of the article is to describe the set of all self-adjoint extensions of the operator
by the equation (2.1) or (2.2). The purpose of the article is to describe the set of all self-adjoint extensions of the operator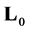 , that may act as generators of the unitary group of the Cauchy problem (2.3), (2.4) for the Schrödinger equation.
, that may act as generators of the unitary group of the Cauchy problem (2.3), (2.4) for the Schrödinger equation.
3. Graph with One Vertex
Graph Γ with one vertex, is defined as the union of ![]() instances of semidirect
instances of semidirect 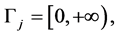
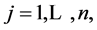 with a common origin
with a common origin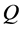 , called the vertex of the graph. Assumed that on Γ given Borel measure defined by the requirement that its restriction to each semidirect
, called the vertex of the graph. Assumed that on Γ given Borel measure defined by the requirement that its restriction to each semidirect  coincides with the standard Lebesgue measure, then
coincides with the standard Lebesgue measure, then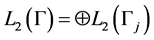 . Let
. Let 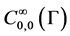 -vector space of infinitely differentiable complex-valued functions on Γ with compact support not containing the point
-vector space of infinitely differentiable complex-valued functions on Γ with compact support not containing the point 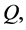 and
and 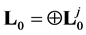 -linear operator, defined on
-linear operator, defined on 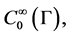 by the relation
by the relation 
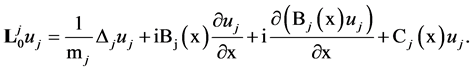
Here 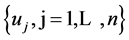 -restriction of a function
-restriction of a function ![]() on semidirect
on semidirect .
.
Assumed that for all ![]() number
number 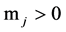 and the function
and the function 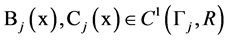 and
and 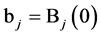 we denote in the point
we denote in the point 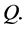
Operator 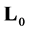 with domain of definition
with domain of definition 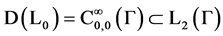 is densely defined and symmetric. The domain
is densely defined and symmetric. The domain 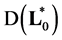 adjoint operator
adjoint operator  is a linear subspace
is a linear subspace  The restriction of any function
The restriction of any function 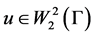 on semidirect
on semidirect 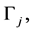
 possess boundary values at the vertex, which we denote by
possess boundary values at the vertex, which we denote by 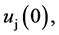 where the symbol
where the symbol 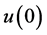 means
means  This is also true for the first derivatives of these restrictions, which use similar notation.
This is also true for the first derivatives of these restrictions, which use similar notation.
Von Neumann theorem ([9,10]) provides a description of a set of self-adjoint extensions of symmetric operators. We obtain an explicit description of a set of self-adjoint extensions of the operator 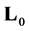 in terms of conditions on a linear subspace in the space of boundary values
in terms of conditions on a linear subspace in the space of boundary values
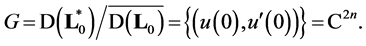
Theorem 1. Let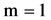 ,
,  and
and 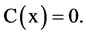 The operator 𝐋 with domain
The operator 𝐋 with domain
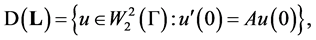
self-adjoint if and only if the matrix 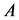 satisfies the equality
satisfies the equality 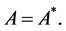
Proof. If 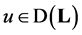 and
and 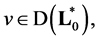 then we have the equality
then we have the equality
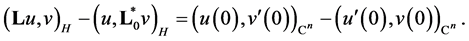
Hence 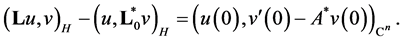
Traces  take arbitrary values, therefore the equality
take arbitrary values, therefore the equality  is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 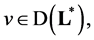 which proves Theorem 1.
which proves Theorem 1.
Corollary 1. If 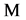 and
and 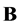 -diagonal matrices and the matrix elements are defined by the formula
-diagonal matrices and the matrix elements are defined by the formula

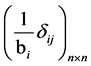
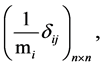 respectively, and
respectively, and 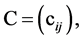 where
where 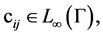 then the operator 𝐋
then the operator 𝐋
with domain 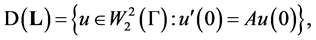 self-adjoint if and only if the matrices
self-adjoint if and only if the matrices 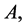
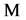 and
and 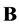 satisfy the equality
satisfy the equality 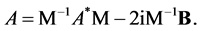
Proof. If 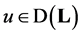 and
and  then we have the equality
then we have the equality
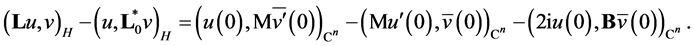
Hence
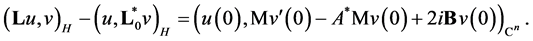
Traces 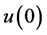 take arbitrary values, therefore the equality
take arbitrary values, therefore the equality  is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 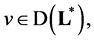 which proves the corollary 1.
which proves the corollary 1.
Theorem 1 gives a description of a wide class of self-adjoint extensions of the operator 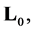 but does not describe the totality of self-adjoint extensions. This makes the next theorem.
but does not describe the totality of self-adjoint extensions. This makes the next theorem.
Theorem 2. The operator 𝐋 is self-adjoint if and only if its domain of definition  consists of the functions in the space
consists of the functions in the space 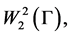 boundary values satisfy the equality
boundary values satisfy the equality 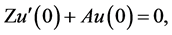 where rank of the matrix
where rank of the matrix 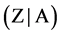 equals
equals ![]() and the matrix is
and the matrix is 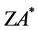 is self-adjoint:
is self-adjoint: 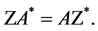
Proof. Let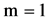 ,
,  and
and 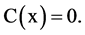 We denote by
We denote by 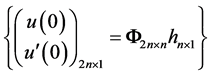 set of solutions of linear equations
set of solutions of linear equations
 (3.1)
(3.1)
where 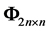 is the fundamental matrix and
is the fundamental matrix and  is a matrix of independent constants. Substituting each of the solutions of the fundamental equation
is a matrix of independent constants. Substituting each of the solutions of the fundamental equation 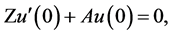 specifying the domain, we obtain by following the relation of the fundamental matrix, with the matrix of the system of equation (3.1)
specifying the domain, we obtain by following the relation of the fundamental matrix, with the matrix of the system of equation (3.1)
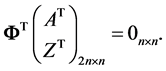 (3.2)
(3.2)
If 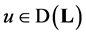 and domain of the operator 𝐋 defined by a system of equation (3.1), then for any
and domain of the operator 𝐋 defined by a system of equation (3.1), then for any 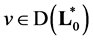 rightly the equality
rightly the equality
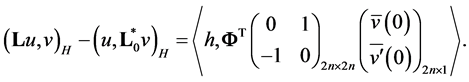
Element 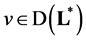 satisfies condition
satisfies condition
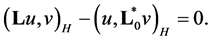 (3.3)
(3.3)
Let 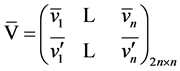 -basis in the linear
-basis in the linear  then each column of matrix
then each column of matrix 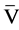 satisfies
satisfies
(3.3), and therefore
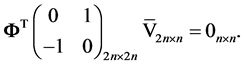 (3.4)
(3.4)
Of (3.2) and (3.4), it follows that the matrix 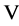 can be selected
can be selected 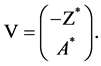
The operator 𝐋 is self-adjoint if and only if 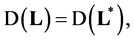 so if
so if 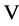 -matrix of the columns of the basis vectors in the subspace
-matrix of the columns of the basis vectors in the subspace  then
then 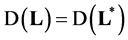 if and only if
if and only if  is also the matrix of the columns of the basis vectors in the subspace
is also the matrix of the columns of the basis vectors in the subspace 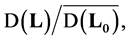 that is, any of its column satisfies the system of equaation (3.1). And this is equivalent to the system of equations
that is, any of its column satisfies the system of equaation (3.1). And this is equivalent to the system of equations 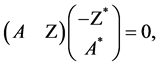 which proves Theorem 2.
which proves Theorem 2.
Theorem 3. The operator 𝐋 is self-adjoint if and only if its domain of definition 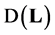 consists of the functions in the space
consists of the functions in the space 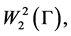 boundary values satisfy the equality
boundary values satisfy the equality 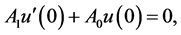 where rank of the matrix
where rank of the matrix  equals
equals ![]() and the matrix is
and the matrix is  is self-adjoint:
is self-adjoint: 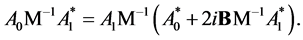
Proof. Let ,
, 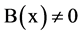 and
and 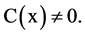 We denote by
We denote by  set of solutions of linear equations
set of solutions of linear equations
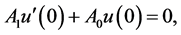 (3.5)
(3.5)
where  is the fundamental matrix and
is the fundamental matrix and  is a matrix of independent constants. Substituting each of the solutions of the fundamental equation
is a matrix of independent constants. Substituting each of the solutions of the fundamental equation  specifying the domain, we obtain by following the relation of the fundamental matrix, with the matrix of the system of equation (3.5)
specifying the domain, we obtain by following the relation of the fundamental matrix, with the matrix of the system of equation (3.5)
 (3.6)
(3.6)
If 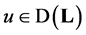 and domain of the operator 𝐋 defined by a system of equation (3.5), then for any
and domain of the operator 𝐋 defined by a system of equation (3.5), then for any  rightly the equality
rightly the equality
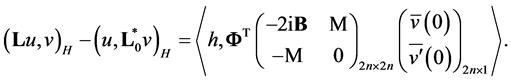
Element 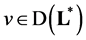 satisfies condition
satisfies condition
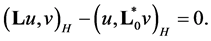 (3.7)
(3.7)
Let 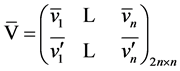 -basis in the linear
-basis in the linear  then each column of matrix
then each column of matrix 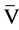 satisfies
satisfies
(3.7), and therefore
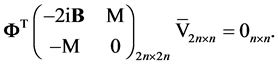 (3.8)
(3.8)
Of (3.6) and (3.8), it follows that the matrix 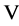 can be selected
can be selected 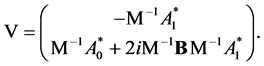
The operator 𝐋 is self-adjoint if and only if 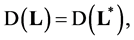 so if
so if 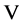 -matrix of the columns of the basis vectors in the subspace
-matrix of the columns of the basis vectors in the subspace 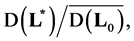 then
then 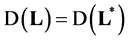 if and only if
if and only if 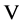 is also the matrix of the columns of the basis vectors in the subspace
is also the matrix of the columns of the basis vectors in the subspace 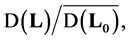 that is, any of its column satisfies the system of equation (3.5). And this is equivalent to the system of equations
that is, any of its column satisfies the system of equation (3.5). And this is equivalent to the system of equations

which proves Theorem 3.
4. Graph with Multiple Vertices
In the present article, a graph with multiple vertices is understood by one-dimensional cellular of complex [3]. Let graph Γ, be a collection of ![]() vertices
vertices  from each of which proceeds
from each of which proceeds 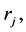
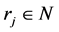 edges
edges 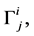 representing the infinity semidirect or line segments that connect vertex
representing the infinity semidirect or line segments that connect vertex 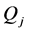 with other vertices. We fix on each edges
with other vertices. We fix on each edges 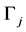 parametrization of the natural parameters. In this case, the edges of semidirect parameter increases from the boundary points and the edges of intervals, the orientation is chosen arbitrarily. Let
parametrization of the natural parameters. In this case, the edges of semidirect parameter increases from the boundary points and the edges of intervals, the orientation is chosen arbitrarily. Let 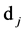 -initial point of the edges semidirect,
-initial point of the edges semidirect, 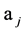 -initial point of edges
-initial point of edges  interval,
interval, 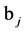 -end point of edges
-end point of edges 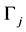 interval. Let
interval. Let  -the collection of all boundary points of the edges
-the collection of all boundary points of the edges 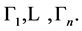 We define the function
We define the function ![]() on the set
on the set 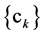 so that
so that  if
if  -beginning of edges and
-beginning of edges and 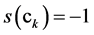 if
if 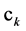 -end of the edges, denoted by
-end of the edges, denoted by ![]() diagonal matrix with numbers
diagonal matrix with numbers 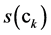 on the diagonal.
on the diagonal.
We introduce the operators 
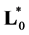 and the space
and the space 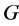 of boundary values of functions from
of boundary values of functions from 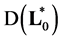 and their derivatives, linearly isomorphic to space
and their derivatives, linearly isomorphic to space 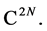 Through
Through  we denote the collection limit function values on edges of the boundary, which is the point
we denote the collection limit function values on edges of the boundary, which is the point 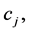 and by
and by 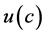 denote by
denote by 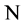 -dimensional vector of
-dimensional vector of 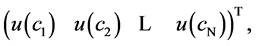 for the vector limit values of the derivative
for the vector limit values of the derivative 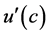 use similar notation, and let
use similar notation, and let 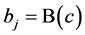 denoted in
denoted in 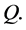
Theorem 4. Let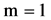 ,
,  and
and  The operator 𝐋 with domain
The operator 𝐋 with domain

adjoint if and only if the matrix 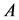 satisfies the equality
satisfies the equality 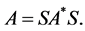
Proof. If 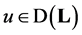 and
and 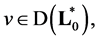 then we have the equality
then we have the equality
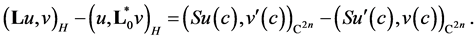
Hence

Traces 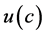 take arbitrary values, therefore the equality
take arbitrary values, therefore the equality 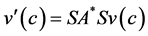 is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 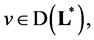 which proves Theorem 4.
which proves Theorem 4.
Corollary 2. If  and
and 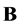 -diagonal matrices and the matrix elements are defined by the formula
-diagonal matrices and the matrix elements are defined by the formula
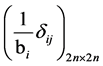

 respectively, and
respectively, and 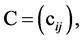 where
where 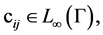 then the operator
then the operator
𝐋 with domain 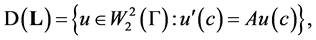 self-adjoint if and only if the matrices
self-adjoint if and only if the matrices 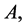
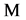 and
and 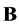 satisfy the equality
satisfy the equality 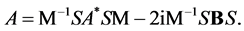
Proof. If 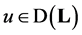 and
and 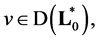 then we have the equality
then we have the equality
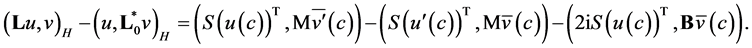
Hence
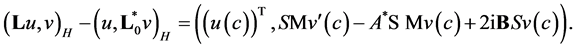
Traces 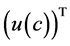 take arbitrary values, therefore the equality
take arbitrary values, therefore the equality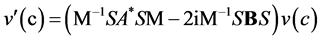 is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 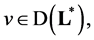 which proves the corollary 2.
which proves the corollary 2.
5. Graph with One Vertex and with a Countable Set of Rays
description of this graph is defined by the following structures [11]. In this case we denote by  -locally finite non-negative countably additive measure on N such that
-locally finite non-negative countably additive measure on N such that 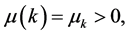 denoted by
denoted by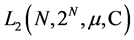 —Hilbert space of boundary values with the norm
—Hilbert space of boundary values with the norm
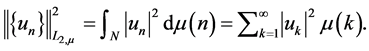
The restriction of any function on semidirect possesses the boundary values at the vertex:
 This is also true for the first derivatives of these restrictions
This is also true for the first derivatives of these restrictions 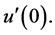 We denote by
We denote by 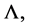
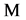 and
and 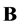 diagonal matrices and their matrix elements are given by the formula
diagonal matrices and their matrix elements are given by the formula 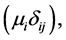
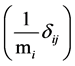 and
and  respectively.
respectively.
Theorem 5. Let 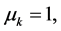
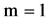 ,
, 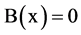 and
and 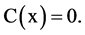 The operator
The operator  with domain
with domain
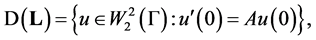 self-adjoint if and only if the operator
self-adjoint if and only if the operator 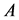 is self-adjoint in the space
is self-adjoint in the space 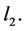
Proof. If 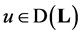 and
and  then we have the equality
then we have the equality
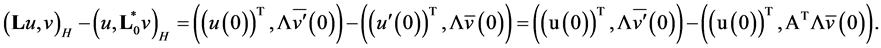
Hence 
Traces  take arbitrary values in the space
take arbitrary values in the space  therefore the equality
therefore the equality
 is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 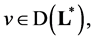 which proves Theorem 5.
which proves Theorem 5.
Corollary 3. If 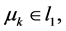
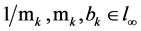 and
and 
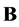 and
and 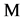 are operators in the space
are operators in the space  given by diagonal matrices with elements
given by diagonal matrices with elements 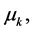

 on the diagonal, respectively,
on the diagonal, respectively, 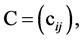 where
where
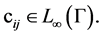 Then the operator
Then the operator 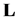 with domain
with domain 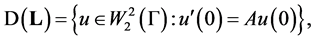 self-adjoint if and only if the operators
self-adjoint if and only if the operators 
 and
and 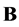 acting in the space
acting in the space 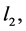 satisfy the equality
satisfy the equality
 (5.1)
(5.1)
Proof. If 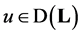 and
and  then we have the equality
then we have the equality
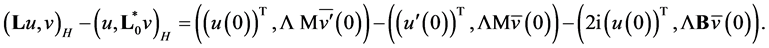
Hence 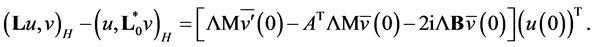
Traces 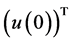 take arbitrary values in the space
take arbitrary values in the space 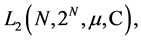 therefore the equality
therefore the equality
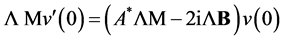 is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 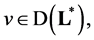 as
as  if and only if
if and only if 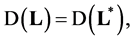 then for the self-adjoint operator
then for the self-adjoint operator 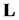 is necessary and sufficient to satisfy the equality (5.1).
is necessary and sufficient to satisfy the equality (5.1).
6. Schrödinger Operators on Branched Manifolds
The assumption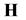 . Let the function m takes the constant values
. Let the function m takes the constant values 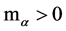 on each region
on each region 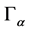 for all
for all
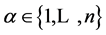 , and satisfy condition
, and satisfy condition 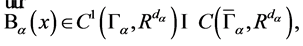
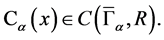 Through
Through  we denote the limiting values of the vector function
we denote the limiting values of the vector function 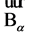 on the boundary
on the boundary 
The operator 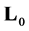 with domain
with domain 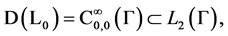 densely defined and symmetric. The domain
densely defined and symmetric. The domain
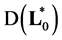 adjoint operator
adjoint operator 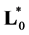 is a linear subspace
is a linear subspace 
Let the components 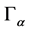 manifold
manifold ![]() constitute a
constitute a ![]() semidirect,
semidirect, ![]() finite intervals and
finite intervals and 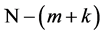 regions. In the case of one-dimensional region
regions. In the case of one-dimensional region 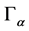 boundary value
boundary value 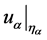 is a set of complex numbers on the boundary
is a set of complex numbers on the boundary 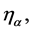 represents one or two points. In the case
represents one or two points. In the case 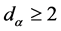 boundary value
boundary value 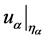 is an element of the space
is an element of the space 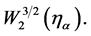 According to the trace theorem
According to the trace theorem 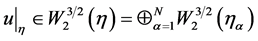 ([12]). Through
([12]). Through  denote the collection of
denote the collection of  limit values function
limit values function ![]() on the boundary
on the boundary  Similarly, the limit value of the derivative
Similarly, the limit value of the derivative 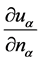 constriction
constriction 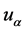 in the direction of the outer normal
in the direction of the outer normal 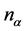 to boundary
to boundary  in the case semidirect
in the case semidirect 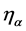 represents a an element of space
represents a an element of space , in case of a limited interval-element of space
, in case of a limited interval-element of space 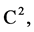 and in the case of dimension
and in the case of dimension 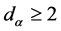 -element of space
-element of space 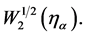
The boundary values of the normal derivative is denoted by 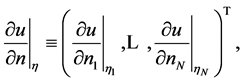 where
where  is vector of the external relative to
is vector of the external relative to  normal to the
normal to the 
We introduce the Hilbert space

We define space of boundary values 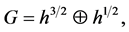 where
where 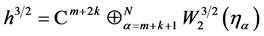 and similarly,
and similarly, 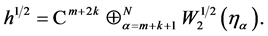
Boundary value  function
function 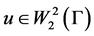 is an element of the space
is an element of the space 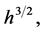 and the boundary value
and the boundary value 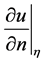 its normal derivative-an element of the space
its normal derivative-an element of the space 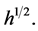
We introduce in the space ![]() operators
operators 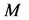 and
and  Operator
Operator 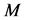 acts on each element
acts on each element 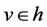 as an operator of multiplication by a function
as an operator of multiplication by a function
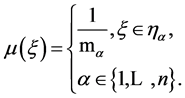
And operator  acts on each element
acts on each element 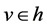 as an operator of multiplication by a function
as an operator of multiplication by a function
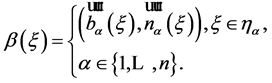
Theorem 6. Let performed assumption 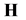 about functions
about functions 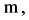
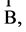
![]() and
and 
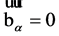 for any
for any 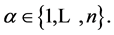 Let
Let 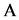 -linear operator in space
-linear operator in space ![]() with a dense domain
with a dense domain 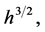 the values of which belongs in linear manifold
the values of which belongs in linear manifold 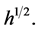 Let
Let 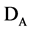 -linear manifold of functions
-linear manifold of functions 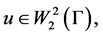 boundary values are related to the boundary values of the derivatives in the direction of the outward normal by relation
boundary values are related to the boundary values of the derivatives in the direction of the outward normal by relation
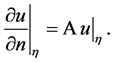
Then the self-adjoint operator 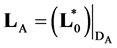 is necessary and sufficient to satisfy the equality
is necessary and sufficient to satisfy the equality 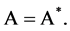
Proof. Since 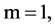
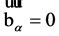 for any
for any 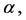 then from conditions
then from conditions 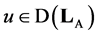 and
and 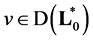 then we have the equality
then we have the equality
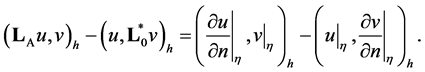
Hence
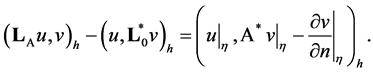
Traces  take arbitrary values, therefore the equality
take arbitrary values, therefore the equality  is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 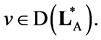 Since the domain of definition operator
Since the domain of definition operator  is determined by the equation
is determined by the equation 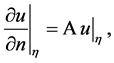
that 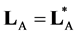 then implies that
then implies that 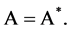
Corollary 4. Let performed assumption 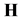 about functions
about functions 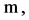
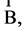
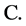 Let
Let 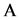 -linear operator in space
-linear operator in space ![]() with a dense domain
with a dense domain 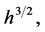 the values of which belongs in linear manifold
the values of which belongs in linear manifold 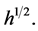 Let
Let 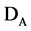 -linear manifold of functions
-linear manifold of functions 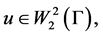 boundary values are related to the boundary values of the derivatives in the direction of the outward normal by relation
boundary values are related to the boundary values of the derivatives in the direction of the outward normal by relation
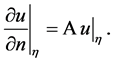
Then the self-adjoint operator  is necessary and sufficient to satisfy the equality
is necessary and sufficient to satisfy the equality 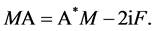
Proof. Since performed assumption 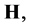 then from conditions
then from conditions  and
and  then we have the equality
then we have the equality
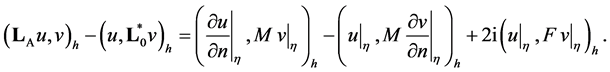
Hence
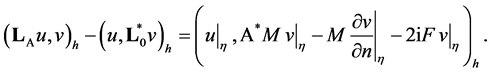
Traces 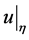 take arbitrary values, therefore the equality
take arbitrary values, therefore the equality 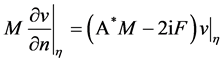 is necessary and sufficient for inclusion
is necessary and sufficient for inclusion 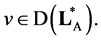 Since the domain of definition operator
Since the domain of definition operator 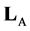 is determined by the equation
is determined by the equation 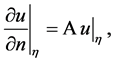
that 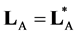 then implies that
then implies that 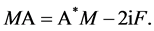
7. Conclusion
In this paper we describe the set of all Schrödinger operators on graph and branched manifold, defined as a self-adjoint extension of the operator, originally defined on smooth functions with supports, not contained in the branch points manifold. Thus, given a description of the various options, we determine the Laplace operator on the space of the functions defined on a branched manifold. Description of the definition of each of the self-adjoint extensions is given in terms of linear relations satisfied by the limit at the branch points and the boundary points of the graph function value in the domain of operator and the its derivative. Each of the Laplace operators corresponds to the Markov process, whose behavior in a neighborhood of branch points, we determined by the choice of the domain of the Laplace operator, obtained in this paper results, which is an extension of the study work [8] describes the self-adjoint extensions of a graph with a single vertex and two edges, to the case of a graph with an arbitrary number of edges. In addition, this paper summarizes the results of [6] in the case of Laplace operators, for which the linear relation in the space of boundary values that define the domain of the operator, do not admit the possibility of expressing the limit function values at the boundary points and branch points of the graph of the limiting values of its derivative.
REFERENCES
- Y. V. Pokorny, O. M. Penkin, V. L. Pryadier, A. V. Borovskikh, K. P. Lazarev and S. A. Shabrov, “Differential Equations on Geometric Graphs,” M. FIZMATLIT, 2004.
- V. L. Chernyshev and A. I. Shafarevich, “Semiclassical Spectrum of the Schrödinger Operator on a Geometric Graph,” Mathematical Notes, Vol. 82, No. 3-4, 2007, pp. 542-554. http://dx.doi.org/10.1134/S0001434607090313
- O. M. Penkin and Y. V. Pokornyi, “On Some Qualitative Properties of Equations for the One-Dimensional CW-complex,” Mathematical Notes, Vol.59, No. 5, 1996, pp. 562-565. http://dx.doi.org/10.1007/BF02308827
- A. A. Tolchennikov, V. L. Chernyshev and A. I. Shafarevich, “Asymptotic Properties and Classical Dynamical Systems in Quantum Problems on Singular Spaces,” Nelineinaya Dinamika, Vol. 6, No. 3, 2010, pp. 623-638.
- G. G. Amosov and V. Z. Sakbaev, “On Self-Adjoint Extensions of Schrödinger Operators Degenerating on a Pair of Half-Lines and the Corresponding Markovian Cocycles,” Mathematical Notes, Vol. 76, No. 3, 2004, pp. 315-322. http://dx.doi.org/10.1023/B:MATN.0000043458.91218.7b
- V. Z. Sakbaev and O. G. Smolyanov, “Dynamics of a Quantum Particle with Discontinuous Position-Dependent Mass,” Doklady Mathematics, Vol. 82, No. 1, 2010, pp. 630-633. http://dx.doi.org/10.1134/S1064562410040332
- V. Z. Sakbaev and O. G. Smolyanov, “Diffusion and Quantum Dynamics on Graphs,” Doklady Mathematics, Vol. 88, No. 1, 2013, pp. 404-408. http://dx.doi.org/10.1134/S1064562413040108
- M. Gadella, S. Kuru and J. Negro, “Self-Adjoint Hamiltonians with a Mass Jump: General Matching Conditions,” Physics Letters A, 2007, Vol. 362, No. 4, pp. 265-268. http://dx.doi.org/10.1016/j.physleta.2006.10.029
- M. Reed and B. Simon, “Methods of Modern Mathematical Physics ‘1. Functional Analysis’,” Academic Press, New York London, 1972.
- T. Kato, “Perturbation Theory for Linear Operators,” Springer-Verlag, Berlin, Heidelberg, New York, 1966.
- N. Dunford and J. T. Schwartz, “Linear Operators ‘Part I: General Theory’,” Interscience Publishers, New York, London, 1958.
- G. N. Jakovlev, “Traces of Functions in the Space
 on Piecewise Smooth Surfaces,” Mathematics of the USSR-Sbornik, Vol. 3, No. 4, 1967, pp. 481-497. http://dx.doi.org/10.1070/SM1967v003n04ABEH002758
on Piecewise Smooth Surfaces,” Mathematics of the USSR-Sbornik, Vol. 3, No. 4, 1967, pp. 481-497. http://dx.doi.org/10.1070/SM1967v003n04ABEH002758

