Journal of Applied Mathematics and Physics
Vol.1 No.7(2013), Article ID:40715,4 pages DOI:10.4236/jamp.2013.17001
An Optimal Double Inequality among the One-Parameter, Arithmetic and Geometric Means
College of Mathematics and Computer Science, Hebei University, Baoding, China
Email: ghy@hbu.cn, 563211828@qq.com, 347764565@qq.com, 602580999@qq.com
Copyright © 2013 Hongya Gao et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 12, 2013; revised November 12, 2013; accepted November 17, 2013
Keywords: Optimal Double Inequality; One-Parameter Mean; Arithmetic Mean; Geometric Mean
ABSTRACT
In the present paper, we answer the question: for 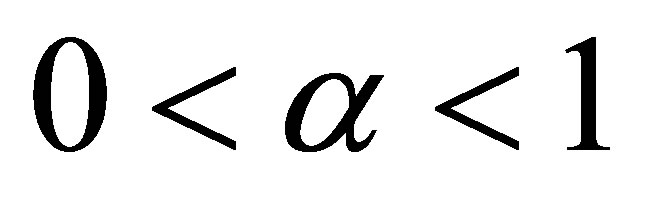 fixed, what are the greatest value
fixed, what are the greatest value 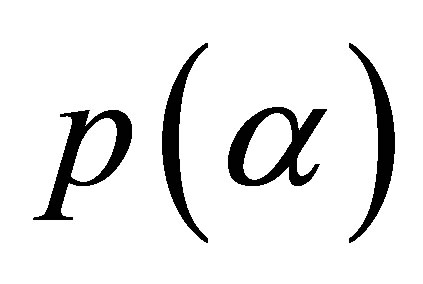 and the least value
and the least value 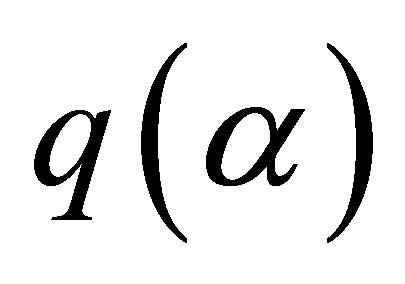 such that the double inequality
such that the double inequality  holds for all
holds for all 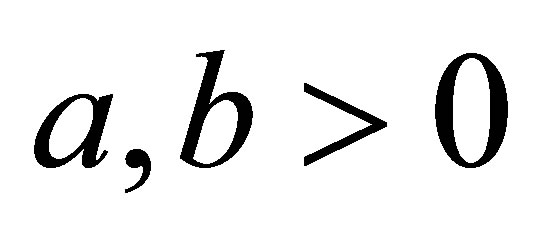 with
with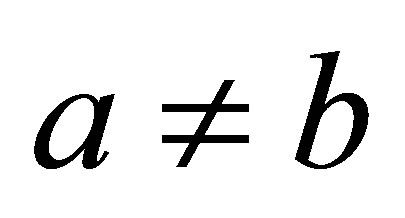 ? where for
? where for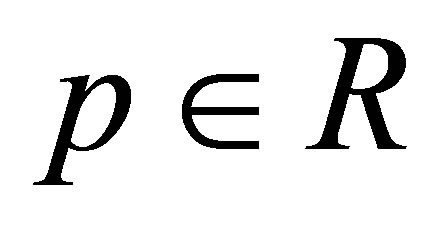 , the one-parameter mean
, the one-parameter mean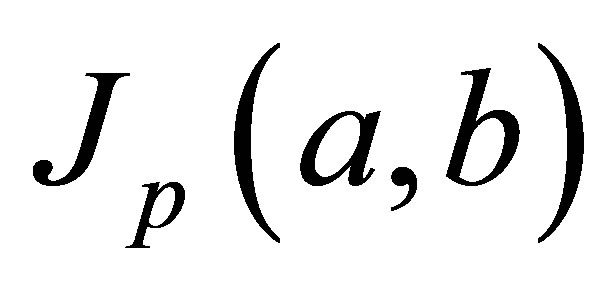 , arithmetic mean
, arithmetic mean  and geometric mean
and geometric mean 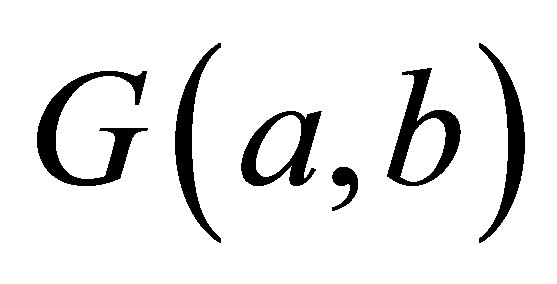 of two positive real numbers
of two positive real numbers  and
and 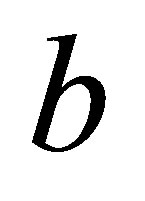 are defined by
are defined by 
 and
and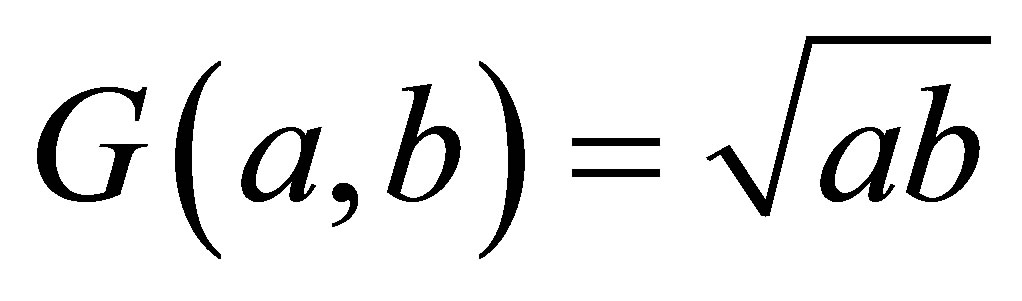 , respectively.
, respectively.
1. Introduction
For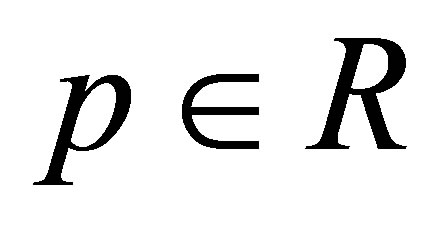 , the one-parameter mean
, the one-parameter mean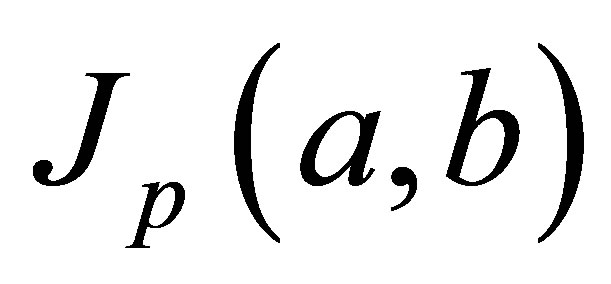 , arithmetic mean
, arithmetic mean 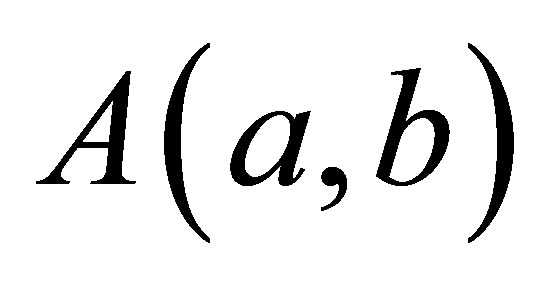 and geometric mean
and geometric mean 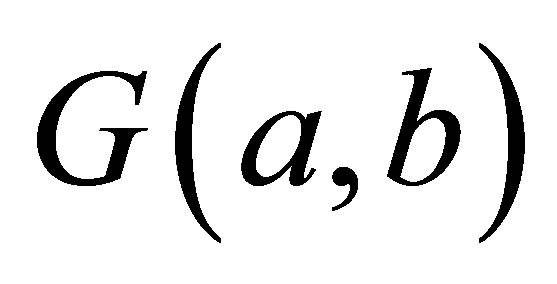 of two positive real numbers
of two positive real numbers  and
and  are defined by
are defined by
 (1)
(1)
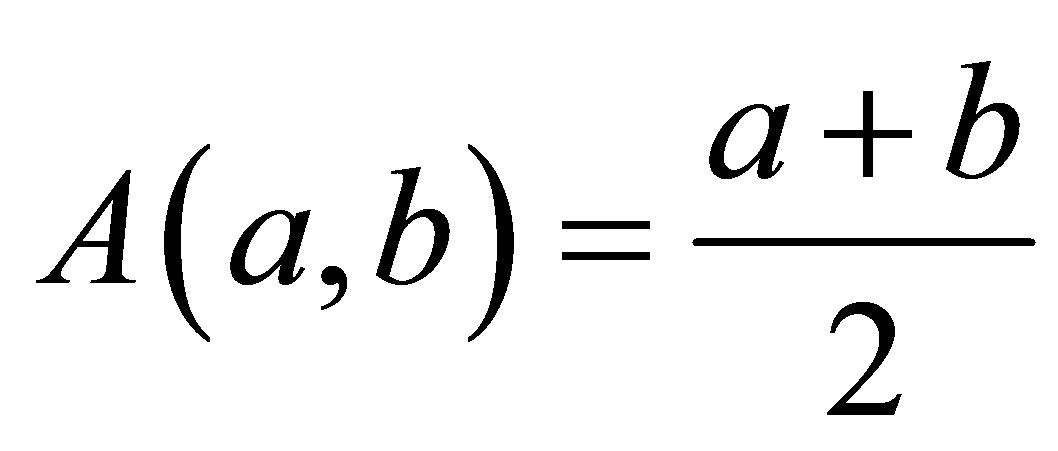 and
and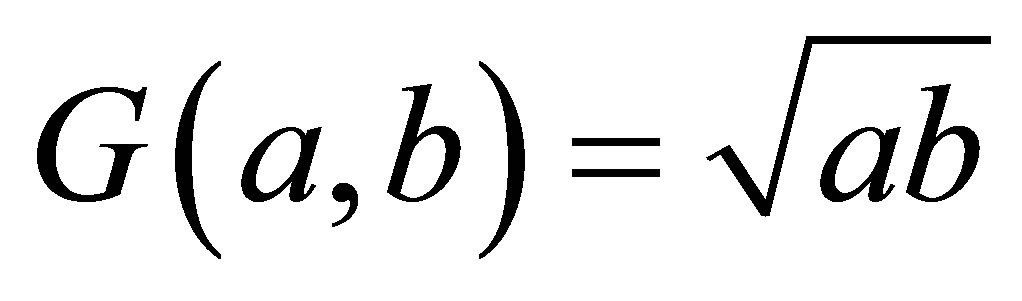 , respectively.
, respectively.
It is well-known that the one-parameter mean is continuous and strictly increasing with respect to 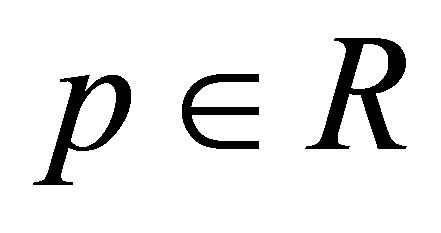 for fixed
for fixed 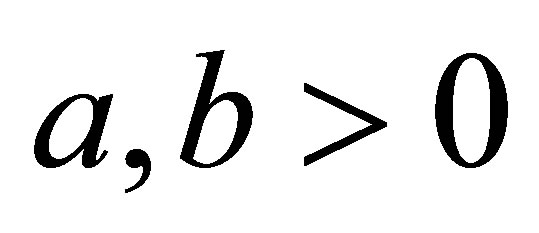 with
with . Many means are special cases of the one-parameter mean, for example:
. Many means are special cases of the one-parameter mean, for example:
 is the arithmetic mean,
is the arithmetic mean, 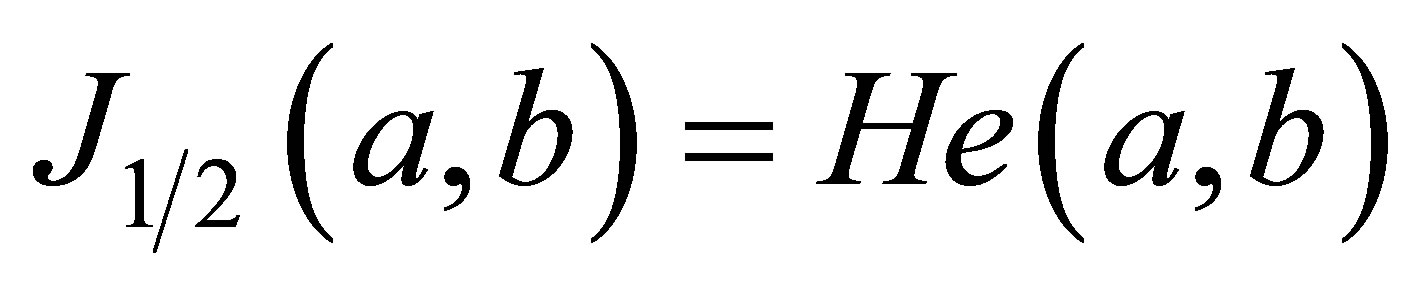 is the Heronian mean,
is the Heronian mean,  is the geometric mean, and
is the geometric mean, and 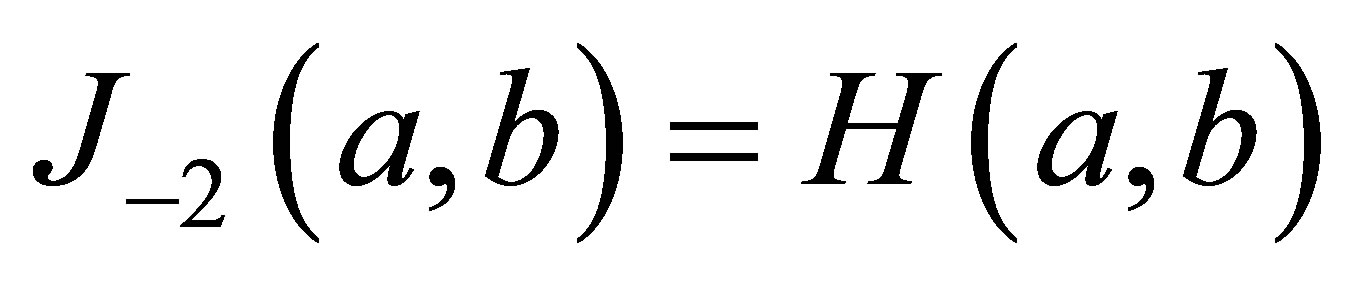 is the harmonic mean.
is the harmonic mean.
The one-parameter mean 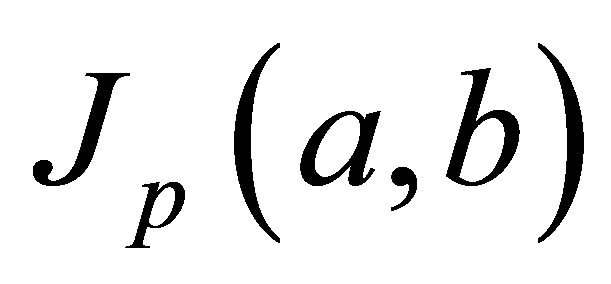 and its inequalities have been studied intensively, see [1-6].
and its inequalities have been studied intensively, see [1-6].
The purpose of this paper is to answer the question: for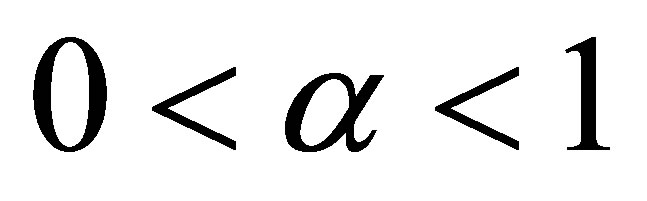 , what are the greatest value
, what are the greatest value 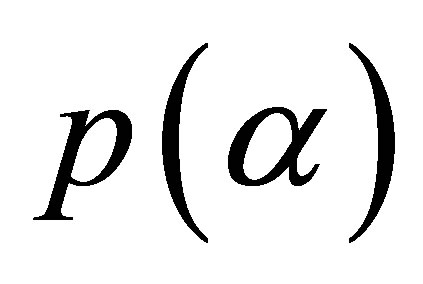 and the least value
and the least value 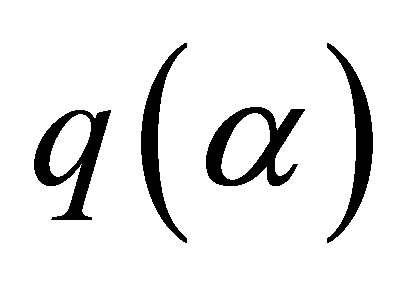 such that the double inequality
such that the double inequality
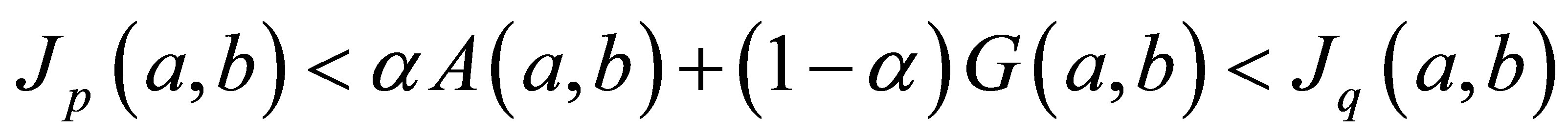 holds for all
holds for all 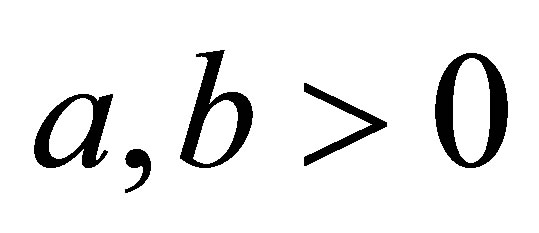 with
with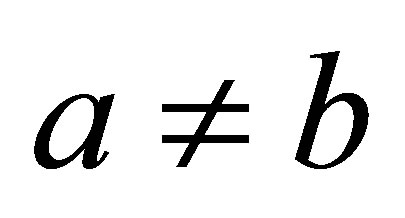 ?
?
2. Main Result
The main result of this paper is the following theorem.
Theorem 2.1. Let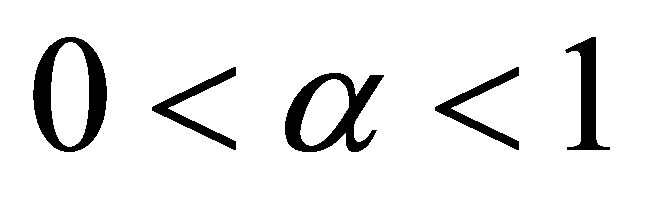 . Then for any
. Then for any 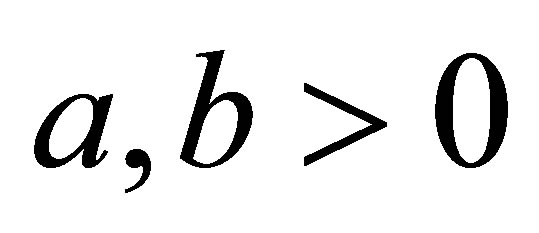 with
with , we have 1)
, we have 1)
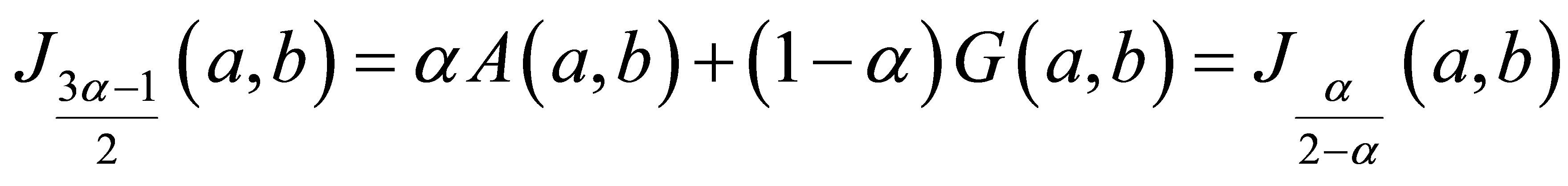 for
for 2)
2)
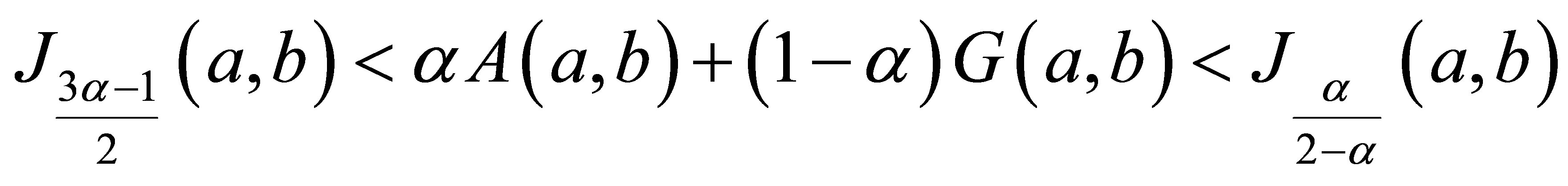 for
for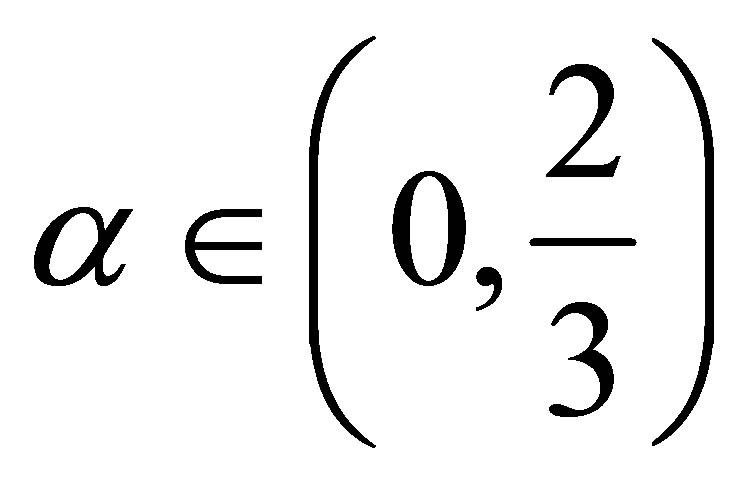 3)
3)
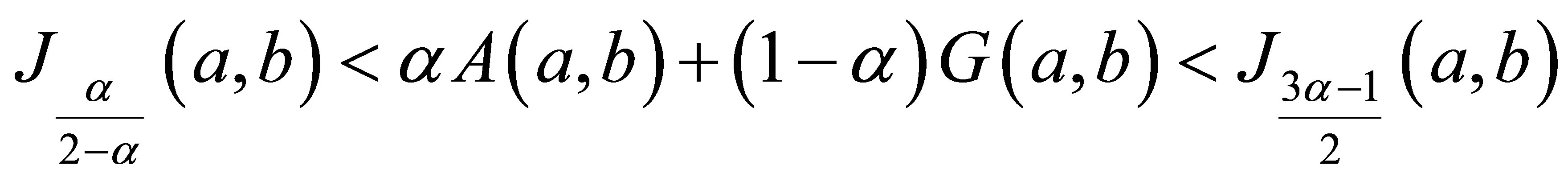 for
for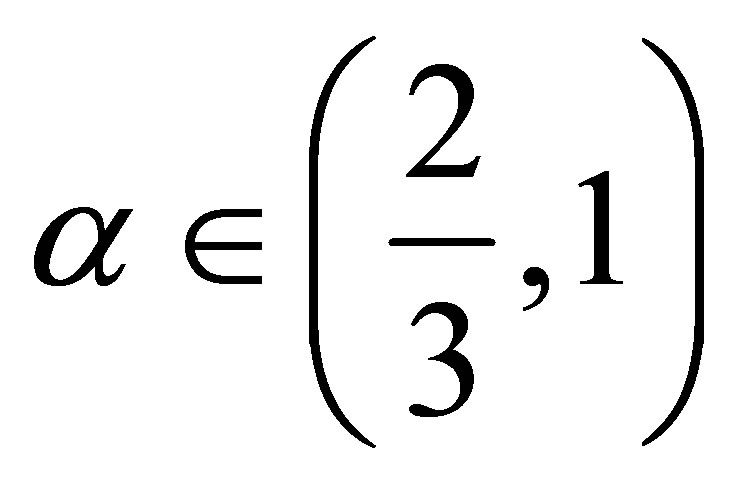 .
.
The numbers 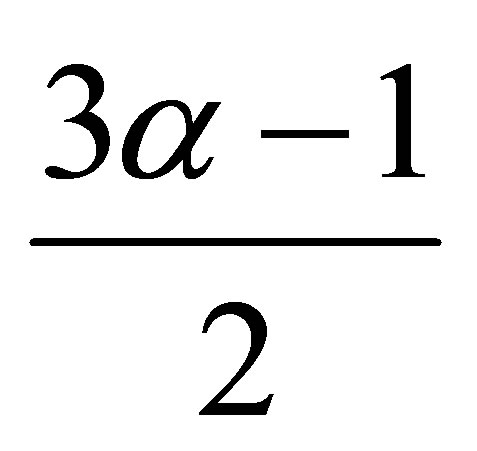 and
and 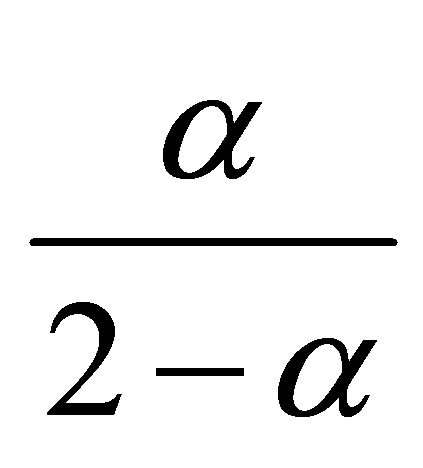 in 2) and 3) are optimal.
in 2) and 3) are optimal.
In order to prove Theorem 2.1, we need a preliminary lemma.
Lemma 2.1. For , one has
, one has
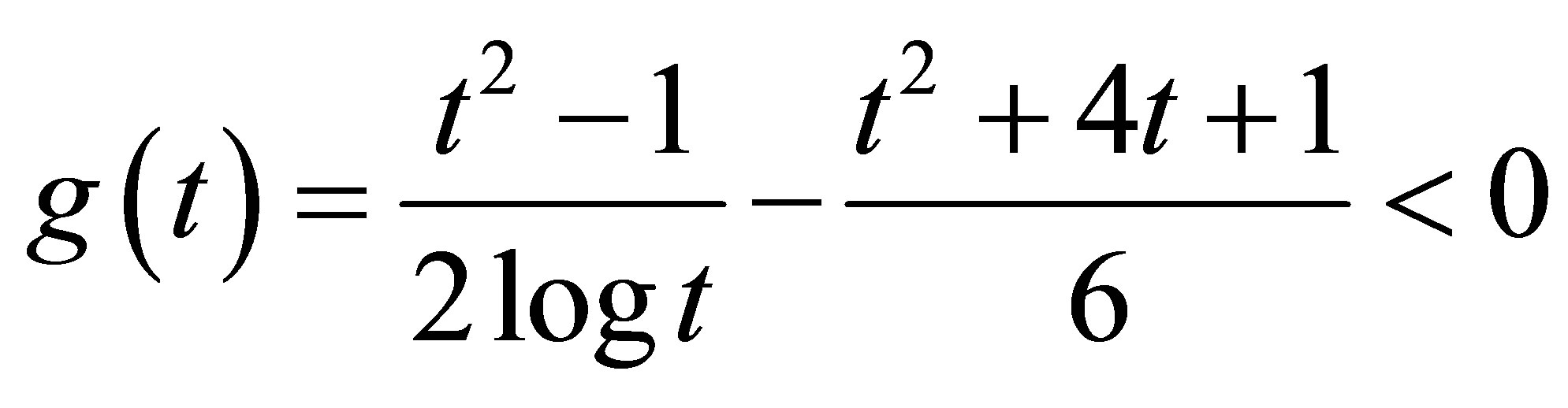 (2)
(2)
Proof. Simple calculations lead to
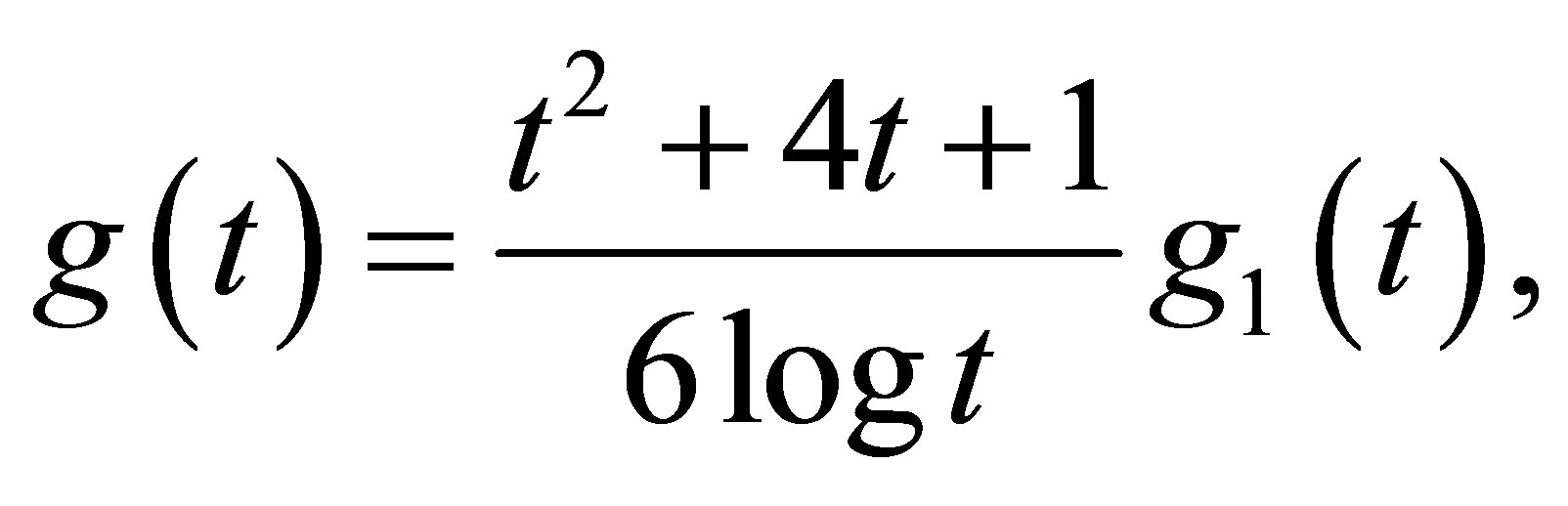 (3)
(3)
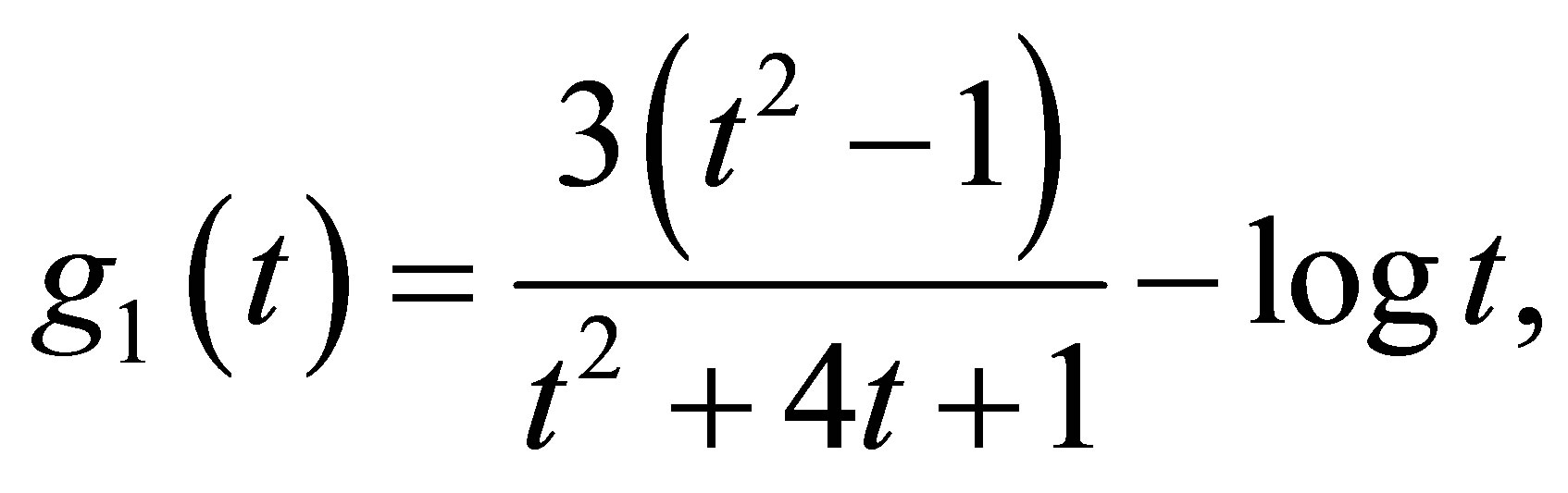 (4)
(4)
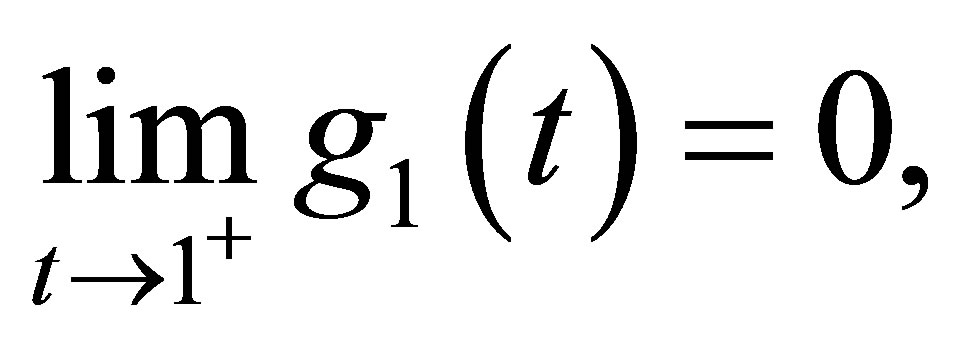 (5)
(5)
 (6)
(6)
(2) follows from (3)-(6).
Proof of Theorem 2.1. Without loss of generality we assume 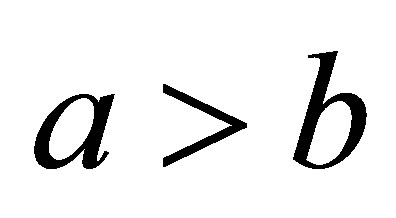 and take
and take  We first consider the case
We first consider the case . 1) follows from
. 1) follows from
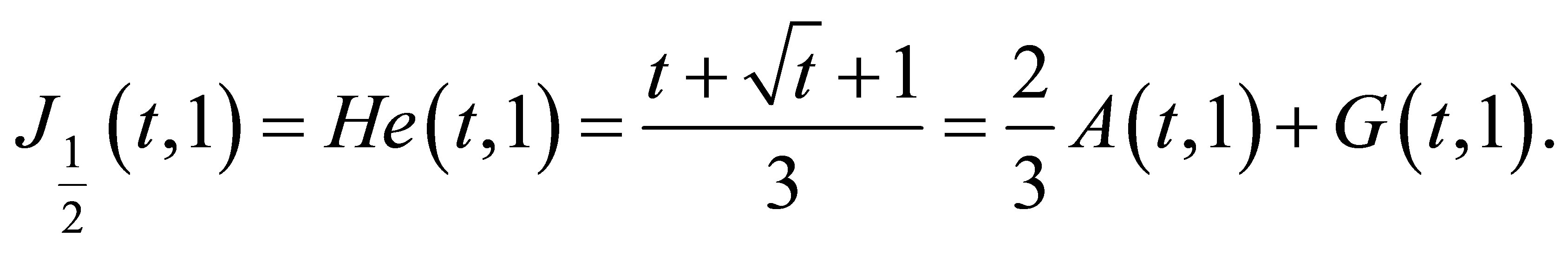
From now on we assume  Let
Let  then (1) leads to
then (1) leads to
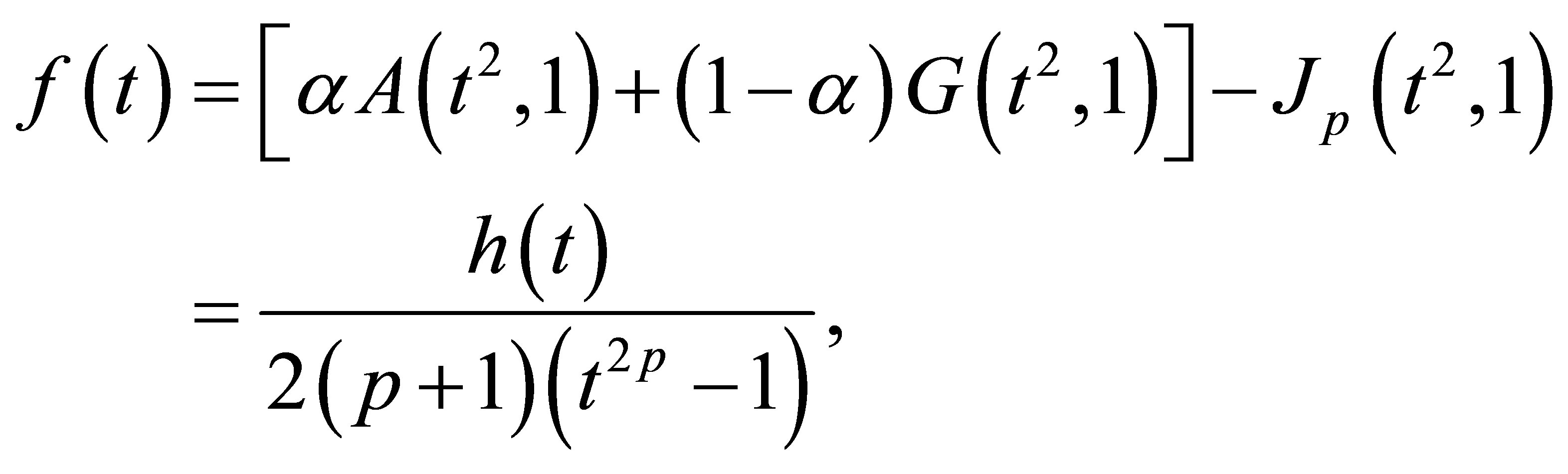 (7)
(7)
where
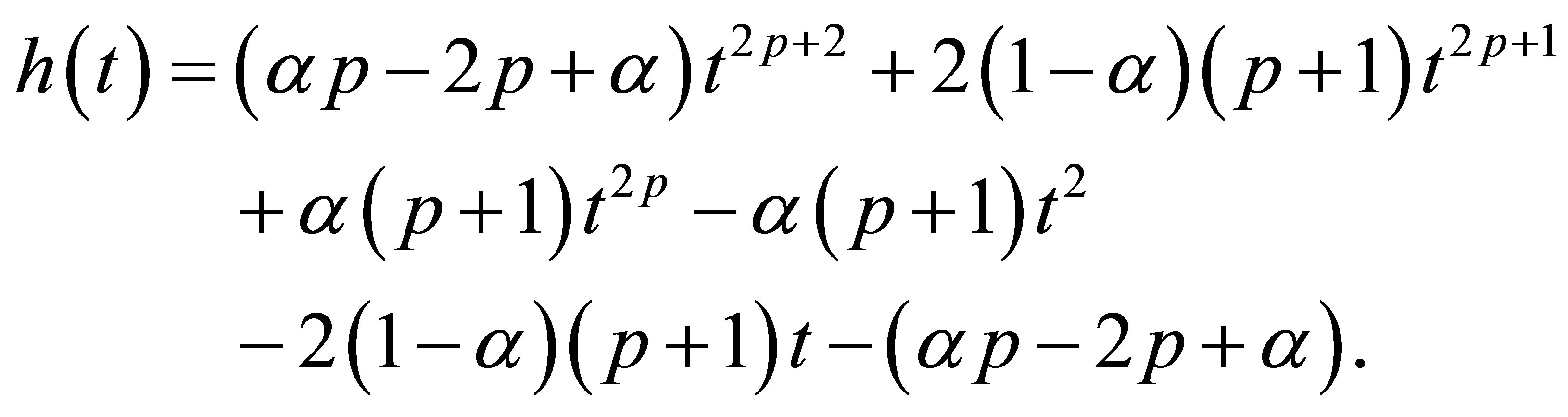
Simple calculations lead to
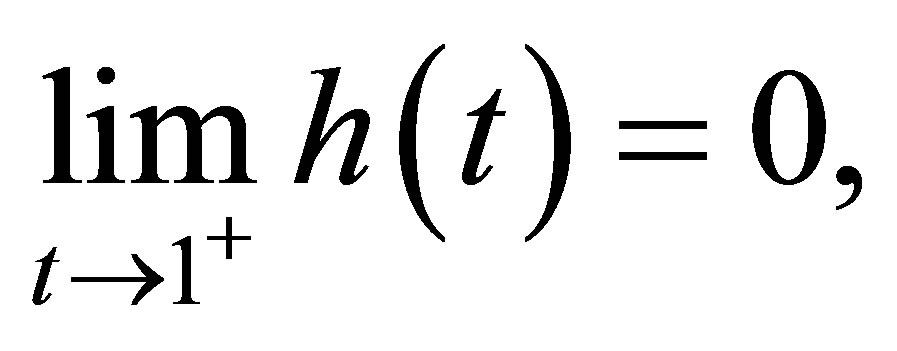 (8)
(8)
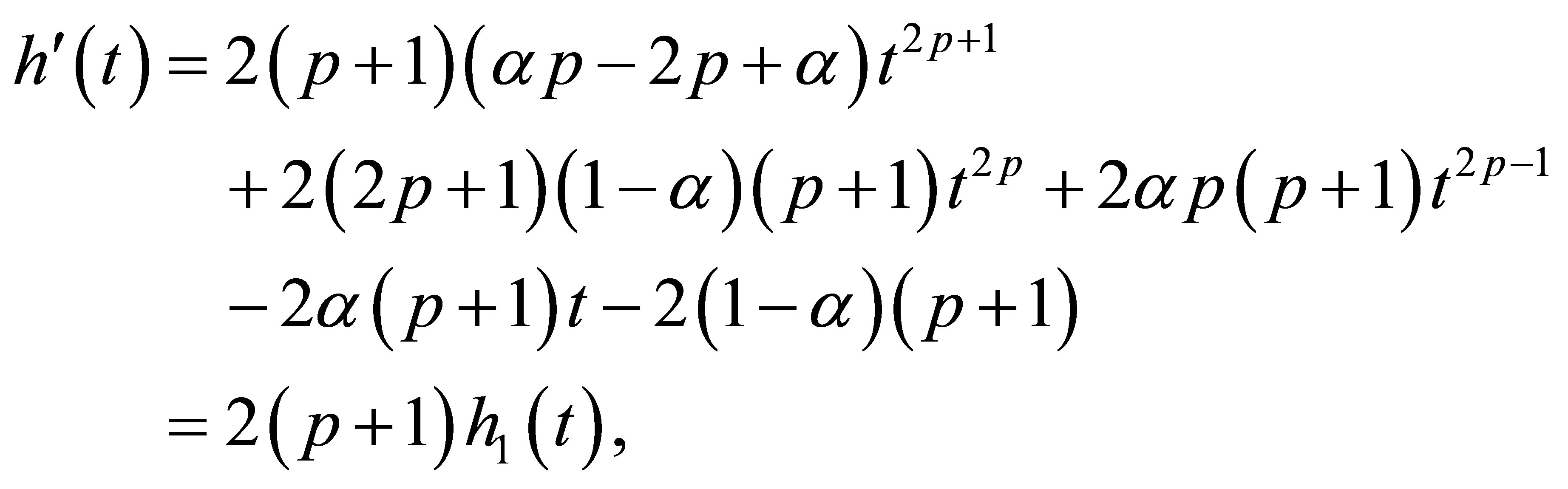
where
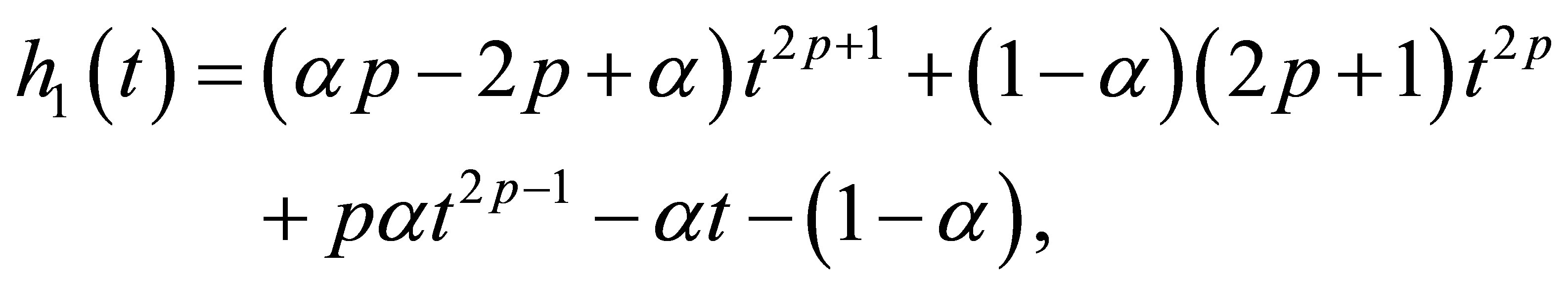
 (9)
(9)
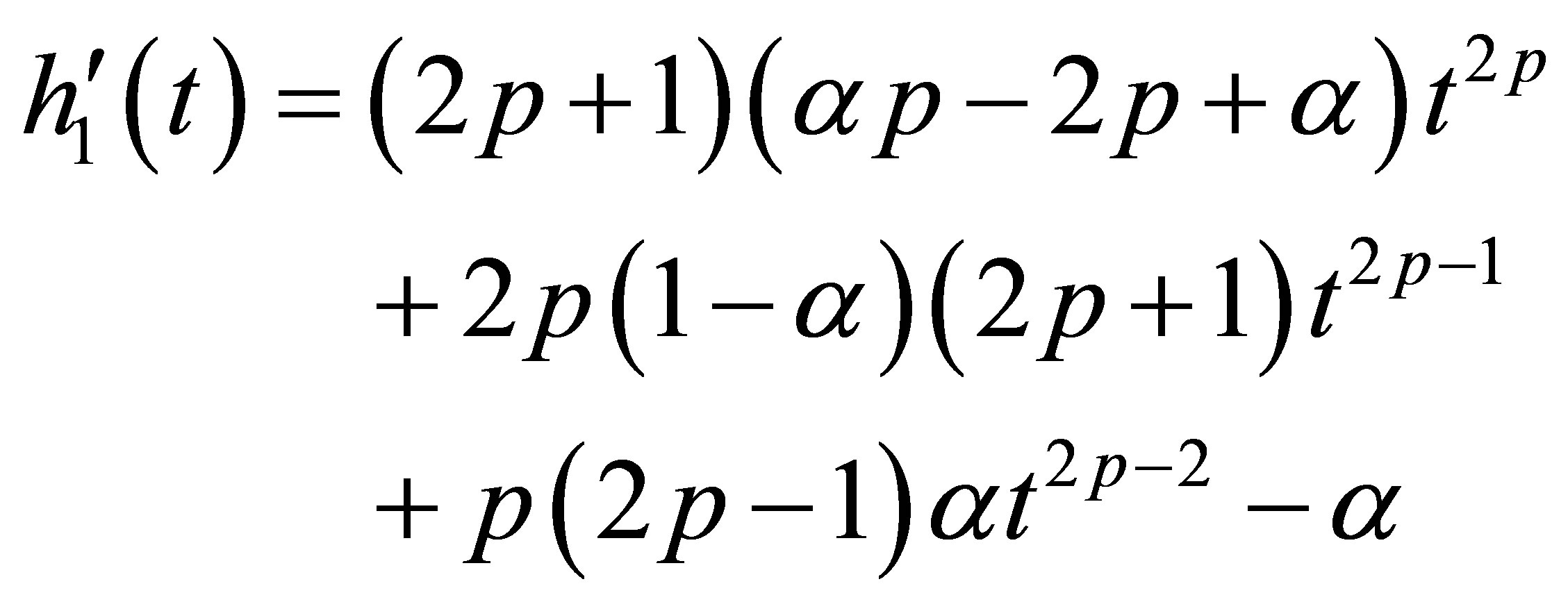
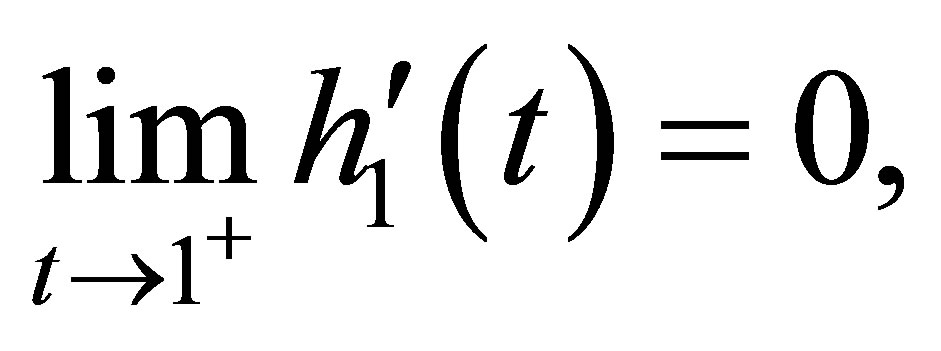 (10)
(10)
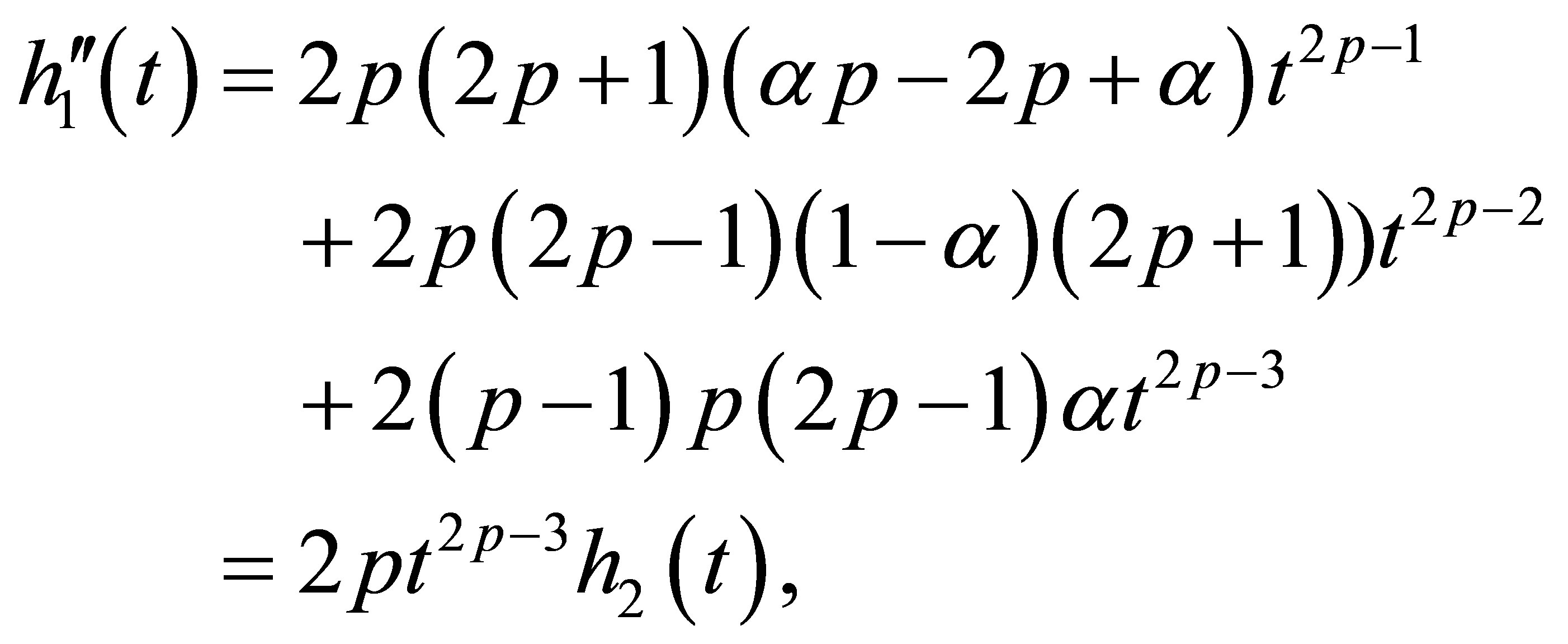 (11)
(11)
where
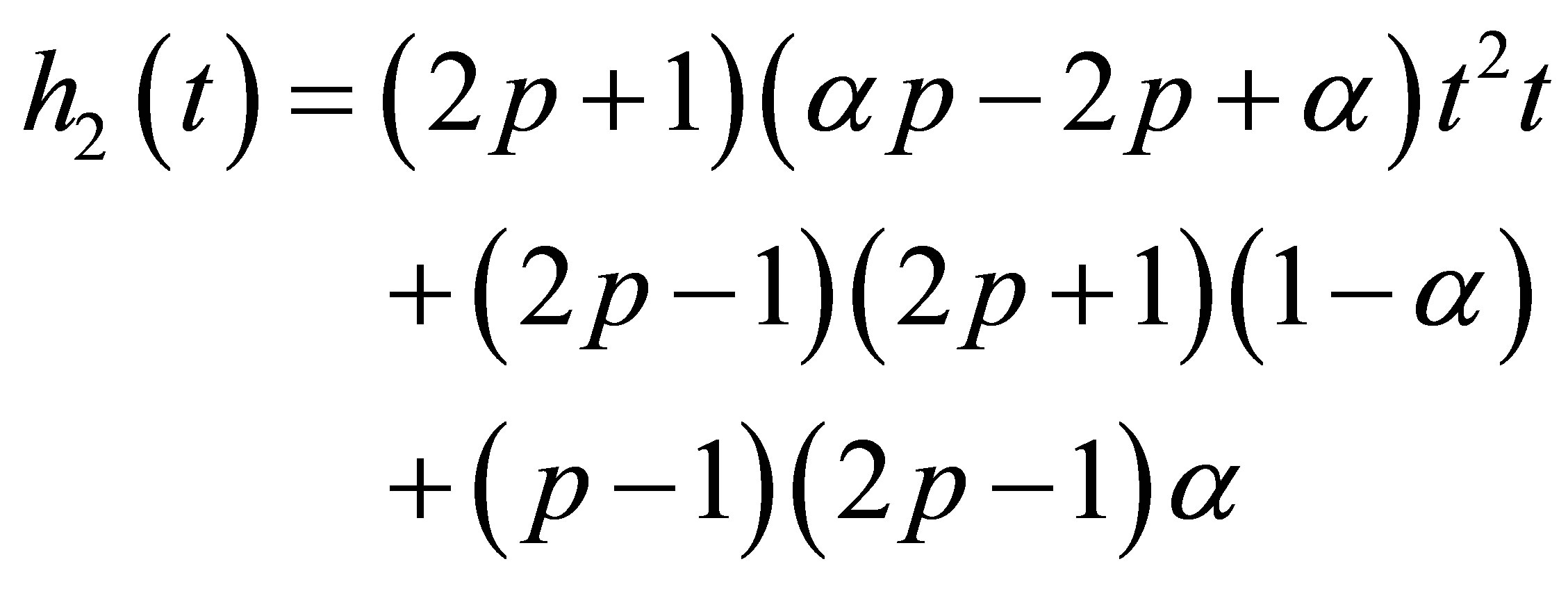
 (12)
(12)
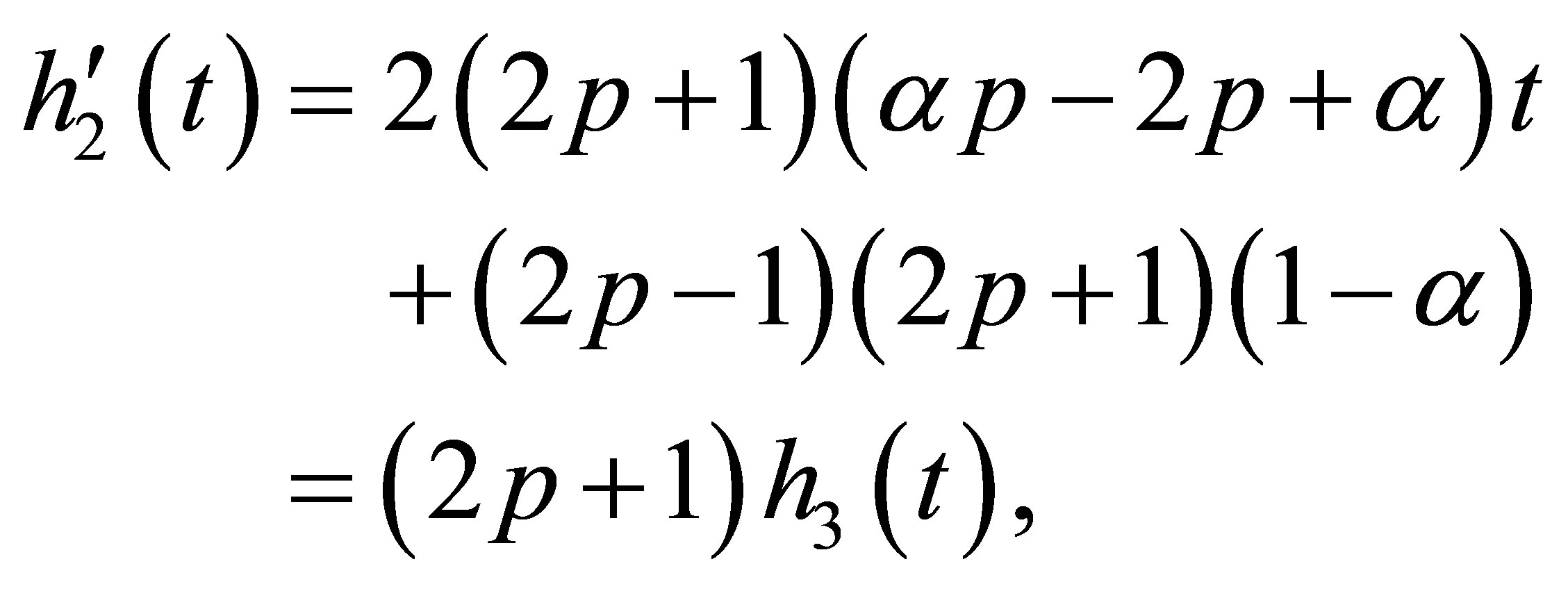 (13)
(13)
where
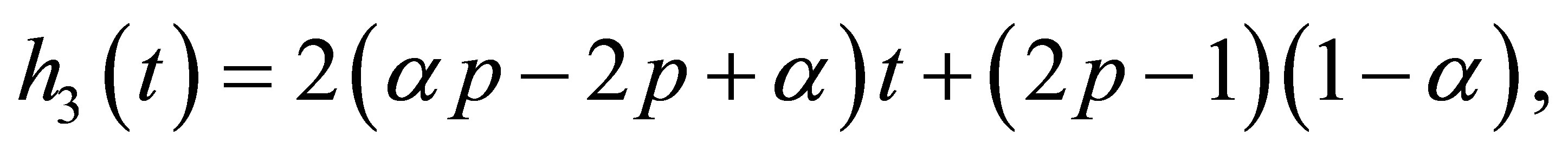 (14)
(14)
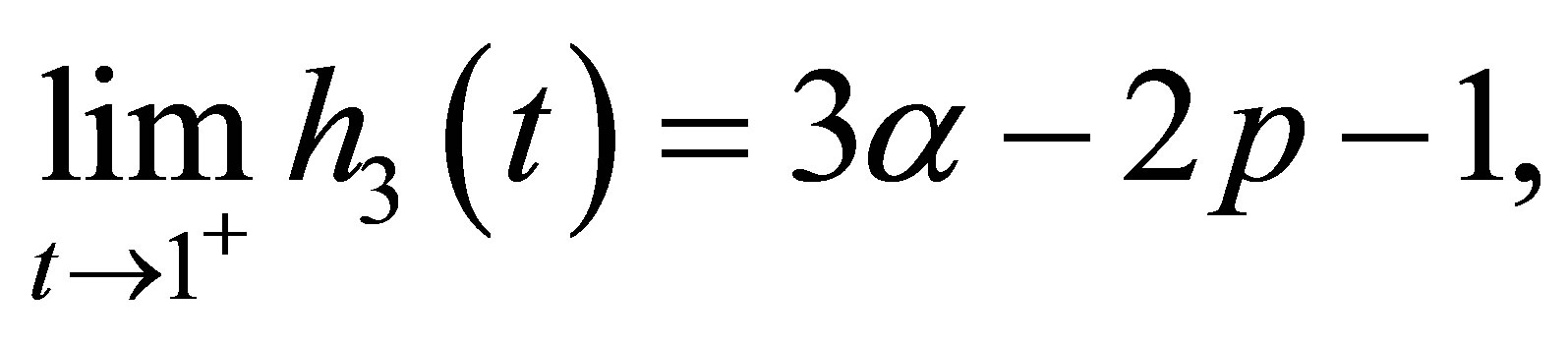 (15)
(15)
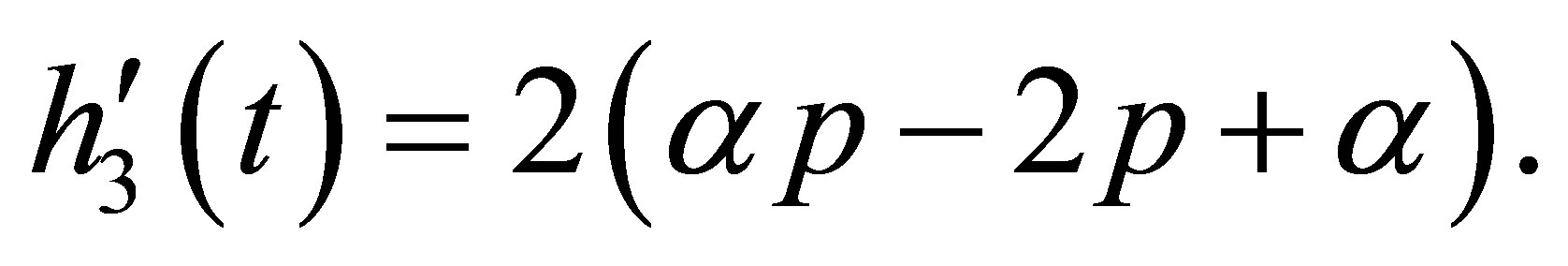 (16)
(16)
We shall distinguish between two cases.
Case 1.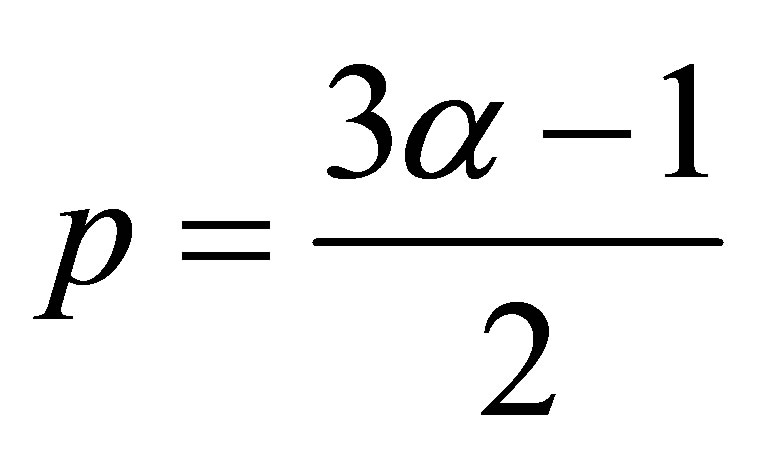 . The left-hand side inequality of 2)
. The left-hand side inequality of 2)
for  follows from Lemma 2.1 because in this case
follows from Lemma 2.1 because in this case
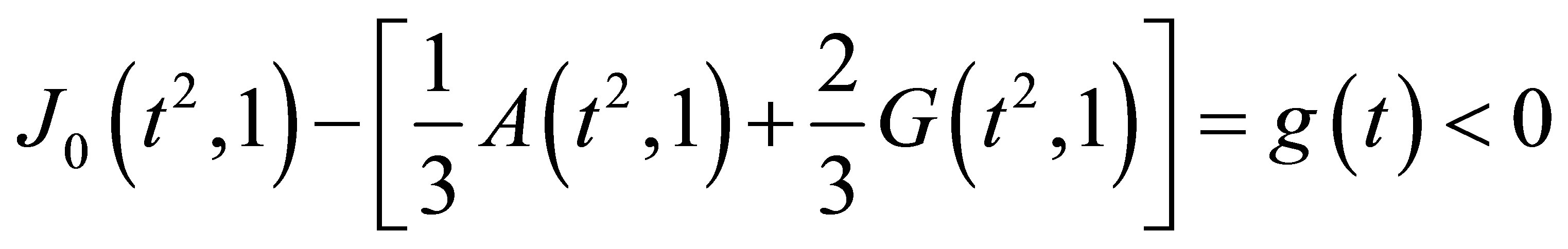
for all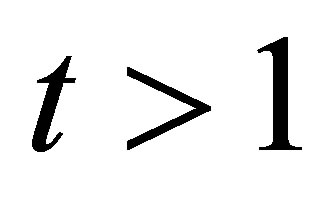 . In the sequel we assume
. In the sequel we assume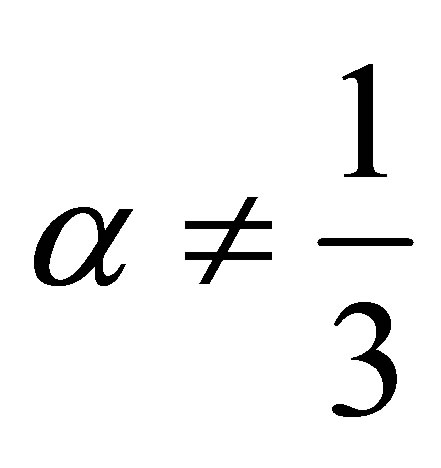 .
.
We clearly see from (16) that
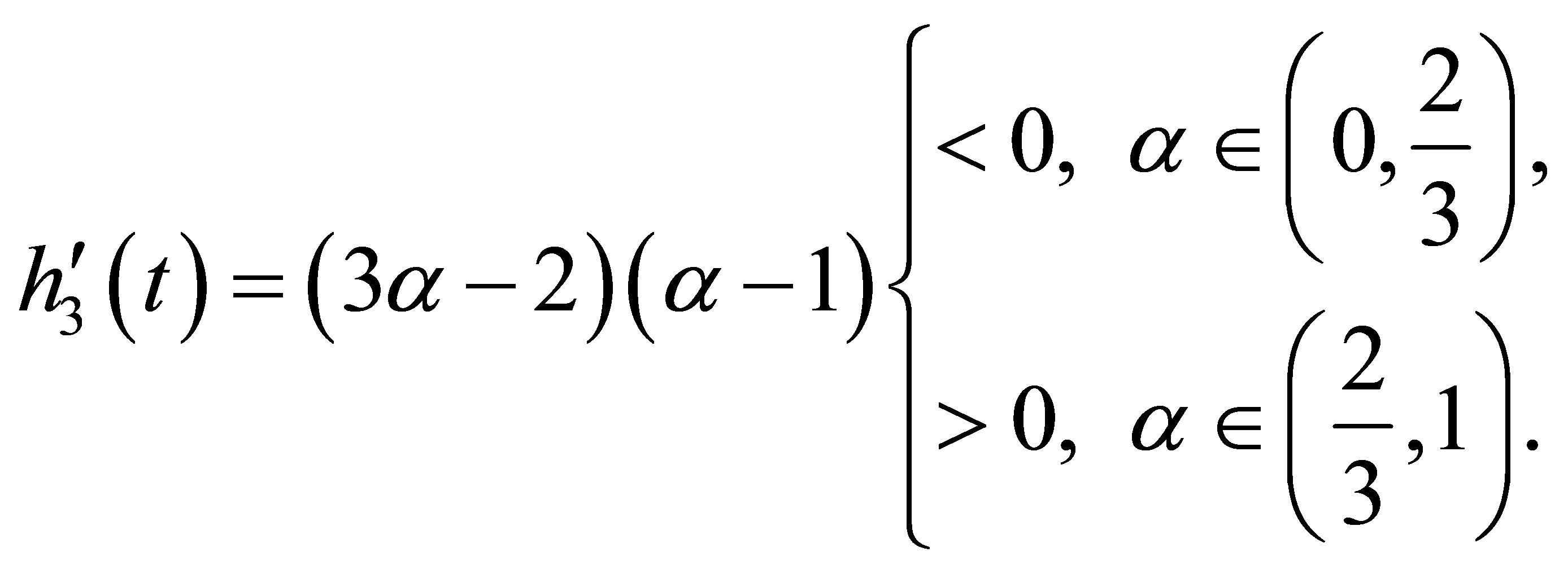
Thus  is strictly decreasing for
is strictly decreasing for 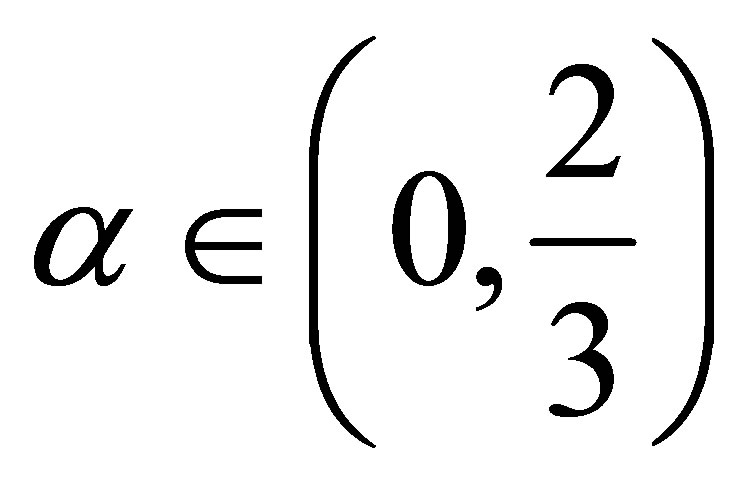 and strictly increasing for
and strictly increasing for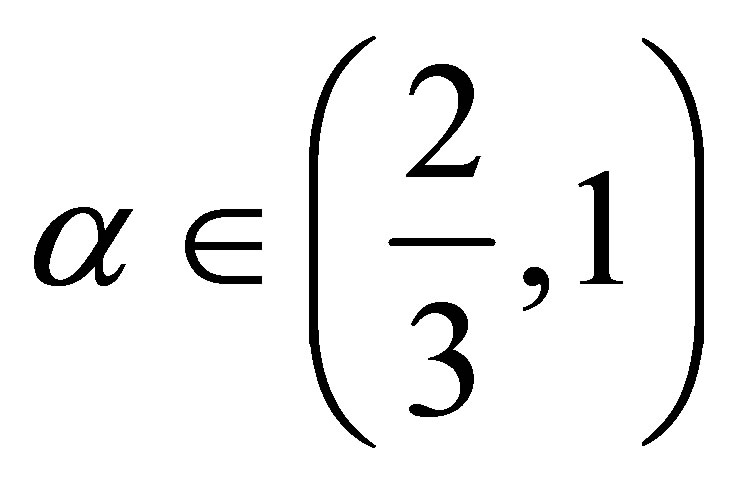 . (2.14) yields
. (2.14) yields 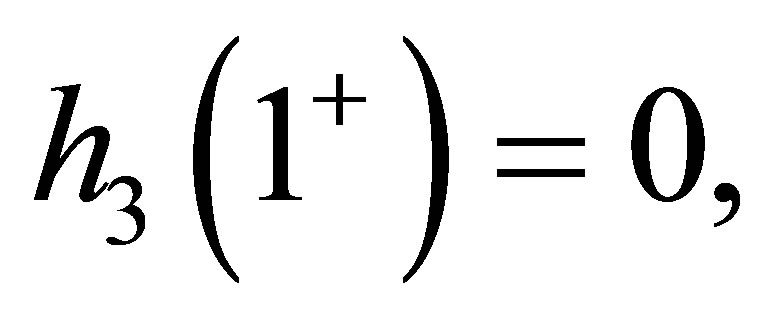 then
then 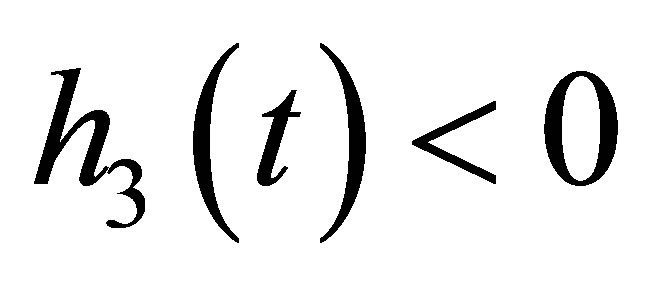 for
for 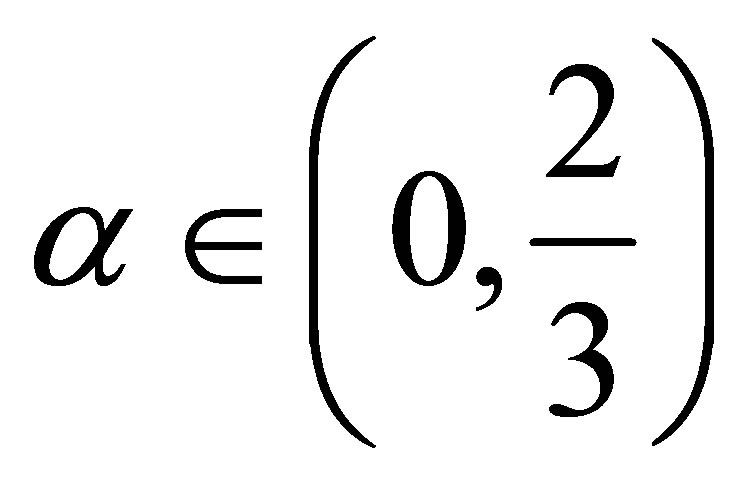 and
and  for
for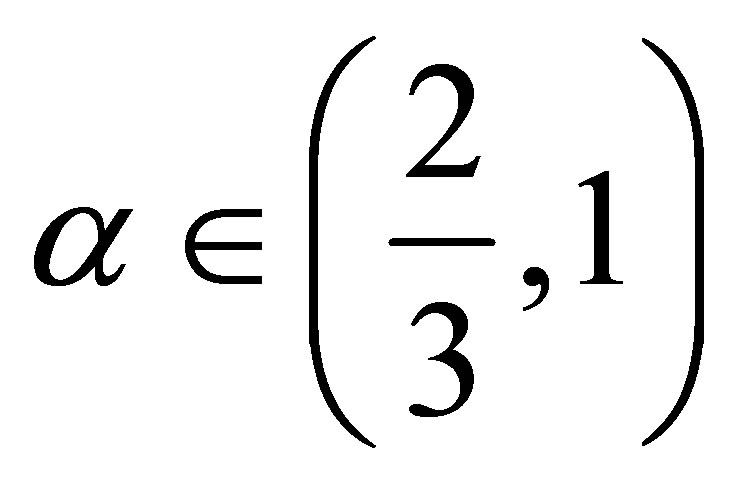 . The same reasoning applies to
. The same reasoning applies to 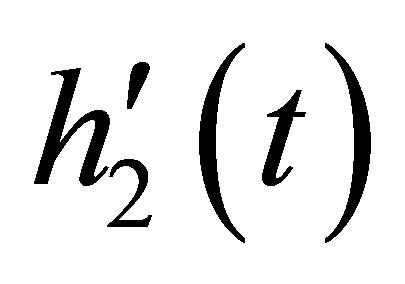 and
and 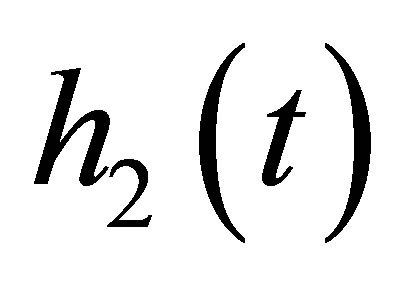 as well, and noticing (13) and (12), one has
as well, and noticing (13) and (12), one has
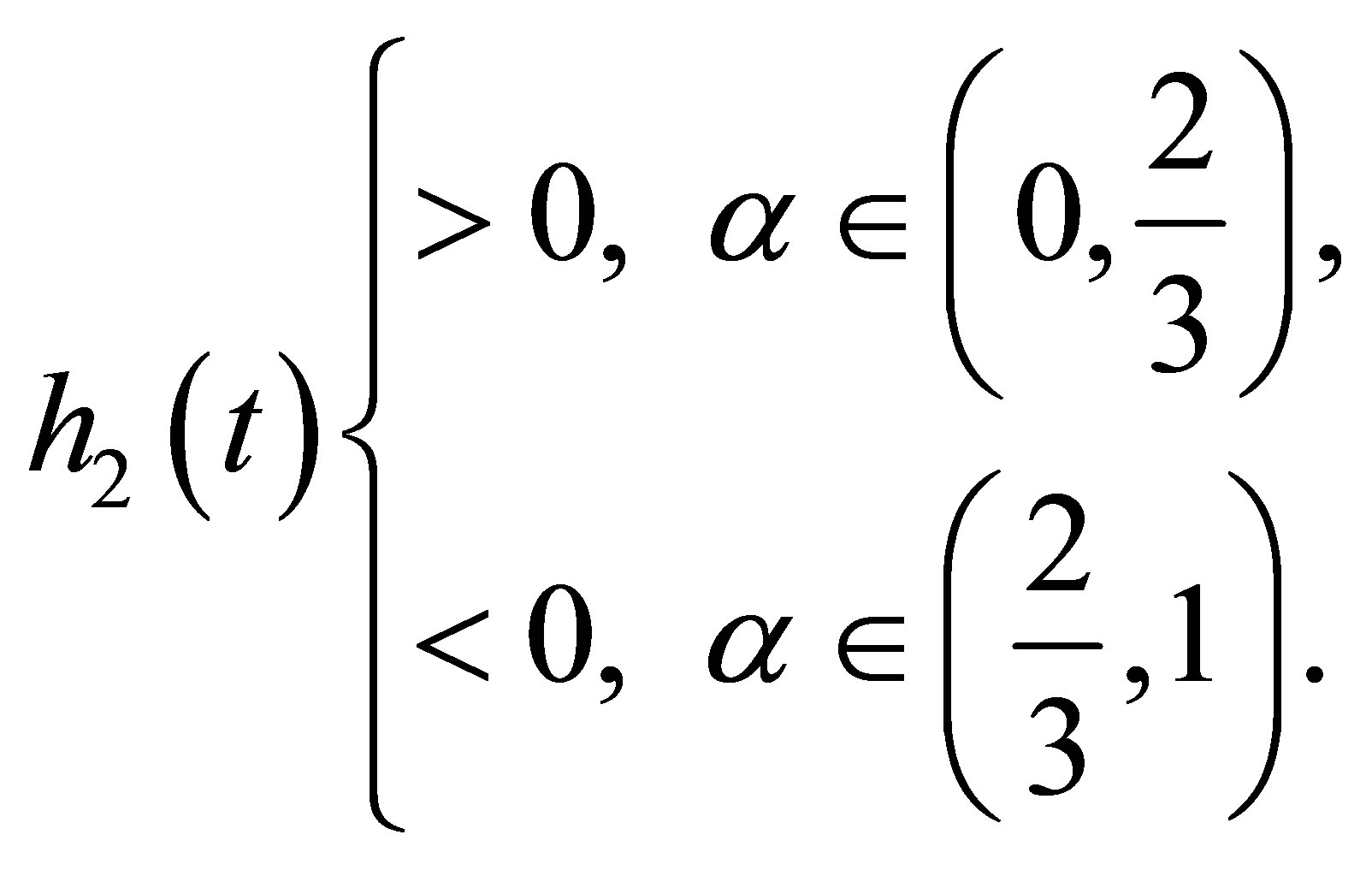
This result together with (11) implies
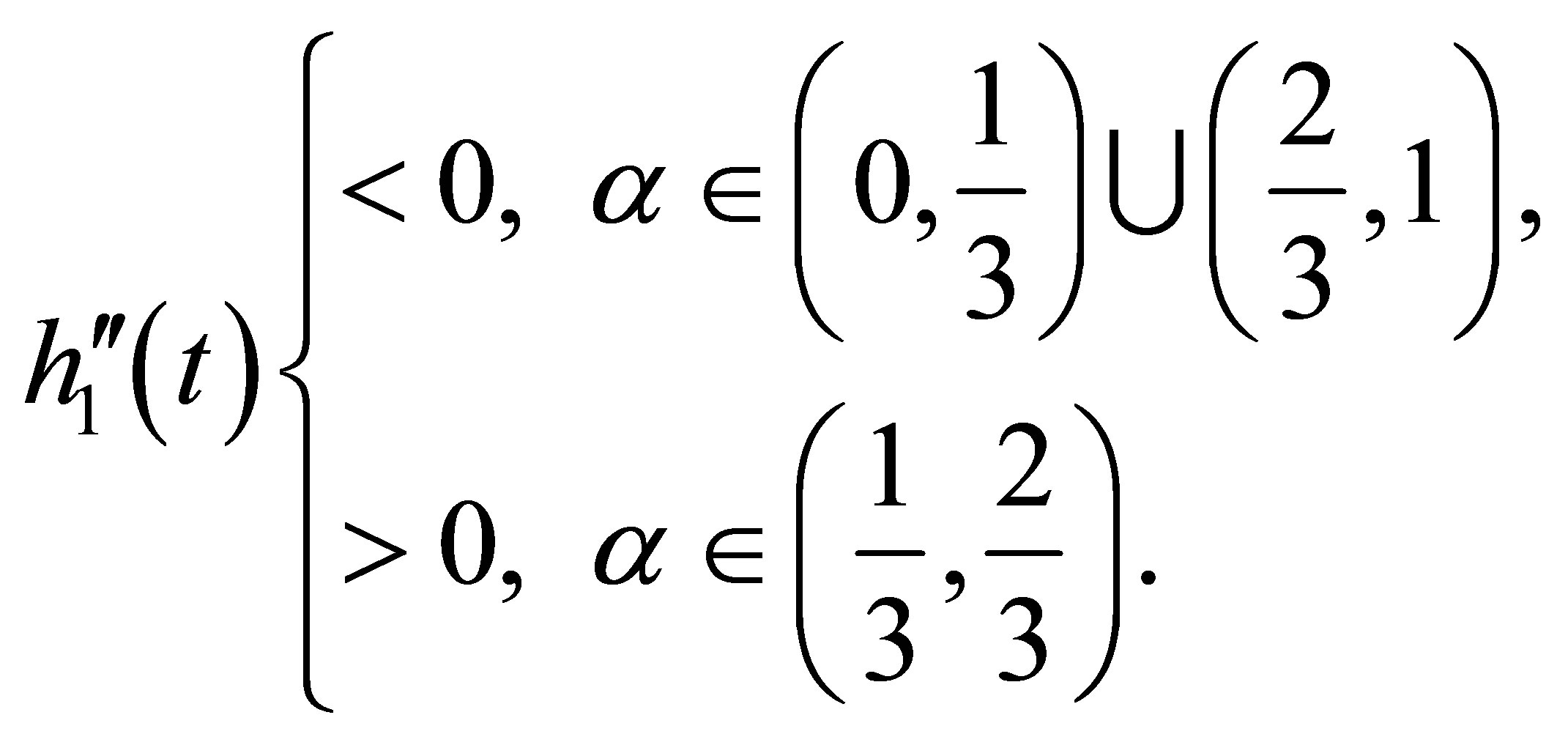
Thus  is strictly decreasing for
is strictly decreasing for
 and strictly increasing for
and strictly increasing for  The same reasoning applies to
The same reasoning applies to 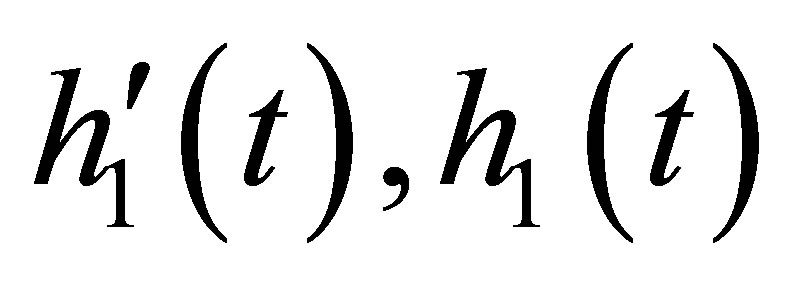
and 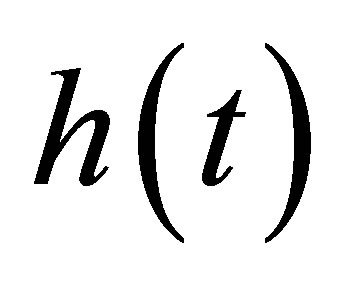 as well, and applying (8)-(10), we derive
as well, and applying (8)-(10), we derive
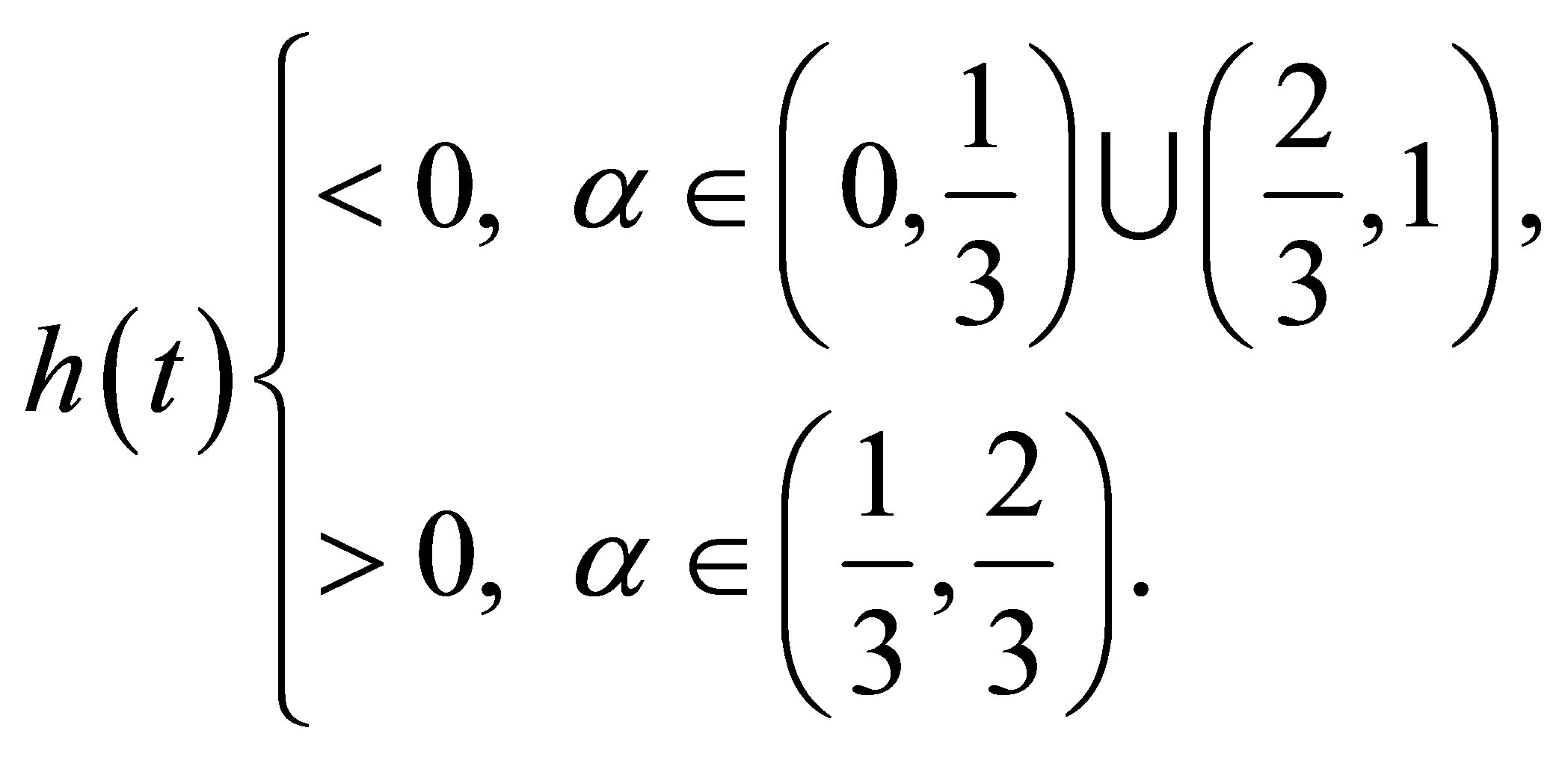
Since 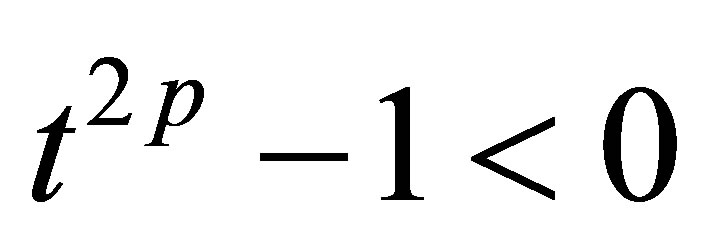 for
for 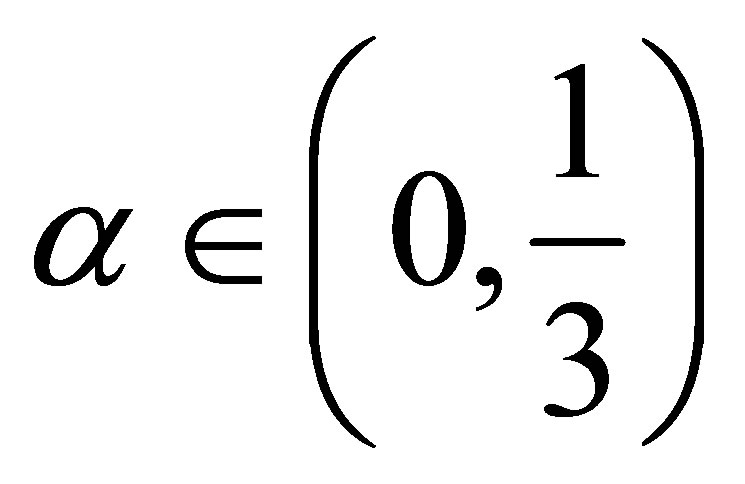 and
and 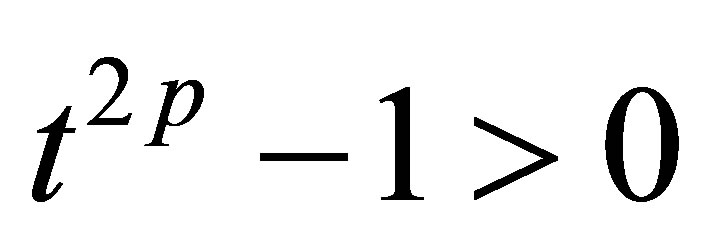 for
for , then we know from (7) that
, then we know from (7) that
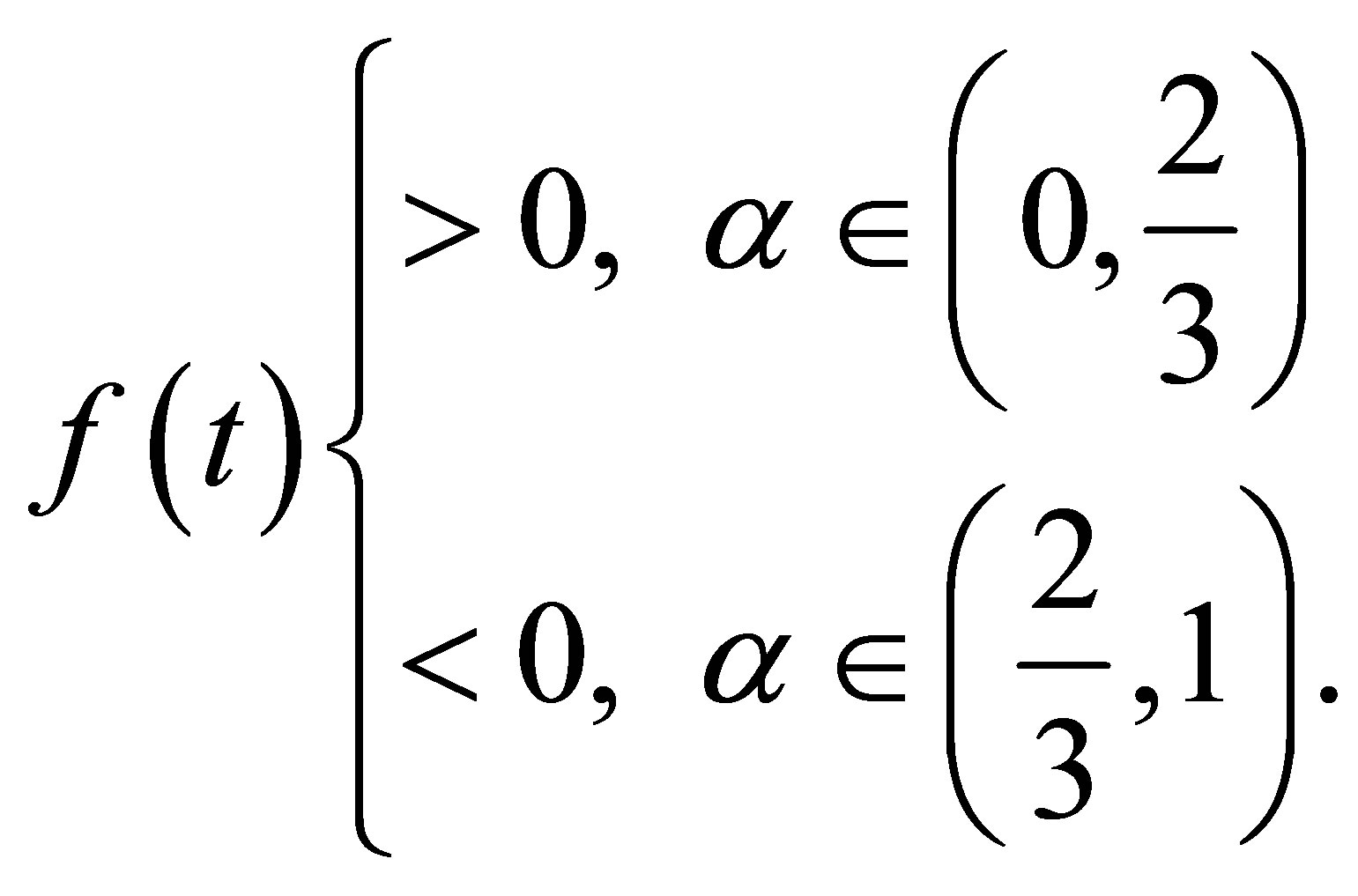
This implies the left-hand side of 2) and the right-hand side of 3).
Case 2.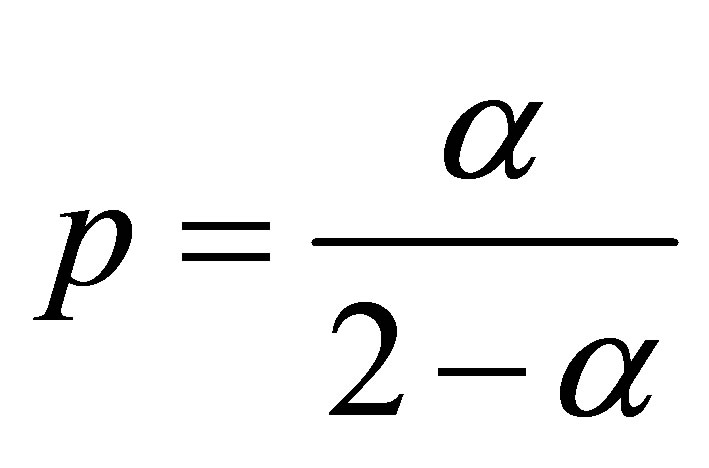 . From (14) we know that
. From (14) we know that
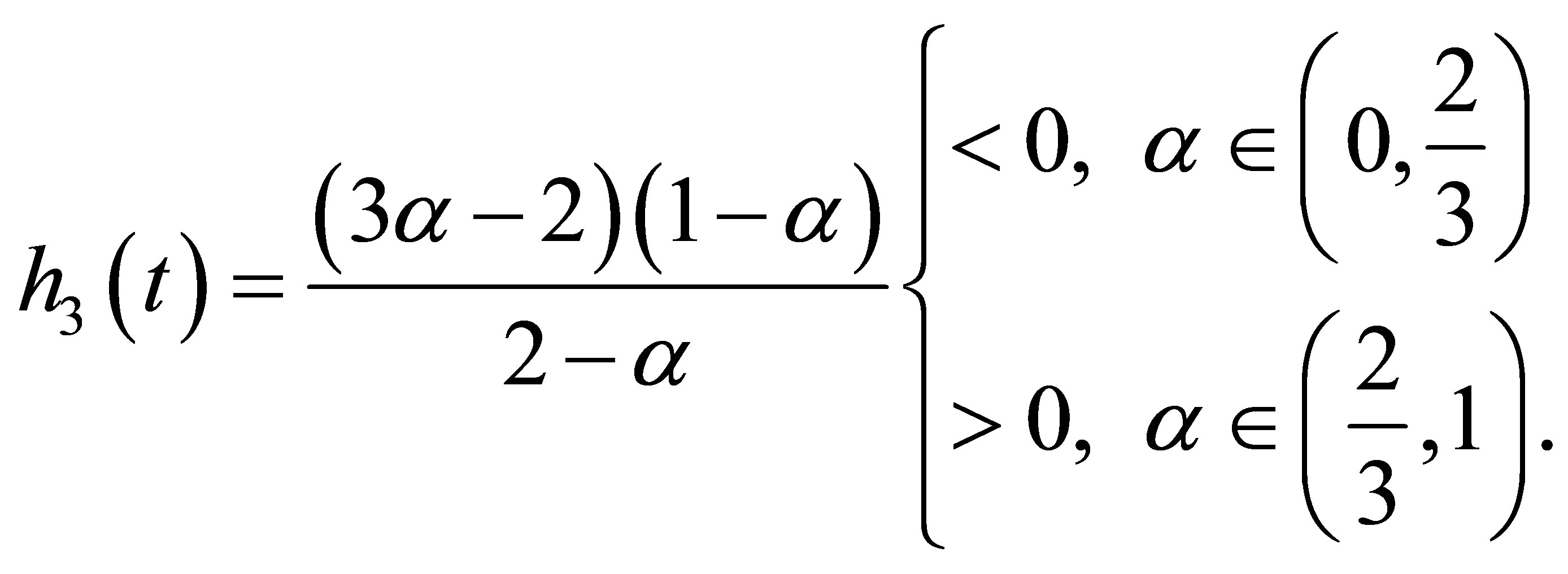
From (13) we know that 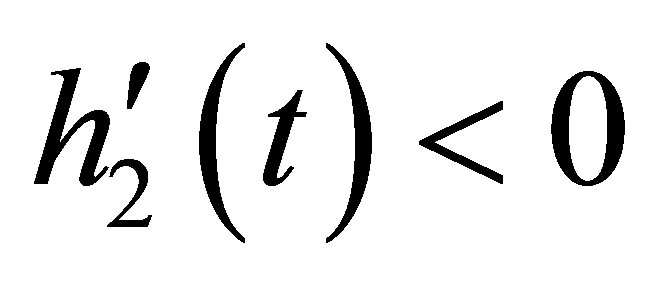 for
for 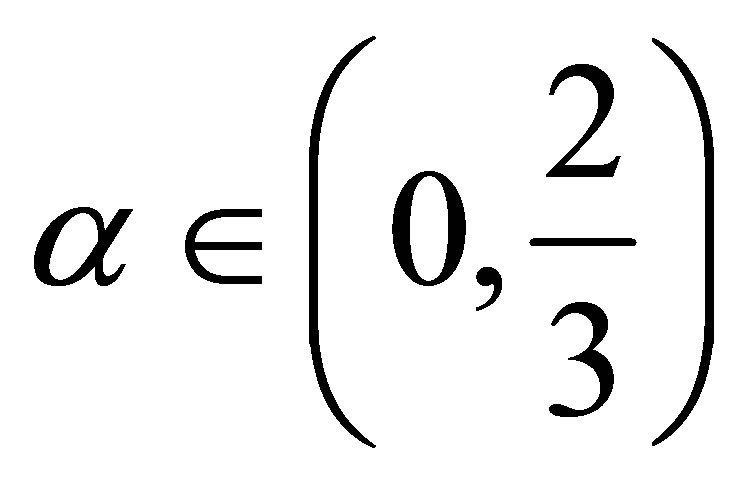 and
and 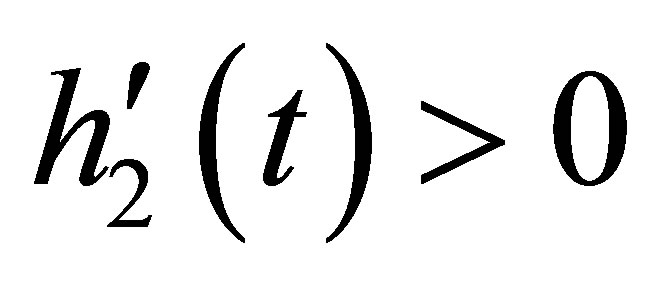 for
for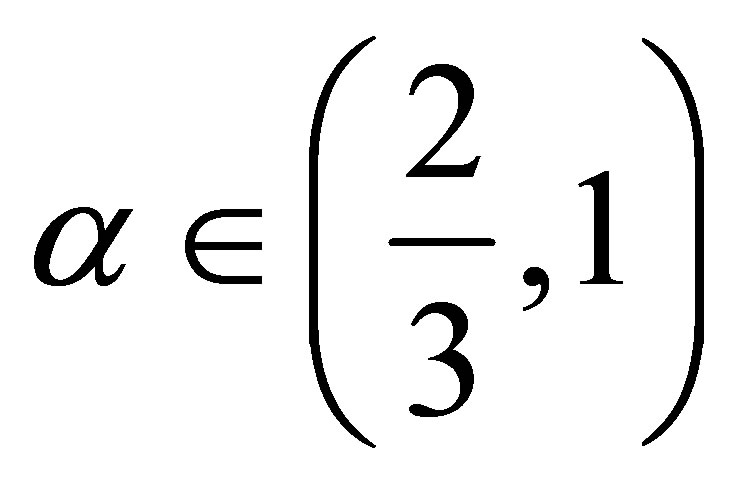 . This implies
. This implies  is strictly decreasing for
is strictly decreasing for 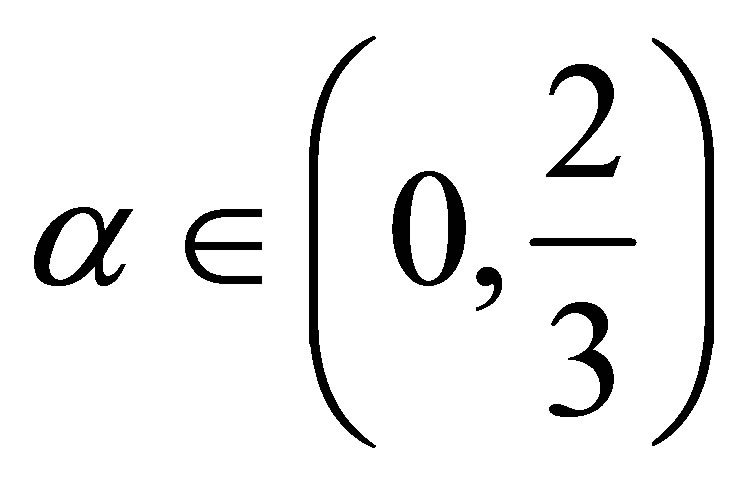 and strictly increasing for
and strictly increasing for . From (12) we know
. From (12) we know
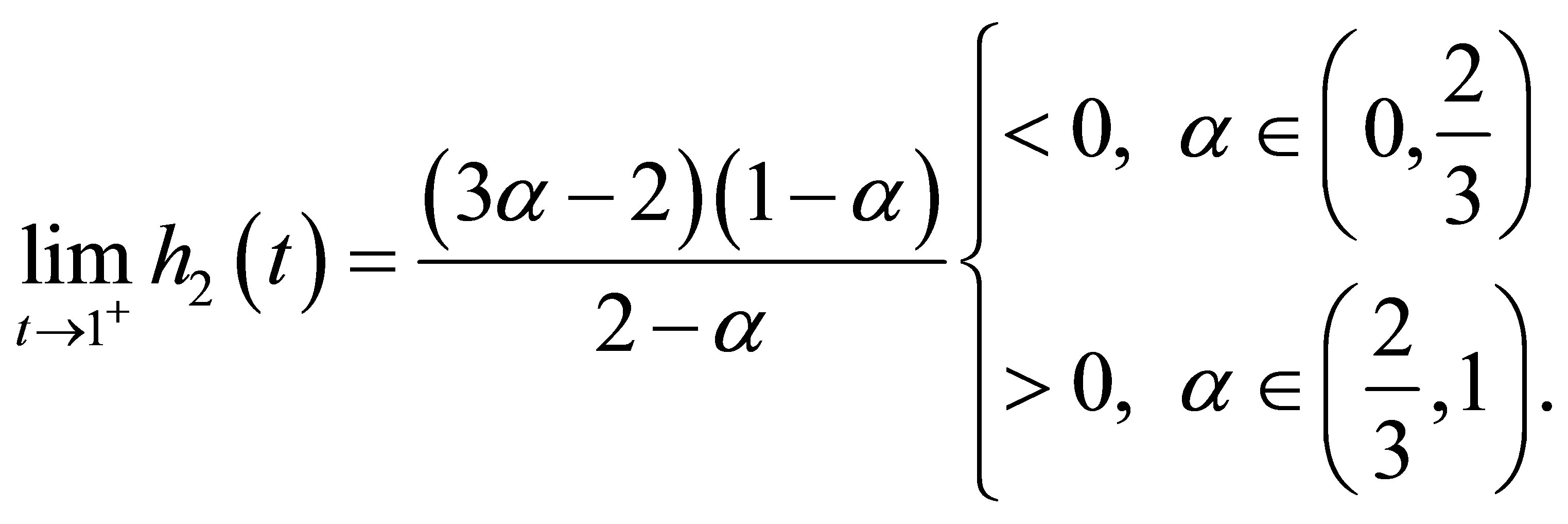
Therefore
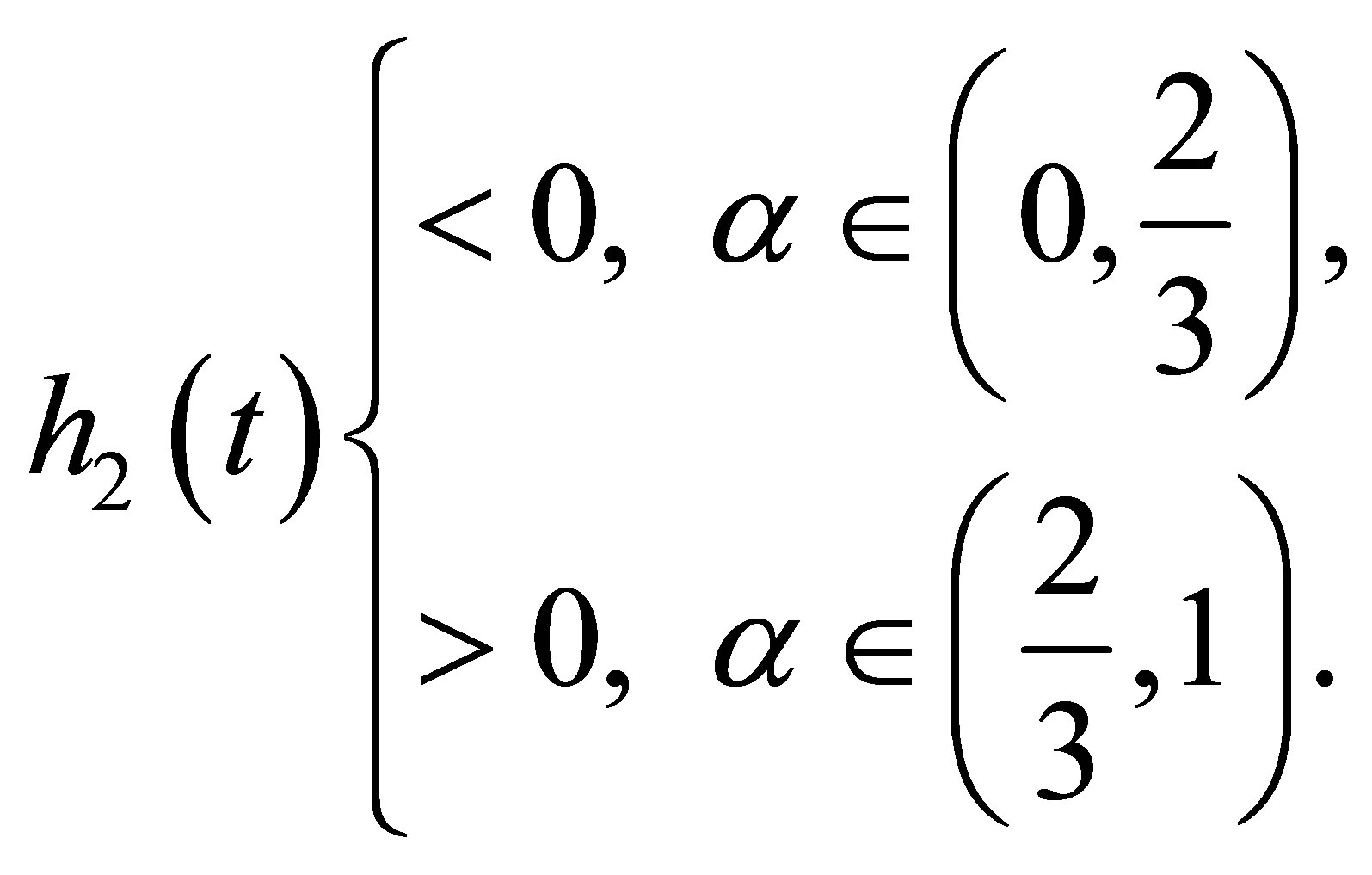
(11) implies  has the same property as
has the same property as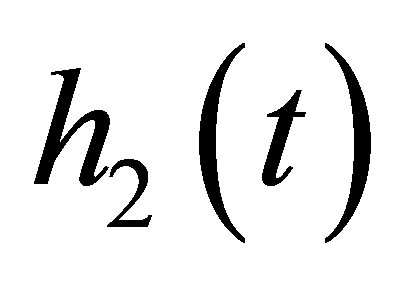 thus
thus 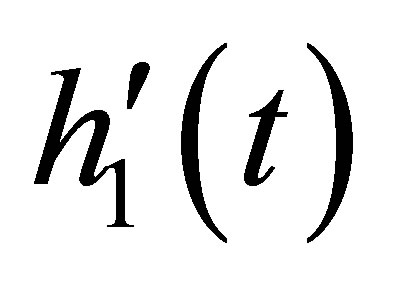 is strictly decreasing for
is strictly decreasing for  and strictly increasing for
and strictly increasing for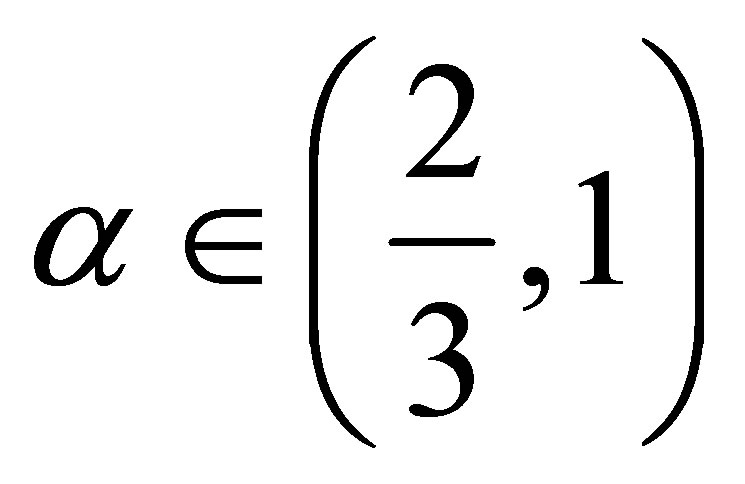 . The same reasoning applies to
. The same reasoning applies to ,
,  and
and 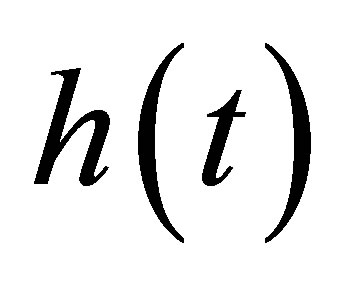 as well, and noticing (9) and (8), one has
as well, and noticing (9) and (8), one has

which together with (7) implies
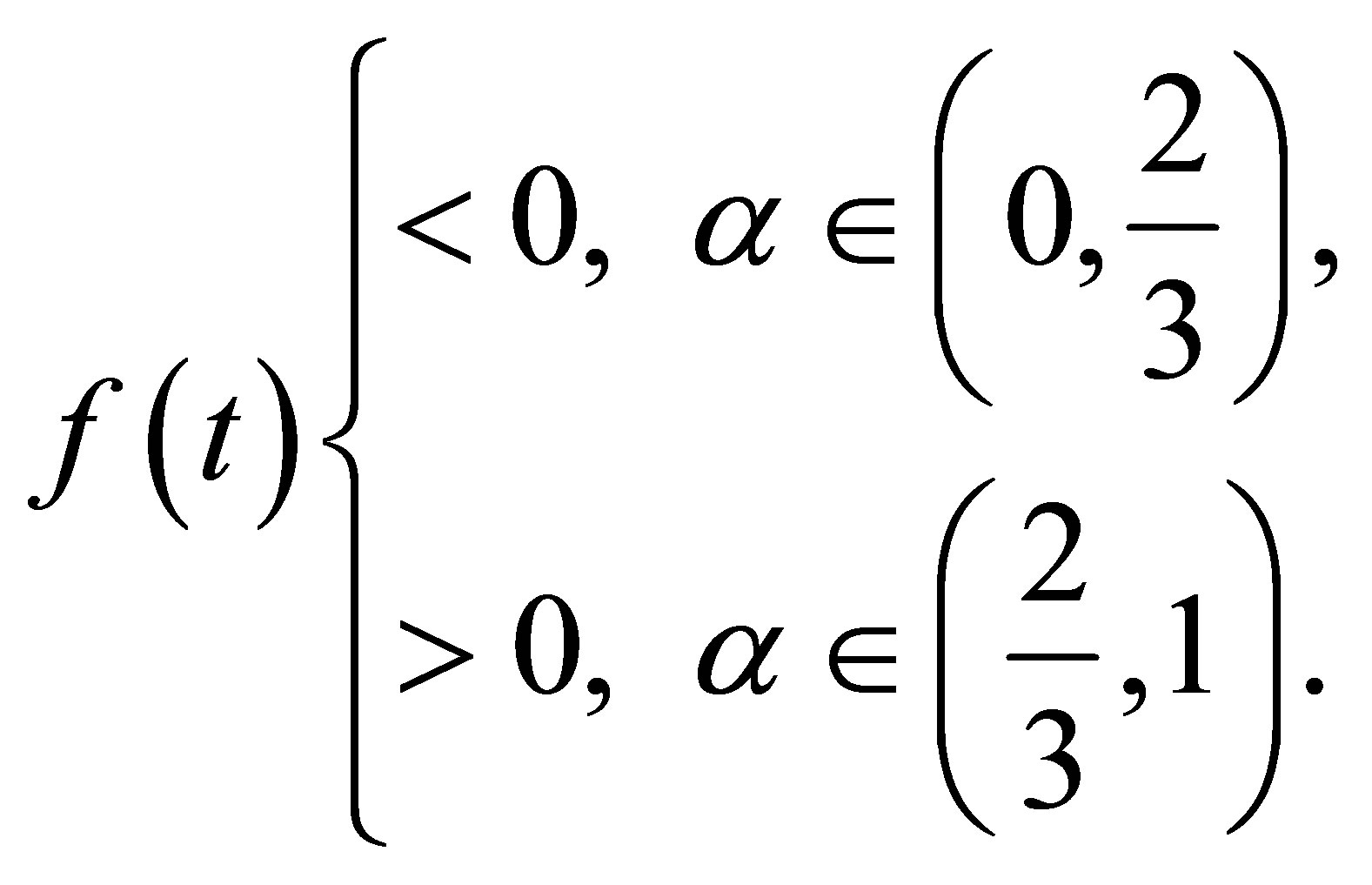
This implies the right-hand side of 2) and the left-hand side of 3).
We are now in the position to prove the constants
 and
and 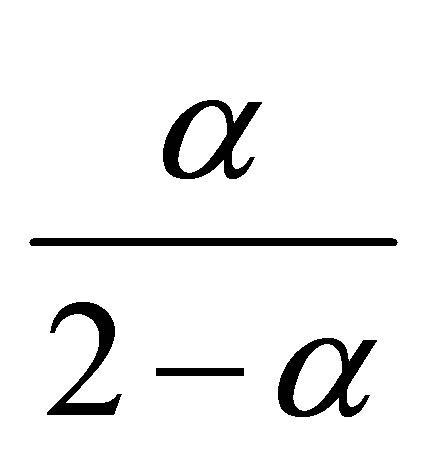 are optimal.
are optimal.
For any 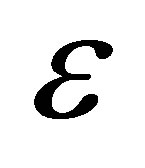 (positive or negative, with
(positive or negative, with  sufficiently small) we consider the case
sufficiently small) we consider the case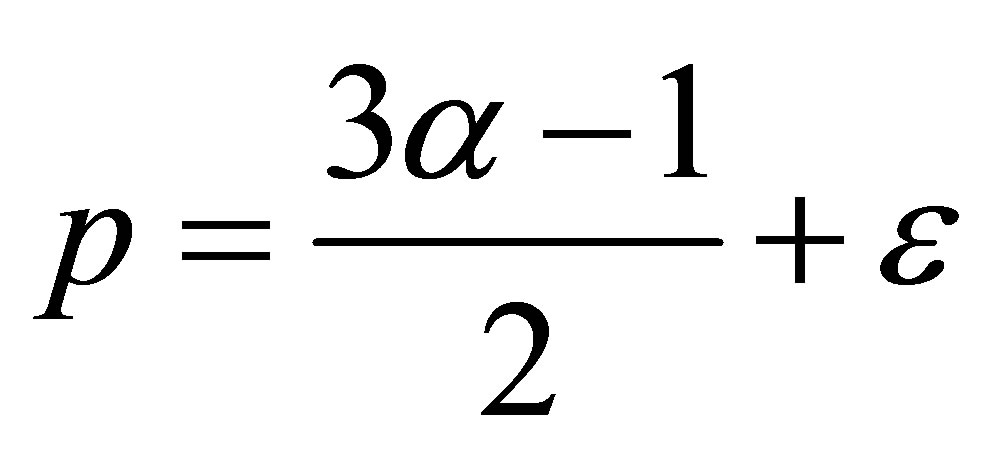 . (12)
. (12)
implies
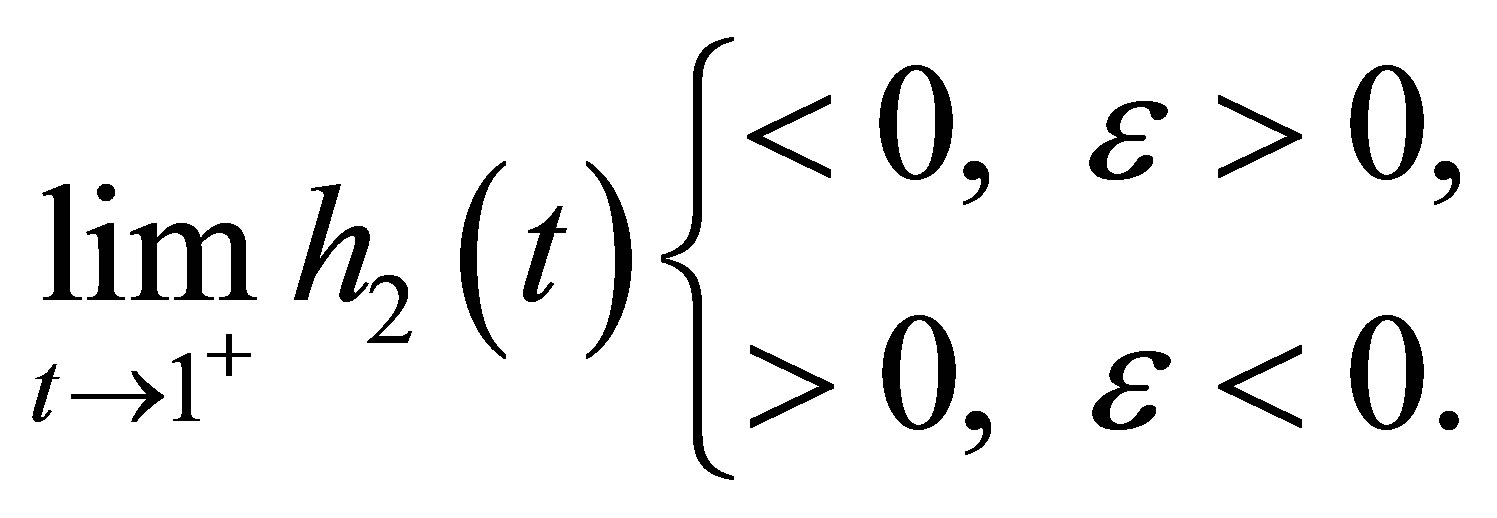
By the continuity of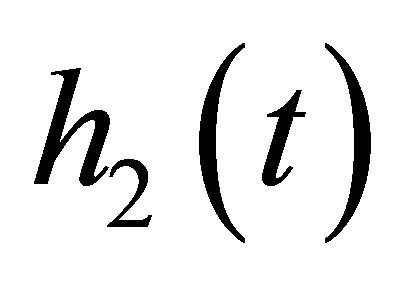 , there exists
, there exists 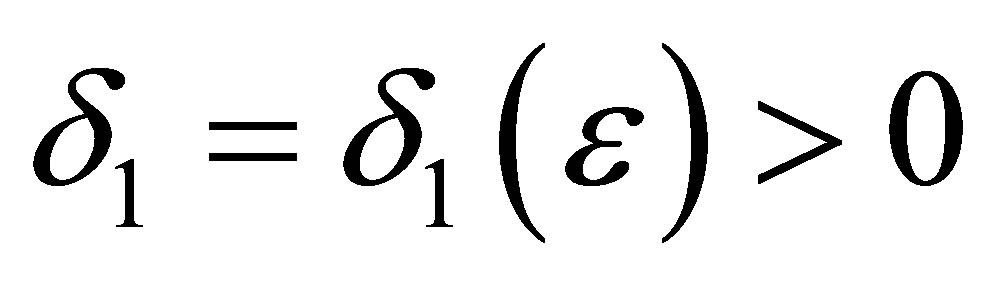 such that
such that
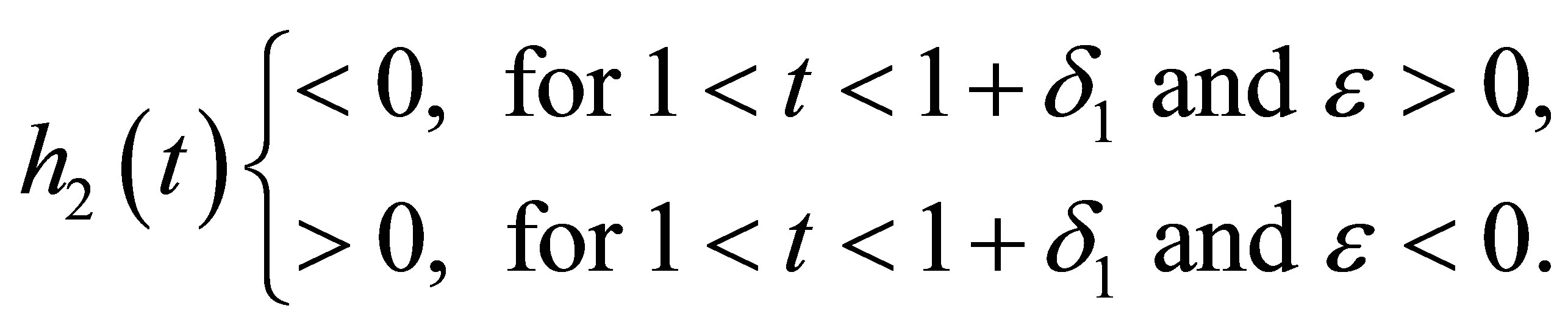
By (11), 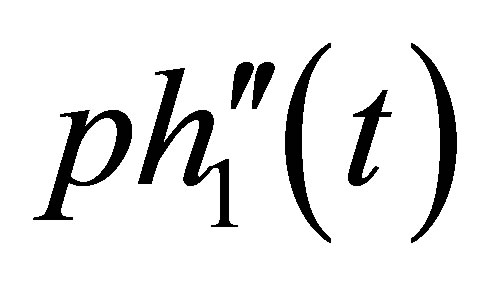 as the same property as
as the same property as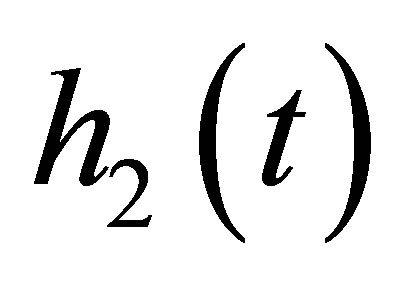 . The same reasoning applies to
. The same reasoning applies to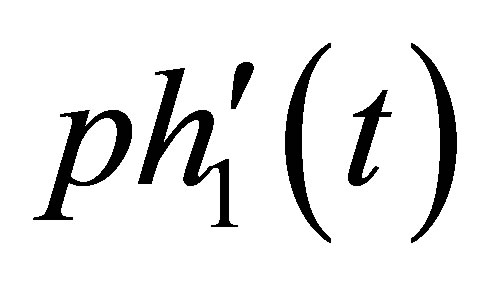 ,
, 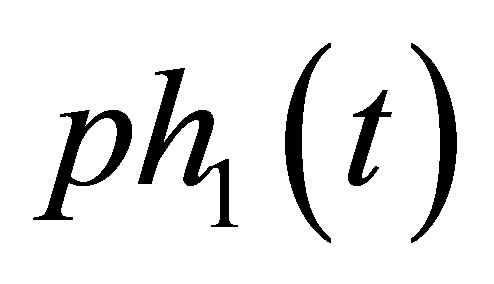 ,
, 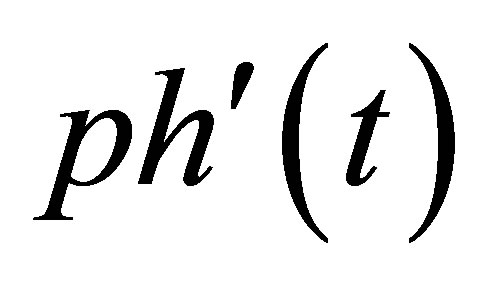 and
and 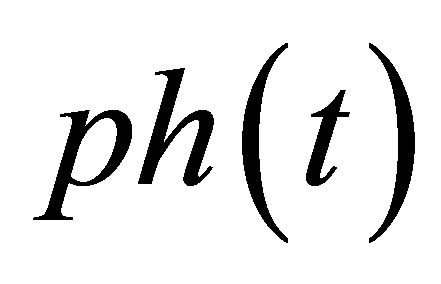 as well, and noticing (10)-(8), we know
as well, and noticing (10)-(8), we know  has the same property as
has the same property as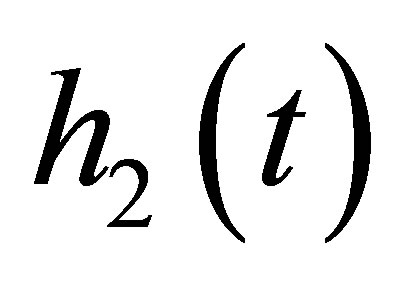 . By (7) one has
. By (7) one has
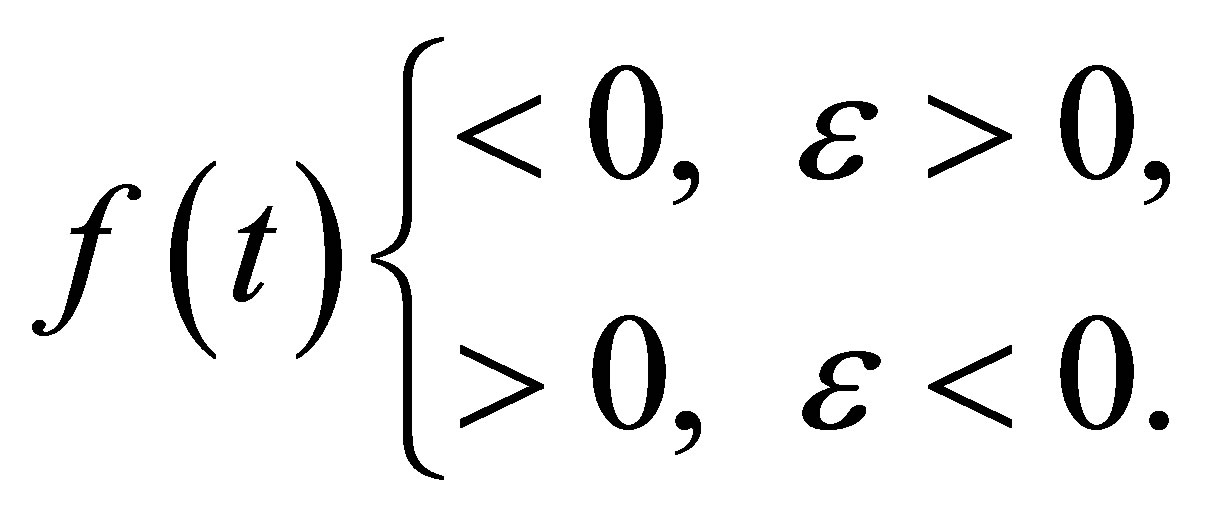
This proves the optimality for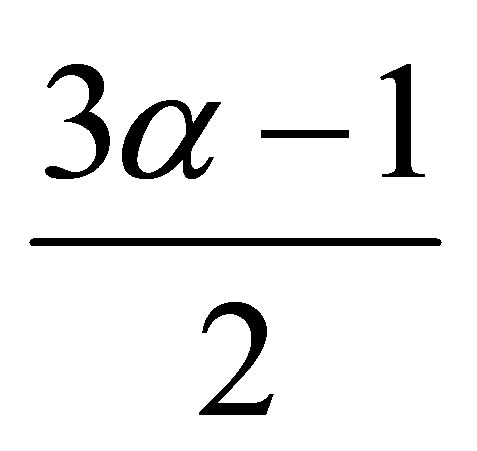 .
.
To prove the optimality for 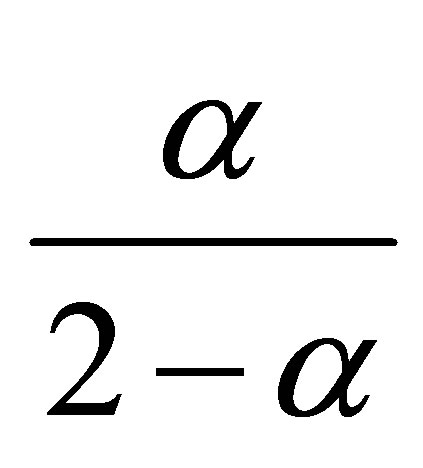 in the right-hand side of 2) and the left-hand side of 3), we notice from
in the right-hand side of 2) and the left-hand side of 3), we notice from
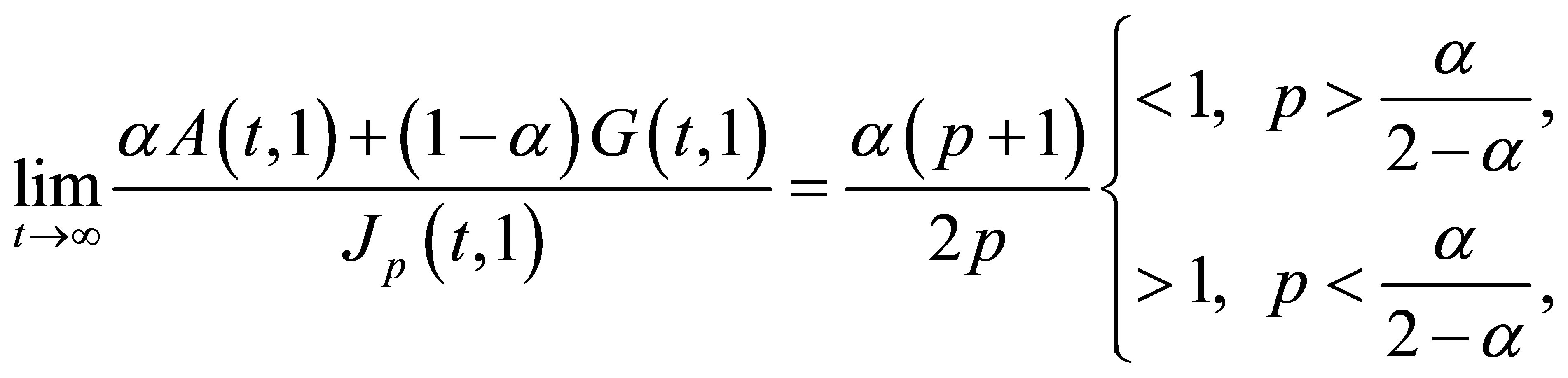
that there exists  such that
such that
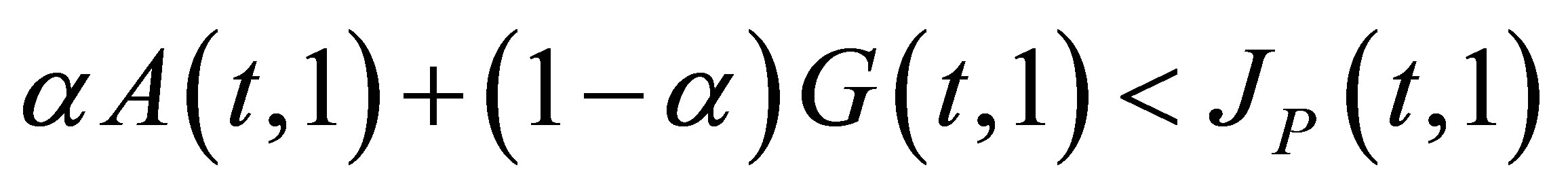
for  and
and 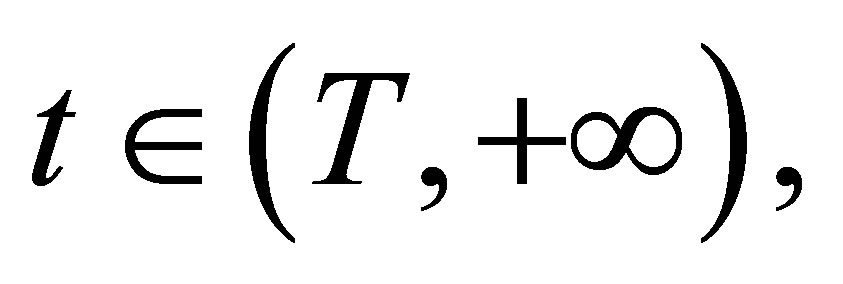 and
and
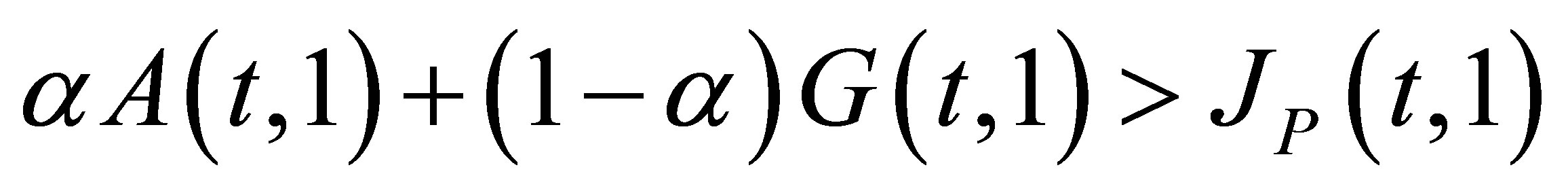
for 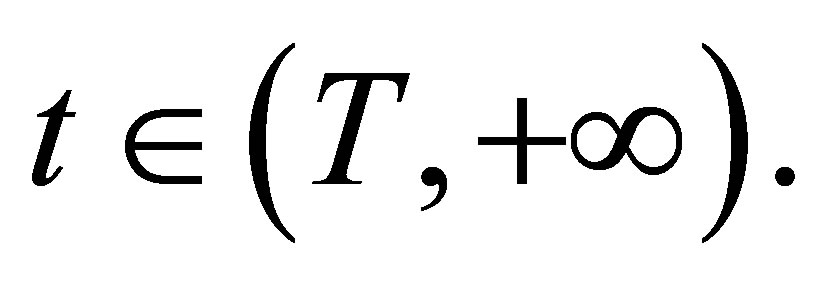 This ends the proof of Theorem 2.1.
This ends the proof of Theorem 2.1.
3. Acknowledgements
This paper is supported by NSF of Hebei Province (A2011201011).
REFERENCES
- H. Y. Gao and W. J. Niu, “Sharp Inequalities Related to One-Parameter Mean and Gini Mean,” Journal of Mathematical Inequalities, Vol. 6, No. 4, 2012, pp. 545-555.
- W. S. Cheung and F. Qi, “Logarithmic Convexity of the One-Parameter Mean Values,” Taiwanese Journal of Mathematics, Vol. 11, No. 1, 2007, pp. 231-237.
- M. K. Wang, Y. F. Qiu and Y. M. Chu, “An Optimal Double Inequality among the One-Parameter, Arithmetic and Harmonic Means,” Revue D’Analyse Numerique de Theorie de L’approximation, Vol. 39, No. 2, 2012, pp. 169-175.
- H. N. Hu, G. Y. Tu and Y. M. Chu, “Optimal Bouds for the Seiffert Mean in Terms of One-Parameter Means,” Journal of Applied Mathematics, Vol. 2012, No. 1, 2012, Article ID: 917120.
- B. Y. Long and Y. M. Chu, “Optimal Inequalities for Generalized Logarithmic, Arithmetic and Geometric Mean,” Journal of Inequalities and Applications, Vol. 2010, No. 1, 2010, Article ID: 806825.
- N. G. Zheng, Z. H. Zhang and X. M. Zhang, Schur-Convexity of Two Types of One-Parameter Mean Values in Variables,” Journal of Inequalities and Applications, Vol. 2007, No. 1, 2007, Article ID: 78175.

