ABSTRACT

A topological index is a numerical value associated with chemical constitution for correlation of chemical structure with various physical properties, chemical reactivity or biological activity. In this paper, we computed the Omega and Cluj-Ilumenau indices of a very famous hydrocarbon named as Polycyclic Aromatic Hydrocarbons for all integer number k.

Keywords:

Molecular Graph, Hydrocarbons, Topological Indices

1. Introduction

Let 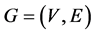be a simple finite connected graph, where V and E are the sets of vertices and edges, respectively. The distance between two vertices u and v in a graph G is the length of the shortest path connecting them, it is denoted by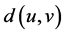. Two edges 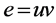and 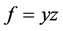in graph G are said to be codistant if they satisfy the following condition [1]

.

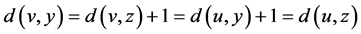If the edges e and f are codistant we write it as e co f. Relation co is reflexive and symmetric but generally not transitive. If co relation is transitive then it is an equiva- lence relation. A graph G in which co is an equivalence relation is called co-graph, and the subset of edges 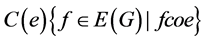is called an orthogonal cut (oc) of G, also the edge set 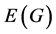can be written as the union of disjoint orthogonal cuts, i.e.

.

Let 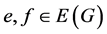be two edges of G which are opposite or topologically parallel and denote this relation by e op f. A set of opposite edges, within the same ring eventually forming a strip of adjacent rings, is called an opposite edge strip ops, which is a quasi orthogonal cut (qoc). The length of ops is maximal irrespective of the starting edge. Let 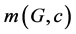be the number of ops strips of length c.

The physico-chemical properties of chemical compounds are often modeled by means of molecular graph based structure descriptors, known as topological indices [2] , [3] . The Wiener index is the first distance based topological index [4] . The Wiener index of a graph G is defined as

.

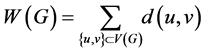M. V. Diudea introduced the Omega Polynomial 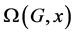for counting ops strips in graph G [5]

.

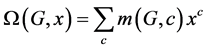First derivative of Omega polynomial at 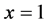equals the size of the graph G, i.e.

.

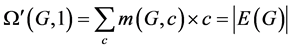The Cluj-Ilumenau index [6] is defined with the help of first and second derivative of Omega polynomial at 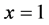as

.

The Omega index is defined as

.

2. Discussion and Main Result

Polycylic Aromatic Hydorcarbons () are a group of more than 100 different chemicals, these are formed during the incomplete burning of coal, oil, gas, garbage or other substances. are usually found as a mixture containing two or more of these compounds. For further information and results on and other molecular graphs and nano-structures, we refer [7] - [22] . In this section, we computed the Omega and Cluj-Ilumenau index of Polycyclic aromatic hydrocarbons.

Theorem 1. Consider the graph of Polycyclic aromatic hydrocarbons, then we have the following

.

Proof Consider the general representation of the Polycyclic aromatic hydrocarbons as shown in Figure 1. The structure of contain atoms/vertices and bonds/edges.

To obtain the required result, we used the Cut Method [23] - [25] . We calculated the for all opposite edge strips. From Figure 2, it is clear that there are distinct cases of qoc strips for and the graph of Polycyclic aromatic hydro- cabons’s graph is a co-graph. The size of a qoc strip is for

and. Because there are co-distant edges with

. Also from Figure 2 one can notice that the number of repetition of these qoc stips is six and the number of repetition of is three times. i.e.

・ For, and

・ For all, and

・ For, and

From this, we obtain that

.

This gives that the Omega polynomial of the Polycyclic aromatic hydrocarbons for all non-negative integer number t is equal to

.

Now with the help of above polynomial we will investigate the Cluj-Ilmenau and Omega indices of Polycyclic aromatic hydrocarbons.

As

Cite this paper

Kanna, M.R.R., Kumar, R.P., Jamil, M.K. and Farahani, M.R. (2016) Omega and Cluj-Ilmenau Indices of Hydrocarbon Molecules “Polycyclic Aromatic Hydrocarbons PAH_k”. Computational Chemistry, 4, 91-96. http://dx.doi.org/10.4236/cc.2016.44009

References