Received 15 September 2015; accepted 25 October 2015; published 28 October 2015

ABSTRACT

Ground state geometries, spectral (IR and UV-Vis) properties, analysis of frontier molecular orbitals (FMOs), natural bond orbital (NBO) analysis and molecular electrostatic potential (MEP) surfaces of three transition metal complexes [Cu(AOYP)₂(OH₂)₂] (A), [Ni(AOYP)₂(OH₂)₂] (B) and [Zn- (AOYP)₂(OH₂)₂] (C), have been studied theoretically by the Density Functional Theory (DFT) and Time-Dependent Density Functional Theory (TD-DFT) methods. AOYP is the oxadiazole ligand 2-(5-amino-[1,3,4]-oxadiazol-2-yl)phenol. The geometries of these complexes were initially optimized using two basis sets: LAN2DZ and a generic basis set, the latter of which was selected for subsequent analysis. The stability of the complexes arising from intramolecular interactions and electron delocalization was estimated by natural bond orbital (NBO) analysis. The NBO results showed significant charge transfer from lone pair orbitals on the AOYP donor atoms O19, O21, N15 and N36 to central metal ions in the complexes, as well as to the benzene and oxadiazole rings. The electronic spectrum of (A) showed bands at 752 and 550 nm mainly attributable to ligand-to- metal charge transfer (LMCT) transitions, and a band at 446 nm assigned to a d-d transition. The electronic spectrum of (B) consisted of bands at 540, 463 and 395 nm mainly due to d-d transitions. Calculated electronic bands for (C) occurred at 243, 238 and 235 nm, arising from intra- ligand charge transfer (ILCT) transitions within AOYP. A good agreement in terms of band positions was found between experimental and calculated absorption spectra of the complexes.

Keywords:

DFT, TD-DFT, AOYP Complexes, NBO Analysis, MEP Surfaces

1. Introduction

Oxadiazoles constitute a very important class of ligands in coordination chemistry due to their wide applications in the synthesis of a large variety of transition metal complexes with diverse biological activities such as anti-inflammatory, antifungal, antibacterial, antiviral, anti-HIV and anticancer activities [1] -[4] . Transition metal complexes with oxadiazoles show enhanced antimicrobial activity compared to free oxadiazole ligands, probably due to the greater lipophilic nature of the complexes that favors their permeation through the lipid layers of the bacterial cell membranes [5] [6] . Researchers have been focusing more attention on transition metal complexes with 1,3,4-oxadiazoles and their derivatives in an effort to design and develop new therapeutic agents with novel chemical structures, with an inclination towards different modes of action rather than simply creating analogs of the existing ones [7] .

In the search for novel antimicrobial agents based on a backbone of oxadiazoles, researchers have in the recent years synthesized, characterized and studied the antimicrobial properties of a variety of complexes with 1,3,4-oxdiazole ligands. In 2013, Wanale and co-workers synthesized and characterized complexes of 2-(5- amino-[1,3,4]-oxadiazol-2-yl)phenol with Cu(II), VO(IV), Ni(II), Zn(II) and Cd(II), but did not determine their geometrical parameters (bond lengths, bond angles and dihedral angles). These parameters can be conveniently determined theoretically, by quantum chemical calculations. To the best of our knowledge, a theoretical study of the geometries and properties of these complexes has not been reported in the literature. This inadequacy encouraged us to pursue theoretical studies on the work of Wanale and co-workers in order to determine stable geometries and shapes of [Cu(AOYP)₂(OH₂)₂] (A), [Ni(AOYP)₂(OH₂)₂] (B) and [Zn(AOYP)₂(OH₂)₂] (C) as well as various microscopic properties. Shape is a fundamentally important molecular feature that often determines drug activity [8] . A rigorous control of molecular geometry and shape is crucial to the drug design process because different geometric, steric and conformational properties of a biologically active molecule can give rise to different potencies, types of activity and unwanted effects [9] .

The purpose of the present study was to theoretically optimize the geometries of (A)-(C) and then determine their spectral (IR and UV-Vis) properties, charge delocalization patterns from NBO analysis, frontier molecular orbital compositions and MEP surfaces, via Density Functional Theory (DFT) and Time-Dependent Density Functional Theory (TD-DFT) calculations. The DFT method was chosen for this study because it is faster, less computationally intensive, takes electron correlation into account and has a precise accuracy in reproducing experimental data [10] . In addition, DFT was developed especially for calculations on complexes [11] and has been proven to be a very reliable method for complexes of transition metals [12] . DFT is generally considered to be a good compromise between accuracy and computational time.

2. Computational Details

Theoretical calculations on (A)-(C) were carried out using Gaussian 09 rev. A.02 [13] . The input files to Gaussian 09 were prepared with Gauss View 5.0.8 [14] . We chose Becke’s three-parameter Lee-Yang-Parr hybrid functional (B3LYP) [15] to carry out all calculations. The geometries of the complexes were optimized in gas and solution phases at two levels of theory (B3LYP/LANL2DZ and B3LYP/GEN), for comparison. At the B3LYP/LANL2DZ level, the LANL2DZ basis set was used on all atoms whereas at the B3LYP/GEN level, transition metal ions were still represented with the LANL2DZ basis set while all other atoms used the 6-31G(d) basis set. After comparing results, we settled on the B3LYP/GEN level for the rest of the calculations. The 6-31G(d) basis set is a popular polarized Pople basis set which adds d functions to C, N and O atoms, whereas LANL2DZ is a basis set for post-third-row atoms which uses effective core potentials to reduce computational cost [16] . The use of a relativistic effective core potential (ECP) on Cu, Ni and Zn replaces the inner core electrons [17] . Solvent effects were investigated using the Polarizable Continuum Model (PCM) of solvation by the Integral Equation Formalism (IEF) approach [18] . Dimethyl sulphoxide (DMSO) and water were used as solvents. DMSO was chosen as a solvent because the complexes were originally synthesized and characterized in it while water was chosen for comparison because the vast majority of biological processes in living organisms occur in water. Electronic excitation energies and wavelengths of the complexes were calculated using the TD-DFT/B3LYP method. NBO calculations were performed on the complexes using the NBO 3.1 [19] module embedded in Gaussian 09, still using density functional theory.

3. Results and Discussion

3.1. Selection of Basis Set

Careful selection of basis sets is very important for accurate prediction of the properties of transition metal complexes. To select an appropriate basis set for the current study, we optimized the geometries of (A)-(C) using LANL2DZ and a generic basis sets. The optimized molecular structures of (A), (B) and (C) in the gas phase, are shown in Figures 1-3 respectively. In Figure 1, (A1) and (A2) are used to distinguish between molecular structures optimized at the B3LYP/GEN and B3LYP/LANL2DZ levels of theory respectively. (B1) and (B2) in Figure 2 and (C1) and (C2) in Figure 3, represent similar comparisons for structures (B) and (C). The geometry of (A) was optimized using the unrestricted open-shell model (UB3LYP) while those of (B) and (C) were optimized using the restricted closed-shell model (RB3LYP). No constrains on symmetry, bonds, angles or dihedral angles were applied in the geometry optimization calculations. The absence of imaginary frequencies confirmed that the stationary points obtained after geometry optimization corresponded to minima on the potential energy hyper surfaces [20] . Selected structural parameters of these complexes are listed in Table 1. The metal-ligand (M-L) bond lengths calculated with the generic basis set are very similar to those calculated with LANL2DZ basis set, except the case of M-O bond lengths involving the H₂O ligands, where significant discrepancies are

^aM represents the central metal ion which is Cu(II) for (A), Ni(II) for (B) and Zn(II) for (C). For atomic numbering of (A), (B) and (C), refer to Figures 1-3 respectively.

observed. The values of bond angles and dihedral angles around the central metal ions calculated using the generic basis set are considered more acceptable because they are much closer to standard values in regular octahedral complexes (bond angles around the central metal in ideal octahedral complexes are 90˚ each). From the values of geometrical parameters around the central metal ions, the generic basis set was found to be more appropriate than the LANL2DZ basis set for calculations on the complexes and was then chosen for all calculations reported in this paper.

When the octahedral input geometry of (B) was fully optimized at both levels of theory, the output geometry was found to be square planar with the two H₂O ligands originally coordinated to the central Ni(II) ion, now linked to the NH₂ groups of the AOYP ligands through hydrogen bonds as shown in Figure 2. The square planar structures of (B1) and (B2) are confirmed by the dihedral angles O40-Ni20-O19-N36 (176.55˚ with LANL2DZ; 174.72˚ with the Generic basis set) and O43-Ni20-N15-O21 (175.30˚ with LANL2DZ; 179.18˚ with the Generic basis set), which show that the two oxygen atoms in the H₂O ligands (O40 and O43) are roughly in the same plane that contains the AOYP ligands and the central Ni(II) ion. Also, the nickel-oxygen distances Ni20-O40 and Ni20-O43 calculated at both levels of theory are around 5.1 Å which is unreasonable for a metal oxygen bond; therefore, the H₂O molecules are not coordinated to the central Ni(II) ion. The two H₂O ligands are lattice held and, hence, constitute water of crystallization. The square planar structure of the Ni(II) complex is expected because the Ni(II) ion has a d⁸ electronic structure and transition metal ions or atoms with this structure form stable square planar complexes with dsp² hybridization.

Cu(II) and Zn(II) complexes optimized with the generic basis set, (A1) and (C1) respectively have distorted octahedral geometries around the central metal ions, while the same complexes optimized with LANL2DZ basis set, (A2) and (C2) respectively, have distorted square pyramidal geometries around the central metal ions as shown in Figures 1-3. In both cases, the water molecules in the complexes are involved in hydrogen bonding. (A1) is Jahn-Teller distorted because the bonds to the central Cu(II) ion along the z-axis (O40-M20 and O43-M20 with bond lengths 3.08 Å and 2.63 Å respectively) are much longer than the bonds along the x-axis and y-axis: 2.02 Å for M20-N15 and M20-N36 and 1.96 Å for M20-O19 and M20-O21. This corresponds to an extension along the z-axis and compression along the x- and y-axes.

3.2. Vibrational Analysis

Some calculated IR gas phase frequencies and their probable assignments for AOYP and its transition metal complexes are listed in Table 2. The assignments of the calculated wavenumbers were aided by the animation option of Gauss View 5.0.8, which gives a visual presentation of the vibrational modes. The IR frequencies of AOYP were calculated at the B3LYP/6-31G(d) level of theory while those of its complexes were calculated at B3LYP/GEN level. The corresponding experimental frequencies (also listed in Table 2) were obtained from [3] and [5] . The calculated frequencies are slightly higher than the observed values for the majority of the normal

^a represents symmetric stretching vibrations of N-H and O-H bonds in the NH₂ group and H₂O ligand respectively, Phe stands for Phenolic and Azo stands for Azomethine. ^bThe theoretical wavenumbers were scaled by 0.9614.

mode vibrations of the complexes. This is because the DFT/B3LYP method tends to overestimate normal mode frequencies due to a combination of electron correlation effects and basis set deficiencies. Therefore, scaling factors have to be used to obtain a considerably better agreement with experimental data [11] [21] . In this study, the calculated frequencies were corrected with a scaling factor of 0.9614 which is appropriate for frequencies calculated by the DFT/B3LYP method [22] -[24] .

After scaling, we determined the correlation between experimental (FT-IR) and calculated wavenumbers of both AOYP and its transition metal complexes. The relation between these results is linear as described by the following correlation equations:

(R² = 0.985); for the AOYP ligand

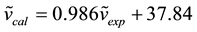(R² = 0.992); for M(II) complexes of AOYP

In the process of establishing the correlation equations, we used average wavenumbers for each of the normal modes, calculated from the wavenumbers of all the complexes and average values in a range for experimental wavenumbers. A comparison of the scaled wavenumbers calculated by the B3LYP/GEN method with experimental values reveals a very good agreement; with correlation coefficients of 0.985 and 0.992 for AOYP and its transition metal complexes respectively. The experimental IR frequency assigned to the phenolic O-H vibrational mode of AOYP is 3382 cm⁻¹, according to [3] . The frequency for this vibrational mode reported in [5] for the ligand 2-(5-mercapto-[1,3,4]-oxadiazol-2-yl)phenol which differs from AOYP only by the replacement of NH₂ (amino group) with SH (mercapto group), is 3219 cm⁻¹. The calculated frequency for the phenolic O-H stretching vibration is 3237 cm⁻¹, which is closer to the experimental value reported in [5] than that reported in [3] . The calculated frequency disagrees with the experimental value reported in [3] with a relative error of −4.28%. Equation (1) was used to calculate this relative error [25] .

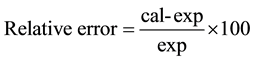(1)

In Equation (1), cal represents the calculated value and exp represents the experimental value. The vibrational frequency of the phenolic O-H disappeared in the spectra of all complexes. This indicates that the AOYP ligand coordinates to the central metal ion in each complex through the phenolic oxygen via deprotonation. The calculated frequency for the C=N stretching vibration in AOYP is 1582 cm⁻¹, which agrees very well with the experimental value since the relative error is only −0.94%. The calculated frequency undergoes a shift towards lower wavenumbers by 63 - 62 cm⁻¹ in the complexes. This is indicative of the coordination of one of the azomethine nitrogen atoms in the oxadiazole ring to the central metal ion.

The calculated IR frequency for the phenolic C-O vibration is 1259 cm⁻¹ in AOYP. This agrees very well with the experimental value. Contrary to experimental results, the theoretical band shifted to higher (instead of lower) wavenumbers by 91 - 79 cm⁻¹ in the complexes. In reality, a shift to lower wavenumbers is expected because the phenolic C-O bond length reduces from 1.35 Å in AOYP to 1.30 Å in the complexes. Also, the phenolic oxygen atom is involved in intensive hydrogen bonding with the H₂O ligands, which is not the case in the AOYP ligand. The presence of calculated IR bands in the range 3456 - 3399 cm⁻¹ in the spectra of the complexes due to stretching vibrations of O-H bonds in H₂O, indicate the presence of coordinated water or water of crystallization in the complexes. This is consistent with experimental results. Calculated IR bands due to the vibrations of O-H bonds in H₂O are completely absent in the spectrum of AOYP because it does not contain attached H₂O molecules.

The calculated IR spectra for AOYP and its transition metal complexes showed the persistence of two small bands in the region 3510 - 3259 cm⁻¹ corresponding to the stretching vibrations of N-H bonds in the NH₂ group. This suggests the non-coordination of the NH₂ groups to the central metal ion. However, the IR frequency corresponding to the vibrations of N-H bonds in the NH₂ group is shifted to lower wavenumbers by 150 cm⁻¹ in (B). This can be attributed to the strong hydrogen bonds formed between this group and the non-coordinated water molecules, which act as water of crystallization.

The calculated spectra of the complexes showed the appearance of new bands due to ῦ (M-N) and ῦ (M-O) metal-ligand vibrations in the regions; 550 - 419 cm⁻¹ and 419 - 335 cm⁻¹ respectively. This further confirms the participation of the phenolic oxygen atom and one azomethine nitrogen atom in coordination to the central metal ion. The M-L vibrational frequencies of these complexes are in good agreement with the experimental values reported in [5] . The IR spectra of the complexes indicate that AOYP behaves as a bidentate ligand and coordinates to the metal ion via the phenolic (O-H) group (after deprotonation) and the azomethine (C=N) group.

3.3. Frontier Molecular Orbital Analysis

Frontier molecular orbitals (FMOs) are the highest occupied molecular orbitals (HOMO) and the lowest-lying unoccupied molecular orbitals (LUMO) [26] . FMOs determine the way a given molecule interacts with other species and play a major role in governing many chemical reactions of molecules [27] . They also play an important role in electrical properties and UV-Vis spectra of chemical systems. The HOMO energy determines the ability of a compound to donate an electron while the LUMO energy determines its ability to accept an electron [28] [29] . Since frontier molecular orbital compositions, among other factors control optical and chemical properties, the compositions of the FMOs of (A), (B) and (C) that are predominantly involved in electronic transitions, have been calculated and discussed in detail. The frontier molecular orbital compositions of the complexes were calculated using the software package Multiwfn 3.3.6 [30] and are presented in Table 3. The molecular orbital (MO) compositions of (B) and (C) were calculated by the Hirshfeld method, while those of (A) were calculated by the Natural Atomic Orbital (NAO) method, taking Rydberg occupations into consideration [31] . The Hirshfeld method is more robust and convenient than the NAO method in computing MO compositions [30] . However, the NAO method was preferred in calculating the MO compositions of (A) because it allows the calculation of the compositions of the alpha and beta MOs separately; hence, it is more appropriate for open-shell systems. Electronic transitions in (A), an open-shell complex, were found to occur amongst the beta MOs, which are designated by letter “B” attached to the orbital indices in Table 3. The isosurfaces of the FMOs of the complexes generated using Gauss View 5.0.8, are visualized in Figures 4-6 for (A), (B) and (C) respectively.

The LUMO of each complex consists of π anti-bonding MOs designated by π*(AOYP), located on each of the two AOYP ligands, AOYP(1) and AOYP(2). The total contribution from the two AOYP ligands to the LUMO of (A) is 38.59%, to the LUMO of (B) is 33.93% and to the LUMO and LUMO + 1 each of (C) is 98.50%. In

^aB denotes a beta molecular orbital. ^bH represents HOMO and L represents LUMO. ^cM(II) represents the central metal ion which is Cu(II) for (A), Ni(II) for (B) and Zn(II) for (C).

addition, the LUMO of (A) and that of (B) have significant contributions from -orbitals on the central metal ions (61.35% from Cu²⁺ and 66.03% from Ni²⁺), denoted by d(Cu) and d(Ni) respectively. The HOMO of each complex comprises of π bonding MOs located on the AOYP ligands, designated as π(AOYP). Besides the contribution from AOYP, HOMO-5 in (A) has a 62.51% contribution from p orbitals on oxygen atoms in the H₂O ligands denoted p(O), while HOMO-8 and HOMO-15 in the same complex each have contributions from d(Cu) and p(O). Apart from the contribution from AOYP, all HOMOs of (B) also have contributions from d(Ni), the largest of which is 89.70% for HOMO-4. The HOMOs of (C) are almost entirely dominated by the AOYP ligands.

3.4. Electronic Absorption Spectra

In order to assign the already reported experimental electronic absorption bands of (A), (B) and (C) by [3] , TD-DFT calculations have been carried out on these complexes in DMSO at the B3LYP/GEN level of theory. TD-DFT is a useful method for studying excitation energies, and its application has increased in the recent years [32] . This method does give some errors in the excitation energies of charge-transfer states, however, better results may be obtained by using hybrid functionals which include a mixture of exact Hartree-Fock exchange with DFT exchange correlation [33] . The calculated electronic excitation energies and transition wavelengths (λ_cal) of the complexes, along with their oscillator strengths, assignments and transitions with significant coefficients of the wavefunction are listed in Table 4, together with the experimental transition wavelengths (λ_exp) obtained from [3] . These electronic transitions are elucidated in Figures 4-6 using the isosurfaces of the FMOs involved. Transition metal complexes generally show three types of electronic excitation bands which cover a wide wavelength range: d-d (crystal-field) transitions (300 - 1500 nm); metal-to-ligand charge-transfer (MLCT) and ligand-to-metal charge transfer (LMCT) transitions (200 - 500 nm); transitions localized on the ligands commonly known as intra-ligand charge transfer (ILCT) transitions, which regularly occur in the ultraviolet region [34] . ILCT results from n → π^* and n → π^* transitions and are affected by the type of coordination.

The scaling factor 0.72 was used to correct the calculated singlet-singlet electronic excitation wavelengths

^aWeight (%) of transition =, where c is the transition coefficient. ^bThe theoretical transition wavelengths were scaled with 0.72.

[25] . The electronic spectrum of (A) showed bands at 752 and 550 nm that can be attributed mainly to ligand- to-metal charge transfer transitions and a band at 446 nm with low oscillator strength (f = 0.0005), that is due to a d-d transition. The latter assignment was made since d-d transitions usually have very low intensities. The band at 550 nm with an oscillator strength of 0.0052, is the most intense and attributed to electronic excitation from HOMO-1 to LUMO. The HOMO-1 consists of 96.83% π(AOYP), whereas the LUMO is predominantly composed of 61.35% (Cu) + 38.59% π*(AOYP). This band, therefore, arises from the [π(AOYP)] → [d(Cu) + π*(AOYP)] transition, with a mixed LMCT and ILCT charge transfer character. The theoretical UV-Vis spectrum of (B) consists of three bands at 540, 463 and 395 nm with very low oscillator strengths (f = 0.0000), attributed mainly to d-d transitions. The three d-d bands can be assigned to ³A_2g(F) → ³T_2g(F), ³A_2g(F) → ³T_1g(F) and ³A_2g(F) → ³T_1g(P) transitions respectively, that correspond to the three characteristic spin allowed transitions of octahedral complexes [35] . This shows that (B) has a distorted octahedral geometry in which the two H₂O ligands that were initially directed along the z-axis are completely removed and solvent molecules occupy the vacant axial positions.

Each absorption band of (B) resulted from [d(Ni) + π(AOYP)] → [d(Ni) + π*(AOYP)] electronic transitions with a mixed character of d-d/MLCT/LMCT/ILCT. Experimental excitation energies were not reported for (C), given that it did not show any d-d transitions in the experimental spectrum. Theoretical electronic absorption bands at 243, 238 and 235 nm have been calculated for this complex and are found to result from ILCT transitions within the AOYP ligands. These bands occur principally due to π(AOYP) → π*(AOYP) electronic transitions. No d-d transitions were found in our calculations, confirming the experimental observation that d-d electronic transitions do not occur in Zn(II) complexes because the Zn(II) ion has a completely filled d sub-shell.

Comparing the experimental and calculated absorption spectra of the complexes, one can notice that both sets of data are in good agreement in terms of band positions, except for the first excited state (S₁) of (B) where a large discrepancy is observed between λ_cal (540 nm) and λ_exp (888 nm). The best agreement between experimental and theoretical absorption bands is observed for the S₃ excited state of (B) with λ_cal (395 nm) and λ_cal (371 nm).

3.5. Natural Bond Orbital (NBO) Analysis

NBO analysis [36] was carried out on the complexes under investigation in order to elucidate intramolecular charge transfer (ICT) and delocalization of electron density (ED) that result in their stabilization. NBO analysis is an efficient method for studying intra- and inter-molecular bonding and provides a convenient basis for investigating conjugative and hyperconjugative interactions in molecular systems, between occupied Lewis-type (bonding or lone pair) natural bond orbitals (NBOs) and formally unoccupied non-Lewis NBOs (anti-bonding or Rydberg) [20] [37] . Table 5 lists the occupancies and energies of the most important NBOs along with their percentage of hybrid atomic orbital contributions. Parenthesized label numbers in this table such as LP(2)O19 and LP*(6)Cu20 show the number of lone pair orbitals at each center; two lone pair orbitals on O19 and six on Cu20 respectively. The percentage of hybrid atomic orbital contributions of the bonding (σ and LP) NBOs of the complexes showed that they are mainly composed of both s-type and p-type orbitals. For instance, the bonding σ(C3-C11) NBO in (A) is formed from sp^2.25 on C3 (which is a mixture of 30.71% s and 69.24% p) and sp^1.35 on C11 (which is a mixture of 42.46% s and 57.50% p). Similarly, the bonding LP(1)N15 in (C) consists of sp^1.89 on N15 (which is a mixture of 34.62% s and 65.36% p). On the other hand, all anti-bonding NBOs are predominantly either p-type orbitals as is the case with the NBOs LP*(7) Zn20, LP*(8) Zn20 and LP*(9) Zn20 or s-type orbitals as in the NBOs LP*(6) Cu20 and LP*(6) Zn20.

The delocalization of ED between occupied Lewis-type and unoccupied non-Lewis NBOs correspond to stabilizing donor-acceptor interactions that contribute predominantly to the stabilization of the entire molecular system. The strength of these interactions can be estimated by the second order perturbation theory [38] [39] . For each donor (i) and acceptor (j) in the complexes, the stabilization energy or second-order perturbation energy, E⁽²⁾ associated with the delocalization from i → j was estimated using Equation (2). Values of this energy are proportional to the intensities of NBO interactions or to the extent of ICT within a molecular entity. The greater the electron donating tendency from donor to acceptor NBOs, the larger the E⁽²⁾ values and the more intense the interaction between the electron donors and the electron acceptors [37] [39] [40] .

(2)

^aLP(n)A generally represents a valence lone pair orbital (n) on atom A. For atomic numbering, refer to (A1), (B1) and (C1) in Figures 1-3 respectively. ^bPercentage contribution of atomic orbitals in NBO hybrid, given in their respective brackets.

In Equation (2), q is the donor orbital occupancy, ε_i and ε_j are diagonal elements (orbital energies) of donor and acceptor NBOs respectively and is the off-diagonal NBO Fock matrix element. The most intense interactions between “filled” (donor) Lewis type NBOs and “empty” (acceptor) non Lewis NBOs of the complexes are given in Table 6. The strongest interactions in (A) are: LP(1)C5 → π*(C1-C6), π*(C3-C4); π(C32-N36) → π*(C23-C24), π*(C34-N35); LP(1)C27 → π*(C25-C26); LP(2)O21 → LP*(1)C22; LP*(1)C2 → π*(C3-C4);

LP*(1)C22 → π*(C23-C24) and π*(C11-N15) → π*(C3-C4), producing a total of 337.57 kcal/mol stabilization energy. The most intensive interactions in (B) are: σ(O19-Ni20) → σ*(Ni20-N36), σ*(N15-Ni20); σ(Ni20-O21) → σ*(Ni20-N36), σ*(N15-Ni20); LP(1)C3 → LP*(1)C2, π*(C11-N15); LP(1)C23 → LP*(1)C22; LP(2)O19 → LP*(1)C2 and LP(2)O21→ LP*(1)C22, leading to total stabilization energy of 4737.14 kcal/mol. The strongest interactions in (C) are: LP(1)C3 → π*(C11-N15), LP*(1)C2; LP(1)C23 → π*(C32-N36), LP*(1)C22; LP(3)O19 → LP*(1)C2 and LP(3)O21 → LP*(1)C22, resulting in total stabilization energy of 3552.75 kcal/mol. The intense NBO interactions in (A) result in total stabilization energy that is far smaller than each of those in (B) and (C), suggesting less electron delocalization and consequently minimal ICT in (A). The results of NBO analysis reflect a generally charge transfer from lone pair orbitals located on the donor atoms O19, O21, N15, N36 on AOYP to the central metal ions, the benzene and oxadiazole rings. NBO analysis provides the most accurate possible “natural Lewis structure”. In each of the complexes, donor-acceptor interactions result in a loss of occupancy from “filled” localized NBOs of this “natural Lewis structure” into “empty” Non-Lewis orbitals. These interactions are observed as an increase in ED in σ and π anti bonding orbitals C-C, C-O, C-N and Ni-N, which weakens the respective bonds and results in ICT stabilization of the complexes.

3.6. Molecular Electrostatic Potential (MEP) Surfaces

To investigate reactive sites for electrophilic and nucleophilic attack, the MEP surfaces for (A)-(C) were plotted by DFT calculations over optimized geometries at the B3LYP/GEN level of theory in water as solvent. Water was chosen instead of DMSO for these calculations since most biological reactions occur in water. A MEP surface is an electron density isosurface mapped with an electrostatic potential surface. The MEP surfaces for the complexes (shown in Figure 7) can be used to determine their sizes, shapes, charge densities and reactive sites. Different values of electrostatic potential at the surfaces are represented by different colors; red represents regions of most negative electrostatic potential, blue represents regions of most positive electrostatic potential and green represents regions close to zero electrostatic potential. The electrostatic potential increases in the order: Red < Orange < Yellow < Green < Blue [28] [41] [42] . The negative (red and yellow) regions of the MEP surfaces are related to electrophilic reactivity and the positive (blue) regions to nucleophilic reactivity [10] [29] [43] . The most negative region of the MEP surface for each complex is mainly localized over the phenolic oxygen atoms, indicating that they are the most suitable atomic sites for electrophilic attack. The maximum positive region is localized on the N-H bonds of the groups, showing that they are possible sites for attack by nucleophiles. The MEP surfaces reveal that electron density is most evenly distributed in (B) and most unevenly distributed in (A). This explains why their dipole moments in water increase in the order: 2.2172 Debye for (B) > 2.6794 Debye for (C) > 2.8467 Debye for (A). It is equally clear from Figure 7 that the delocalization of the electron density of atoms in all complexes is primarily taking place within the benzene rings, since they correspond to a fairly reddish-yellow color on the MEP surfaces.

4. Conclusion

The ground state geometries, spectral (IR and UV-Vis) properties, natural bond orbital (NBO) analysis,

electrostatic potentials and frontier molecular orbital analysis of three complexes of 2-(5-amino-[1,3,4]-oxadi- azol-2-yl)phenol with Cu(II), Ni(II) and Zn(II) were investigated by DFT and TD-DFT methods. The complexes were optimized in the gas phase and solution phase at two levels of theory (B3LYP/LANL2DZ and B3LYP/ GEN) for comparison, after which B3LYP/GEN was chosen for all remaining calculations. The calculated IR wavenumbers were compared with the experimental values and a good agreement was found. The results of NBO analysis reflect charge transfer from lone pair orbitals located on the donor atoms O19, O21, N15 and N36 on 2-(5-amino-[1,3,4]-oxadiazol-2-yl)phenol to the central metal ions, as well as to the benzene and oxadiazole rings. The electrostatic potential surface of each complex showed that the highest electron density is on the phenolic oxygen atoms, indicating that they are the most suitable atomic sites for attack by electrophiles. The maximum positive region was found to be localized on the N-H bonds of the NH₂ groups, showing that they are possible sites for attack by nucleophiles. The theoretical electronic spectrum of (A) showed bands at 752 and 550 nm mainly attributable to ligand-to-metal charge transfer (LMCT) transitions and a band at 446 nm assigned to a d-d transition. The electronic spectrum of (B) consisted of three bands at 540, 463 and 395 nm mainly due to d-d transitions. Electronic absorption bands at 243, 238 and 235 nm were calculated for (C) and found to arise from intra-ligand charge transfer (ILCT) transitions within the 2-(5-amino-[1,3,4]-oxadiazol-2-yl)phenol ligand. A comparison of experimental and calculated absorption spectra of the complexes showed that both sets of data are in good agreement in terms of band positions.

Acknowledgements

The authors are thankful to the IIT Kanpur, India for the resources made available through a CV Raman International Fellowship award (Grant No. 101F102), offered to Julius Numbonui Ghogomu by the Ministry of External Affairs of India and FICCI (Federation of Indian Chambers of Commerce and Industry). They also wish to acknowledge the efforts of Dr. Matthew J. McGrath for proof reading this manuscript.

Cite this paper

Nyiang KennetNkungli,Julius NumbonuiGhogomu,Ludovid NgouoNogheu,Shridhar RamachandraGadre, (2015) DFT and TD-DFT Study of Bis[2-(5-Amino-[1,3,4]-Oxadiazol-2-yl) Phenol](Diaqua)M(II) Complexes [M = Cu, Ni and Zn]: Electronic Structures, Properties and Analyses. Computational Chemistry,03,29-44. doi: 10.4236/cc.2015.33005

References

NOTES

^*Corresponding author.