Computational Chemistry
Vol.02 No.02(2014), Article ID:44182,2 pages
10.4236/cc.2014.22003
Modeling Metal Binding Sites in Proteins by Quantum Chemical Calculations
Todor Dudev
Faculty of Chemistry and Pharmacy, University of Sofia, Sofia, Bulgaria
Email: t.dudev@chem.uni-sofia.bg
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Currently about half of all known proteins contain metal cofactors. Metal cations are indispensable components of the cellular machinery and are involved in a number of essential tasks ranging from nucleic acid and protein structure stabilization to enzyme catalysis, signal transduction, muscle contraction, hormone secretion, taste and pain sensation, respiration, and photosynthesis [1] -[3] . They are the simplest, but most versatile, cofactors in protein biochemistry with a plethora of distinctive properties, such as electron-acceptor ability, positive charge, flexible coordination sphere, specific ligand affinity, varying valence state, low- or high-spin configuration, and mobility.
Quantum chemical calculations have been extensively used to model active sites in metalloproteins and evaluate thermodynamic and/or kinetic parameters of the respective biochemical processes. These calculations are well suited for the task as they can capture all the electronic effects (including polarization and charge transfer effects between interacting entities) which are of paramount importance for properly describing the interactions between metal cations and protein ligands. Note that the polarization and charge transfer effects, which are poorly treated (if at all) in other computational approaches based on classical force fields, are quite significant and need to be explicitly accounted for especially in binding sites containing doubly (e.g. Mg2+ or Zn2+) or triply charged (Fe3+) metal cations.
In modeling studies usually the metal and its first and/or second ligation sphere are treated by high-level quantum chemical calculations, whereas the rest of the protein is subjected to either continuum dielectric calculations, molecular mechanics computations or lower basis set ab initio/DFT calculations. What is the succession and type of steps that should be undertaken in order to build up a realistic model of the protein binding site and achieve sound computational results? Firstly, the metal and its partner ligands should be properly modeled. For metals, it is quite important to correctly model their coordination number and symmetry of the respective protein or aqua complexes, and spin-state (for open-shell metals) as these factors, along with the metal charge, are among the major determinants of metal binding and selectivity in protein systems [4] . In the model ligand molecule, the chemical nature of the metal-coordinating protein residue should be preserved. Thus, acetate (CH3COO−) is a good model for the Asp side chain, while both acetate and propionate (CH3COO− and CH3CH2COO−) are appropriate models for the Glu side chain. On the other hand, however, formaldehyde (H2CO) or acetone (CH3COCH3), although both containing a carbonyl group, are not proper models for the backbone peptide group (-CO-NH-) or side chain of Asn and Gln (-CO-NH2) since the chemical and electronic properties of the amide group differ quite significantly from those of the aldehyde and ketone moieties, respectively. Along the same vein, ammonia (NH3) or aliphatic amine (CH3NH2) are not right models for the ligating −N= center of histidine, as the electron density within the His imidazole ring, due to conjugation effects, is quite different from that in ammonia and aliphatic amines.
Next step is the choice of appropriate level of theory for executing the calculations. Generally, this will depend on the size (number of atoms) of the protein system to be studied and computer resources available. Among different theoretical methods and basis sets which appear affordable for the user, however, the combination which best reproduces a set of experimental observables related to the protein system under study, should be chosen. There is a variety of experimental data suitable for calibrating the ab initio/DFT calculations, such as geometrical parameters (bond distances and valence angles) of metal complexes with water or simple organic/ inorganic ligands, gas-phase dipole moments and polarizabilities of protein ligands or their models, enthalpies/ free energies of protonation or deprotonation reactions in the gas-phase of given set of ligands, etc.
Biochemical reactions in proteins take place in condensed phase where the active site is located in a cavity/ crevice characterized by particular dielectric constant (varying from ~4 for buried binding sites to ~30 for solvent exposed binding pockets). Once the proper level of quantum chemical calculations for treating the metal and its immediate surroundings had been established (see above), the next step should be undertaken: the calibration of the condensed phase calculations. Experimental free energies of salvation in different solvents can be used for the calibration purposes. For performing continuum dielectric calculations, molecular parameters, such as effective atomic van der Waals radii or atomic charges, can be optimized in order to evaluate free energies of solvation that best reproduce the experimental observables.
Before proceeding to the actual calculations (“production run”), a rigorous test—the validation of the calculations—should be done. Experimentally well-characterized reaction in condensed phase which mimics the biochemical process of interest can be chosen and used for that purpose. Successful reproduction of the experimental quantities (within 1 - 2 kcal/mol for the energy/free energy, for example) is an indicator for the calculations’ reliability and robustness.
Modeling the process of Li+ → Mg2+ substitution in magnesium binding sites in proteins will be used to illustrate the procedure outlined above. The competition between Mg2+ and Li+ for the metal-binding site can be assessed by the free energy of the Li+ → Mg2+ exchange reaction:
 (1)
(1)
Received 10 February 2014; revised 12 March 2014; accepted 20 March 2014
In Equation (1), [Mq+-protein] and [Mq+-aq] represent the metal ion (Mq+ = Mg2+ or Li+) bound to protein ligands and unbound in the vicinity of the binding cavity, respectively. The metal and its first ligation sphere are treated by quantum chemical methods, while the rest of the protein is modeled as continuum dielectric characterized by a given dielectric constant.
In protein binding sites Mg2+ is usually bound to the side chains of Asp/Glu or Asn/Gln, or the backbone peptide group [5] . Accordingly, the side chains of Asp/Glu, Asn/Gln, and peptide backbone group are modeled as acetate (CH3COO−), acetamide (CH3CONH2), and N-methylacetamide (CH3CONHCH3), respectively. In proteins as in aqueous solution Mg2+ is mostly hexacoordinated [6] [7] . Thus, Mg2+ complexes are modeled as MgL6 (L = H2O, CH3CONH2, CH3CONHCH3, CH3COO−). The most common coordination number of Li+ is four [8] . Accordingly, its complexes are modeled as LiL4.
The B3LYP/6-31+G(3d, p) method/basis set combination is chosen among various other combinations as it best reproduces the experimental dipole moments, µ, of model ligands and metal―ligand bond distances, R, in metal complexes [9] [10] :
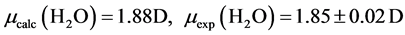
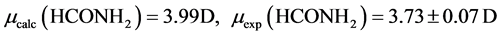
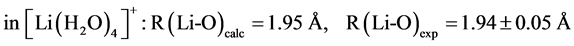 ,
,
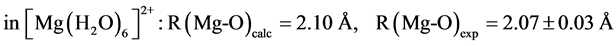 .
.
Condensed-phase calculations are calibrated with respect to experimental free energies of hydration of the metal cations and model ligands. Results are given in Table 1. For validation purposes, the experimental free energies of Li+ → Mg2+ substitution in acetate, oxalate and nitrilotriacetic acid complexes are used and com-
Table 1. Comparison between computed and experimental hydration free energies,  , of metal cations and model ligands (in kcal/mol) [9] .
, of metal cations and model ligands (in kcal/mol) [9] .

Table 2. Comparison Between Computed and Experimental Free Energies (in kcal/mol) for [MgX] + [Li(H2O)4]+ → [LiY] + [Mg(H2O)6]2+ in Water, ΔG80 (Li+ → Mg2+) [9] .
aError = ΔG80(Calc) − ΔG80(Exp). bNTA = nitrilotriacetic acid bound in a tetradentate fashion (including central N atom) to the metal.
pared with those evaluated theoretically using the models and methods described above. As seen from the results presented in Table 2, the calculations reproduce the experimentally determined free energies of Li+ → Mg2+ substitution within1 kcal/mol. Now, avenues are open for the “production run”.
References
- Frausto da Silva, J.J.R. and Williams, R.J.P. (1991) The Biological Chemistry of the Elements. Oxford University Press, Oxford.
- Lippard, S.J. and Berg, J.M. (1994) Principles of Bioinorganic Chemistry. University Science Books, Mill Valley.
- Bertini, I., Sigel, A. and Sigel, H. (2001) Handbook on Metalloproteins. Marcel Dekker, New York.
- Dudev, T. and Lim, C. (2014) Competition among Metal Ions for Protein Binding Sites: Determinants of Metal Ion Selectivity in Proteins. Chemical Reviews, 114, 538-556. http://dx.doi.org/10.1021/cr4004665
- Dudev, T., Lin, Y.-L., Dudev, M. and Lim, C. (2003) First-Second Shell Interactions in Metal Binding Sites inProteins: A PDB Survey and DFT/CDM Calculations. Journal of the American Chemical Society, 125, 3168-3180. http://dx.doi.org/10.1021/ja0209722
- Jernigan, R., Raghunathan, G. and Bahar, I. (1994) Characterization of Interactions and Metal-Ion Binding Sites in Proteins. Current Opinion in Structural Biology, 4, 256-263. http://dx.doi.org/10.1016/S0959-440X(94)90317-4
- Marcus, Y. (1988) Ionic Radii in Aqueous Solutions. Chemical Reviews, 88, 1475-1498. http://dx.doi.org/10.1021/cr00090a003
- Dudev, M., Wang, J., Dudev, T. and Lim, C. (2006) Factors Governing the Metal Coordination Number in Metal Com- plexes from Cambridge Structural Database Analyses. Journal of Physical Chemistry B, 110, 1889-1895. http://dx.doi.org/10.1021/jp054975n
- Dudev, T. and Lim, C. (2011) Competition between Li+ and Mg2+ in Metalloproteins. Implications for Lithium Therapy. Journal of the American Chemical Society, 133, 9506-9515. http://dx.doi.org/10.1021/ja201985s
- Dudev, T. and Lim, C. (2009) Determinants of K+ vs Na+ Selectivity in Potassium Channels. Journal of the American Chemical Society, 131, 8092-8101. http://dx.doi.org/10.1021/ja900168k


