Received 12 October 2014; revised 13 November 2014; accepted 29 November 2014

ABSTRACT

Conjunction of two probability laws can give rise to a possibility law. Using two probability densities over two disjoint ranges, we can define the fuzzy mean of a fuzzy variable with the help of means two random variables in two disjoint spaces.

Keywords:

Probability Density Function, Probability Distribution, Fuzzy Measure, Fuzzy Expected Value, Fuzzy Mean, Fuzzy Membership Function, Dubois-Prade Reference Functions

1. Introduction

Zadeh [1] introduced the concept of fuzziness into the realm of mathematics. Accordingly, various authors have studied the mathematics related to the fuzzy measure and the associated fuzzy expected value [2] -[7] studied the fuzzy expected value and its associated results by defining the fuzzy expected value in terms of fuzzy measure. In their definition they tried to find the fuzzy expected value of a possibility distribution. In [8] , authors developed a new method of analysis of possibilistic portfolio that associates a probabilistic portfolio. Similar works were done in associating possibility and probability [9] [10] . In [11] [12] , the author tries to establish a link between possibility law and probability law using a concept discussed in the paper called set superimposition [13] . In [14] , the author tries to establish a link between and randomness.

In this article, using the superimposition of sets, we have attempted to define the expected value of a fuzzy variable in term of expected values of two random variables in two disjoint spaces. It can be seen that the expected value of a fuzzy number is again a fuzzy set.

2. Definitions and Notations

Let be a continuos random variable in the interval with probability density function 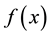and probability distribution function. Then

Further, the expected value of 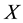would be

(1)

where the integral is absolutely convergent.

Let 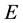be a set and 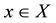then we can define a fuzzy subset 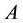of as

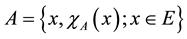
where 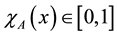is the fuzzy membership function of the fuzzy set 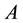for an ordinary set, or 1.

A fuzzy set is called normal if for at least one.

A -cut for a fuzzy set is an ordinary set of elements such that for, i.e..

The membership function of a fuzzy set is known as a possibility distribution [15] . We usually denote a fuzzy

number by a triad such that and., for, is the left reference function and for is the right reference function. The left reference function is right conti-

nuous, monotone and non-decreasing, while the right reference function is left continuous, monotone and non- increasing. The above definition of a fuzzy number is known as an L-R fuzzy number.

Kandel’s Definition of a Fuzzy Measure

Kandel [5] [16] has defined a fuzzy measure as follows: Let be a Borel field (-algebra) of subset of the real line. A set function defined on is called fuzzy measure if it has the following properties:

(1) (is the empty set);

(2);

(3) If with, then;

(4) If is a monotonic sequence, then Clearly,. Also, if, then. is called a fuzzy measure space. is the fuzzy measure of.

Let and. The function is called a -measurable function, if for all. In their notations, fuzzy expected value is defined as follows: Let be a - measurable function such that. The fuzzy expected value (FEV) of over a set with respect to the measure is defined as.

Now is a function of the threshold. The calculation of FEV then consists of finding the intersection of the curves of. The intersection of the curves will be at a value so that FEV as in the diagram.

3. Definition of an Expected Value of Fuzzy Number

Kandel’s definition of a fuzzy expected value is based on the definition of the fuzzy measure. However, the fuzzy measure being non-additive is not really a measure.

Baruah [13] has shown that instead of expressing a fuzzy measure in, if we express the possibility distribution first as a probability distribution function in and then as a complementary probability distribution function in, the mathematics can be seen to be governed by the product measure on and. As such, the question of non-additivity of the fuzzy measure does not come into picture.

We propose to define the fuzzy expected value or the possibilistic mean based on the idea that two probability measures can give rise to a possibility distribution. In other words, the concerned possibilistic measure need not be fuzzy at all.

Accordingly, we propose to define a possibilistic mean as follows: Let be a fuzzy variable in the fuzzy

set. We divide into two intervals and such that and. Let be a random variable on. Then from (1), the mean of would be

(2)

where is the concerned probability density function defined on. Let the mean of the random variable an be

(3)

where is the concerned probability density function defined on.

Thus, from (2) and (3), we get the possibilistic mean of as

(4)

where.

Equation (4) is our required result that shows that poissibilistic mean of a fuzzy variable is again a fuzzy set.

To illustrate the result (4), we take, a triangular number such that and. The probability distribution function is given by

(5)

where

(6)

is the probability density function in.

The complementary probability distribution or the survival function is given by

(7)

where and the probability density function in is

(8)

Therefore, the expected value of a uniform random variable on is

(9)

and similarly, the expected value of another uniform random variable on is

(10)

Equations (9) and (10) together give the expected value of a triangular fuzzy variable in as

(11)

where.

Equations (4) and (11) show that the expected value of a fuzzy number is again a fuzzy set.

4. Conclusion

The very definition of a fuzzy expected value as given by Kandel is based on the understanding that the so called fuzzy measure is not really a measure in the strict sense. The possibility distribution function is viewed as two reference functions. Using left reference function as probability distribution function and right reference function as survival function, in this article we redefine the expected value of a fuzzy number which is again a fuzzy set.

References