International Journal of Intelligence Science
Vol.04 No.04(2014), Article ID:50243,9 pages
10.4236/ijis.2014.44010
Method to Improve Airborne Pollution Forecasting by using Ant Colony Optimization and Neuro-Fuzzy Algorithms
Elizabeth Martinez-Zeron1, Marco A. Aceves-Fernandez1*, Efren Gorrostieta-Hurtado1, Artemio Sotomayor-Olmedo2, Juan Manuel Ramos-Arreguín1
1Facultad de Informática, Universidad Autónoma de Querétaro, Querétaro, México
2Laboratory of Artificial Intelligence, Faculty of Engineering, Universidad Autónoma de Querétaro, Querétaro, México
Email: *marco.aceves@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 August 2014; revised 5 September 2014; accepted 12 September 2014
ABSTRACT
This contribution shows the feasibility of improving the modeling of the non-linear behavior of airborne pollution in large cities. In previous works, models have been constructed using many machine learning algorithms. However, many of them do not work for all the pollutants, or are not consistent or robust for all cities. In this paper, an improved algorithm is proposed using Ant Colony Optimization (ACO) employing models created by a neuro-fuzzy system. This method results in a reduction of prediction error, which results in a more reliable prediction models obtained.
Keywords:
Neuro-Fuzzy models, Ant Colony Optimization, Airborne Pollution

1. Introduction
In recent years, the environment has been affected by the presence of particulate pollutants such as the Ozone (O3), NO2 nitrogen oxide, carbon monoxide CO, sulfur dioxide (SO2) and particulate matter less than 10 microns PM10 (≤10 microns) and Particles less than 2.5 micrometers PM2.5 (≤2.5 microns) [1] . For this reason, pollution monitoring has been necessary for large cities with high concentration of population and industries.
During several years the air quality in Mexico City for prevention of toxicity levels in health and the environment have been observed and evaluated [1] .
Measures were performed to obtain information efficiency and reliability of the air quality. Some of these contributions consists in predicting pollution levels such as the work of Cortina [2] , who forecast levels of ozone pollution in the city of Guanajuato in Mexico by using neural networks, Aceves [3] takes modeling variables between relative humidity and temperature level of contamination. Sotomayor [4] uses support vector machines and kernel functions particulate ozone (O3), (PM10) and nitrogen dioxide in Mexico City.
Patterns of pollution levels do not show linear behavior [3] [4] whereby a pattern is generated in clusters can be represented by several linear functions, this for ease of interpretation. In this case study, Fuzzy C means is used to generate clusters which have similar characteristics, subsequently establish the cluster centers as membership functions in a fuzzy system [3] , Also, neuro-fuzzy inference system (ANFIS) with multiple inputs and one output (“Multiple-Inputs-Single-Output” or MISO) is used to approximate nonlinear functions [5] [6] . Subsequently, three models are generated by the above steps after obtaining improved by using the algorithm of ant colony optimization (ACO) prediction. This methodology shows that it is possible to improve existing algorithms to predict the levels of particulate pollutants, in this case study in Mexico City.
1.1. Fuzzy inference methods
A Fuzzy Inference System (FIS) is basically a logic that allows intermediate values defined between conventional evaluations as Yes/No, True/False, etc.
A FIS is the main unit of a fuzzy logic system, the part where the decision is made, by constructing appropriate rules based on the theory of fuzzy sets. The rules are constructed linguistically (IF-THEN-) having the general form of “If A Then B” where A and B are (collections of) propositions containing linguistic variables linked by connectors (AND, OR) to make the correct decision-making [7] .
A fuzzy inference system consists of 5 blocks as described in Figure 1.
Fuzzy inference system operates as follows: The input data are treated by a method of fuzzification then the Fuzzy rules are formed and the already fuzzyfied input data are analyzed. Defuzzification method is used to convert the value obtained after analysis with fuzzy rules to obtain an output value applicable to the real world.
The steps taken by fuzzy reasoning, i.e. inference operations on rules IF - THEN performing the FIS, are:
· Compare the input variables with the membership functions for the linguistic value of each part, this process is called fuzzyfication.
· Combine by an operator (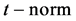 , usually multiplication or minimum) the membership values to obtain the weight of each rule.
, usually multiplication or minimum) the membership values to obtain the weight of each rule.
· Add the resulting output to produce a crisp, this step is called defuzzification.
A fuzzy rule has a general structure in a fuzzy model as shown on equation (1):
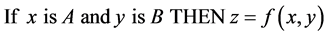 (1)
(1)
where 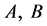 fuzzy sets in the previous data sets are,
fuzzy sets in the previous data sets are,  is a consequent function. Usually
is a consequent function. Usually 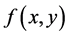 is polynomial in the input variables
is polynomial in the input variables 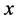 and
and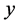 , the output of the system with a fuzzy region specified by the predecessors of the rule.
, the output of the system with a fuzzy region specified by the predecessors of the rule.
Figure 1. Block Diagram of a Generic Fuzzy inference system.
A typical rule in FIS model has the form as shown in equation (2) [8] :
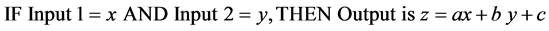 (2)
(2)
The final output of the FIS system is the weighted average of all the outputs of the rules:
 (3)
(3)
The Takagi-Sugeno model or TSK model proposed in 1985 [8] [9] , is widely used in the theoretical analysis, application control and Fuzzy Modeling.
A Fuzzy system needs a precedent and consequent to express a logical connection between the input and output data used as a basis to produce the desired behavior of the system.
1.2. Clustering
Clustering is the grouping of data based on certain criteria that clusters have similar properties and characteristics, clusters are based mainly on the distance interpreted as similarity [10] .
1.2.1. Fuzzy C-means
Fuzzy C-Means (FCM) is a clustering method which allows a data to belong in one or more clusters, this method developed by Dunn [11] and improved by Bezdek [10] , is often used for pattern recognition, it is an iterative optimization algorithm that minimizes the cost function given by:
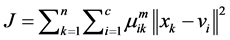 (4)
(4)
where 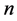 is the number of data,
is the number of data, 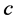 is the number of clusters,
is the number of clusters,  is the
is the 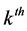 data point,
data point, 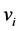 is the center of the
is the center of the 







Starting with the desired number of cluster 





To measure the effect of clustering algorithm, validity and accuracy are required. Validity: If the algorithm can find all internal type in the data collected. Truth: If the algorithm can set the same kind of data to the same group, different types of data at different clusters. We define the rate of decline of Clustering 




After determining the number of clusters, the value of m, and the stopping criterion the FCM algorithm performs two steps, first calculates the membership functions using equation (5), as a second step updates the proto types using equation (7) the two steps are repeated iteratively to achieve the stability criterion, in which the change of the output values by the previous equations is minimal. The Figure 2 shows an example FCM function.
Figure 2. Example of Fuzzy C-Means showing three different clusters with a set of data points each, and their centroids.
1.3. The Adaptive Neuro-Fuzzy Inference System (ANFIS)
This method is a type of neural network that is based on a method for the process of fuzzy modeling to learn information about a data set by generating fuzzy rules, this is called neuro-fuzzy, this architecture was proposed by Jang in 1993 [12] . Has a network structure with directional links connecting a number of nodes. Each node has a function with adjustable or fixed parameters.
The classical ANFIS consists of 5 layers with specific tasks as show in Figure 3 [13] .
First Layer (Layer 1). Layer one is performed the input fuzzification. That is, each entry will set a value of belonging that only covers the total of the input variables to be treated [13] . This is expressed in mathematical terms as follows:

While:




While the parameters 
Second Layer (Layer 2 from Figure 3). Executes the fuzzy AND of the antecedent part of the fuzzy rules. This results to each node’s output being the product of all of its inputs (every input term node that is connected to that rule node) [14] :

For all the terms nodes 

Third layer (Layer 3 from figure 3). Normalizes the membership functions (MFs).
The output of the 

Fourth layer (Layer 4 from figure 3) executes the consequent part of the fuzzy rules. Each node 


Figure 3. ANFIS architecture.
The weight 

Layer 5 computes the output of fuzzy system by summing up the outputs of layer fourth.

1.3.1. Optimization
The optimization algorithm is a numerical method which finds a value





As mentioned in [15] the techniques used for providing solution to complex combinatorial optimization problems have evolved from constructive methods to local search methods and finally to population-based algorithms. These techniques are classified as: Extensive and not exhaustive. These non-analytical computational techniques are based, and the classification is performed based on the solution space.
Exhaustive optimization techniques are those that guarantee always find the optimal (maximum or minimum) walking in the worst case the whole solution space (which can be considerably large) [16] .
Non-exhaustive techniques rely on getting good enough solutions without exceeding the time constraints established or memory. Solutions are based on steps taken to find new solutions that approximate the optimal solution more, increasing quality.
Some of the best known are:
· Genetic Algorithms
· Taboo search
· Ant Colony Optimization
· Greedy Randomized Adaptive Search Procedure (GRASP).
· Scatter Search
· Simulated Annealing
1.3.2. Ants Colony Optimization
The ant colony optimization (ACO) is a bio-inspired technique of classification based on the external behavior of a real ant colony when foraging. This algorithm was created in 1992 by Dorigo [17] .
The ACO algorithm solves complex problems of combinatorial optimization in various fields of engineering, commerce, industry, among others. When a problem does not have a polynomial equation that describes it belongs to the NP-hard problems. The results provided by ACO can be approximated to address the combinatorial optimization problemsas shown in the Figure 4. [18] .
The probability of an ant 


Figure 4. Example of ACO where ants choose the shortest path from node 1 to node 2.

where:





Updated Trail
Pheromone must be updated because this changes which followed the iterations by offering increased likelihood based on the accumulated experience [19] .
In this case the level of pheromone raises based on the best solution path according to equation (14)

where: 

Accumulating trace is proportional to the quality of solutions.



Every time an ant travels a node applies the rule:


The stop condition
This process is iterative until it stops for compliance with established criteria
2. Methodology
In Figure 5, the environmental monitoring map shown in Mexico City, in this study we only evidence in the northwest area of the spring season.
The list of the sites used in this contribution is shown on figure 5, whilst the proposed methodology for this contribution is shown in the figure 6.
The monitoring stations used for this case study were chosen due to data availability and specific industrial or polluted areas.
Since obtaining data from such stations is filtered data, i.e., data values are complete and validated readings
Figure 5. Monitored areas.
are sought.
The data are arranged in time series along the day; hence the clustering is performed to generate the characteristics of groups depending on pollution levels. These are grouped according through the fuzzy 
The fuzzy system is improved with training data, which in this case, the training data are data from a previous year validated dataset. The training is through the use of neuro-fuzzy system AN-FIS which generates a more robust data modeling system.
The training is carried out using of neuro-fuzzy system ANFIS which generates a more robust data modeling system.
Three models for the prediction of air quality are generated; these models are subject to the ant colony optimization algorithm to improve the prediction closer to an outcome more accurately. Such three models along with the real measured data and its corresponding prediction are shown on Figure 7.
The mean square error for each model generated with neuro-fuzzy and neuro-fuzzy with ACO to measure the difference between the estimated and the model.
3. Results and discussion
The models are created using Fuzzy Logic where the rules are formed by clustering, the ANFIS to improve each model and make each one more accurate and the ACO algorithm use these three models to improve the forecast
Figure 6. Proposed methodology.
Figure 7. Model selection by ACO.
having different options base on the three previous models. The models are named Mod 2 Mod 1 and Mod 3, respectively. These models are generated based on the characteristics of the stations, i.e. stations show greater similarity between their measurements generate a model.
The results are shown on table 1 and table 2. CO is sensed to the northwest, with three models generated
Table 1. Results of spring in northwestern federal district with CO pollutant.
Table 2. Results of spring in northwestern federal district with O3 pollutant.
based on the area in 2009, and data validation are the stations belonging to the same area but in 2010. Likewise the table 2 is showing the models of Ozone (O3). In the following tables the mean square error, it can be seen that is closer to the real value, the prediction of stations Station 1, Station 2, Station 3 and Station 4 based Mod 1, Mod 2 and Mod 3 models. The station in which there was no good approximation was at Station 1.
Figure 7 shows how the algorithm is based on the nearest location from the current node to the next node following the ACO algorithm as shown on equations (14)-(16) and the methodology shown on figure 6. The influence of the pheromone that can choose the model that is closest to the actual data, likewise considering also the shortest distance.
The figure 7 shows the comparison between the models created by the trained logic system with ANFIS and the ACO model. This to appreciate the difference between the accuracy for each model generated with neuro- fuzzy and neuro-fuzzy improved with ACO.
4. Conclusions
The algorithms based on swarm intelligence are feasible for solving problems different than the typical machine learning methods. It has shown that a combination of modeling and optimization methods may be used to improve the prediction for this type of non-linear problem. Such combination of methods showed that systems working cooperatively is well complemented and integrated to generate a task system.
For these reasons ACO is an algorithm that provides an improvement in the prediction of contamination if used properly. ACO prediction has a point of view on the combinatorial type issue, and thus, the use of this algorithm improves the contaminants prediction by making the shortest search and the use of pheromone provides a best approximation to real data.
Acknowledgements
This work was made possible through funding provided by the National Council of Science and Technology CONACYT.
References
- http://www.calidadaire.df.gob.mx/calidadaire/index.php?opcion=4&opcionrecursostecnicos=3
- Cortina. M. (2012) Aplicación de inteligencia artificial a la predicción de contaminantes atmosféricos. Tesis Doctoral, E.T.S.I. Telecomunicación (UPM).
- Aceves-Fernández, M.A., Sotomayor-Olmedo, A., Gorrostieta-Hurtado, E., Pedraza-Ortega, J.C., Tovar-Arriaga, S. and Ramos-Arreguin, J.M. (2011) Performance Assessment of Fuzzy Clustering Models Applied to Urban Airborne Pollution. 2011 21st International Conference on Electrical Communications and Computers (CONIELECOMP), San Andres Cholula, 28 February-2 March 2011, 212-216.
- Sotomayor-Olmedo, A., Aceves-Fernández, M.A., Gorrostieta-Hurtado, E., Pedraza-Ortega, C., Ramos-Arreguín, J.M. and Vargas-Soto, J.E. (2013) Forecast Urban Air Pollution in Mexico City by Using Support Vector Machines: A Kernel Performance Approach. International Journal of Intelligence Science, 3, 126-135. http://dx.doi.org/10.4236/ijis.2013.33014
- (2005) Adaptive Neuro-Fuzzy Inference Systems (ANFIS). In: Nedjah, N. and de Macedo Mourelle, L., Eds., Fuzzy Systems Engineering: Theory and Practice. Vol. 181, Springer, Rio de Janeiro, 53-83.
- Adaptive Neuro-Fuzzy Inference Systems (ANFIS) Library for Simulink Ilias S. Konsoulas M.Sc., CEng, MIET.
- Aceves-Fernandez, M.A., Sotomayor-Olmedo, A., Gorrostieta-Hurtado, E., Pedraza-Ortega, J.C., Ramos-Arreguín, J.M, Canchola-Magdaleno, S. and Vargas-Soto, E. (2011) Advances in Airborne Pollution Forecasting Using Soft Computing Techniques. In: Popovic, D., Ed., Air Quality: Models and Applications, INTECH Publisher, Querétaro, 1-14. http://dx.doi.org/10.5772/16273
- Sugeno, M. and Kang, G.T. (1988) Structure Identification of Fuzzy Model. Fuzzy Sets and Systems, 28, 15-33. http://dx.doi.org/10.1016/0165-0114(88)90113-3
- Takagi, T. and Sugeno, M. (1985) Fuzzy Identification of Systems and Its Application to Modeling and Control. IEEE Transactions on Systems, Man and Cybernetics, SMC-15, 116-132.
- Bezdek, J.C. (1981) Pattern Recognition with Fuzzy Objective Function Algoritms. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4757-0450-1
- Dunn, J.C. (1973) A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics, 3, 32-57. http://dx.doi.org/10.1080/01969727308546046
- Jang, J.S.R. (1993) ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Transactions on Systems, Man and Cybernetics, 23, 665-685.
- Ghanbari, A., Abbasian-Naghneh, S. and Hadavandi, E. (2011) An Intelligent Load Forecasting Expert System by Integration of Ant Colony Optimization, Genetic Algorithms and Fuzzy Logic. 2011 IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Paris, 11-15 April 2011, 246-251.
- Adaptive Neuro-Fuzzy Inference Systems (ANFIS) Library for Simulink
- Muñoz, M., López, J. and Caicedos, E. (2008) Inteligencia de enjambres: Sociedades para la solución de problemas (una revisión). Ingeniería e Investigación, 28, 119-130.
- Carretero, J.C.O., Cánovas, D.G. and Pereira, F.D.Q. (2008) Técnicas Heurísticas para Problemas de Diseño en Telecomunicaciones.
- Dorigo, M. (1992) Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Italian.
- Calixto, C.A.C. (2005) Implementacion En Hidroinformática De Un Método De Optimización Matemática Basado En La Colonia De Hormigas. Tesis no publicada, Pontificia Universidad Javeriana, Bogota, Colombia.
- Kole, A., Chakrabarti, P. and Bhattacharyya, S. (2013) An Ant Colony Optimization Algorithm for Uncapacitated Facility Location Problem.
NOTES
*Corresponding author.













