International Journal of Intelligence Science
Vol.4 No.3(2014), Article
ID:47574,5
pages
DOI:10.4236/ijis.2014.43008
Realization of Rough Set Approximation Toplogical Operations Based on Formal Concept Analysis
Huilai Zhi
School of Computer Science and Technology, Henan Polytechnic University, Jiaozuo, China
Email: zhihuilai@126.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 24 April 2014; revised 20 May 2014; accepted 3 June 2014
ABSTRACT
There is an intimate correlation between rough set theory and formal concept analysis theory, so rough set approximations can be realized by means of formal concept analysis. For any given multiple valued information system, the realization of rough set approximation operation has two major steps, firstly convert the information system from multiple valued one to single valued formal context, secondly realize rough set approximation operations aided by concept lattice, which is equivalent to a query operation under some necessary conditions.
Keywords:Rough Set, Approximation Operation, Formal Context, Concept Lattice

1. Introduction
Rough set theory (RS), first described by a Polish computer scientist Zdzisław I. Pawlak [1] , is a formal approximation of a crisp set (i.e., conventional set) in terms of a pair of sets which give the lower and the upper approximation of the original set. In the standard version of rough set theory, the lowerand upper-approximation sets are crisp sets, but in other variations, the approximating sets may be fuzzy sets. Formal concept analysis (FCA) is a principled way of automatically deriving ontology from a collection of objects and their properties [2] . The term was introduced by Rudolf Wille in 1984, and built on applied lattice and order theory that was developed by Birkhoff and others in the 1930s.
Research about the relationship between formal concept analysis and rough set theory has gained some development. Kent [3] and Yao [4] bring upper approximation and lower approximation in rough set theory into formal concept analysis, and discuss many approximation operators based on formal concept analysis. Qu Kaishe [5] focuses on the theory research about the correlation between formal concept analysis and rough set. He first reveals limitations of data analysis and processing in the rough set theory, and then provides a way for the synthesis of formal concept analysis and rough set theory by using nominal scale.
In these studies, the link between rough set theory and concept lattice is pointed out, but in practice how to realize the operation of rough set by using concept lattice is still left as a problem. Therefore, in this article, we focus on the way to realize rough set approximation topological operations based concept lattice, which includes upper approximation and lower approximation.
2. About Rough Set Theory and FCA
2.1. Basic Concepts in Rough Set Theory
Indiscernibility Relation is a central concept in rough set theory, and is considered as a relation between two objects or more, where all the values are identical in relation to a subset of considered attributes. Indiscernibility relation is an equivalence relation, where all identical objects of set are considered as elementary [6] .
Approximations is also other an important concept in Rough Sets Theory, being associated with the meaning of the approximation topological operations [7] . The lower and the upper approximations of a set are interior and closure operations in a topology generated by the indiscernibility relation. Below is resented and described the types of approximations that are used in Rough Sets Theory.
a) Lower Approximation 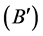
Lower Approximation is a description of the domain objects that are known with certainty to belong to the subset of interest. The Lower Approximation Set of a set![]() , with regard to
, with regard to 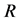 is the set of all of objects, which certainly can be classified with
is the set of all of objects, which certainly can be classified with ![]() regarding
regarding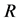 , that is, set
, that is, set![]() .
.
Formally, 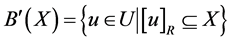
b) Upper Approximation 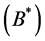
Upper Approximation is a description of the objects that possibly belong to the subset of interest. The Upper Approximation Set of a set ![]() regarding
regarding 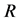 is the set of all of objects which can be possibly classified with
is the set of all of objects which can be possibly classified with ![]() regarding
regarding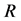 , that is, set
, that is, set![]() .
.
Formally, 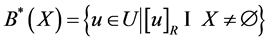 ,
, ![]() denote an empty set.
denote an empty set.
c) Boundary Region (BR)
Boundary Region is description of the objects that of a set ![]() regarding
regarding 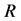 is the set of all the objects, which cannot be classified neither as
is the set of all the objects, which cannot be classified neither as ![]() nor
nor 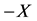 regarding
regarding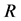 . If the boundary region is a set
. If the boundary region is a set![]() , then the set is considered “Crisp”, that is, exact in relation to
, then the set is considered “Crisp”, that is, exact in relation to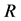 ; otherwise, if the boundary region is a set
; otherwise, if the boundary region is a set ![]() the set
the set ![]() “Rough” is considered. In that the boundary region is BR.
“Rough” is considered. In that the boundary region is BR.
Formally,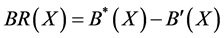 .
.
2.2. Basic Concepts in Formal Concept Analysis
Formal concept analysis, which is proposed by R. Wille, is founded on a basis of order theory and lattice theory, and is a mathematical structure which depicts relationship between objects and attributes according to basic information provided by data base. Formal concept analysis has been successfully used in many fields, and to some extend it has been treated as a means of external cognition [8] .
Definition 1: Given a formal context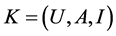 ,
, 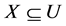 ,
, 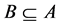 , if
, if ![]() and
and 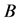 satisfy
satisfy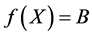 ,
, 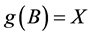 , and
, and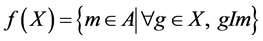 ,
, 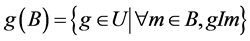 , we call the pair
, we call the pair 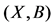 is a concept of formal context
is a concept of formal context![]() .
. ![]() is called extent of concept
is called extent of concept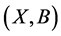 ,
, 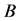 is called intent of concept
is called intent of concept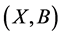 .
. 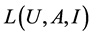 or
or 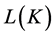 is the set which contains of the concepts of
is the set which contains of the concepts of ![]() [2] .
[2] .
Definition 2: Given a formal context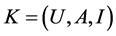 ,
, 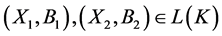 , if
, if 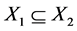 or
or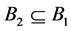 , then call
, then call 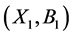 is a son concept of
is a son concept of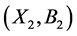 , and denote as
, and denote as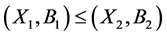 . Apparently,
. Apparently, 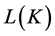 forms a lattice, which is called concept lattice [2] .
forms a lattice, which is called concept lattice [2] .
Given two concepts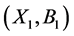 ,
, 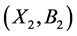 of a formal context
of a formal context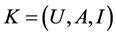 , we have: If
, we have: If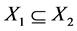 , then
, then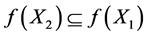 , for
, for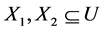 ; If
; If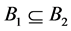 , then
, then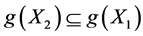 , for
, for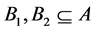 .
.
3. Realization of Approximation Operation Based on FCA
Realization of rough set approximation operation can be divided into two steps: first, convert multiple valued information system to multiple valued formal context, and then covert multiple value formal context to single value formal context; second, realize rough set approximation operation by using the technique of formal concept analysis based on concept lattice.
3.1. Convert Multiple Valued Is from to Single Valued Formal Context
In an information system ,
,  is the set of attributes, for every attribute
is the set of attributes, for every attribute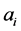 , if the value of
, if the value of 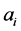 belongs to
belongs to  in which 1 represents an object has this attribute and 0 represents an object doesn’t has this attribute, then this information system corresponds to an single value formal context. Otherwise, if the value of
in which 1 represents an object has this attribute and 0 represents an object doesn’t has this attribute, then this information system corresponds to an single value formal context. Otherwise, if the value of 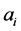 belongs to a set
belongs to a set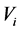 , and the size of
, and the size of 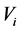 is greater than 2, then we have to convert this attribute to several attributes according to the size of
is greater than 2, then we have to convert this attribute to several attributes according to the size of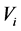 . For example, if there is a attribute “shape”, and the value of “shape” belongs to {triangle, round, rectangle}, then attribute “shape” can convert to three attributes, namely “triangle”, “round” and “rectangle”, and the value of every attributes belongs to
. For example, if there is a attribute “shape”, and the value of “shape” belongs to {triangle, round, rectangle}, then attribute “shape” can convert to three attributes, namely “triangle”, “round” and “rectangle”, and the value of every attributes belongs to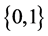 .
.
Definition 3: Let 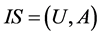 be an information system, if the value of an attribute
be an information system, if the value of an attribute 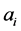 belongs to a set
belongs to a set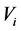 , and the size of
, and the size of 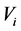 is
is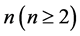 , then convert
, then convert 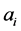 to a series of attributes
to a series of attributes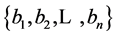 , and call
, and call 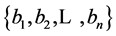 are derived attributes of
are derived attributes of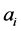 . After carrying out this converting process, attributes set
. After carrying out this converting process, attributes set 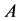 convert to a new attributes set
convert to a new attributes set![]() , then
, then ![]() is called the derived attributes of
is called the derived attributes of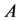 .
.
Definition 4: Let 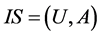 be an information system, assume
be an information system, assume![]() ,
, ![]() is the derived attributes of
is the derived attributes of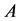 ,
, 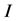 is the relation between
is the relation between ![]() and
and![]() , the we call
, the we call 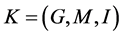 is the single value formal context derived from information system
is the single value formal context derived from information system![]() .
.
3.2. Realization of Approximation Based on Concept Lattice
For the sake of narrative convenience, we agree several symbols in this paper. 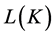 denotes Concept lattice of formal context
denotes Concept lattice of formal context ![]() and
and 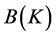 denotes all concepts of
denotes all concepts of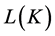 . Lower case letters represents concepts, for example, we use letter
. Lower case letters represents concepts, for example, we use letter ![]() denote a concept, and let
denote a concept, and let 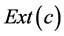 and
and 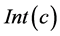 represent extension and intension of concept
represent extension and intension of concept ![]() respectively.
respectively.
Definition 5: Let 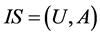 be an information system,
be an information system, 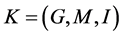 is the single value formal context derived from information system
is the single value formal context derived from information system![]() , assume
, assume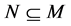 ,
,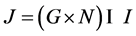 , we call formal context
, we call formal context 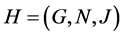 is sub-context of
is sub-context of ![]() regarding
regarding![]() .
.
Theorem 1: Let 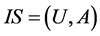 be an information system,
be an information system, 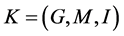 is the single value formal context derived from information system
is the single value formal context derived from information system![]() ,
, 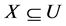 ,
, 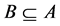 ,
, 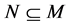 , attribute
, attribute 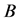 is derived from attribute
is derived from attribute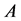 ,
, 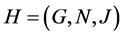 is sub-context of
is sub-context of ![]() regarding
regarding![]() ,
, 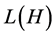 is the concept lattice of
is the concept lattice of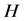 , Upper Approximation:
, Upper Approximation:
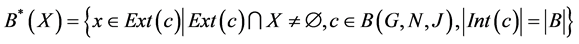 Lower Approximation:
Lower Approximation:
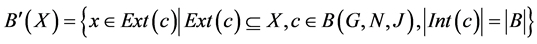 .
.
Proof: According to the definition of concept in FCA, extent set 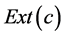 has attributes
has attributes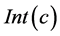 , and size of
, and size of
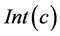 equals to the size of
equals to the size of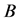 , then
, then 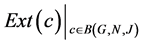 forms the equivalence classes of the B-indiscernibility relation, which means
forms the equivalence classes of the B-indiscernibility relation, which means 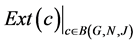 equals to
equals to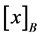 . According to definition of upper and lower approximation, this theorem obviously holds.
. According to definition of upper and lower approximation, this theorem obviously holds.
Theorem 2: Let 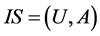 be an information system,
be an information system, 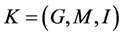 is the single value formal context derived from information system
is the single value formal context derived from information system![]() , assume
, assume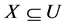 ,
, 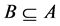 ,
, 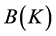 contains all the concepts in concept lattice
contains all the concepts in concept lattice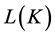 , Upper Approximation is:
, Upper Approximation is:
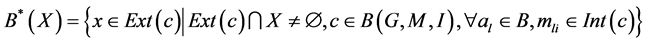 Lower Approximation is:
Lower Approximation is:
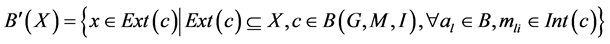 .
.
Proof: According to the definition of concept in FCA, extent set 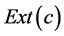 has attributes
has attributes , and
, and
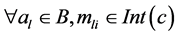 , then
, then 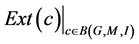 forms the equivalence classes of the B-indiscernibility relation, which means
forms the equivalence classes of the B-indiscernibility relation, which means 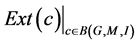 equals to
equals to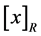 . According to definition upper and lower approximation, this theorem obviously holds.
. According to definition upper and lower approximation, this theorem obviously holds.
3.3. An Example
In an information system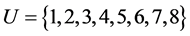 , three are equivalent classes, namely
, three are equivalent classes, namely
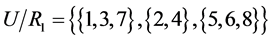 ,
,
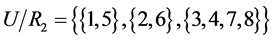 and
and
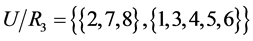 .
.
Let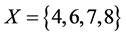 ,
,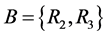 . Now let’s compute
. Now let’s compute 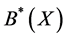 and
and 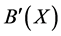 by using Theorem 1 and Theorem 2.
by using Theorem 1 and Theorem 2.
In the above information system, 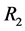 and
and 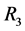 divide
divide ![]() into three equivalent classes, thus the size of the value range of
into three equivalent classes, thus the size of the value range of 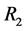 and
and 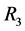 is 3, and then we must convert these two attributes form multiple value to single value. The derived single value context is shown in Table1 By using Godin algorithm [9] , we can build the concept lattice of a given single valued formal context.
is 3, and then we must convert these two attributes form multiple value to single value. The derived single value context is shown in Table1 By using Godin algorithm [9] , we can build the concept lattice of a given single valued formal context.
1) Compute 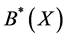 and
and 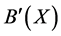 by using Theorem 1 Under the attributes constraint
by using Theorem 1 Under the attributes constraint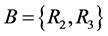 , we get sub-context
, we get sub-context 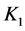 of formal context
of formal context![]() , which includes the columns labeled by
, which includes the columns labeled by 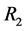 and
and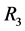 . Concept lattice
. Concept lattice 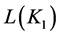 is shown in Figure 1.
is shown in Figure 1.

Figure 1. Concept lattice L (K1).
In concept lattice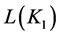 , the concepts whose extent satisfy the constraint
, the concepts whose extent satisfy the constraint 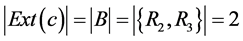 are
are
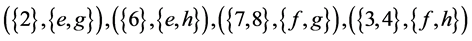 , and
, and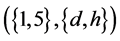 . According Theorem 1, we have
. According Theorem 1, we have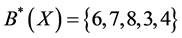 ,
, 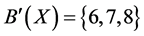 , and
, and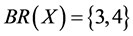 .
.
2) Compute 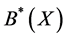 and
and 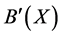 by using Theorem 2 First
by using Theorem 2 First 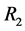 convert to single vale set
convert to single vale set 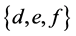 and
and 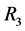 convert to single vale set
convert to single vale set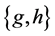 . Besides
. Besides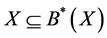 , for the father concept
, for the father concept 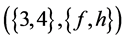 of concept
of concept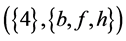 , the intent satisfy
, the intent satisfy 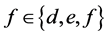 and
and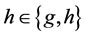 , according to Theorem 2, objects 3 and 4 belongs to
, according to Theorem 2, objects 3 and 4 belongs to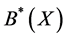 .
.
Finally, we get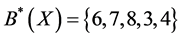 ,
, 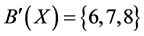 and
and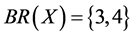 .
.
By using different theory, we get the same result, and to some extent this proves the correctness of our method.
4. Conclusions
There is an intimate link between rough set theory and concept lattice, so rough set approximation operation can be realized being aided by FCA. From this perspective, realizing rough set operation aided by FCA can be seen as a kind of generalization of the concept lattice queries that meet certain conditions.
Realization of rough set approximation operation on concept lattice can be divided into two steps: first, convert multiple value information system to multiple value formal context, and then covert multiple value formal context to single value formal context; second, realize rough set approximation operation aided by formal concept analysis on concept lattice.
The method is expected to be of further use for calculating approximation of rough set that with real values, interval numbers and other self-defined types.
Acknowledgements
The work presented in this paper is supported by National Science Foundation of China (60975033) and Doctorial Foundation of Henan Polytechnic University (B2011-102).
References
- Pawlak, Z. (1991) Rough Sets—Theoretical Aspects of Reasoning about Data. Kluwer Academic, Dordrecht.
- Ganter, B. and Wille, R. (l999) Formal Concept Analysis: Mathematical Foundation. Springer-Verlag, New York.
- Kent, R.E. (1994) Rough Concept Analysis. In: Ziarko, W.P., Ed., Rough Sets and Fuzzy Sets Knowledge Discovery, Springer-Verlag, London, 248-255. http://dx.doi.org/10.1007/978-1-4471-3238-7_30
- Yao, Y.Y. (2004) Concept Lattices in Rough Set Theory. In: Dick, S., Kurgan, L., Pedrycz, W. and Reformat, M., Eds., Proceedings of the 2004 Annual Meeting of the Noah American Fuzzy Information Processing Society, Banff, 27-30 June 2004, 796-801.
- Qu, K.S., Zhai, Y.H., Liang, J.Y., et al. (2007) Representation and Extension of Rough Set Theory Based on Formal Concept Analysis. Journal of Software, 18, 2174-2182. http://dx.doi.org/10.1360/jos182174
- Pawlak, Z. (1998) Granularity of Knowledge, Indiscernibility and Rough Sets. The 1998 IEEE International Conference on Fuzzy Systems Proceedings—IEEE World Congress on Computational Intelligence, Anchorage, 4-9 May 1998, 106-110.
- Wu, C., Yue, Y., Li, M., et al. (2004) The Rough Set Theory and Applications. Engineering Computations, 21, 488-511. http://dx.doi.org/10.1108/02644400410545092
- Scaife, M. and Rogers, Y. (1996) External Cognition: How Do Graphical Representations Work. International Journal of Human Computer Studies, 45, 185-213.
- Godin, R., Missaoui, R. and Alaoui, H. (1995) Incremental Concept Formation Algorithms Based on Galois (coNcept) Lattices. Computational Intelligence, 11, 246-267. http://dx.doi.org/10.1111/j.1467-8640.1995.tb00031.x


