Open Journal of Soil Science
Vol.04 No.07(2014), Article ID:47682,10 pages
10.4236/ojss.2014.47024
Prediction of Soil Fractions (Sand, Silt and Clay) in Surface Layer Based on Natural Radionuclides Concentration in the Soil Using Adaptive Neuro Fuzzy Inference System
Saad Al-Hamed1, Mohamed Wahby1, Mohamed Al-Sulaiman2, Abdulwahed Aboukarima2,3
1Department of Agricultural Engineering, College of Food and Agriculture Sciences, King Saud University, Riyadh, KSA
2Community College, Huraimla, Shaqra University, Huraimla, KSA
3Agricultural Engineering Research Institute, Agricultural Research Centre, Cairo, Egypt
Email: alhamed@ksu.edu.sa, wahby@ksu.edu.sa, mohazizsu@su.edu.sa, aboukarima@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2014; revised 26 June 2014; accepted 3 July 2014
ABSTRACT
In this research, a gamma ray sensor (The Mole) was used to get the natural radionuclides concentration in situ in the surface layer of cultivated soils. For sand, silt and clay predictions, an adaptive neuro fuzzy inference system (ANFIS) was performed to predict such fractions (Sugeno model). The inputs to the system were Potassium (40K), Uranium (238U), Thorium (232Th) and Cesium (137Cs) concentrations. It is concluded that ANFIS structure is acceptable in the prediction of sand, silt and clay considering the studied inputs. Test results and predicted outcomes were compared and acceptable correlations were obtained.
Keywords:
Agriculture, ANFIS, Soil Texture, Natural Radionuclides

1. Introduction
Soil texture refers to the percentage by weight of sand (particles between 0.05 to 2.0 mm), silt (0.002 to 0.05 mm), and clay (<0.002 mm) in a soil sample. It is based on that part of a field dried soil sample that passes through a 2-mm sieve. Soil texture is also classified by a soil’s particle size fractions (sand, silt and clay) [1] .
The quantitative method for determining soil texture is by using special soil sieves with meshes of different grades. It is found that direct measurement of soil texture components is time consuming and relatively expensive. In the conventional procedure, a pre-weighed sample of dried soil is put on top of a column of the sieves and shaken for 30 minutes. The soil collected in each progressively smaller mesh sieve is carefully collected and weighed, and distributions of the various size soil particles can calculated as a percent of the total weight of the sample. Another quantitative method for determining soil texture uses special hydrometers that measure the density of a suspended soil solution over time as the soil particles settle. Indirect methods for determining soil texture are used as an alternative solution. They are based on developing predictive equations for the fraction of sand, silt, and/or clay at the soil surface. They can be achieved with varying levels of success reflectance measurements over tilled fields [2] [3] or by using visible and near infrared spectroscopy [4] .
Soil texture influences the suitability of the soil as a medium for rooting [5] . Clay content is an important factor for soil fertility, as it affects the structural and hydrological properties as well as the nutrient availability. High resolution maps of clay content are therefore a requirement for some precision agriculture applications [6] . Precise determination of the values of soil fractions (sand, silt and clay) is a major concern and an essential criterion in the prediction of drafts of tillage implements [7] . Soil particle size distribution could be used through empirical equations as a means for prediction of soil permeability [8] .
The laboratory or field determination of sand, silt and clay is often very difficult, expensive and requires devices. Therefore mathematical modeling techniques must be suggested for determination of such fractions. In the research conducted by van Egmond et al. [9] , clay content could be predicted by the help of 232Th. On the other hand, soft computing techniques are widely applied to soil science. One of them is fuzzy logic which is particularly attractive due to its ability to solve problems in the absence of accurate mathematical models [10] . It is a powerful concept for handling nonlinear, time varying, and adaptive systems. It permits the use of linguistic values of variables and imprecise relationships for modeling system behavior [11] . In fuzzy inference system, there are different steps (Figure 1) [12] . Lately, fuzzy inference systems were employed as alternate statistical tool for developing of the predictive models to estimate the needed parameters and they have been successfully applied to solve different problems in soil applications [13] . Aali et al. [14] used an adaptive neural-based fuzzy inference system (ANFIS) for estimation of saturation percentage of soils collected from Boukan region in the north-western part of Iran. Percent clay, silt, sand and organic carbon were used as inputs. The results showed that ANFIS model can be used for reasonable estimation of saturation percentage values of soils. Bektas and Ozgan [15] developed a model using ANFIS technique to predict the particle diameter of soil for different cases without the need for a test. The quantities of the sodium hexametaphosphate and the hydrometer reading times were used as inputs in the model. Test results and predicted outcomes were compared and high correlations were obtained. Sezer et al. [8] employed an ANFIS to predict sand permeability. In comparison with nonlinear multiple regression analyses results, it was revealed that ANFIS structure was comparatively successful in the prediction of the permeability utilizing particle shape and grain size distribution information.
The measurement of the natural radionuclides concentration in a soil can be influenced by the fractions of the grain size of the soil [16] . Thus, this study explores the potential of Adaptive Neuro Fuzzy Inference System
Figure 1. General structure of the ANFIS.
(ANFIS) in the prediction of sand, silt and clay values of soils. The data from field experiments conducted in this study were used for training and testing of the ANFIS. The inputs were natural radionuclides concentration in the surface layer of cultivated soils at different regions in Saudi Arabia. They were of 40K, 238U, 232Th and 137Cs.
2. Materials and Methods
2.1. Site of Experiments and Procedures
Natural radionuclides concentrations using gamma-ray spectrometer (The Mole) in situ were investigated to correlate them with soil fractions. The measurements of natural radionuclides concentration, in the surface layer of seven regions, in Saudi Arabia were achieved. These regions include: Al-Kharj, Al-Qassim, Wadi Aldawaser, Hail, Aljouf, Tabuk and Riyadh. Different soil surfaces were scanned by the Mole in each region. The length of the scanned area was about 100 m and the width was about 1 m. The distance between the detector and the soil surface was about 1 m. Ten samples were taken for soil particles analysis form each region. Soil particles analysis determined in laboratory according to standard methods. Table 1 shows some values of the collected data from the studied regions. However, averages of soil moisture content and soil bulk density for the studied regions are found in previous study [17] .
Table 1. Some values of the collected data from the studied regions.
The Mole is consisted of a detector, GPS and laptop and calibrated based on measurements of natural gamma radiation in a field [9] . The gamma radiation detector utilizes a 70 × 150 mm CsI crystal (cesium iodide) coupled to a photomultiplier unit. Gamman software is provided with the Mole system for post processing of the obtained data. During measurements, the Mole detector, GPS and laptop are placed on a fabricated iron carriage unit (Figure 2). The Mole can scan soil surface layer in a few seconds to get different radionuclides properties like 40K, 238U, 232Th and 137Cs.
2.2. Adaptive Neuro Fuzzy Inference System (ANFIS)
ANFIS is a fuzzy mapping algorithm that is based on Tagaki-Sugeno-Kang (TSK) fuzzy inference system [18] . ANFIS is an integration of neural networks and fuzzy logic and have the potential to capture the benefits of both in a single framework. ANFIS utilizes linguistic information from the fuzzy logic as well learning capability of an ANN for automatic fuzzy if-then rule generation and parameter optimization [19] .
A conceptual ANFIS consists of five components: inputs and output database, a Fuzzy system generator, a Fuzzy Inference System (FIS), and an Adaptive Neural Network. The Sugeno-type Fuzzy Inference System [20] which is a combination of a FIS and an Adaptive Neural Network was used in this study for sand, silt and clay modeling. The optimization method utilized was hybrid learning algorithms. For a first-order Sugeno model, a common rule set with two fuzzy if-then rules is as follows:
Rule 1: If x1 is A1 and x2 is B1, then f1 = a1x1 + b1x2 + q1
Rule 2: If x1 is A2 and x2 is B2, then f2 = a2x1 + b2x2 + q2
where, x1 and x2 are the crisp inputs to the node and A1, B1, A2, B2 are fuzzy sets, ai, bi and qi(i = 1, 2) are the coefficients of the first-order polynomial linear functions. Structure of a two-input first-order Sugeno fuzzy model with two rules is shown in Figure 3 and consists of five layers [21] . The five layers of ANFIS model are as follows:
Layer1: (Input nodes): Each node output in this layer is fuzzified by membership grade of a fuzzy set corresponding to each input.
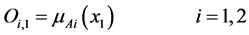 (1)
(1)
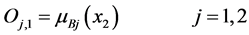 (2)
(2)
where, x1 and x2 are the inputs to node i (i = 1, 2 for x1 and j = 1, 2 for x2) and x1 (or x2) is the input to the ith node and Ai (or Bj) is a fuzzy label.
Layer 2: (Rule nodes): Each node output in this layer represents the firing strength of a rule, which performs fuzzy, AND operation. Each node in this layer, labeled Π, is a stable node which multiplies incoming signals and sends the product out.
Figure 2. A fabricated iron carriage.
Figure 3. ANFIS architecture.
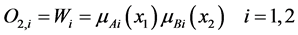 (3)
(3)
Layer 3: (Average nodes): In this layer, the nodes calculate the ratio of the ith rules firing strength to the sum of all rules firing strengths
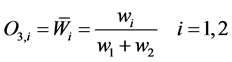 (4)
(4)
Layer 4: (Consequent nodes): In this layer, the contribution of ith rules towards the total output or the model output and/or the function calculated as follows:
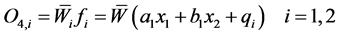 (5)
(5)
where 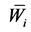 the output of layer 3 and ai, bi, qi are the coefficients of linear combination in Sugeno inference system. These parameters of this layer are referred to as consequent parameters.
the output of layer 3 and ai, bi, qi are the coefficients of linear combination in Sugeno inference system. These parameters of this layer are referred to as consequent parameters.
Layer 5: (Output nodes): The node output in this layer is the overall output of the system, which is the summation of all coming signals
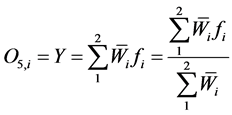 (6)
(6)
ANFIS requires a training data set of desired input/output pair (x1, x2···xm , Y) depicting the target system to be modeled. ANFIS adaptively maps the inputs (x1, x2···xm) to the outputs (Y) through Membership Functions (MFs), the rule base and the related parameters emulating the given training data set. It starts with initial MFs, in terms of type and number, and the rule base that can be designed intuitively. In this study, the training process continues till the desired number of training steps (epochs) is achieved. Detailed information of ANFIS can be found in Jang [21] .
2.3. ANFIS Model Development
There are no fixed rules for developing an ANFIS model [22] . In current study, the 40K, 238U, 232Th and 137Cs which were measured in-situ were used as inputs and sand, silt and clay contents were used as outputs. The data in ANFIS are usually divided into two sets: training set and testing set. The training data are used for the training of ANFIS, while the testing data are used to evaluate the model performance. In this study (total of 31 observations) were divided into two data sets. The first data set containing 25 patterns of the records was used as the training data; the second data set containing 6 patterns of the records was applied as the testing data.
ANFIS model developed in this study using MATLAB toolbox (MATLAB 7.11.0.584 (R2010b)) has four inputs (40K, 238U, 232Th and 137Cs) and three outputs. Different MFs available in MATLAB toolbox and numbers were tested (data not included) and 5 “trimf” (triangle) MFs were elected for each input due to their small training error compared with other MFs. The numerical range was used for 40K (103.2 - 644.5 Bq/kg), for 238U (12.88 - 77.84 Bq/kg), for 232Th (10.42 - 113.2 Bq/kg) and for 137Cs (3.03 - 23.63 Bq/kg). The numerical range was used for sand (63.6% - 88.9%), for silt (7.2% - 20.1%) and for clay (3.0% - 21.0%).
In the training of the model, a “hybrid learning algorithm” was used and the number of epochs was chosen as 3. The number of the MFs is 5 for each input with five linguistic terms {very low, low, medium, high, very high} and the total rules were 625 (5 × 5 × 5 × 5). The number of nodes was 1297, of linear parameters was 3125, and of nonlinear parameters were 60. The total number of parameters was 3185 in the model. The error of the model was 0.00057268 for clay and the type of the membership function was “trimf”, output membership function is linear. For sand ANFIS model, the error was 0.000207015 and for silt ANFIS model, the error was 0.000378577.
2.4. Evaluation the Models
After building and training the ANFIS models, in order to evaluate the accuracy of them, the predicted results were compared with experimental data. In fact, the coefficient of determination (R2) between the measured and predicted values is a good indicator to check the prediction performance of the model [23] . The performance of a model is also examined using some main statistical measures that are well known in literature such as root mean square error (RMSE), mean absolute deviation (MAD) [24] . Mean absolute deviation is used for measuring of mean absolute deviation of the measured values from the predicted values. It has a unit. It is expressed as,
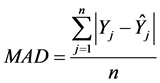 (7)
(7)
where, Y and 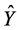 are the measured and predicted values respectively and n is the number of observations. RMSE yields the residual error in terms of the mean square error expressed as,
are the measured and predicted values respectively and n is the number of observations. RMSE yields the residual error in terms of the mean square error expressed as,
 (8)
(8)
3. Results and Discussion
3.1. Distribution of Natural Radionuclides in the Surface Soil
The estimation of sand, silt and clay contents in a soil is highly important for soil and agricultural engineering researches; in particular for the determination of draft requirements in specified soil. As a result of this study, the variation of concentration of soil natural radionuclides namely, Potassium (40K), Uranium (238U), Thorium (232Th) and Cesium (137Cs) with the quantity of sand, silt and clay in a soil were investigated through experimental work. Figures 4-6 illustrate the relationship among sand, silt and clay contents and 40K, 238U, 232Th and 137Cs concentrations, respectively. The obtained values of activity concentration are in good agreement with the recommended values for background gamma radiation reported for soils worldwide [25] : 16 - 110 for 238U, 16 - 64 for 232Th, and 140 - 850 for 40K.
The levels of detected radionuclides in soil surface layer in this research indicated variations among regions and this may be attributed to the diversity of formations and textures of the soil in the studied regions as reported by Saleh [26] . The same findings was observed by Thabayneh and Jazzar [27] who attributed the differences between the activity concentration of 238U, 232Th, 40K and 137Cs to soil type.
It is clear that increasing concentration of 40K, 238U, 232Th and 137Cs in soil surface layer results to decrease sand content in the soil, as illustrated in Figure 4. This is may be attributed to the fact of sand fraction enhances
Figure 4. Relationship between sand content and 40K, 238U, 232Th and 137Cs concentrations.
due to larger pores the vertical mobility of radionuclides in the soil as reported by Golmakani et al. [28] and Blanco Rodriguez et al. [29] . However, Vukasinovic et al. [30] also found the soil profile with the highest average radionuclide activity concentration contained the lowest sand percentage. This finding was also observed by Al-Sulaiti [31] who indicated that the finest soil grain size had the highest activity concentration of 40K. Also, the variability of 40K among regions could be due to the differences in land management, for example, fertilization, plowing practices, geology and geography [32] .
It is noted that increasing concentration of 40K, 238U, 232Th and 137Cs in soil surface layer results to increase silt and clay contents in the soil, as illustrated in Figure 5 and Figure 6, respectively. This finding is agreement with Vukasinovic et al. [30] who found the soil profile with the highest average radionuclide activity concentration contained the highest amount of clay. Higher radionuclide activity was found in the soil had high clay content [33] . According to previous study [34] the reason for high radionuclides activity in clays is due to the fact that clay minerals are mainly composed by aluminum silicates and they are characterized by small sized grain and negative charged surface. In this way clay particles easily absorb cations on their surface. Also, a radionuclide is adsorbed onto clay surfaces [35] which could be increased it with clay content.
3.2. Performance of the ANFIS Models
To estimate the quantity of sand, silt and clay in a soil, an ANFIS model was developed. It uses 40K, 238U, 232Th and 137Cs concentrations as inputs. The experimental results and the results of the ANFIS method were compared. It was seen that the sand, silt and clay contents in the soil have various values depending on the quantity of natural radionuclides concentration. The relationships between experimental results and ANFIS model exhibited a good correlation for test set. The coefficients of determination were found to be R2 = 0.852 for the testing
Figure 5. Relationship between silt content and 40K, 238U, 232Th and 137Cs concentration.
data set with ANFIS model of sand prediction, R2 = 0.7631 for the testing data set with ANFIS model of slit prediction and R2 = 0.7788 for the testing data set with ANFIS model of clay prediction. Based on the results of the study, it could be said that the ANFIS method can be used for modeling of the sand, silt and clay of the soil according to the 40K, 238U, 232Th and 137Cs concentrations in the soil. The experimental and ANFIS results and correlations of sand, silt and clay are given in Figure 7 for testing data set. The errors criteria which indicate the performance of the ANFIS model using testing data set is shown in Table 2. Based on the values of Table 2, satisfactory performance is seen owing to the lower RMSE and MAD values. For test data set, the RMSE and MAD values have been obtained 14.047%, 4.483 % for sand, respectively. These values for silt were 3.727% and 1.55% and for clay they were 3.266% and 1.05%, respectively. The obtained results show that ANFIS model with 40K, 238U, 232Th and 137Cs concentrations inputs have a weight on prediction of sand, silt and clay percentage of a soil.
4. Conclusion
In this study Adaptive Neural-based Fuzzy Inference System (ANFIS) was used for prediction of sand, silt and clay content in a soil using natural radionuclides concentration in it namely, Potassium (40K), Uranium (238U), Thorium (232Th) and Cesium (137Cs). The results showed that constructed ANFIS was effectively able to predict sand, silt and clay contents. The prediction accuracy of the model was fairly good (predictive ability and for the coefficient of correlation) based on the results of the testing data performance, and the calculated coefficient of correlation of training and testing data.
Figure 6. Relationship between clay content and 40K, 238U, 232Th and 137Cs concentrations.
Figure 7. The experimental and ANFIS results and correlations for testing data set of sand, silt and clay.
Table 2. The errors criteria which indicate the performance of the ANFIS model using testing data set.
Acknowledgements
Authors express their gratitude to the National Plan for Science, Technology and Innovation Program, King Saud University, Saudi Arabia for financially supporting this research effort as a part of the project entitled “Modeling of energy consumption during seed bed preparation operation based on soil mechanical properties”, No. 09-SPA876-02.
References
- Dinnes, D.L. (2004) Assessments of Practices to Reduce Nitrogen and Phosphorus Nonpoint Source Pollution of Iowa’s Surface Waters. Iowa Department of Natural Resources in Cooperation with the USDA-ARS National Soil Tilth Laboratory Iowa, USA, 380p.
- Suliman, A.S. and Post, D.F. (1988) Relationship between Soil Spectral Properties and Sand, Silt, and Clay Content of the Soils on the University of Arizona Maricopa Agricultural Centre. Proceedings of Hydrology and Water Resources in Arizona and the Southwest, 16 April 1988, Tucson, Arizona (Arizona-Nevada Academy of Science, Tucson Arizona), 18, 61-65.
- Coleman, T.L., Agbu, P.A., Montgomery, O.L., Gao, T. and Prasad, S. (1991) Spectral Band Selection for Quantifying Selected Properties in Highly Weathered Soils. Soil Science, 151, 355-361. http://dx.doi.org/10.1097/00010694-199105000-00005
- Stenberg, B., Raphael, A., Rossel, V., Mouazen, A. and Wetterlind, J. (2010) Visible and Near Infrared Spectroscopy in Soil Science. In: Sparks, D.L., Ed., Advances in Agronomy, Academic Press, Burlington, 163-215.
- Barnes, E.M., Sudduth, K.A., Hummel, J.W., Lesch, S.M., Corwinm, D.L., Yang, C., Daughtry, C.S.T. and Bausch, W.C. (2003) Remote- and Ground-Based Sensor Techniques to Map Soil Properties. Photogrammetric Engineering & Remote Sensing, 69, 619-630.http://dx.doi.org/10.14358/PERS.69.6.619
- Piikki, K., Soderstrom, M. and Stenberg, B. (2011) Sensor Data Fusion for Topsoil Clay Mapping of an Agricultural Field. The Second Global Workshop on Proximal Soil Sensing, Montreal, 15-18 May 2011, 56-59.
- Aboukarima, A.M. and Saad, A.F. (2006) Assessment of Different Indices Depicting Soil Texture for Predicting Chisel Plow Draft Using Neural Networks. Alexandria Science Exchange Journal, 27, 170-180.
- Sezer, A., Goktepe, B.A. and Altun, S. (2010) Adaptive Neuro-Fuzzy Approach for Sand Permeability Estimation. Environmental Engineering and Management Journal, 9, 231-238.
- Van Egmond, F.M., Loonstra, E.H and Limburg, J. (2008) Gamma-Ray Sensor for Topsoil Mapping: The Mole. Proceedings of the 1st Workshop in High-Resolution Digital Soil Sensing and Mapping, Sydney, 5-8 February 2008, Workshop Program and Papers, Volume II.
- Samhouri, S.M. and Surgenor, B.W. (2005) Surface Roughness in Grinding: On-Line Prediction with Adaptive Neuro- Fuzzy Inference System. Transactions of NAMRI/SME, 33, 57-64.
- Hosseinzadeh, B., Zareiforoush, H., Adabi, M.E. and Motevali, A. (2011) Development of a Fuzzy Model to Determine the Optimum Shear Strength of Wheat Stem. International Journal of Computer Science and Telecommunications, 2, 56-60.
- Tinkir, M. (2011) A New Approach for Interval Type-2 by Using Adaptive Network Based Fuzzy Inference System. International Journal of Physical Sciences, 6, 4502-4518.
- Mcbratney, A.B. and Odeh, I.O.A. (1997) Application of Fuzzy Sets in Soil Science: Fuzzy Logic, Fuzzy Measurements and Fuzzy Decisions. Geoderma, 77, 85-113. http://dx.doi.org/10.1016/S0016-7061(97)00017-7
- Aali, K.A., Parsinejad, M. and Rahmani, B. (2009) Estimation of Saturation Percentage of Soil Using Multiple Regression, ANN and ANFIS Techniques. Computer and Information Science, 2, 127-136.
- Bektas, S. and Ozgan, E. (2010) Adaptive Neuro Fuzzy Inference System for Estimating Particle Diameter of Soils in Micro Structure for Varying Quantities of Sodium Hexametaphosphate. Scientific Research and Essays, 5, 782-789.
- Hebinck, K., Middelkoop, H., Van Diepen, N., Van der Graaf, E.R. and De Meijer, R.J. (2007) Radiometric Fingerprinting of Fluvial Sediments in the Rhine-Meuse Delta, the Netherlands—A Feasibility Test. Netherlands Journal of Geosciences, 86, 229-240.
- Al-Hamed, S., Wahby, M., Al-Sulaiman, M., Al-Saqer, S. and Aboukarima, A. (2012) Application of Artificial Neural Networks to Predict Natural Soil Radionuclides Concentrations in Some Saudi Agricultural Soils. Archives Des Sciences, 65, 196-206.
- Jang, J.S.R, Sun, C.T. and Mizutani, E. (1997) Neuro-Fuzzy and Soft Computing. Prentice-Hall, Englewood Cliffs.
- Kumar, P., Kumar, D., Jaipaul, A. and Tiwari, K. (2012) Evaporation Estimation Using Artificial Neural Networks and Adaptive Neuro-Fuzzy Inference System Techniques. Pakistan Journal of Meteorology, 8, 81-88.
- Takagi, T. and Sugeno, M. (1985) Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Transactions on Systems, Man and Cybernetics, 15, 116-132. http://dx.doi.org/10.1109/TSMC.1985.6313399
- Jang, J.-S.R. (1993) ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Transactions on Systems, Man and Cybernetics, 23, 665-685. http://dx.doi.org/10.1109/21.256541
- Yan, H., Zou, Z. and Wang, H. (2010) Adaptive Neuro Fuzzy Inference System for Classification of Water Quality Status. Journal of Environmental Sciences, 22, 1891-1896. http://dx.doi.org/10.1016/S1001-0742(09)60335-1
- Gokceoglu, C. and Zorlu, K. (2004) A Fuzzy Model to Predict the Uniaxial Compressive Strength and the Modulus of Elasticity of a Problematic Rock. Engineering Applications of Artificial Intelligence, 17, 61-72. http://dx.doi.org/10.1016/j.engappai.2003.11.006
- Bisht, D.C.S. and Jangid, A. (2011) Discharge Modeling Using Adaptive Neuro-Fuzzy Inference System. International Journal of Advanced Science and Technology, 31, 99-114.
- UNSCEAR (United Nations Science Committee on the Effects of Atomic Radiation) (2000) Report to the General Assembly, with Scientific Annexes, United Nations. New York.
- Saleh, I.H. (2012) Radioactivity of 238U, 232Th, 40K, and 137Cs and Assessment of Depleted Uranium in Soil of the Musandam Peninsula, Sultanate of Oman. Turkish Journal of Engineering and Environmental Sciences, 36, 236-248.
- Thabayneh, K.M. and Jazzar, M.M. (2012) Natural Radioactivity Levels and Estimation of Radiation Exposure in Environmental Soil Samples from Tulkarem Province-Palestine. Open Journal of Soil Science, 2, 7-16. http://dx.doi.org/10.4236/ojss.2012.21002
- Golmakani, S., Moghaddam, M.V. and Hosseini, T. (2008) Factors Affecting the Transfer of Radionuclides from the Environment to Plants. Radiation Protection Dosimetry, 130, 368-375. http://dx.doi.org/10.1093/rpd/ncn063
- Blanco Rodriguez, P., Tome, F.V., Lozano, J.C. and Perez-Fernandez, M.A. (2008) Influence of Soil Texture on the Distribution and Availability of 238U, 230Th, and 226Ra in Soils. Journal of Environmental Radioactivity, 99, 1247- 1254. http://dx.doi.org/10.1016/j.jenvrad.2008.03.004
- Vukasinovic, I., Dordevic, A., Rajkovic, M.B., Todorovic, D. and Pavlovic, V.B. (2010) Distribution of Natural Radionuclides in Anthrosol-Type Soil. Turkish Journal of Agriculture and Forestry, 34, 539-546.
- Al-Sulaiti, H.A. (2011) Determination of Natural Radioactivity Levels in the State of Qatar Using High Resolution Gamma-Ray Spectrometry. PhD Thesis, Department of Physics, Faculty of Engineering and Physical Sciences, University of Surrey, Guildford, Surrey.
- Tchokossa, P., Makon, T.B. and Nemba, R.M. (2012) Assessment of Radioactivity Contents and Associated Risks in Some Soil Used for Agriculture and Building Materials in Cameroon. Journal of Environmental Protection, 3, 1571- 1578. http://dx.doi.org/10.4236/jep.2012.311173
- Pallavicini, N. (2011) Activity Concentration and Transfer Factors of Natural and Artificial Radionuclides in the Swedish Counties of Uppsala and Jämtland. MSc Thesis, Swedish University of Agricultural Sciences, Department of Soil and Environment, Uppsala, 61p.
- El-Arabi, A.M., Abbady, A.G.E. and Hussein, A.S. (2006) Gamma-Ray Measurements of Natural Radioactivity in Sedimentary Rocks from Egypt. Nuclear Science and Technique, 17, 123-128. http://dx.doi.org/10.1016/S1001-8042(06)60024-9
- Navas, A., Soto, J. and Machin, J. (2002) Edaphic and Physiographic Factors Affecting the Distribution of Natural Gamma-Emitting Radionuclides in the Soils of the Arnas Catchment in the Central Spanish Pyrenees. European Journal of Soil Science, 53, 629-638. http://dx.doi.org/10.1046/j.1365-2389.2002.00488.x




















