Open Journal of Modern Hydrology
Vol.4 No.3(2014), Article ID:47562,13 pages
DOI:10.4236/ojmh.2014.43006
Stochastic Characteristics and Modelling of Monthly Rainfall Time Series of Ilorin, Nigeria
Ahaneku, I. Edwin1, Otache, Y. Martins2*
1Department of Agricultural & Bioresources Engineering, Michael Okpara University of Agriculture, Umudike, Nigeria
2Department of Agricultural & Bioresources Engineering, Federal University of Technology, Minna, Nigeria
Email: *drotachemartyns@gmail.com, *martynso_pm@futminna.edu.ng
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 April 2014; revised 27 May 2014; accepted 26 June 2014
ABSTRACT
The analysis of time series is essential for building mathematical models to generate synthetic hydrologic records, to forecast hydrologic events, to detect intrinsic stochastic characteristics of hydrologic variables as well to fill missing and extend records. To this end, this paper examined the stochastic characteristics of the monthly rainfall series of Ilorin, Nigeria vis-à-vis modelling of same using four modelling schemes. The Decomposition, Square root transformation-deseasonalisation, Composite, and Periodic Autoregressive (T-F) modelling schemes were adopted. Results of basic analysis of the stochastic characteristics revealed that the monthly series does not show any discernible presence of long-term trend, though there is a seeming inter-decadal annual variation. The series exhibits strong seasonality throughout its length, both in the moments and autocorrelation and significantly intermittent. Based on assessment of the respective models, the performance of the different modelling schemes can be expressed in this order: T-F > Composite > Square root transformation-Deseasonalised > Decomposition. Considering the results obtained, modelling of monthly rainfall series in the presence of serial correlation between months should be based on the establishment of conditional probability framework. On the other hand, in view of the inadequacy of these modelling schemes, because of the autoregressive model components in the coupling protocol, nonlinear deterministic methods such as Artificial Neural Network, Wavelet models could be viable complements to the linear stochastic framework.
Keywords:Stochastic, Time Series, Modelling, Rainfall, Periodicity, Ergodic, Ilorin

1. Introduction
The assessment of the dynamics and regime of a particular hydrologic phenomenon is imperative; especially the time-based characteristics. Time-based characteristics of hydrological data are of great significance in the planning, designing and operation of water systems. This significance is informed more largely due to the variability and oscillatory behaviour of hydrological sequences. Against this backdrop therefore, as noted by Kottegoda [1] , the lack of complete understanding of the physical processes involved and the consequent uncertainties in the magnitudes and frequencies of future events highlight the importance of time series analysis. Thus, the main objective of any time series analysis is to understand the mechanism that generates the data and also, but not necessarily, to produce likely future sequences over a short period of time. This is usually not without taking cognisance of the appurtenant uncertainty resulting from spatio-temporal variability of hydrologic processes. This fact becomes increasingly important considering that rainfall is a complex atmospheric process, which is space and time dependent and basically not easily predictable [2] .
Like any other aspect of science and engineering developments, there has been a tremendous introduction of new concepts and ideas in rainfall cum precipitation study in general. Notable of such are researches in various directions including space-time structure and variability of rainfall. In this regard, there has been a significant shift from point process models to models based on concepts of scale invariance [3] . This is so because point process models suffer from the inability to describe the statistical structure of rainfall over a wide range of scales as well as from difficulty in parameter estimation; whereas scaling models provide parsimonious representations over a wide range of scales. These are supported by theoretical arguments and empirical evidence that rainfall exhibits a scale-invariant symmetry (e.g., [3] [4] ). In this regard, the trend in scale-invariant rainfall models evolved around multiplicative cascades which have their origin in the statistical theory of turbulence [3] . However, it is important to note that despite the good attributes, the estimation of parameters is not a simple issue [3] . As noted by Holley and Waymire [5] , the independent and identically distributed “bounded generators” give rise to non-ergodic cascades. Recent developments in stochastic rainfall analysis in this direction deal with the introduction of wavelet transforms and importantly, the use of Artificial Neural Network, diffusion model (e.g., [6] ), Markovian type models (e.g., [7] [8] ) and Disaggregation models (e.g., [9] ).
Though generally, hydrologic processes such as precipitation and runoff evolve on a continuous time scale and their estimation correspondingly unduly difficult, in particular, rainfall modelling and its quantitative estimation or forecasting are important considering the fact that it is a critical weather parameter in the estimation of crop water requirement, and development of long lead time flood and flash-flood warning systems. However, it suffices to note that despite substantial progress, several modelling issues still remained unresolved [3] . For instance, “what are the limits of predictability at various temporal and spatial scales” and “the properties of the rainfall field to be preserved by the model”? The modelling of rainfall is motivated by the desire to obtain real-time statistical forecasts of rainfall but as noted by Lovejoy and Schertzer [10] , due to nonlinear interactions that take place at a wide range of scales, several details of the rainfall dynamics are unimportant and too, the resulting fields fall within a universality of multifractals characterised by three parameters. Thus, the objective of this paper like any modelling exercise is to obtain synthetic sequences of rainfall with the same statistical properties as the historical ones. To this end, stochastic characteristics of the rainfall fields like moments (first and second order) and dependence structure shall be analysed while different stochastic models will also be developed for short-term forecasts.
2. Materials and Methods
2.1. Materials
Study Location and Data Assembly
The study location is Ilorin (North central Nigeria) at longitude 4˚35' and latitude 8˚30'. It has elevation of between 273 to 333 m and a mean annual temperature of about 27˚C and is characterised by a distinct bi-seasonal weather pattern; i.e., wet and dry. The wet season starts in April and ends in October, while the dry season starts in November and ends in March. The mean annual rainfall is 1150mm, while the relative humidity ranges from 65% - 80%. Figure 1 shows the map of Nigeria with the study location indicated as inset. For this study, historical rainfall time series of Ilorin was used. To this end, mean monthly rain gauge rainfall values (i.e., point rainfall) for approximately 43 years’ time period (1967-2009) were collected. Preliminary analysis of stochastic
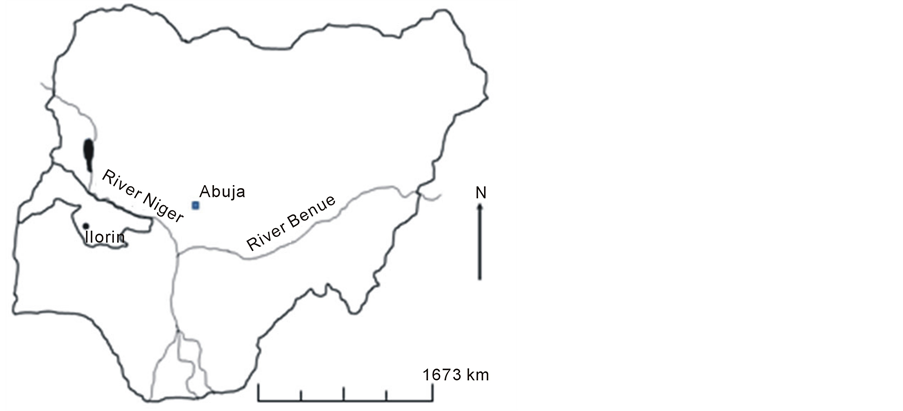
Figure 1. Map of Nigeria showing the study location.
characteristics like moments and dependence structure of the data series was done to be able to evaluate randomness and trend pattern. In this regard, the time series plot was examined to establish whether it does exhibit intermittency or otherwise as well as seasonal characteristics like trend and moments. The objective here is to evaluate seasonality in the moments. Analysis of dependence structure was done in time and frequency domains; basically through autocorrelation and spectral density, respectively.
2.2. Methodology
2.2.1. Modelling Framework
In this study, four (4) different modelling schemes were employed; these are a) decomposition, b) square root transformation-deseasonalisation strategy, c) composite modelling and d) Periodic modelling (Thomas-Fiering).
1) Decomposition strategy Here, the data series was de-trended, deseasonalised and further smoothen with a moving average (MA) of order 6 based on the autocorrelation structure of the original raw data. To this end, an additive model of the form in equation (1) was employed.
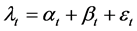 (1)
(1)
where,
 is the rainfall series,
is the rainfall series,
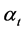 the long-term trend,
the long-term trend,
 the periodic fluctuations and
the periodic fluctuations and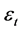 , the stochastic component. The fitted trend
equation is:
, the stochastic component. The fitted trend
equation is:
 (2)
(2)
This procedure requires that the data series be decomposed into seasonal components; the deseasonalisation after the removal of the long-term trend was done by using the seasonal adjustment factors (SAF). These values (SAF) indicate the effect of each period on the level of the series. Table 1 shows the respective seasonal adjustment factors or indices whereas Figure 2 details the entire decomposition process.
After the decomposition process and smoothening, an ARIMA model was fitted into
the random or stochastic component left. Based on the analysis of the autocorrelation
functions of the random component, a multiplicative ARIMA model was fitted; in this
regard,
 was adjudged to be the better candidate model (see Appendix); this derives from the fact that ordinary integrated
moving average scheme may not necessarily account for the non-seasonal autoregressive
behaviour of hydrologic processes [11]
. Figure 3 shows the correlogram of the model residuals.
was adjudged to be the better candidate model (see Appendix); this derives from the fact that ordinary integrated
moving average scheme may not necessarily account for the non-seasonal autoregressive
behaviour of hydrologic processes [11]
. Figure 3 shows the correlogram of the model residuals.
2) Square root transformation-deseasonalisation scheme Based on the suggestion of Delleur and Kavvas [12] , the square root transformation of the data was used to obtain a series which is approximately normally distributed. The series of the monthly rainfall square roots were
 (a)
(a) (b)
(b)
Figure 2. Seasonal analysis of the original mean rainfall series (RF) before (a) and after (b) detrending.
rescaled (deseasonalised) by subtracting from each term of the series by the corresponding seasonal mean and dividing same by the corresponding standard deviation. The deseasonalisation process is according as:
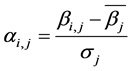 (3a)
(3a)
where,
 is the deseasonalised series,
is the deseasonalised series,
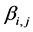 the square root transformed series,
the square root transformed series,
![]() the seasonal means and
the seasonal means and
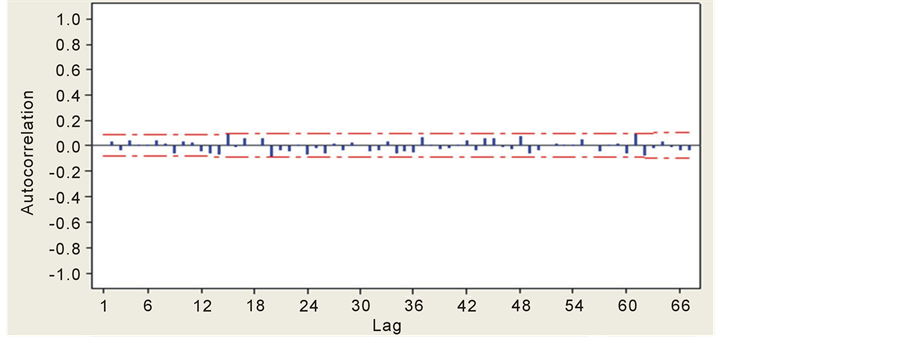
Figure 3. Correlogram of ARIMA (1, 0, 0) × (1, 0, 1)12 model residuals fitted to the stochastic component.
 the seasonal standard deviations.
the seasonal standard deviations.
Using the autocorrelation functions of the square root transformed and deseasonalised
series, a seasonal ARIMA model of the form:
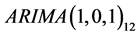 was fitted (as shown in Appendix).
To retrieve the square root transformed series with its seasonal component, a reversed
rescaling procedure was done; that is,
was fitted (as shown in Appendix).
To retrieve the square root transformed series with its seasonal component, a reversed
rescaling procedure was done; that is,
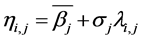 (3b)
(3b)
where, j is the month in a 12-month annual cycle and
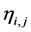 is the forecasted square root transformed periodic monthly rainfall series.
is the forecasted square root transformed periodic monthly rainfall series.
3) Composite modelling The composite modelling entails decomposing the original data series into its various components; i.e., deterministic and a stochastic component which accounts for the random effects (dependent and independent parts) [13] . In this regard, the time series rf(t), was represented by a decomposition model of the additive type according as equation (4).
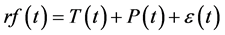 (4)
(4)
where, T(t) is the trend component, P(t) the periodic component and ε(t), the stochastic component.
For the identification of trend, annual rainfall series was used. The annual series was obtained by aggregating the 43 years annual series. In the actual trend detection procedure, a hypothesis of no trend was made and the value of the test statistic (Z) was calculated by using 1) Turning Point Test, 2) Kendall’s Rank Correlation Test and 3) Mann-Kendall Trend Test. The computed values of the test statistic in all instances were −0.852, −0.429, and 0.195, respectively. Considering the values of the computed test statistic (Z), at 5% level of significance, the Z values do not provide reason to suspect the presence of any discernible long-term trend. Thus, the observed rainfall series may be treated as trend free. Hence the composite model, i.e., equation (4) reduces to:
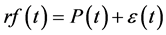 (5)
(5)
To confirm the presence of periodic component in the monthly rainfall series, a correlogram of the series was drawn. Figure 4 shows the periodic, oscillating nature of the time series.
The parameters of the periodic component of the composite model were evaluated by using the classical harmonic analysis method. To this end, the Cumulative Periodogram (CP) approach was adopted. In this case, the point of intersection of the fast increase in the Periodogram (CPi) and the slow increase is considered and the corresponding harmonics taken as significant and the remaining treated as errors and passed on to the random component; i.e., insignificant. From figure 5, the first four harmonics are considered significant. The periodic component can be expressed as in equation (6a).
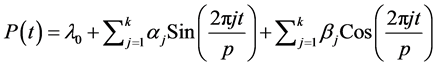 (6a)
(6a)
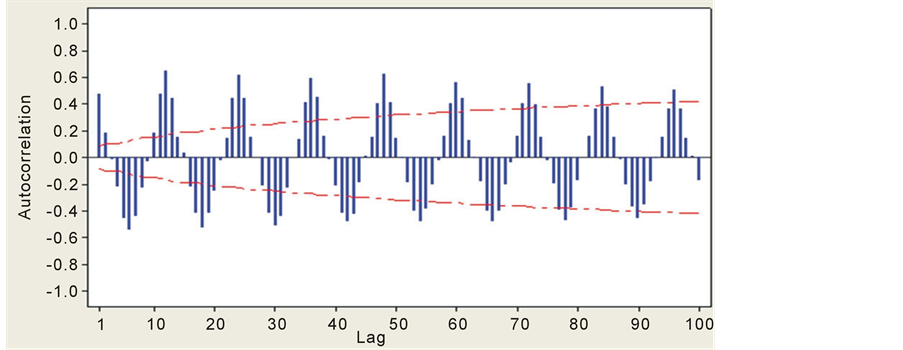
Figure 4. Autocorrelation function of the original rainfall series based on water year regime.
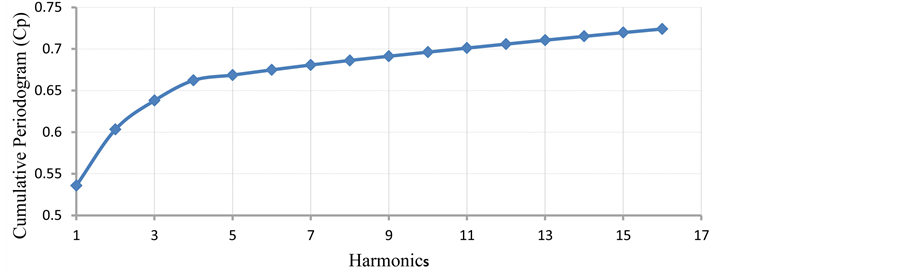
Figure 5. Cumulative periodogram of the mean monthly rainfall series.
where, k is the maximum harmonics,
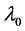 the mean and p, the base period; here, it is equal to 12.
the mean and p, the base period; here, it is equal to 12.
Based on figure 5, the resulting periodic component can be expressed according as equation (6b).
 (6b)
(6b)
Table 2 shows the values of the harmonic coefficients.
The stochastic component (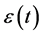 ), was represented by an autoregressive model
of the form:
), was represented by an autoregressive model
of the form:
 (6c)
(6c)
Based on the autocorrelation of the residual series left after the periodic component
was removed from the original series,
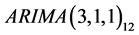 model was fitted to it (see Appendix).
Resulting from this, the final composite model of the monthly rainfall series, i.e.,
equation (5) then becomes
model was fitted to it (see Appendix).
Resulting from this, the final composite model of the monthly rainfall series, i.e.,
equation (5) then becomes
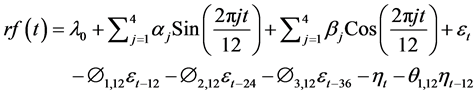 (6d)
(6d)
4) Periodic Autoregressive modelling Scheme Modelling of the monthly rainfall series using periodic autoregressive model was done by adopting the Thomas-Fiering (T-F) model. The T-F model is a linear stochastic model for stimulating synthetic series of seasonal hydrologic process. The schema for the rainfall modelling using this framework takes the form
 (7)
(7)
Table 2. Harmonic coefficients.
This model uses a linear regression relationship to relate the storm rft+1
in the (t+1) month to storm rft in the t(th) month. Here,
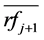 and
and
![]() are seasonal means during months j+1 and j, respectively while bj is
the regression coefficient and
are seasonal means during months j+1 and j, respectively while bj is
the regression coefficient and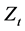 , a normal deviate with zero mean and unit variance.
In the simulation process, negative rainfall values generated were retained and
used to derive subsequent values in the sequence and later replaced by zero when
the generated sequence was completed.
, a normal deviate with zero mean and unit variance.
In the simulation process, negative rainfall values generated were retained and
used to derive subsequent values in the sequence and later replaced by zero when
the generated sequence was completed.
2.2.2. Model Validation and Forecast Functions
In all the instances, for the respective modelling strategy, split sampling procedure was adopted; i.e., one segment of the monthly rainfall series (40 years’ time period) was used for modelling while the remaining three years data was used for model validation. For model validation/forecasting, forecast functions corresponding to the respective ARIMA modelling scheme was adopted using the difference equation form. In this regard, recalling that Zt(L) = [Zt+L], using square brackets to signify conditional expectations and noting that
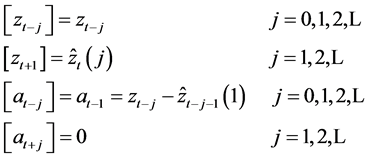 (8)
(8)
the following forecast functions were employed, viz:a) Decomposition modelling scheme:
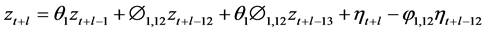
b) Square root transformation-deseasonalisation strategy:
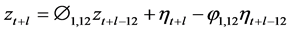
c) Composite modelling scheme (i.e., the stochastic component):
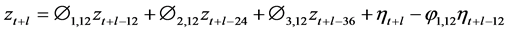
3. Results and Discussion
3.1. Assessment of Stochastic Characteristics and Findings
Hydrologic processes such as precipitation and runoff evolve on a continuous time scale. The implication(s) of this is simple; as shown by Figure 6, the rainfall time series plot exhibits typical characteristic movement with seasonality, cyclical or sinusoidal and random components. This phenomenon translates into statistical characteristics which vary within an annual cycle. Figure 6 shows clearly a discernible seasonal or periodic pattern; it is a periodic-stochastic series since, in addition to the periodic pattern, a random pattern is also evident. In the light of this, it suffices to note that even though, monthly and annual rainfalls are usually non-intermittent, in semiarid and arid regions, monthly and annual precipitation may be intermittent [14] . Also, as noted by Chebaane et al. [14] , this is imperative considering the fact that hydrologic time series are intermittent when the variable under consideration takes on nonzero and zero values throughout the length of record. Interesting too, is the seasonal autocorrelation. Seasonal autocorrelations for monthly precipitation are generally not significantly different from zero; figure 7 attests to this fact. The fall out of this is that the rainfall time series are uncorrelated, depicting strong homogeneity. This phenomenon connotes intermittency of the series, most especially considering
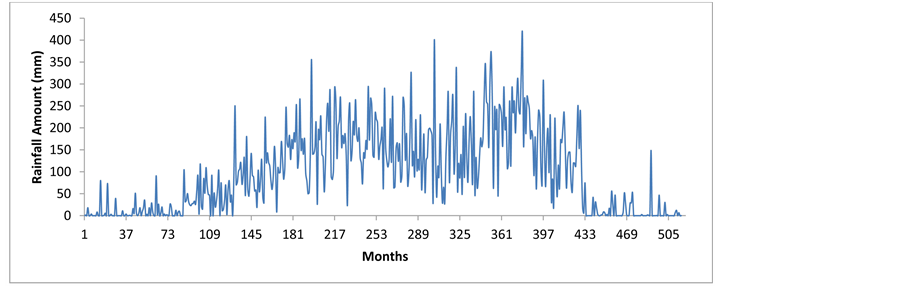
Figure 6. Monthly rainfall time series plot.
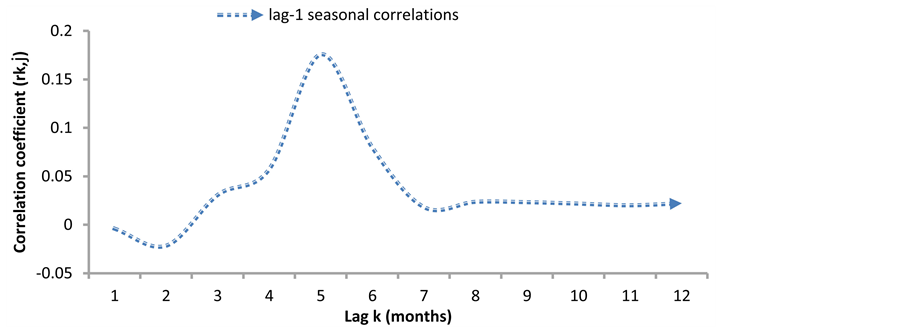
Figure 7. Seasonal correlogram showing periodic stochasticity/intermittency.
the fact the series takes on nonzero and zero values throughout the entire length of the record (Figure 6).
In the same context, figure 8 shows inter-annual decadal variation in the rainfall series; long-term trend pattern is seemingly not evident. However, there is large variability among the monthly values of rainfall of different years, with the period 1995-2009 showing slight increases in the storm event during the peak seasons. On the other hand, figure 9, figure 10 shows the presence of seasonality in the moments, meaning that monthly statistics for dry season are significantly different from those of the wet season period. Unlike intermittent stream flow process, the seasonal means have higher values than the seasonal deviations throughout the year. As noted in Figure 10, the coefficient of variation varies from 0.3234 in the month of June to 3.4227 in December (i.e., period of incipient rains, moderate-peak to late rains). The variance is maximum during the period of late rains and incipient dry season; more or less the interfacing period. This indicates atmospheric instability during this watershed period; i.e., the fringes of the raining season going to full harmattan period. Similarly, as shown in Table 3, values of the skewness coefficient (g) for the periods of incipient dry season (late rains) to full dry season are generally larger than the corresponding periods for the wet season over an annual cycle. This indicates that the data in the former seasons depart more from normality than those in the later (early to full wet season period). The variability in the time series regime leads to model structural uncertainty; especially if the hydrologic evolution of the generating mechanism is not appropriately understood and captured in the model formulation.
To assess this, analysis of dependence structure in time series via spectral density is critical; figure 11 shows the dependence structure of the monthly rainfall in a frequency domain. The spectral density exhibits a discrete spectral component at the frequency of 1/12 cycle per month. This periodicity is seen in figure 11(a). Similarly, the periodogram exhibits quite a corresponding pattern in terms of the periodicity. However, as noted by Kottegoda [1] , interpretation is difficult as it provides unexpected peaks. From figure 11(b), the sample spectra from the different sections of the rainfall data may resemble each other in their overall aspects.

Figure 8. Inter-annual mean monthly rainfall variation pattern.

Figure 9. Variation in seasonal moments.
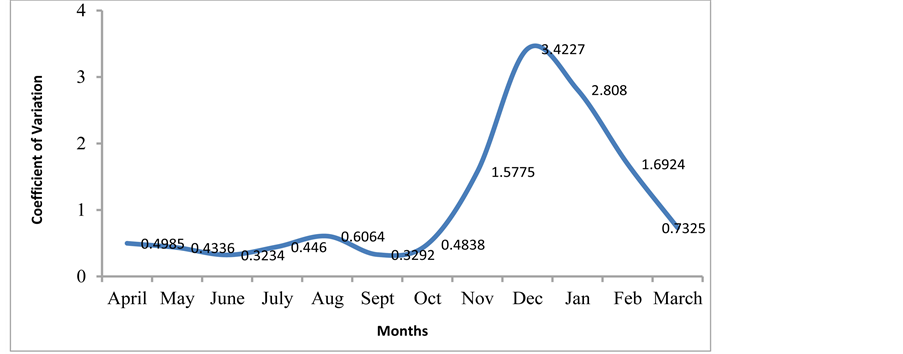
Figure 10. Seasonal pattern in coefficient of variation.
3.2. Modelling and Forecasting of the Rainfall Regime
Figure 12 shows the behaviour of the different model forecast functions; the forecasts are quite at variance with the expected. Baring data quality problems, stationarity issues, and model over fitting, forecasts in the distant future for a trend-free series should be the unconditional estimates of the means. From figure 12, it’s obvious that the performance of the different modelling schemes can be expressed in this order: T-F > Composite > Square root transformation-Deseasonalised > Decomposition. Table 4 and figure 13, respectively show the performance of the modelling scheme with respect to the ability to represent the seasonal statistics of the observed rainfall series. It is apparent from figure 13 that for the entire lag time considered, models T-F, Square root transformation-deseasonalisation and Composite were able to replicate the measured rainfall pattern, though
 (a) (b)
(a) (b)
Figure 11. Spectral density based on Tukey lag window (a) and the periodogram (b) of the raw monthly rainfall series.
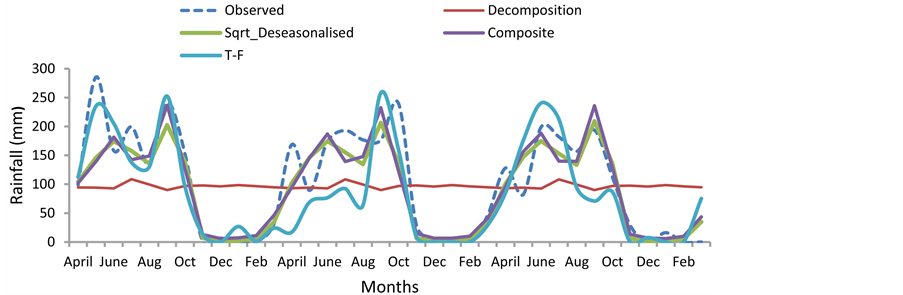
Figure 12. Summary chart of the different models’ behaviour in forecsat mode vis-à-vis the observed mean monthly series.
to varying degrees of accuracy whereas the decomposition strategy failed completely. In above, the positive attribute of the T-F model ahead of others reinforces its suitability for adoption in rainfall modelling.
Table 4. Seasonal moments for both the observed series and the models in the simulation phase.
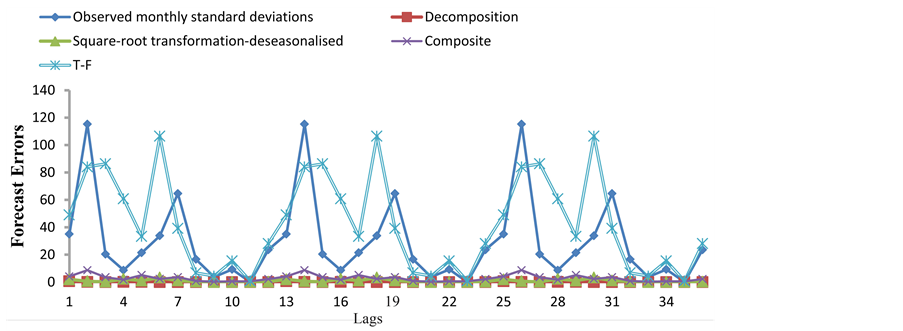
Figure 13. Monthly standard deviations of the rainfall series and forecast errors of the ARIMA models for the respective modelling schemes.
Considering the performance of the models adopted, it is imperative to look at the implications of the data pre-processing strategy. In all the models, except the Thomas-Fiering (T-F) model, ARIMA models were used to model the supposedly stationary stochastic component. To achieve stationarity, seasonal differencing (12-lag) and seasonal standardisation (deseasonalisation) were respectively applied but not without its associated problems. For instance, the deseasonalisation process is a misnomer since it implies that the deseasonalised series is free of seasonality; however, other seasonality may still be present [12] [15] . Seasonal differencing on the other hand, removes the periodic contribution but the spectral density obtained thereof has a sinusoidal shape, also the covariance of the stationary part is distorted. In the same context, the multiplicative ARIMA model assumes there is a serial correlation structure within the months of the same year but it does not preserve the monthly standard deviations just like the others as seen in figure 13. Thus within this context, the overall poor performance of all the models with the exception of T-F could be understood.
4. Conclusions
For purposes of identifying a more realistic modelling scheme for the rainfall series, assessment of the stochastic characteristics was done to be able to understand the dynamics of the monthly series. Sequel to this, four different modelling schemes: Decomposition, Square root transformation-deseasonalisation, Composite, and Periodic autoregressive modelling (T-F), were adopted. Results of basic analysis of the stochastic characteristics revealed that the monthly series does not show any discernible presence of long-term trend, though there is a seeming inter-decadal annual variation. It is evident that the series exhibits strong seasonality throughout its length, both in the moments and autocorrelation. This gives rise to significant correlation which is attributable to the serial dependence of the same month on several years; this serial dependence is same for all 12 months. The strong seasonal autocorrelation structure connotes intermittency considering the fact that the series assumes nonzero and zero values throughout its length for the period considered.
Resulting from the analysis and the modelling exercise, the Thomas-Fiering (T-F) model can be used for monthly rainfall modelling and short-term forecast. In addition, both the composite and square root transformation-deseasonalisation schemes may also be employed but not without caution. Because of the ARIMA model component of these models in the coupling, their forecast abilities were impaired considering the inadequacy of their respective forecast errors to preserve the observed standard deviations of the rainfall series. This primarily might have arisen from the second-order stationarity assumptions requirement of the autoregressive models. In the same vein, whole decomposition of any trend-free series requiring de-trending, deseasonalisation followed by moving average smoothing, and fitting of ARIMA model might be too excessive as it distorts the entire spectrum in the overall and not encouraged. The results obtained suggest that modelling of monthly rainfall series in the presence of serial correlation between months should be based on the establishment of conditional probability framework; in this case, two conditional probabilities: probability that month t has zero rainfall given that month t-1 had non-zero rainfall and probability that month t has zero rainfall, given that month t-1 had zero rainfall. On the other hand, considering the inadequacy of these modelling schemes because of the autoregressive model components, nonlinear deterministic methods such as Artificial Neural Network, Wavelet models could be viable complement to the linear stochastic framework.
References
- Kottegoda, N.T. (1980) Stochastic Water Resources Technology. Macmillan Press Ltd., London, 2-3, 21, 112-113.
- Ramana, R.V., Krishna, B. and Kumar, S.R. (2013) Monthly Rainfall Prediction Using Wavelet Neural Network Analysis. Journal of Water Resources Management, 27, 3697-3711. http://dx.doi.org/10.1007/s11269-013-0374-4
- Georgiou, E.F. and Krajewski, W. (1995) Recent Advances in Rainfall Modelling, Estimation, and Forecasting. US National Report to International Union of Geodesy and Geophysics, 1125-1137.
- Gupta, V. and Waymire, E. (1993) A Statistical Analysis of Mesoscale Rainfall as a Random Cascade. Journal of Applied Meteorology and Climatology, 32, 251-267. http://dx.doi.org/10.1175/1520-0450(1993)032<0251:ASAOMR>2.0.CO;2
- Holley, R. and Waymire, E. (1992) Multifractal Dimensions and Scaling Exponents for Strongly Bounded Random Cascades. The Annals of Applied Probability, 2, 819-845. http://dx.doi.org/10.1214/aoap/1177005577
- Pavlopoulos, H. and Kedem, B. (1992) Stochastic Modelling of Rain Rate Processes: A Diffusion Model. Communications in Statistics. Stochastic Models, 8, 397-420,
- Jimoh, O.D. and Webster, P. (1996) The Optimum Order of a Markov Chain Model for Daily Rainfall in Nigeria. Journal of Hydrology, 185, 45-69. http://dx.doi.org/10.1016/S0022-1694(96)03015-6
- Gregory, J.M., Wigley, T.M.L. and Jones, P.D. (1992) Determining and Interpreting the Order of a Two State-Markov Chain: Application to Models of Daily Precipitation. Water Resources Research, 28, 1443-1446. http://dx.doi.org/10.1029/92WR00477
- Koutsoyiannis, D. (1992) A Nonlinear Disaggregation Method with a Reduced Parameter Set for Simulation of Hydrologic Series. Water Resources Research, 28, 3175-3191. http://dx.doi.org/10.1029/92WR01299
- Lovejoy, S. and Schertzer, D. (1990) Multifractals, Universality Classes and Satellite and Radar Measurements of Clouds and Rain Fields. Journal of Geophysical Research, 95, 2021. http://dx.doi.org/10.1029/JD095iD03p02021
- Otache, M.Y., Ahaneku, I.E. and Mohammed, S.A. (2011) Parametric Linear Stochastic Modelling of Benue River flow Process. Open Journal of Marine Science, Scientific Research, 1-9.
- Delleur, J.W. and Kavvas, M.L. (1978) Stochastic Models for Monthly Rainfall Forecasting and Synthetic Generation. Journal of Applied Meteorology, 17, 1528-1536. http://dx.doi.org/10.1175/1520-0450(1978)017<1528:SMFMRF>2.0.CO;2
- Bhakar, R.S., Singh, R.V., Chhajed, N. and Bansal, A.K. (2006) Stochastic Modelling of Monthly Rainfall at Kota Region. ARP Journal of Engineering and Applied Sciences, 1.
- Chebaane, M., Salas, J.D. and Boes, D.C. (1992) Product Autoregressive Process for Modelling Intermittent Monthly Streamflows. Water Resources Research, 28.
- Otache, M.Y., Ahaneku, I.E. and Mohammed, S.A. (2011) ARMA Modelling of Benue River Flow Dynamics: Comparative Study of PAR Model. Open Journal of Modern Hydrology, Scientific Research, 1, 1-9.
Appendix
ARIMA Model Diagnostics
NOTES
![]()
*Corresponding author.


