Received 10 December 2013; revised 10 January 2014; accepted 17 January 2014

ABSTRACT

Glaciers from the West side of the Royal Andes are an important source of fresh water for some of the most important Bolivian cities like El Alto. Temperature is an important datum for hydrological modelling and for glacier melt estimation. All temperature measurement devices have some degree of uncertainty due to systematic errors; thus, any temperature measurement has some errors. It is important to estimate the influence of such errors on the results from hydrological models and the estimation of melt water. The present study estimates the melt water contribution from the glaciers Tuni and Huayna West as a source of water supply for human consumption of El Alto considering the errors from temperature measurements. The hydrologic response of the basins was simulated with a hydrologic model. The glacier melt contribution was estimated as the difference between the discharge from the current scenario (with glaciers) and the discharge from a scenario without glaciers. Several volumes of melt water were estimated considering the temperature measurement and its possible errors. The uncertainty of such melt water volume was addressed by performing a Monte Carlo analysis of the possible melt water. The melt water contribution from glacier Tuni and Huayna West during the hydrologic year 2011-2012 was between 1.37 × 10⁶ m³ and 1.72 × 10⁶ m³. Such water volume is enough to meet the yearly water demand of between 6.81% and 8.55% of El Alto.

Keywords:

Melt water; temperature; measurement errors; uncertainty; Monte Carlo; water supply

1. Introduction

Glaciers are an important source of freshwater in the mountainous river basins of the Andes. For example, in the Bolivian Altiplano important populated cities like El Alto (68.2˚W, 16.5˚S) developed above 4000 meters above sea level (m. a. s. l.) and close to glacier areas. The city of El Alto relies on water from glacierized basins. Water is so valuable that El Alto people is decided to do any sacrifice in order to defend their right to water, as already happened in previous years when El Alto defied one of the largest water multinationals in the water world [1] . Unfortunately, glacier retreat was reported all around the world [2] - [4] . Changing hydrological conditions due to glacier retreat will affect water supply, economic activities and the environmental equilibrium [5] . Thus, the long term availability of water in El Alto is sensitive to climate variability and glacier retreat. Therefore, it is important to assess the impact of climate change and glacier retreat on the hydrology and water resources of the basins that supply water for El Alto. One important step for such goal is the estimation of melt water contribution to the total discharge.

One approach for analyzing the impact of climate change and glacier retreat on the water resources of glacierized basins is the use of hydrological models and comparing the hydrological simulation of current conditions with the hydrological simulation of future conditions without glaciers [6] - [8] . One important datum for such models is temperature. Usually temperature is obtained from field measurements. Nevertheless, temperature measurements are affected by systematic errors of the equipment that should be considered [9] - [12] . Considering that Andean glaciers are particularly sensitive to temperature changes [13] , such temperature errors may be an important source of uncertainty.

In the present study, we aim to estimate the glacier melt water contribution from the Tuni and Huayna West glaciers as a source of water supply for the human consumption of El Alto during the hydrological year 2011- 2012; unlike traditional analysis that consider the measured temperature as the true value, the present study considers the systematic errors of the temperature measurements and quantifies the melt water contribution considering the whole range of possible true temperature values. The melt water contribution was estimated by simulating the hydrological response of the basins under the current condition (with glaciers) and the hydrological response of the basins under a future scenario without glaciers. The uncertainty of the possible volumes of melt water contribution due to temperature errors was addressed by performing a Monte Carlo analysis of the possible melt water volumes. Section 2 provides a short description of the study area and the meteorological equipment. Section 3 describes the methodology; the hydrological model that was used, the parameterization of temperature measurement errors and the Monte Carlo analysis. Section 4 presents the main results. Section 5 pre- sents the conclusions.

2. Study Area

The present study analyses the melt water contribution of the basins Tuni and Huayna West. The study area is located in the Bolivian Altiplano some 25 km North of El Alto. The study area is within the Capricorn tropic. The wet season is coincident with the austral summer (October to March) when the inter-tropical convergence zone (ITCZ) oscillates over the Bolivian Amazonia; on the other hand, the dry season is coincident with the austral winter (April to September), characterized by air stability and lower availability of water vapor [14] . The hydrological year is from September to October. This is a mountainous region with elevations ranging from 4500m.a.s.l. to 6000 m.a.s.l. The study area is divided into three basins: Tuni, Condoriri and Huayna West. The basins are composed by glacierized areas, bare ground areas and wetlands areas. The basins are located in the West side of the Royal Cordillera in the Bolivian Andes. The Royal Cordillera separates the cold dry Altiplano in the West from the warm wet Amazonian basin in the East. The discharge from the basins flows towards the Tuni reservoir that has a capacity of 21.55 × 10⁶ m³. The Tuni reservoir is one of the most important water supply reservoirs for the city of El Alto. Besides, the discharge from the basins is important for the ecologic equilibrium of the wetlands. The basins are being studied by the Glacier Retreat impact Assessment and National policy Development (GRANDE) project since 2011.

The present study considered the basins Huayna West and Tuni. The Condoriri basin was not considered because of the reservoir effect of the ChiarKhotalake which is part of a separate analysis. In July 2011 the GRANDE project installed meteorological stations equipped with a HOBO-U30 data logger. The stations record automatically every 10 minutes several meteorological data such as precipitation, solar radiation, wind velocity or relative humidity. Precipitation is measured with a HOBO Pendant Event data logger integrated into a tipping-bucket rain gauge (TBRG) with an upper orifice of 15.24 cm diameter, a tip resolution of 0.2 mm and a time resolution of 10 minutes; both resolutions are within the suggested ranges for this kind of RG [15] . Wind speed is measured with a HOBO wind speed smart sensor using a three cup anemometer. It measures wind speed in a range between 0.0 m s⁻¹ and 45.0 m s⁻¹. It reports the average wind speed every 10 minutes. The TBRG were installed at the same level as the anemometers. Temperature is measured using a HOBO temperature smart sensor with a measurement range between −40˚C and 75˚C and a resolution of 0.02˚C. The stations were installed in the basins Huayna West and Condoriri. Due to the closeness of the Tuni basin and the Condoriri basin, the data from the Condoriri stations was assumed as representative for the Tuni basin. Besides the meteorological stations, three weir gauging stations were installed; one in each basin. The data from the weir gauging stations and the meteorological stations was processed and expressed at hourly data. Table 1 shows the areal distribution of each basin considering the weir stations as the outlet of the respective basin. Figure 1 shows the study area.

3. Methodology

The melt water contribution was estimated by simulating the hydrological response of the basins considering two scenarios: one current scenario with glaciers (HG) and one scenario without glaciers (HNG). The present study used the hydrological model Supertank. The model was calibrated under the current condition (with glaciers) for the hydrological year 2011-2012 and considering the temperature measurements. Then, the hydrological simulation was performed assuming a scenario without glaciers. Then, the whole range of possible temperature measurements errors was estimated according to the specifications of the equipment. The uncertainty due to the possible temperature errors was addressed by performing a Monte Carlo (MC) analysis:

· The temperature measurements were corrected by sampling one random possible temperature error.

· Then, a hydrological simulation was performed considering the scenario with glaciers and the corrected temperature (HGCT).

· The melt water contribution according to that simulation was estimated as the difference between the water volume from HGCT and the water volume from HNG.

· Then, temperature measurements were corrected by sampling another random possible error.

· Then, a new hydrological simulation was performed considering such error (HGCT + 1).

· The melt water contribution according to the new simulation HGCT + 1 was then estimated.

· The last three steps were repeated until MC analysis reached convergence in the melt water mean volume and the melt water volume standard deviation.

· Then, the melt water contribution was estimated considering the 95% and 5% confidence intervals.

3.1. Hydrological model

The present study used the hydrological model Supertank which has been applied to other hydrological studies [16] [17] . This is a conceptual semi-distributed model. The basin is semi-distributed as described by [18] ; every river cell is considered as the outlet of a sub-basin composed by all the grid cells upstream of such river cell. Every sub-basin grid cell is simulated based on the tank concept [19] improved by including physical base features [20] ; every grid cell consists of three vertical tanks and the uncertainties are transferred into one calibration coefficient. Then, the discharge is routed throughout the basin to the outlet with a kinematic wave routing scheme.

The super tank model considers different hydrological response for different ground types: bare ground, impoundments and glacier [21] . In the bare ground cells the actual evapotranspiration is extracted from the top tank as a function of the potential evapotranspiration and the water available at such tank, similar to the method

proposed by [22] . The conversion relation between potential evapotranspiration (PET) and actual evapotranspiration (AET) requires a welting point threshold and a field capacity threshold. The wilting point and the field capacity threshold were expressed as a saturation percentage of the soil. The field capacity and the wilting point were assumed as 46% and 20% respectively, as they are typical values suggested for clay soils [23] . In the wetland cells the AET extracts water from the bottom tank. AET from wetland cells is equal to the PET since any water deficit is replaced by water from the saturated zone [24] . The glacier cells do not consider evaporation since sublimation influences the mass balance, but not the hydrologic response of the cell. The discharge from glacier cells is separated into a fast englacial flow from surface, delayed englacial flow and a subglacial flow [25] . Thus, the linear cascade of 3 vertical tanks is also applied, but with a correction factor accounting for different hydraulic conductivity. Figure 2 shows the linear cascade of the three vertical tanks. Due to the lack of vegetation there is no interception on the bare ground cells. It is important to note that the model assumed that land cover does not change during the simulation, i.e., the area covered by glacier remains constant. The dynamic glacier evolution process will be covered by further research. The Supertank model requires two kinds of data: meteorological data and geographical data.

3.1.1. Meteorological data

This data refers to the external meteorological conditions of the basin. It consists of time series data of precipitation, glacier melting and potential evapotranspiration. Precipitation was obtained from the tipping bucket rain gauges. The wind induced errors of the precipitation measurements were corrected according to the World Meteorological Organization [26] . However, such measurements are point ones. The spatial distribution of precipitation was obtained by considering that precipitation increases with elevation at a rate of 0.24 mm m⁻¹ [27] .

Glacier ablation was obtained considering the energy balance method [28] [29] .

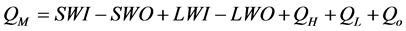(1)

where Q_M is the energy flux available for ablation (W m⁻²), SWI is the incoming short wave radiation (W m⁻²),

LWI is the incoming long wave radiation (LWR) (W m⁻²), SWO is the outgoing short wave radiation (W m⁻²), LWO is the outgoing LWR (W m⁻²), Q_H is the sensible heat flux (W m⁻²), Q_L is the latent heat flux (W m⁻²), and Q_o are other minor heat fluxes like rain (W m⁻²). Since the energy from Q_o is small compared to the other sources of energy, it was neglected. The turbulent and sensible heat fluxes were estimated according to the bulk aerodynamic approach. Sensible heat flux was calculated according to:

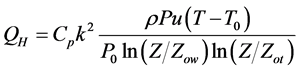(2)

where C_p is the specific heat air at constant pressure (1010 J/kg K), k is the Von Karman constant (0.41), ρ is the air density (1.29 kg/m³), P is the atmospheric pressure (Pa), u is the wind speed (m/s), P_o is the standard atmospheric pressure (101325 Pa), Z is the instrument height (m), Z_ow is the roughness for wind logarithmic profile (m), Z_ot is the roughness for temperature logarithmic profile (m), T is the local temperature (K), T₀ is the freezing temperature (273.15 K). The latent heat flux was calculated according to:

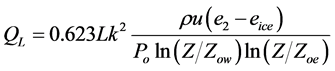(3)

where L is the latent heat flux of evaporation or sublimation (kJ/kg), e₂ is the vapour pressure at 2 m (Pa), e_ice is the vapour pressure at melting surface (Pa), Z_oe is the roughness parameter (m). The roughness coefficients were assumed as Z_oe = Z_ot = Z_ow/10; Z_ow=10 mm [30] .

The total energy available for ablation was converted into its water equivalent by considering the latent heat of fusion (334 kJ/kg) in the case of melting or the latent heat of sublimation (2838 kJ/kg) in the case of sublimation. It is important to differentiate melting from sublimation because melting glacier enters the basin as water; on the other hand, sublimation does not enter the basin and goes directly to the atmosphere. Energy is used for sublimation when latent heat flux is negative [31] . The sign of such flux is defined by the vapour pressure at 2 m and the vapour pressure at melting ice surface. Vapour pressure at 2 m was estimated by [32] :

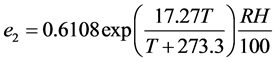(4)

The vapour pressure of melting ice was computed by [33] :

(5)

where T₀ is the freezing temperature (0˚C) in Kelvin degrees (273.15 K). Thus, the vapour pressure of melting ice is 611.15 Pa. Any meteorological conditions of temperature and relative humidity that result in a vapour pressure lower than 611.15 Pa will produce sublimation.

Potential evapotranspiration was obtained according to the Priestley-Taylor method [34] .

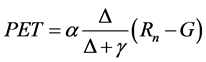(6)

where R_n is the solar radiation(W m⁻²), G is the ground flux(W m⁻²), G is the slope of saturation vapour pressure [kPa ˚C⁻¹], Δ is the psychrometric constant [kPa ˚C⁻¹], γ is the coefficient that relates the aerodynamic evaporation as a percentage of the radiative evaporation (1.74). Ground flux was assumed as percentage of the net radiation [35] . γ is given by:

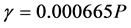(7)

where P is the atmospheric pressure (kPa). The value of Δ is given by:

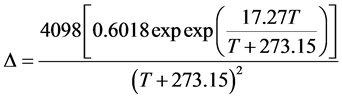(8)

where T is the air temperature (˚C).

3.1.2. Geographical data

It consists on the data representing the landforms and physical characteristics of each basin. This data is used for the semi distribution of the model. It consists of different raster files. The respective raster files were obtained using a digital elevation model (DEM) from the ASTER mission. The DEM was processed with the TauDEM algorithm implemented in the GIS software MAPWINDOWS [36] .

Other important raster file is the one defining the land cover of the grid cells. This file was obtained by processing remote sensing data from the Advanced Visible and Near Infrared Radiometer type 2 sensor (AVNIR-2) of the Advanced Land Observation Satellite (ALOS). The ALOS AVNIR-2 images were processed using the multispectral image data analysis system software [37] . Figure 3 shows the raster maps used in the present study.

The only geographical data that was not obtained from the rasters is the hydraulic conductivity. Hydraulic conductivity was obtained from field measurements using the minidisk infiltrometer [38] . The assumed hydraulic conductivity was 0.04 cm h⁻¹.

3.2. Modelling

The model was calibrated at the Tuni basin considering the hydrological year 2011-2012. Then, the model was validated at the Tuni basin for the hydrologic year 2012-2013 and at the Huayna West basin for the hydrologic

year 2011-2012 (Table 2). The performance of the model was evaluated according to the Nash Sutcliffe Efficiency (NSE), root mean square error ratio (RSR), percentage bias (BIAS) and correlation coefficient(CC) [39] - [41] . NSE is calculated by:

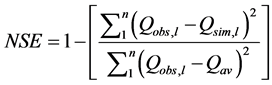(9)

where Q_obs,l is the observed discharge [m³ s⁻¹] at time step l, Q_sim,l is the simulated discharge at time step l and Q_av is the average discharge [m³ s⁻¹].

RSR is calculated by:

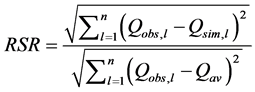(10)

The BIAS is calculated by:

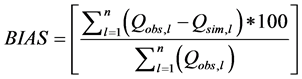(11)

The CC is calculated by:

(12)

where Q_sav is the average simulated discharge (m³ s⁻¹).

In order to have an evaluation of the glacier melt water, two scenarios were modelled and compared: one current scenario including glaciers and one hypothetical scenario without glaciers. For the scenario without glaciers, all the glacier cells were assumed as bare ground cells. The meteorological conditions of both scenarios were the same. The total volume of water discharge from the simulation without glacier (VNG) was estimated:

(13)

The melt water contribution of both basins during the hydrological year 2011-2012was estimated.

3.3. Temperature uncertainty

The present study considered temperature measurements from a HOBO temperature smart sensor. This sensor has a measurement range between −40˚C and 75˚C with a resolution of 0.02˚C. The accuracy of the sensor varies with temperature [11] and the possible temperature measurement errors are estimated by:

(14)

where t_m is the measured temperature (˚C) and t_e is the error of the measured temperature (˚C). Then, the real but unknown temperature can be expressed by the corrected temperature t_c (˚C):

(15)

The uncertainty induced by temperature was addressed by performing a Monte Carlo (MC) analysis. The MC analysis was performed by running the hydrological model s multiple times considering different values of temperature. Then, the total cumulated discharge of each simulation was calculated:

(16)

where V^s is the total water volume from the simulation s, Q_i,^s is the hourly discharge at time step i of the simulation s and n is the total number of time steps. The melt water contribution from simulation s (MV^s) was estimated as the difference between the cumulated discharge with glaciers (V^s) and the cumulated discharge without glaciers (VNG).

(17)

The MC analysis included a convergence analysis considering the variation of the mean and standard deviation as the number of iterations increases [42] [43] .

(18)

(19)

where MMV_k and MSD_k are the mean and standard deviation of the melt water up to the k^th run. Then, the hydrological simulations from the confidence levels of 95% and 5% were selected as the upper and lower confidence estimations respectively. The melt water was then estimated as the difference between the volume from the simulation with glaciers and the volume from the simulation without glaciers.

4. Results

4.1. Hydrological model calibration

The hydrological model Supertank was initially applied to the Tuni basin for the hydrological year 2011-2012. Once it was satisfactorily calibrated it was validated at the Tuni basin for the hydrological year 2012-2013 and at the Huayna West basin for the hydrological year 2011-2012. The Supertank model was calibrated considering the measured temperature. Table 3 shows the parameters of the calibrated model. Table 4 shows the performance of the model. Figure 4 shows the observed and simulated hydrographs for the calibration period. Figure 5 and Figure 6 show the observed and simulated hydrographs at the Tuni basin and the Huayna West basin for the verification periods.

4.2. Temperature errors

Figure 7 shows the maximum possible temperature measurement errors for both basins. In both stations the errors during winter are higher than the errors during summer. Between November and March, the errors at the Condoriri station are almost constant of ±0.21˚C. On the other hand, the errors for those same months at the Huayna West station are quite higher, with more errors higher than ±0.21˚C.

The hydrological model was applied to the basins Tuni and Huayna West considering the possible errors due to temperature measurements. The uncertainties of the temperature errors were addressed by applying a MC analysis. The melt water contribution was estimated considering the temperature measurements and the possible errors. The temperature measurement errors were sampled according to a uniform distribution considering the whole range of possible errors. The average cumulated discharge and standard deviation of the cumulated discharge are stable after 1500 iterations in the case of Tuni (Figure 8) and after 1000 iterations in the case of Huayna West (Figure 9). Thus, 1500 iterations is a reasonable number of simulations that provides reliable results.

4.3. Glacier melt water

Figure 10 shows the monthly melt water contribution for the hydrological year 2011-2012 considering the 5% and 95% confidence intervals for the basins Tuni and Huayna West. Although the winter months have the highest errors, the highest uncertainty in melt water contribution occurs during the summer months (wet season). The yearly melt water contribution from the Tuni and Huayna West basins during the hydrological year 2011-2012 was between 1.37 × 10⁶ m³ and 1.72 × 10⁶ m³ (Table 5). Comparing with the total observed discharge, the total melt water contribution accounts for about 13.45% of the total discharge (5% confidence) and 17.01% of the total discharge (95% confidence).

4.4. General Discussion

According to the parameterization of the systematic errors, temperatures lower than 0˚C have higher errors than temperatures above 0˚C. For this reason, in both basins the highest temperature errors occur during the dry season months (between April and September) which is coincident with the winter. During the winter months the freezing temperatures below zero occur more often. Figure 11 shows that during winter 40% of the temperature measurements from the Huayna West station are below 0˚C and 30% of the temperature measurements from the Condoriri station are below 0˚C. On the other hand during summer months the occurrence of freezing temperatures is lower than 5%. The measurement errors at the Huayna West station are higher than the errors at the Condoriri station. This is because the Huayna West station is located at higher elevation and has lower temperatures than the Condoriri station. Thus, temperature measurement devices installed at higher elevations are prone to higher errors.

Although temperature errors are higher during winter, uncertainties related to melt water contribution are higher during summer. This is because during winter most of the ablation is due to sublimation [44] which goes to the atmosphere. Thus, the total amount of melt water during winter is minimum.

The melt water contributed from glaciers is higher during the wet season, which is coincident with the austral summer. 87% of Tuni melt water contribution occurs during the wet season (October to March) and 81% of the Huayna West melt water contribution occurs during the wet season. It is important to remember that the seaso-

nality of the area is defined not by temperature cycles, but by hygric conditions [45] defined by the seasonal oscillation of the inter-tropical convergence zone (ITCZ). During the austral winter the ITCZ is north and the study area has a clod dry season; but during the austral summer the ITCZ is south. During the summer months the ITCZ oscillates over the Bolivian Amazonia coincident with the eastern inter-tropical flux that brings water vapor from the so called Amazon Ocean [14] . Thus, the wet season coincides with the eastern inter-tropical flux that brings water vapor from the Atlantic [46] . For this reason the relative humidity during summer is much higher than the relative humidity during winter. This higher relative humidity influences the amount of energy used for melting. Melting occurs when the vapor pressure is higher that the vapor pressure at melting surface [31] . Water pressure in turn depends on temperature and relative humidity. The small temperature variation of tropical latitudes leads to small increments of water pressure; thus, temperature increase does not increase the energy used for melting. On the other hand, the higher relative humidity of the wet season will lead to higher increments in the vapor pressure; thus, there is more energy used for melting.

The total melt water contribution for the hydrological year 2011-2012 was between 13.45% and 17.01% of the total discharge. The comparison of such contribution with contributions from other tropical glaciers is quite difficult, because there are few studies to compare and the high variability of melt water contribution. One tropical glacierized basin with a similar degree of glaciation is the Rio Santa in the Cordillera Blanca (Peru) which is about 10% glacierized (in the present study the glacier area is about 10.1% of the total area). Studies from the Rio Santa showed a high variability of the melt water contribution. The melt water contribution from Rio Santa during the hydrological period 1998-1999 was between 12% and 20% [47] ; but the melt water contribution for the hydrological period 2001-2004 was between 30% and 40% [48] . For the same periods and the same river (Rio Santa), other studies [49] estimated the melt water to be between 16.5% and 20.1%. The melt water contribution from the present study is similar to the mentioned ranges (Table 6). Nevertheless, the present estimation seems a low one compared with estimation of the Rio Santa for the period 2001-2004. Such difference may be due to the fact that Rio Santa is located in the inner tropics where the melting is constant throughout the year, while the present study is located in the outer tropics where melting occurs mainly during the wet season [13] .

Unlike other tropical glacier studies that estimated melt water contribution, the melt water contribution from the present study is directly related to the human consumption of a big city (El Alto). Thus, it is also important to express the melt water contribution related to human consumption (Table 7). Considering the population of El Alto (1182319 habitants) and that the estimated water demand of El Alto is about 46.7 l habitant⁻¹ day⁻¹ [50] , the melt water contributed by the Tuni-Huayna West glaciers is equivalent to the yearly demand of 6.81% to 8.55% of the city of El Alto (between 80497 habitants and 101148 habitants respectively).

5. Conclusions

The present study analyzed the melt water contribution from the Glaciers Tuni and Huayna West to their respective basins considering the systematic errors of the temperature measurements. Melt water contribution from the Tuni and Huayna West glaciers was estimated for the hydrologic year 2011-2012.

The hydrological model Supertank was satisfactorily applied to the basins Tuni and Huayna West. Then, the hydrological model was applied considering a scenario without glaciers. The melt water contribution was estimated as the difference between those scenarios.

The temperature measurement errors are higher during freezing temperatures. Thus, the temperature measurements from winter months have higher errors. Temperature measurements from higher elevations (lower temperatures) are expected to have higher errors.

Most of the melt water contribution occurs during the wet season months (October to March). 87% of melt water from Tuni glacier occurs during the wet season and 81% of the melt water contribution from the Huayna West glacier occurs during the wet season.

Although temperature measurement errors are higher during the dry season, the melt water contribution un-

certainties due to temperature measurement errors are higher during the wet season. This is because during the dry season the total melting is reduced to its minimum.

The melt water contribution from the Tuni and Huayna West glaciers during the hydrological year 2011-2012 was between 1.37 × 10⁶ m³ (for a 95% confidence) and 1.72 × 10⁶ m³ (for a 5% confidence). Such volumes are equivalent to 13.45% and 17.01% of the total discharge.

The melt water contribution from the Tuni and Huayna West glaciers during the hydrologic year 2011-2012 was equivalent to the yearly water demand of 6.81% to 8.55% of El Alto (Bolivia). Those percentages are equivalent to 80497 habitants and 101148 habitants respectively.

Acknowledgements

This research is developed within the framework of the GRANDE project, financed by SATREPS from JST- JICA. We thank PRAA project for the ALOS data.

References

NOTES

^*Corresponding author.