Open Journal of Forestry
Vol.06 No.01(2016), Article ID:61791,13 pages
10.4236/ojf.2016.61001
Tanoak (Notholithocarpus densiflorus) Coarse Root Morphology: Prediction Models for Volume and Biomass of Individual Roots
Brandon H. Namm*, John-Pascal Berrill
Department of Forestry and Wildland Resources, Humboldt State University, Arcata, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 October 2015; accepted 6 December 2015; published 9 December 2015
ABSTRACT
Descriptions of tree root morphology inform design of belowground biomass and carbon inventories and sampling for research. We studied root morphology of tanoak (Notholithocarpus densiflorus), an important component in mixed evergreen forests of California and Oregon, USA. Tanoak re-sprouts from belowground lignotubers after disturbances, and stores an unknown amount of carbon in coarse roots underground. We sought to ascribe explanatory nomenclature to roots’ morphological features and to identify models describing tanoak root morphology. Twelve tanoak root systems were excavated, dissected, and measured. Roots tapered according to their circumference and location. Larger roots closer to the lignotuber (located at the base of the tree stem) tapered more rapidly per unit of length. Tanoak roots forked frequently. Root cross-sectional area was preserved after forking events (i.e., the sum of cross-sectional areas for smaller roots on one side of the fork correlated with the adjoining large root). Occurrence and quantity of root bran- ches (small roots branching laterally from larger roots) was dependent upon length of the source root segment. Our models of tanoak root morphology are designed to be organized together to estimate biomass of any segment or collection of lateral roots (e.g., roots lost/missed during excavation, or in lieu of destructive sampling), given root diameter at a known distance from the lignotuber. The taper model gives distal- and proximal-end diameters for calculation of volume for segments of root tapering between forks. Frequency of forking and branching can also be predicted. Summing the predicted mass of each lateral root segment, branch, and forked segment would produce an estimate of mass for a contiguous network of lateral roots.
Keywords:
Belowground, Biomass, Carbon, Root Taper, Tree Root Architecture

1. Introduction
Tree roots are difficult to access and study, yet their important contribution to terrestrial carbon pools should be quantified. Estimates of tree root biomass and carbon content allow us to quantify impacts of land-use change and disturbances on belowground carbon pools. Tree root biomass sampling is challenging due to roots’ variable spatial distribution (Danjon & Reubens, 2008) . Descriptions of tree root morphology support the design of appropriate sampling methods for research into root structure and function.
Measuring the biomass of an entire root system requires complete excavation of the roots or removal of all soil surrounding them. An excavator can be used to remove the root-soil plate (a mass of woody tissue connecting the stem to the lateral roots), but hand tools or an air spade are required to excavate smaller more fragile roots (Bingham et al., 2001; Lavigne & Krasowski, 2007) . Excavating large root systems is particularly laborious and loss of some root biomass is likely (Böhm, 1979; Danjon et al., 2013) . Deriving total belowground biomass estimates from the excavated portions of a root system requires development of predictive models to account for the roots lost during the excavation process (Richardson & Dohna, 2003; Danjon et al., 2013) .
One approach to estimate the root biomass lost during excavation is to collect a subsample of roots and regress individual roots’ biomass against their cross-sectional area (e.g., Santantonio et al., 1977; Coutts, 1983 ). This method can be effective when a fixed area surrounding the sample tree is completely excavated and the total root mass within the excavation is measured. Roots outside the excavated area are then sub-sampled to develop a regression between the roots’ severed cross-sectional area and their biomass. Biomass for the severed roots can therefore be determined by applying the regression to the cross-sectional area at the end of all the roots severed during excavation. However, factors such as slope, soil, wind, climate and inter-specific competition from adjacent trees may affect the relationship between root cross-sectional area and mass (Nielsen & Hanson, 2006; Zanetti et al., 2015) .
Another approach to estimate biomass lost during excavation is to model root morphology. This approach allows for more accurate estimation of unexcavated root volume or mass and can form the basis of research into factors affecting biomass allocation within root systems (Nielsen & Hanson, 2006) . Previous studies have included measurements of individual root segments between forks and descriptions of the root branching patterns (Fitter et al., 1991; Noordwijk et al., 1994; Oppelt et al., 2001; Vercambre et al., 2003; Kalliokoski et al., 2010) . By describing morphology of individual root segments, root morphology for an entire belowground system can be more accurately modeled, and allometric models of belowground biomass derived (Nielsen & Hanson, 2006) .
To date, the morphology of tanoak (Notholithocarpus densiflorus) roots has not been described. Tanoak is an evergreen hardwood species that grows throughout California and southern Oregon, USA. The species is threatened by an exotic disease called sudden oak death. Tanoaknuts provide an important food source for mammals, birds and insects (Tappeiner et al., 1990) . In northwest California, tanoak is a component of stands dominated by Douglas-fir (Pseudotsuga menziesii) or coastal redwood (Sequoia sempervirens) that are favored habitat for the endangered northern spotted owl (Strix occidentalis) and their prey, the dusky-footed woodrat (Neotoma fuscipes) (Thome et al., 1999) . Tanoaks provide soil stability and prevent mass wasting of soil by re-sprouting and maintaining a live root system after harvest or wildfire. New tanoak stems can sprout from previously established lignotubers comprising a mass of buds and starch reservesat the base of the tree stem (Tappeiner et al., 1990) .
Our goal was to provide a detailed description of tanoak root morphology. We hypothesized that root taper and forking patterns were predictable, and related to root size and location within the root system. Destructive sampling gave root size data for analysis and modeling of root morphology. We present a series of models describing components of tanoak root systems. These models are designed to be applied in combination to generate predictions of lateral root volume for entire root systems or parts thereof, and subsequent conversion of volume to biomass or carbon estimates.
2. Methods
2.1. Site Description
Root systems were excavated at the L.W. Schatz Demonstration Tree Farm, near Maple Creek in Humboldt County, California (40˚46'49"N, 123˚52'21"W). The 148 ha property is located within the Klamath Mountains Geomorphic Province. Soils consist mainly of Ultisols which are strongly leached, acid forest soils with relatively low native fertility. However, due to the favorable climate regimes in which they are typically found, Ultisols often support productive forests. Ultisols have a subsurface horizon in which clays have accumulated, often with strong yellowish or reddish colors resulting from the presence of iron oxides. The Mediterranean climate is characterized by hot, dry summers with daytime high temperatures averaging 29˚C and cool, wet winters averaging 8˚C. Average annual precipitation is approximately 1200 mm, with the majority falling as rain between the months of November and March. Before harvesting in the 1950s, the site was occupied predominantly by an old-growth Douglas-fir forest with tanoak and California bay (Umbellularia californica) associates. Species composition now consists primarily of young planted and naturally regenerated Douglas-fir and naturally regenerated grand fir (Abies grandis) mixed with tanoak, and pure stands of red alder (Alnus rubra).
2.2. Excavation Methods
Twelve tanoak trees were sampled on slopes of 0% - 55% across a range of aspects. The trees were excavated using a Komatsu mini excavator with a 0.3 m bucket (Figure 1(A)). Surrounding each tree we dug a narrow trench in the shape of a 2 × 2 m square. Trench depth was approximately 1 m after digging down until tanoak roots were no longer visible. We named the 4 m2 area inside the square “the excavation area” which encompassed the tree and its root-soil plate with lateral roots severed at the trench by the excavator bucket. The root-soil plate of each tree was exposed by pulling the stem over with a truck, and cleaned using hand tools, e.g., shovel, trowel, etc. (Figure 1(B)). The aboveground stem (s) were cut off each root-soil plate, and a backhoe was used as a crane to carry the root-soil plate to the washing area (Figure 1(C)). A fire hose (with a pump rate of 75 - 340 liters minute−1) (Figure 1(D)) and hand tools were used to remove any remaining soil. Beginning on the outer wall of the trench, lateral roots heading outside the excavated area were sub-sampled based on proximity to eight cardinal directions around large trees and four cardinal directions around small trees. These roots were excavated with hand tools and washed in preparation for measurement.
2.3. Root Measurements
Roots were categorized into three groups (Figure 2). First, a main root was defined as a root segment with two
Figure 1. Excavating root systems for belowground biomass estimates. (A): Use of excavator to dig trench around tree and sever lateral roots so tree and root-soil plate could be pulled onto its side. (B): Cleaning of roots using hand tools. (C): Using tractor as a crane to move root systems from excavation site to a washing station. (D): Continued cleaning of the roots using fire hose with rate of 75 - 340 liters minute−1.
Figure 2. Nomenclature (main root, fork, root branch) used to describe morphological features of tanoak roots. In this example, the “prox-end” and “distal-end” of each root segment are at left and right ends of segment, respectively.
measurable ends growing from the root-soil plate, the excavated area, or a fork. A fork was therefore defined as a node between adjacent segments of a main root where the narrow end of a larger main root was divided into two, three, four, or five smaller main root segments. We measured the diameter of the single larger proximal root joining the fork (termed “prox-end” diameter; in closer proximity to the root-soil plate), and all the “distal-end” diameters of the main root segments connected to the opposite side of the fork (further from root-soil plate), as well as the forked segment’s length and mass. The average diameter was recorded when cross-sections were elliptical. Proximal- and distal-end fork diameters were measured at the point nearest to the fork before the root cross-section became deformed or swollen adjacent to the point of forking. Fork length was defined as the average distance between points of diameter measurement for the fork’s prox-end and each smaller distal-end. Lastly, a root branch was defined as a root segment that originated from a main root but-unlike a fork-did not alter the diameter of the main root segment. Three measurements were collected from each root segment: prox- end diameter, distal-end/s diameter, and length of the root segment.
Tapering of main root segments was quantified using a random subsample of roots within the excavated area and all the roots sampled outside the excavated area. Because fine roots were expected to contribute little to overall root biomass (e.g., 0.05% to 0.08% for roots <2 mm in diameter; Le Goff & Ottorini, 2001 ), we did not collect or measure roots <1 mm in diameter. Tanoak lignotubers were used as the starting point for root segment location measurements. The path length of each main root segment and total exterior path length from the lignotuber were measured using a cloth tape. Root branch and main root segment diameters were measured at their origin and terminus (i.e., where the root segment either forked or tapered to one mm in diameter), and the path length was measured between these diameters. Path lengths were also measured between specific diameters set at increments of 0.5 cm when the root was less than two cm in diameter and at increments of one cm for roots greater than two cm diameter. For example, path length was measured along each root between diameters of 0.5, 1, 1.5, 2, 3, 4 cm, etc. A hierarchical numbering scheme was ascribed to all associated main root segments, forks, and root branches originating from one main root leaving the lignotuber or excavated trench.
2.4. Morphology Models
Generalized linear mixed models of root morphology were constructed to account for nesting of roots within different trees. Models were fitted to root morphology data for individual tanoak trees using PROC GLIMMIX in SAS Statistical Software (SAS Institute, 2004; Littell et al., 2006) . Figures were produced using R Software (R Foundation for Statistical Computing, 2003) . Data were transformed to reduce skewness. Candidate variables tested for inclusion in the eight models of root morphology are listed in Table 1.
Table 1. Predictive variables tested in models of tanoak root morphology.
Various taper models were tested with taper rate expressed as the decrease in root diameter, cross-sectional area, or circumference cm−1 of length, expressed as a percent. A linear mixed model of taper was used to test whether taper rate differed depending on the root’s root elongation direction around the tree. To obtain an appropriate model of main root length between forks where data were extremely skewed (many short main root segments and few long), the cumulative frequency of observed length measurements (i.e., the sum of all the frequencies up to and including that value) was calculated and tested as a response variable (Kalliokoski et al., 2010) . Root size, total path length from the lignotuber (LFL, measured in cm), and cumulative frequency were tested as predictors of main root length in non-linear models fitted using PROC NLIN in SAS.
The combined cross-sectional area of all distal-ends of each fork was modeled using the prox-end cross-sec- tional area of the fork as a predictor. A fork mass model was developed to allow for future predictions of belowground biomass. The volume of main root segments and root branches can easily be estimated as a conic frustum and converted to mass for each main root segment. Forks, alternatively, could not be easily represented as a geometric shape, making their mass-estimated via volume and specific gravity-difficult to obtain. Instead, the predictive ability of variables fork length, the prox-end cross-sectional area of the fork, and the number of main roots resulting from the fork were tested to develop an empirical model of fork mass after weighing individual forked sections (oven-dried at 65˚C).
We used logistic regression (SAS PROC LOGIT) to test whether the probability of a main root producing a root branch was predictable and related to various root segment size parameters (e.g., main root length), resulting in a binary response (root branch or no root branch). The number of root branches on each main root segment was regressed against length of the main root segment by specifying a Poisson distribution to define the dependent variable in the mixed linear model. Root branch prox-end diameter was modeled as a proportion of the main root’s prox-end diameter and various main root size parameters were tested to predict root branch size (Table 1).
3. Results
Excavated tanoak represented a broad range of tree sizes. Sample trees were either single-stemmed or multi-stemmed, of dominant or suppressed crown class (Table 2). The excavated tanoak root systems had a three- dimensional form described as a “heart” system, where horizontal and vertical roots develop from the base of the tree (Stokes & Mattheck, 1996) . However, the tanoak lateral roots extended from the lignotuber, rather than directly from the base of the stem.
3.1. Main Root Segment Models
We measured the length and end diameters of 2151 main root segments to calculate root taper. Taper rate varied from 0.01% to 13.1% of the roots cross-sectional area cm−1 of length. The diameter of the largest root was 23.2 cm (circumference = 72.9 cm). This root was adjacent to the lignotuber (LFL = 0 cm) and tapered at a rate of
Table 2. Aboveground variables measured on single- and multi-stemmed tanoak excavated at the L. W. Schatz Demonstration Tree Farm in Humboldt County, California.
*Double-stemmed tanoak with separate stems at dbh but sharing a single stem at ground level.
13.1%. Using cross-sectional area as a predictor of root taper resulted in non-uniform distribution of residuals. Using circumference to predict root taper resulted in more uniformly distributed residuals. The main root’s prox-end circumference (MPC) and LFL were both highly significant predictors of root taper (p < 0.001, Table 3). The root taper model predicts rate of tapering in a root’s cross-sectional area (cm2) per cm of root length:
 (1)
(1)
The model indicated that root taper rate increased with root size and decreased with greater LFL. The cross- sectional area of a large root therefore tapered at a faster rate compared to a root with a small cross-sectional area. Larger roots located nearer to the lignotuber had a higher taper rate (Figure 3). Variation among trees accounted for only 3% of the total variation around the linear mixed-effects model of root taper, indicating that taper did not greatly differ among the sampled trees. Roots oriented northeast of the excavated trees had the highest taper rate (p = 0.051), while root elongation direction did not affect taper in the other directions.
The length of main root segments between forks ranged from zero (i.e., one fork growing immediately after another fork) to 250 cm. A non-linear model of main root length as a function of the cumulative frequency of root length data (CF) and the LFL best described main root length. The model indicated that main root length between forks increased non-linearly with greater LFL and cumulative frequency (Table 3; Figure 4), such that:
 (2)
(2)
where parameters β0 and β1 defined the rate of increase in the curve and β2 controlled the shape of the curve (i.e.,
Table 3. Main root models in tanoak-coefficients and fit statistics for fixed and random effects in a generalized linear mixed model of tanoak root taper rate as a function of the main root segment’s proximal-end circumference (lnMPC) and the path length from the lignotuber (lnLFL), and for non-linear model of tanoak root length between forks as a function of path length from the lignotuber and cumulative frequency of root lengths (CF; range: 0 - 1).
Figure 3. Relationship between taper rate, as the percent decrease in main root cross-sectional area cm−1 of length, and main root diameter in tanoak. Different lines represent varying path lengths from the lignotuber (LFL) (Equation (1)).
concave up). Including cumulative frequency as a predictor of main root length produced a modeled distribution that reflected the frequency distribution observed in the data. For a given cumulative frequency, the maximum possible predicted length of a main root segment increased with greater LFL. A main root 500 cm from the lignotuber, for example, had a maximum predicted length of 204.8 cm before forking while the maximum predicted length of a main root adjacent to the lignotuber was only 138.2 cm.
3.2. Forking Models
Among all forks measured in this study (n = 593), 87% were bifurcations resulting in two main roots, 11% were trifurcations, and 2% of the forks resulted in either four or five main roots. The prox-end cross-sectional area of a root fork (ProxCSA) was positively correlated with the sum of all “distal-end” cross-sectional areas of roots at the opposite side of each fork, such that a fork’s total distal-end cross-sectional area (DA) was:
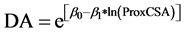 (3)
(3)
The linear regression slope coefficient (β1) was 1.08 (Table 4), indicating that total root cross-sectional area was conserved when passing through forks (Figure 5).
Fork length increased with the fork’s prox-end cross-sectional area (Table 4), such that:
 (4)
(4)
However, substantial variation among trees was present, with 36% of variation around the linear mixed-ef- fects model of fork length due to differences among trees. Fork mass increased with greater prox-end cross-sec- tional area and path length of the forked root segment (ForkLength) (Table 4, Figure 6):
Figure 4. Relationship between length of main root segments and cumulative frequency (i.e., the sum of the frequencies at or below a given length) in tanoak roots with varying path lengths from the lignotuber (LFL) (Equation (2)).
Figure 5. Combined cross-sectional area of forks’ distal- ends regressed against the proximal-end cross-sectional area in tanoak root forks (n = 593, Equation (3)). Axes presented on ln scale.
Figure 6. Combined cross-sectional area of forks’ distal-ends regressed against the proximal-end cross-sectional area in tanoak root forks (n = 593, Equation (5)). Axes presented on ln scale.
Table 4. Root fork models in tanoak―coefficients and fit statistics for fixed and random effects in generalized linear mixed models of combined distal-end cross-sectional areas (lnDA) of the fork as a function of the proximal-end cross-sectional area (lnProxCSA), tanoak fork length (FL0.5) as a function of lnProxCSA, and fork mass (lnFM) as a function of fork length (lnForkLength) and lnProxCSA.
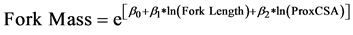 (5)
(5)
The longest fork measured was 20 cm long with a proximal cross-sectional area of 16.4 cm2 and mass of 202.3 g while the fork with the greatest mass weighed 624 g and had a prox-end cross-sectional area of 29.5 cm2.
3.3. Root Branching Models
Longer main root segments had a higher probability of producing a root branch. To produce a binary response of branching (i.e., root branch or no root branch), we used the logistic model:

where the probability of branching was the probability the main root segment would produce at least one root branch, and Main Length was the path length of the main root segment (Table 5). Comparing the logistic model to the observed data resulted in 423 correct classifications out of 589 observations (71%) compared to 328 expected correct classifications by chance (55%). Although the logistic model provided better estimates of root branching than random classification, 71% correct classifications indicated that data were highly variable. The probability of a main root segment appending at least one root branch reached 50% when the main root length was 63.8 cm. After determining whether an individual main root segment appended a root branch, we determined the number of root branches produced by the main root segment:

The number of root branches present on each sample root segment was highly variable. For example, our data included a main root 39 cm long that appended seven root branches while a main root 212 cm long appended only one root branch. Despite this variability, the number of root branches originating from an individual main root segment significantly increased with the length of that main root (Table 5). A root branch’s prox-end diameter, as a proportion of the parent main root segment’s prox-end diameter, was negatively correlated with prox-end diameter of the main root segment (i.e., a smaller main root produced a larger root branch relative to its prox-end diameter, Table 5). The model for the root branch’s prox-end diameter as a proportion of the parent
Table 5. Root branching models in tanoak-coefficients and fit statistics for fixed and random effects in generalized linear mixed models of number of root branches (lnNB) as a function of length of the parent main root segment (lnMainLength), and the proportional proximal-end root branch diameter (prox-end root branch diameter/main root’s proximal-end diameter, lnBD) as a function of the main root segment’s prox-end diameter (lnMainDiam).
main root segment’s prox-end diameter (MainDiam) was:

A root branch originating from a main root 0.5 cm in diameter, for example, was modeled as 37% of the main root’s prox-end diameter, resulting in a root branch 0.18 cm in diameter. Conversely, a main root five cm in diameter produced a root branch that was 14% of the main root’s prox-end diameter, or 0.74 cm.
4. Discussion
Root taper is an important facet of root morphology. When combining morphological models to obtain predictions of root volume, the rate at which one root segment tapers dictates input parameters of subsequent morphological models (Nygren et al., 2009; Soethe et al., 2007) . To improve descriptions of root morphology, root taper models could account for influential local environmental factors. Prevailing winds may affect root taper. The mechanical stress created by wind can directly act on woody root growth with different effects on root size, shape, and stiffness. Roots closer to the stem and root-soil plate of a shallow rooted tree species, such as tanoak, have been shown to develop irregular, rather than oval, shaped cross-sections in response to wind (Coutts et al., 1999) . Roots growing from the base of Picea sitchensis on the tree’s leeward side had less symmetrical cross- sections than the roots growing on the windward side (Nicoll & Ray, 1996) . To obtain effective support against wind, trees may also develop several large horizontal leeward roots which taper very gradually (Danjon et al., 2005) . We accounted for this source of variation in root morphology by systematically sampling roots oriented in different directions, and found that orientation had an apparent-but not statistically significant-effect on root taper. We speculated that exposure to the predominantly westerly winds was encouraging root elongation (reduced taper) in the westerly direction. However, a confounding factor likely to have affected root taper was a slope effect where sample trees had roots oriented downhill that were longer (reduced taper) than roots growing in the uphill direction; possibly investing in additional root growth downhill where water may be more abundant (Zanetti et al., 2015) .
The length of main root segments may be influenced by the availability of belowground resources and the tree’s ability to access them. Acquisition of soil-derived resources affects growth of above- and belowground components (Fitter et al., 1991) . In dry nutrient-poor conditions, individual root segments are longer, illustrating the importance of root exploration (Kalliokoski et al., 2008) . This adaptation allows root systems to become more herringbone-like (with long root segments and small exterior root branches) in low-nutrient conditions (Oppelt et al., 2001) . Root axis forking and root branch production is beneficial only if the production of additional root segments results in more efficient exploitation of soil resources (Fitter et al., 1991) . A tree growing in dry soil with variably distributed belowground resources, therefore, requires a root system with longer main root segments and fewer forks compared to a tree exploiting adequate water and nutrients from a smaller volume of soil. Our observation of many short roots between numerous forks may suggest less moisture stress experienced by the study trees relative to tanoak growing on drier sites. However, our site is relatively hot and experiences prolonged summer drought, so other factors such as shade and niche partitioning in these mixed stands may be reducing moisture stress. Intense neighbor competition may also have restricted lateral expansion of tanoak roots, forcing frequent forking to better exploit soil adjacent to the tree (Mao et al., 2015) .
During our study of tanoak root morphology we overcame operational challenges, collected novel root measurements, and modeled several morphological characteristics. Few studies have measured taper of individual root segments and quantified the size and number of root segments resulting from root forks. Although other studies of root morphology have not discriminated between root branches and forks, we found that these characteristics should be modeled separately in tanoak. Because our objective was to describe tanoak root morphology primarily for prediction of root volume and biomass, we did not attempt to describe aspects of the spatial distribution of roots, such as the angle separating the small fork ends (Kalliokoski et al., 2010) or the horizontal or vertical positioning of roots in the soil (Drexhage et al., 1999) . Nielsen& Hanson (2006) found that rooting depth helped explain variations in root taper of six tree species. We did not record depth of each tanoak root segment, but our finding that taper was affected by root orientation and size could be exploited to design a sampling protocol to collect different-sized roots at different depths and examine the relationship between root depth and taper (Danjon et al., 2013) .
Our analysis of tanoak root morphology revealed patterns that will inform future studies, and can be exploited to generate accurate predictions of volume for individual roots. The models can be applied in combination to predict biomass and carbon of individual roots lost during excavation or otherwise excluded during subsampling, or exposed in non-destructive trenches. These estimates in turn support complete summation of belowground biomass in sample trees. Accurate estimates of biomass for entire root systems are needed when studying factors affecting belowground biomass allocation. Ultimately the incorporation of influential variables into allometric models will allow for accurate prediction of total belowground biomass over a range of environmental conditions, disturbances, and forest management interventions.
Acknowledgements
We are grateful for advice provided by Chris Edgar, George Pease, Gordon Schatz, Steve Sillett, and Morgan Varner. Technical assistance was provided by Chris Beal, Matthew Cocking, Ethan Coonan, Jeromy Couch, Janina Dierks, Chris Hightower, Tyler Holquist, Bobby Howe, Holly Leopardi, Morgan Luth, Lonnie Mauck, Alexander Taylor, and Chris Valness. Support from Humboldt State University’s L.W. Schatz Demonstration Tree Farm is gratefully acknowledged.
Cite this paper
Brandon H. Namm,John-Pascal Berrill, (2016) Tanoak (Notholithocarpus densiflorus) Coarse Root Morphology: Prediction Models for Volume and Biomass of Individual Roots. Open Journal of Forestry,06,1-13. doi: 10.4236/ojf.2016.61001
References
- 1. Bingham, I. J., Baddeley, J. A., & Watson, C. A. (2001). Development and Evaluation of Technique for the Rapid Measurement of Cereal Root Systems. HGCA Project No. 257, London: Home Grown Cereals Authority.
- 2. Böhm, W. (1979). Methods of Studying Root Systems. Berlin: Springer.
http://dx.doi.org/10.1007/978-3-642-67282-8 - 3. Coutts, M. P. (1983). Development of Structural Root Systems in Sitka Spruce. Journal of Forestry, 56, 1-16.
http://dx.doi.org/10.1093/forestry/56.1.1 - 4. Coutts, M. P., Nielsen, C. C. N., & Nicoll, B. C. (1999). The Development of Symmetry, Rigidity and Anchorage in Structural Root System of Conifers. Plant and Soil, 217, 1-15.
http://dx.doi.org/10.1023/A:1004578032481 - 5. Danjon, F., & Reubens, B. (2008). Assessing and Analyzing 3D Architecture of Woody Root Systems, a Review of Methods and Applications in Tree and Soil Stability, Resource Acquisition and Allocation. Plant and Soil, 303, 1-34.
http://dx.doi.org/10.1007/s11104-007-9470-7 - 6. Danjon, F., Caplan, J., Fortin, M., & Meredieu, C. (2013). Descendant Root Volume Varies as a Function of Root Type: Estimation of Root Biomass Lost During Uprooting in Pinus pinaster. Frontiers in Plant Science, 4, 402.
http://dx.doi.org/10.3389/fpls.2013.00402 - 7. Danjon, F., Fourcaud, T., & Bert, D. (2005). Root Architecture and Wind-Firmness of Mature Pinus pinaster. New Phytologist, 168, 387-400.
http://dx.doi.org/10.1111/j.1469-8137.2005.01497.x - 8. Drexhage, M., Chauviere, M., Colin, F., & Nielsen, C. C. N. (1999). Development of Structural Root Architecture and Allometry of Quercus petraea. Canadian Journal of Forest Research, 29, 600-608.
http://dx.doi.org/10.1139/x99-027 - 9. Fitter, A. H., Stickland, T. R., Harvey, M. L., & Wilson, G. W. (1991). Architectural Analysis of Plant Root Systems: 2. Influence of Nutrient Supply on Architecture in Contrasting Plant Species. New Phytologist, 118, 375-382.
http://dx.doi.org/10.1111/j.1469-8137.1991.tb00019.x - 10. Kalliokoski, T., Nygren, P., & Sievanen, R. (2008). Coarse Root Architecture of Three Boreal Tree Species Growing in Mixed Stands. Silva Fennica, 42, 189-210.
http://dx.doi.org/10.14214/sf.252 - 11. Kalliokoski, T., Sievanen, R., & Nygren, P. (2010). Tree Roots as Self-Similar Branching Structures: Axis Differentiation and Segment Tapering in Coarse Roots of Three Boreal Forest Tree Species. Trees-Structure and Function, 24, 219-236.
http://dx.doi.org/10.1007/s00468-009-0393-1 - 12. Lavigne, M. B., & Krasowski, M. (2007). Estimating Coarse Root Biomass of Balsam Fir. Canadian Journal of Forest Research, 37, 991-998.
http://dx.doi.org/10.1139/X06-311 - 13. Le Goff, N., & Ottorini, J.-M. (2001). Root Biomass and Biomass Increment in Beech (Fagus sylvatica L.) Stand in North-East France. Annals of Forest Science, 58, 1-13.
http://dx.doi.org/10.1051/forest:2001104 - 14. Littell, R. C., Milliken, G. A., Stroup, W. W., Wolfinger, R. D., & Schabenberger, O. (2006). SAS for Mixed Models (2nd ed.). Cary, NC: SAS Institute Inc.
- 15. Mao, Z., Saint-André, L., Bourrier, F., Stokes, A., & Cordonnier, T. (2015). Modelling and Predicting the Spatial Distribution of Tree Root Density in Heterogeneous Forest Ecosystems. Annals of Botany, 116, 261-277.
http://dx.doi.org/10.1093/aob/mcv092 - 16. Nicoll, B. C., & Ray, D. (1996). Adaptive Growth of Sitka Spruce Root Systems in Response to Wind Action and Site Conditions. Tree Physiology, 16, 891-898.
http://dx.doi.org/10.1093/treephys/16.11-12.891 - 17. Nielsen, C. C. N., & Hanson, J. K. (2006). Root CSA-Root Biomass Prediction Models in Six Tree Species and Improvement of Models by Inclusion of Root Architectural Parameters. Plant and Soil, 280, 339-356.
http://dx.doi.org/10.1007/s11104-005-3503-x - 18. Noordwijk, M., Spek, L. Y., & de Willigen, P. (1994). Proximal Root Diameter as a Predictor of Total Root Size for Fractal Branching Models. Plant and Soil, 164, 107-117.
http://dx.doi.org/10.1007/BF00010116 - 19. Nygren, P., Lu, M., & Ozier-Lafontaine, H. (2009). Effects of Turnover and Internal Variability of Tree Root Systems on Modeling Coarse Root Architecture: Comparing Simulations for Young Populus deltoides with Field Data. Canadian Journal of Forest Research, 39, 97-108.
http://dx.doi.org/10.1139/X08-158 - 20. Oppelt, A. L., Kurth, W., & Godbold, D. L. (2001). Topology, Scaling Relations and Leonardo’s Rule in Root System from African Tree Species. Tree Physiology, 21, 117-128.
http://dx.doi.org/10.1093/treephys/21.2-3.117 - 21. R Development Core Team (2003). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
- 22. Richardson, A. D., & Dohna, H. Z. (2003). Predicting Root Biomass from Branching Patterns of Douglas-Fir Root Systems. Oikos, 100, 96-104.
http://dx.doi.org/10.1034/j.1600-0706.2003.12081.x - 23. Santantonio, D., Hermann, R. K., & Overton, W. S. (1977). Root Biomass Studies in Forest Ecosystems. Pedobiologia, 17, 1-31.
- 24. SAS Institute Inc. (2004). SAS/STAT 9.1 User’s Guide (Vol. 1-7). Cary, NC: SAS Institute Inc.
- 25. Soethe, N., Lehmann, J., & Engels, C. (2007). Root Tapering between Branching Points Should Be Included in Fractal Root System Analysis. Ecological Modelling, 207, 363-366.
http://dx.doi.org/10.1016/j.ecolmodel.2007.05.007 - 26. Stokes, A., & Mattheck, C. (1996). Variation of Wood Strength in Tree Roots. Journal of Experimental Botany, 298, 693-699.
http://dx.doi.org/10.1093/jxb/47.5.693 - 27. Tappeiner, J. C., McDonald, P. M., & Roy, D. F. (1990). Lithocarpus densiflorus (Hook. and Arn.) Rehd. In R. M. Burns, & B. H. Honkala (Tech. Coords.), Silvics of North America: Volume 2. Hardwoods (pp. 827-842). United States Department of Agricultural Handbook 654, Washington DC: SRS Publication.
- 28. Thome, D. M., Zabel, C. J., & Diller, L. V. (1999). Forest Stand Characteristics and Reproduction of Northern Spotted Owls in Managed North-Coastal California Forests. Journal of Wildlife Management, 63, 44-59.
http://dx.doi.org/10.2307/3802486 - 29. Vercambre, G., Pages, L., & Habib, R. (2003). Architectural Analysis and Synthesis of Plum Tree Root Systems in an Orchard Using a Quantitative Modeling Approach. Plant and Soil, 25, 1-11.
http://dx.doi.org/10.1023/A:1022961513239 - 30. Zanetti, C., Vennetier, M., Mériaux, P., & Provansal, M. (2015). Plasticity of Tree Root System Structure in Contrasting Soil Materials and Environmental Conditions. Plant and Soil, 387, 21-35.
http://dx.doi.org/10.1007/s11104-014-2253-z
NOTES
*Corresponding author.









