Open Journal of Forestry
Vol.05 No.05(2015), Article ID:56220,10 pages
10.4236/ojf.2015.55042
Selection Strategy for Chestnut (Castanea sativa Mill.) Families Originating from Contrasting European Populations
Dorothy T. Tchatchoua1,2, Filippos A. Aravanopoulos1
1Laboratory of Forest Genetics and Forest Tree Breeding, Faculty of Agriculture, Forestry and Natural Environment, Aristotle University of Thessaloniki, Thessaloniki, Greece
2Present Address: Department of Agriculture, Animal Husbandry and Derived Products, The Higher Institute of the Sahel (ISS), University of Maroua, Maroua, Cameroon
Email: aravanop@for.auth.gr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2015; accepted 8 May 2015; published 11 May 2015
ABSTRACT
Genetic material originating from contrasting European chestnut (Castanea sativa) populations of Greece, Italy and Spain was evaluated in a common garden test situated in Greece. The aim of the study is to device an appropriate selection strategy by identifying and conserving superior genotypes for current and future use in breeding programs. Breeding material consisted of 143 open- pollinated families growing in a common garden provenance-progeny experimental trial. Growth trait genetic parameters were estimated and response to selection was evaluated using family, within family and combined selection methods. Two models were employed for the estimation of family variance and genetic parameters. The CVA varied between 12.1% and 67% among traits and models, showing an increasing trend with age. Heritability estimates were high; however their variation with age was irregular. Selection of superior families regarding three years of measurement for height, diameter, volume index and number of leaves showed a potential gain of 12% - 25%, 12% - 28%, 33% - 73% and 21% - 49% over the mean of all plants. Genetic gain for volume index was the highest among the traits studied and the joint model used presented a more effective selection strategy. Results indicate that the experimental trial studied presented substantial genetic variation and sufficient genetic gain opportunities for quantitative traits of economic importance. These findings suggest that inferior trees can be rogued from the experimental trial and a seedling seed orchard of Castanea sativa in Greece can be established.
Keywords:
Castanea sativa, Growth Traits, Family Variation, Genetic Parameters, Genetic Gain

1. Introduction
European chestnut (Castanea sativa Mill.), is one of the most important multipurpose broadleaf species in Western Europe and the Mediterranean. The species is widely cultivated for its valuable timber and edible starchy fruits, while it is also used for landscape architecture. In rural areas, chestnut cultivation constitutes an integral part of the economies (Aravanopoulos et al., 2001) . However, the species is considered threatened since it is under direct pressure from a number of environmental and anthropogenic risks. The combination of a higher demand for wood and chestnuts and increased threats, make the selection and conservation of superior genotypes highly impotent. Superior phenotypes can be selected as plus-trees in forest stands and their potential genetic superiority can be established in progeny trials (Zobel & Talbert, 1984) . Response to selection may be predicted on the basis of biostatistical models provided appropriate statistical and genetic parameters are determined from field experimentation (Falconer, 1989) . This approach permits the prediction of the effectiveness of a wide range of various methods of selection, based on different selection criteria. Of particular interest is the “combined family and progeny within family” selection. This method results in a higher genetic gain especially for low heritability traits (Falconer, 1989) which may not be amenable to QTL mapping and MAS selection. Growth traits are often evaluated in breeding programs, since they are important components of plant vigour and biomass production, directly related to wood economic value (Bradshaw & Stettler, 1995) .
In order to study growth traits in C. sativa, a provenance-progeny trial was established in Taxiarchis, Greece based on provenance material that originated from six populations of contrasting environmental conditions across Europe. This trial is part of a network of six similar trials that have been established in Greece, Italy and Spain and involve reciprocal transplantations of provenances. Considerable family variation was already detected at the plant juvenile stage and at the first years after plantation establishment (Pliura & Eriksson, 2002; Fernandez-Lopez et al., 2005; Tchatchoua & Aravanopoulos, 2010) . In addition genetic parameters of growth traits using different models were estimated in another study (Tchatchoua & Aravanopoulos, 2010) . Results indicated that genetic improvement is possible through selection of superior genotypes. The aim of this paper is to use estimates of genetic parameters in order to predict effective selection strategies among open-pollinated families.
2. Materials and Methods
2.1. Description of the Experiment
Genetic material originated from six natural contrasting European chestnut (Castanea sativa) populations of Greece, Italy and Spain (Figure 1). Open-pollinated progenies were raised from 26 randomly selected trees of each population. Collectively the progenies of one parent are referred to as a family. Since the mother was known but the pollen contribution was from a number of trees and given the fact that self-fertilisation in chestnut is limited to non-existent (Papadima et al., 2007) , the progenies are considered half-sibs to each other. Seeds were collected in autumn, sown during the winter 2001, nursery bred during 2001 in Lourizan (NW Spain, at the sea level) and planted at six sites of chestnut breeding zone in March-April 2002. The test site in Greece is located at the University Forest of Taxiarchis-Chalkidiki with altitude 760 m, longitude 23˚18'12"W and latitude 40˚44'35"E. The plantation consisted of 143 open pollinated families in a completely randomized block of 20 replications with single-tree plot and 3 × 3 meters spacing.
2.2. Data Analysis
The following growth traits were measured four years after planting in the field: diameter (basal stem diameter taken with a calliper), height (shoot height measured from the ground to the top of the highest stem or branch
with a measuring rule), volume index (calculated as  and number of leaves (total
and number of leaves (total
number of leaves per individual). Variances of the independent variables [age, block, provenance, and family (provenance)] were tested for homogeneity by using Levene’s test (Sokal & Rohlf, 1981) . An analysis of variance (ANOVA) was carried out using two models presented below and Duncan’s multiple range tests were calculated for each measured traits. The following models were employed:
Figure 1. Geographical location of six contrasting European chestnut populations present in the experimental plantation.
1) Model I (Joint Model)
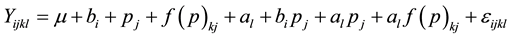
This joint model was employed to test the effect of provenance × age and family × age interactions. The sources of variation taken into consideration were: age, block, provenance, family (provenance), provenance × age and family × age interactions. The model included age, block, provenance and provenance × age interaction as fixed effect and family (provenance) and family × age interaction as random effect.
2) Model II

In model II, analyses were performed to determine the effect of age at measurement. The sources of variation were block, provenance, and family (provenance),
where,
Yijkl = phenotypic observation for the ijklth seedling
μ = the overall mean of the experiment
bi = the fixed effect of the ith block, i = 1,…, 10
pj = the fixed effect of the jth provenance, j = 1,…, 6
f(p)kj = random effect of the kth family within the jth provenance, k =1,…, 9 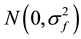
al = the fixed effect of the lth age, l = 1,…, 3
εijkl = the sampling error 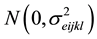
Variance components were estimated by means of the Restricted Maximum Likelihood (REML)/VARCOMP of SPSS software. The derived variance components were used in the computation of additive coefficient of variation (CVA), heritability and response to selection as follows:
Additive coefficients of variation (CVA)

Heritability estimates (Shelbourne, 1992) :
1) family heritability:

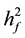 = family heritability
= family heritability
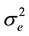 = error variance
= error variance
n = mean number of individuals per family
a = ages
2) within family heritability:
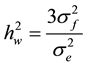
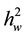 = within family heritability
= within family heritability
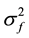 = family variance
= family variance
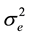 = error variance
= error variance
Response to selection from 10% selection intensity (Zobel & Talbert, 1984) :
1) family selection which involves the choice of entire families on the basis of their phenotypic values:

where,
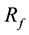 = response to family selection
= response to family selection



2) within family selection where individuals are chosen on the basis of their deviation from the family mean, and family values are not given weight when selections are made:
where,




3) combined selection which is a two stage process, involving selection on families followed by selection of individuals within families.
where, 
3. Results
3.1. Provenance Variation
The analysis of variance of all variables over years (Table 1) shows provenances were highly significant for diameter, height, and volume index, but not significant for the number of leaves. Analysis of variance per year (Table 2) revealed provenance effects that were significant at ages four and six for diameter while no particular trend were observed for the provenance effect with age. Provenance effects differed significantly for height with p ≤ 0.001. Significant effects caused by provenance indicate that most of the genetic variation resides among
Table 1. Variances and p-values for growth traits evaluated in Castanea sativa regarding Model I ANOVA.
Prov.: provenance, Fam. (Prov.): family within provenance, df: degrees of freedom.
Table 2. Variances and p-values for all growth traits evaluated in Castanea sativa regarding Model II ANOVA.
Prov.: provenance, Fam. (Prov.): family within provenance, df: degrees of freedom.
provenances. Regarding the analysis of variance for volume index, the provenance effect decreased at age five and increased at age six (p = 0.039). Provenance effects showed no significant differences at all ages for the number of leaves. The age × provenance was not significant for all the variables measured. The absence of significant interaction variation at the experimental test site for all traits indicated a high correspondence in the different variables with age. The separation of means obtained from the Duncan Multiple Range Test (DMRT), presented the following range: 3.7 - 4.0 for diameter, 95.5 - 119.2 for height, 1229.8 - 1725.0 for volume index and 510.3 - 596.7 for the number of leaves at age six.
3.2. Family Variation
The range values of family means for the variables measured were 2.2 - 5.4 cm for diameter, 56.5 - 170.0 cm for height, 264.6 - 3084.0 cm3 for volume index and 75.0 - 1075.0 for the number of leaves, at all ages. Variation among families was significant for all traits regarding Model I, i.e. the joint Model (Table 1). The respective variance per year (Table 2) revealed significant family effects at age six, while these effects increased with age. The analysis of variance for volume index showed that the family effect had no particular trend with regards to age, being highly significant at age six (p = 0.037). For the number of leaves regarding all ages, family effects were significant at age five (p = 0.029). The age × family interactions was not significant for all the variables measured. The absence of significant interaction variation at the experimental test site for all traits indicated a high correspondence in the different variables with age.
3.3. Additive Coefficient of Variation
The additive coefficients of variation (CVA) values for all traits are presented in Table 3. The CVA varied from 23% (diameter) to 73% (volume index) among traits. The volume index had the highest CVA among traits studied. The additive coefficient of variation was estimated for the traits studied at all ages and accounted for up to 19.3% for diameter, 12.1% for height, 52.6% for volume index and 39.1% for the number of leaves. The CVA for all traits followed an increasing trend with age (Table 4).
Table 3. Additive coefficient of variation (CVA,) heritability and genetic gain for growth traits evaluated in Castanea sativa regarding Model I ANOVA.
σ2f(p): variance component of family (provenance), CVA: coefficient of variation, h2: heritability, Rf: response to family selection, Rw: response to within family selection, Rc: response to combined selection.
Table 4. Additive coefficient of variation, heritability and genetic gain for four growth traits evaluated in Castanea sativa at ages four to six.
σ2f(p): variance component of family (provenance), CVA: coefficient of variation, h2: heritability, Rf: response to family selection, Rw: response to within family selection, Rc: response to combined selection.
3.4. Heritability
The family heritability was high for all the traits regarding Model I, in particular it was 0.76 for diameter, 0.78 for height, 0.72 for volume index and 0.62 for the number of leaves (Table 3). These values affirm the high magnitude of the family variation. The heritability for diameter, height, volume index and number of leaves for age four to six separately are presented in Table 4. Between family heritability was higher than within family heritability and the age trends were parallel for all traits. Regarding diameter and volume index, all heritability values increased as the plants matured. On the other hand, for height and number of leaves, heritability increased until age five and then decreased at age six.
3.5. Predicted Genetic Gain
Estimated genetic gain at 10% selection intensity among families ranged from 14% - 31% for diameter, 15.1% - 35% for height, 41.8% - 87% for volume index and 22.6% - 51% for the number of leaves among the different selection methods in the joint Model. Among the traits studied, the genetic gain for volume index was the highest (Table 3). Hence, family variance has specifically influenced the analysis of genetic gain in the Models employed. Furthermore, the high heritability values that were estimated also contributed to high genetic gains.
Concerning the predicted genetic gain (Table 4), it was highest at age six for all traits. This result shows that combined selection resulted in a higher genetic gain than other methods of selection. Selecting 10% of the best individuals from the best families can lead to an increase in values of diameter by 0.02% - 24%, of height by 0.98% - 34.6%, of volume index by 5.2% - 57.9% and of the number of leaves by 0.0% - 38.8% among the ages of measurement. No consistent trends were observed among all traits with regards to age. In fact, similar trends were noticed between genetic gain values and heritability with increasing age among most traits. Evidently the changes in heritability with age had a corresponding impact on the estimate of genetic gain.
4. Discussion
To aid genetic improvement it is important that superior genotypes are selected, fingerprinted and conserved for future use. Family variation in the provenance-progeny trial of Taxiarchis, Greece indicated that potential genetic improvement is possible through artificial selection. This study evaluated growth trait genetic parameters as an aid for the selection of an optimal breeding strategy for chestnut. The analysis of variance of all variables showed that the factor of provenance to be highly significant. In other provenance-progeny tests of broad leaved species, significant differences attributed to provenance (population) are generally found. For instance, significant differences between Q. robur provenances were found in growth characteristics (Shutz & Badoux, 1979; Kleinschmit & Svolba, 1979; Kleinschmit, 1993; Shutyyaeu, 1999; Jensen, 2000) .
Variation among families was significant for all traits in Model I, while the analysis of variance per year revealed that family effects were significant at age six, increasing with age. Other pertinent studies in Castanea sativa also recorded significant differences among families (Pliura & Erikson, 2002, Fernandez-Lopez et al., 2005) . Strong significant family effects were also encountered for height growth at the juvenile stage of another Fagaceae species, Quercus robur, in a study of open-pollination families in Lithuania (Baliuckas & Pliura, 2003) . Similar family variation was also observed among Betula pendula progenies (Armstrong, 1999) and among B. pendula seed sources from Northern Britain for height growth (Worrell et al., 2000) . Furthermore, congruent results were reported in Fraxinus excelsior where the differences in mean height at age five were found to be statistically significant (Cundall et al., 2003) . Similar results were reported for Prunus avium mean tree height variation among progenies as well (Owe, 2001) . Besides angiosperms, significant family variation for growth was extensively reported in conifers, for example in Picea abies (Skroppa, 1982) , and Pinus contorta spp. latifolia (Xie & Ying, 1996) .
The age × provenance and age × family interactions were not significant for all the variables measured. The absence of significant interaction variation at the experimental test site for all traits indicated a high correspondence in the different variables with age. This is the first time that such analysis has included age as source of variation in Castanea sativa. Similarly, family × year interactions were not significant for all traits measured in a complete diallel performed by crossing Norway spruce grafts of high altitude parents at a low elevation site (Skroppa, 1994) . On the contrary Douglas-fir provenance test showed a significant provenance × age interaction in early selection parameters (Zas et al., 2004) . In this Model I, the data were combined over the three years of measurement to test the effect of the interaction terms among sources of variation. Age × family interactions was statistically not significant indicating high stability across years for all the variables. Based on these results, early selection among families from the test site may be effective. Making selection at early ages is a common practice with the aim of shortening breeding cycles in advanced generation tree improvement programs. Besides accelerating breeding progress, selection at early ages may also offer other advantages such as smaller genetic tests, easier measurement, greater adaptability to changing demands, and quicker delivery of genetic gain to the production population (Lambeth, 1980) .
The CVA for all growth traits followed an increasing trend with age in the C. sativa trial studied. The CVA for height was comparable to that of Pliura & Eriksson, (2002) . However, it was higher compared to the CVA estimates reported by Lauteri et al., (2004) for C. sativa and higher than height CVA estimates reported for other broadleaves species (Baliuckas et al., 1999; 2000) . Family heritability can be high among years and models, while heritability values changed in an irregular way from age four to age six. Family heritability is usually high because it is based on averages estimated with a sample of many progenies. The effects of environmental factors within a test are thus averaged out for the family mean (Zobel & Talbert, 1984) . Heritability estimates were calculated assuming the open-pollinated progenies studied were half-sibs. Any remote possibilities of consanguineous mating, or full-sib mating, might influence heritability estimates. Lauteri et al., (2004) also studied C. sativa heritability on different individuals of the same open pollinated families (i.e. progeny individuals originating from the same mother tree), however using fewer families than this study. They reported higher heritability estimates than the present study. They noted however that only the family and family × treatment components were used in their analysis of variance and the few factors among which total variance was distributed in conjunction to juvenile stage of the plant material (six months old) and the quite uniform environmental conditions (Phytotron experiment) may have led to the higher heritability estimates. Pliura & Eriksson, (2002) also carried out studies on the same open pollinated families. They also estimated higher heritability values than the present study regarding carbon isotope discrimination and height. They attributed their high heritability estimates to the reason explained above which likely resulted in a low environmental variance. Discrepancies in heritability estimates are not unusual and could be attributed to the experimental design, size and composition of the population under study, as well as to the method of data collection (Falconer & Mackay, 1996) . Heritability values that are derived from a single test site as in this report tend to be overestimated (Illingworth, 1978; Ying et al., 1986) . Nevertheless, the estimated heritability values obtained in this study do indicate that the growth traits evaluated are at least moderately heritable. Therefore, they provide evidence that artificial selection may be effective for the improvement of these traits. Heritability estimates showed changes over time which can be attributed to the changes in the external environment with age and to changes in genetic control through gene × environment interaction (Namkoong et al., 1972; Namkoong & Conkle, 1976) . However, no particular trend could be determined in this present study, potentially due to the relatively short measurement period. Elevated heritability values for diameter and height with age were found in Douglas-fir, but at a more advance age of measurement than in this present study (Namkoong et al., 1972; King et al., 1988; Magnussen & Yanchuk, 1994; St. Clair, 1994; Johnson et al., 1997) .
The estimated genetic gain from a 10% selection intensity among families ranged from a low of 12% (diameter, height) to 73% (volume index) among the different selection methods with combined selection having the highest gain. Among the traits studied, the genetic gain for volume index was the highest. Similar results were noticed in the analysis of Tchatchoua & Aravanopoulos, (2010) using models with interaction terms. Hence, family variance has specifically influenced the analysis of genetic gain. Genetic gain estimates for height are comparable to those of Savill et al., (1999) , who estimated a genetic gain of 16% from selecting the best 15% of families obtained at six years from four ash (Fraxinus excelsior) progeny tests. Rink, (1984) predicted genetic gain for height to be up to 25% using family selection strategies in black walnut (Juglans nigra). Higher genetic gain results were obtained in open-pollinated sycamore (Platanus occidentalis) families measured at age seven years (Nebgen & Lowe, 1985) . The estimated high values were perceived to be inflated because members of the open-pollinated families were probably more closely related than half-sibs. The genetic gain for the number of leaves at age four was recorded as zero, since this variable presented zero heritability. Therefore no gain can be accumulated concerning this variable at this age. At age five, combined selection yielded a higher value than family selection. Among all the traits, the highest genetic gain was recorded for volume index and the joint model used resulted in a more efficient selection strategy. Gain can be increased if superior genotypes are vegetatively propagated (Randall & Cooper, 1973; Beineke, 1983) , a possibility that exists for elite mother trees of Greek origin regarding this experimental plantation (Tchatchoua et al., 2014) . This result indicated that the provenance-progeny experimental trial of Taxiarchis has ample amounts of genetic variation in the quantitative traits studied and sufficient gains can be foreseen.
5. Conclusions
The following conclusions can be drawn from this study: 1) Castanea sativa growth traits at the juvenile stage were under strong genetic control; 2) sufficient heritability was recorded to permit selection; 3) combined selection had the highest genetic gain and the joint Model used resulted in a more efficient selection strategy; 4) notable genetic gains can be realized after rouging inferior trees from the experimental plantation and converting the trial to a seedling seed orchard.
A seedling seed orchard could cover immediate needs for improved seeds for wood production. The economic and temporal gains of this option outweigh the alternative of creating a seed orchard as an entirely new effort.
Acknowledgements
This work is part of the Ph.D. thesis of the first author, funded by the Hellenic State Scholarship Foundation (IKY), Greece. Assistance in the field measurements by the Aristotle University Forest Fund is gratefully acknowledged. Special thanks are extended to the Taxiarchis Head Forester Mr. G. Panourgias for providing logistical support.
References
- Aravanopoulos, F. A., Drouzas, A. D., & Alizoti, P. G. (2001). Electrophoretic and Quantitative Variation in Chestnut (Castanea sativa Mill.) in Hellenic Populations in Old-Growth Natural and Coppice Stands. Forest, Snow and Landscape Research, 76, 429-434.
- Armstrong, L. (1999). Provenance Variation in Silver birch (Betula pendula Roth). M.Sc. Thesis, Edinburgh: University of Edinburgh.
- Baliuckas, V., & Pliura, A. (2003). Genetic Variation and Phenotypic Plasticity of Quercus robur Populations and Open-Pollinated Families in Lithuania. Scandinavian Journal of Forest Research, 18, 305-319. http://dx.doi.org/10.1080/02827580310005153
- Baliuckas, V., Ekberg, I., Eriksson, G., & Norell, L. (1999). Genetic Variation among and within Population of Four Swedish Hardwoods Species Assessed in a Nursery Trial. Silvae Genetica, 48, 17-25.
- Baliuckas, V., Largestrom, T., & Eriksson, G. (2000). Within and among Population Variation in Juvenile Growth Rhythm and Growth in Fraxinus excelsior and Prunus avium. Forest Genetics, 7, 193-202.
- Beineke, W. F. (1983). The Genetic Improvement of Black Walnut for Timber Production. In J. Janick (Ed.), Plant Breeding Reviews, AVI Publ., USA 1, 236-266. http://dx.doi.org/10.1007/978-1-4684-8896-8_8
- Bradshaw, H. D., & Settler, R. (1995). Molecular Genetics of Growth and Development of Populus IV. Mapping OTLs with Large Effects on Growth, Form and Phenology Traits in a Forest Tree. Genetics, 139, 963-973.
- Cundall, E. P., Cahalan, C. M., & Connolly, T. (2003). Early Results of Ash (Fraxinus excelsior. L) Provenance Trials at Sites in England and Wales. Forestry, 76, 385-400. http://dx.doi.org/10.1093/forestry/76.4.385
- Falconer, D. S. (1989). Introduction to Quantitative Genetics. New York: Longmann, 428.
- Falconer, D. S., & Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. New York: Longman, 464.
- Fernandez-Lopez, J., Aravanopoulos, F. A., Botta, R., Villani, F., Alizoti, P. A., Cherubini, M., Diaz, R, Mellano, G., Zas, R., & Eriksson, G. (2005). Geographic Variability among Extreme European Wild Chestnut Populations. Acta Horticulturae, 693, 403-411.
- Illingworth, K. (1978) Study of Lodgepole Pine Genotype-Environment Interaction in BC. In: Proceedings International Union of Forestry Research Organizations (IUFRO) Joint Meeting of Working Parties: Douglas-fir provenances, Lodgepole Pine Provenances, Sitkas Spruce Provenances and Abies Provenances (pp. 151-158). Vancouver.
- Jensen, J. S. (2000). Provenance Variation in Phenotypic Traits in Quercus robur and Quercus petraea in Danish Provenance Trails. Scandinavian Journal of Forest Research, 15, 297-308. http://dx.doi.org/10.1080/028275800447922
- Johnson, G. R., Snierzko, R. A., & Mandel, N. I. (1997). Age Trends in Douglas-Fir Genetic Parameters and Implication for Optimum Selection age. Silvae Genetica, 46, 349-358.
- King, J. N., Yeh, F. C., & Heaman, J. G. H. (1988). Selection of Growth and Yield Traits in Controlled Crosses of Coastal Douglas-Fir. Silvae Genetica, 37, 158-164.
- Kleinschmit, J. (1993). Intraspecific Variation of Growth and Adaptive Traits in European Oak Species. Annals of Forest Science, 50, 166s-185s. http://dx.doi.org/10.1051/forest:19930716
- Kleinschmit, J., & Svolba, J. (1979). Possibilities of Genetic Improvement of Quercus robur and Q. petraea. III. Progeny Testing of Selected Seed Trees. Allgemeine Forst Jagdezeitung, 150, 111-120.
- Lambeth, C. C. (1980). Juvenile-Mature Correlations in Pinaceae and Implications for Early Selection. Forest Science, 26, 571-580.
- Lauteri, M., Pliura, A., Monteverdi, M. C., Brugnoli, E., Villani, F., & Eriksson, G. (2004). Genetic Variation in Carbon Isotope Discrimination in Six European Populations of Castanea sativa Mill., Originating from Contrasting Localities. Journal of Evolutional Biology, 17, 1286-1296. http://dx.doi.org/10.1111/j.1420-9101.2004.00765.x
- Magnussen, S., & Yanchuk, A. D. (1994). Selection Age and Risk Finding the Compromise. Silvae Genetica, 49, 25-40.
- Namkoong, G., & Conkle, M. T. (1976). Time Trends in Genetic Control of Height Growth in Ponderosa Pine. Forest Science, 22, 2-12.
- Namkoong, G., Usanis, R. A., & Silen, R. R. (1972). Age-Related Variation in Genetic Control of Height Growth in Douglas-Fir. Theoretical and Applied Genetics, 42, 151-159. http://dx.doi.org/10.1007/BF00280791
- Nebgen, R. J., & Lowe, W. J. (1985). The Efficiency of Early and Indirect Selection in Three Sycamore Genetic Tests. Silvae Genetica, 34, 72-75.
- Owe, M. (2001). Wild Cherry (Prunus avium L.) for Timber Production: Consequences for Early Growth from Selection of Open-Pollinated Single-Tree Progenies in Sweden. Scandinavian Journal of Forest Research, 16, 117-126. http://dx.doi.org/10.1080/028275801300088161
- Papadima, A., Drouzas A. D., & Aravanopoulos, F. A. (2007). Gene Flow in Natural Chestnut (Castanea sativa Mill) Seedling and Coppice Population. Proceedings of the 13th Panhellenic Conference of the Hellenic Forest Science Society, Kastoria, 444-452.
- Pliura, A., & Eriksson, G. (2002). Genetic Variation in Juvenile Height and Biomass of Open-Pollinated Families of Six Castanea sativa Mill. Populations in a 2 × 2 Factorial Temperature × Watering Experiment. Silvae Genetica, 51, 152-160.
- Randall, W. K., & Cooper, D. T. (1973). Predicted Genotypic Gains from Cottonwood Clonal Tests. Silvae Genetica, 22, 165-167.
- Rink, G. (1984). Trends in Genetic Control of Juvenile Black Walnut Height Growth. Forest Science, 30, 821-827.
- Savill, P. S., Spennser, R., Robert, J. E., & Hubert, J. D. (1999). Sixth Year Results from Four Ash (Fraxinus excelsior) Breeding Seedling Orchards. Silvae Genetica, 48, 92-100.
- Shelbourne, C. J. A. (1992). Genetic Gain from Different Kinds of Breeding Populations and Seed or Plant Production Population. South African Forestry Journal, 160, 49-65. http://dx.doi.org/10.1080/00382167.1992.9630411
- Shutyaeu, A. M. (1999). Population Structure of Oak Forests. Lesovedenie, 4, 3-9.
- Shutz, J. P., & Badoux, E. (1979). Yield of Young Oak Stands in Relation to Site Conditions. Mitteilungen Eidgenossische Anstault Forstliche Versuchsweson, 55, 1-177.
- Skroppa, T. (1982). A Critical Evaluation of Methods Available to Estimate the Genotype × Environment Interaction. Studies Forestry Suecia, 166, 3-14.
- Skroppa, T. (1994). Growth Rhythm and Hardiness of Picea abies Progenies of High Altitude Parents from Seed Produced at Low Elevations. Silvae Genetica, 43, 95-100.
- Sokal, R. R., & Rohlf, F. J. (1981). Biometry (p. 859). New York: W.H. Freeman and Co.
- St. Clair, J. B. (1994). Genetic Variation in Tree Structure and Its Relation to Size in Douglas-Fir. 1. Biomass Partitioning, Foliage Efficiency, Stem Form and Wood Density. Canadian Journal of Forest Research, 24, 1226-1235. http://dx.doi.org/10.1139/x94-161
- Tchatchoua, D. T., & Aravanopoulos, F. A. (2010). Evaluation of Selected European Chestnut (Castanea sativa) Provenances II: Intra-Provenance Family Variation. Acta Horticulturae, 866, 215-224.
- Tchatchoua, D. T., Barbas, E., & Aravanopoulos, F. A. (2014). Micropropagation of Elite Genotypes of Castatea sativa (Mill.). Journal of Advances in Biotechnology, 3, 200-209.
- Worrell, R., Cundell, E. P., Malcolm, D. C., & Ennos, R. A. (2000). Variation among Seed Sources of Silver Birch in Scotland. Forestry, 73, 419-435. http://dx.doi.org/10.1093/forestry/73.5.419
- Xie, C. Y., Ying, C. C. (1996). Heritabilities, Age-Age Correlations, and Early Selection in Lodgepole Pine (Pinus contorta spp. Latifolia). Silvae Genetica, 45, 101-110.
- Ying, C. C., Illingworth, K., & Calson, M. (1986). Geographic Variation in Lodgepole Pine and Its Implications for Tree Improvement in British Columbia. In: D. M. Baumcartner et al. (Eds.), Lodgepole Pine: The Species and its Management (pp. 45-53). Pullman: Cooperative Extension Service, Washington State University.
- Zas, R., Merlo, E., Diaz, R., & Fernandez-Lopez, J. (2004). Relative Growth Trend as an Early Selection Parameter in a Douglas-Fir Provenance Test. Forest Science, 50, 518-526.
- Zobel, B. J., & Talbert, J. T. (1984). Applied Forest Tree Improvement (p. 528). New York: Wiley.





